基于属性重要性的贪心算法的改进算法
刘 斌, 倪志伟, 赵 敏
(合肥工业大学管理学院,安徽合肥 230009)
从数据库中发现知识(Knowledge Discovery In Database,简称KDD)或称为数据挖掘(Data Mining,简称 DM)[1]的技术自20世纪80年代末提出以来,得到了广泛重视和迅猛发展。许多数据挖掘算法的模型要求被挖掘的数据必须是离散型的,但是现实中很多的数据是连续型的,所以,必须先对连续型数据进行离散处理。对数据进行离散不仅满足了挖掘算法的需要,还可减少各个属性所对应的数据值的数目,从而提高挖掘系统的挖掘效率以及所得知识的可理解性。
粗糙集理论[2]是一种处理不完备不精确信息的知识获取工具,广泛应用于数据挖掘、知识提取、模式识别、专家预测等多个领域。粗糙集[3,4]在应用中一般要求信息系统中的属性值必须是离散型的表达形式,连续属性的离散化[5-7]是粗糙集数据预处理过程中的一个重要环节。
1 相关研究
S=〈U,R,V,f〉,R=C∪{d}是属性集合,子集C和{d}分别称为条件属性集和决策属性集,U={,…,}是有限的对象集合,即论域。设决策种类的个数为r(d)。属性a的值域Va上的一个断点可以记为(a,c),其中,a∈R;c为实数集。在值域上的任意一个断点集合{(a,c1a),(a,c2a),…,(a,ckaa)}定义了Va上的一个分类Pa,即

因此,任意的P=∪Pa定义了一个新的决策表Sp=〈U,R,Vp,fp〉,fp(xa)=i⇔f(xa)∈[cia,ci+1a],对于 x ∈U,i,j∈{0,…,Ka},即经过离散化之后,原来的信息系统被一个新的信息系统所代替。
布尔逻辑和粗糙集理论相结合的离散化算法[8]是粗糙集理论中的离散化算法在思想上的重大突破,是让其中一个断点或几个断点去区分2个实例的不同的不可分辨关系,此种算法的思想是首先在保持信息系统的不可分辨关系不变的前提下,尽量以最少数目的断点集能够把所有实例间的分辨关系区分开。为了求得最小数目的断点集,改进的贪心算法1每次取重要性最高的断点[9]。断点的重要性是以各列中1的数目来衡量的,1的个数多,则断点的重要性高。当有2列1的个数相同时,把断点所在的列值为1的行的1的数目相加,和值越小,则说明断点重要性越高。
原有的改进的贪心算法描述如下[1,9]:
(1)根据原来的信息系统S构造新的信息系统S*。构造新的信息表 S*算法如下:U*={(xi,xj)∈U ×U|d(xi)≠d(xj)};R*={Pra|a∈C},Pra是属性a的第r个断点[Cra,Cr+1a]。对于任意 Pra,如果[Cra,Cr+1a]⊆[min(a(xi),a(xj)),max(a(xi),a(xj))],则Pra((xi,xj))=1;否则 Pra((xi,xj))=0。
(2)初始化断点集CUT=∅。
(3)选取所有列中1的个数最多的断点加入到CUT中,去掉此断点所在的列和在此断点上值为1的行;当有1个以上的断点的1的个数相同时,把列对应的断点所在的列值为1的对应的行的1的数目相加,取和最小的断点。
(4)如果信息系统S*中的元素不为空,则转第(3)步;否则停止。此时CUT即是得到的断点集。
上面算法中,衡量断点的重要性是以列的1的个数多少作为主要标准的,见表1所列。

表1 信息表(一)
P3a所在的列值为1的行的1的数目相加为(3+3+6+3+2+2)=19;P2b所在的列值为1的行的1的数目相加为(3+6+3+4+1+2)=17,因此可以优先取 P2b。
但是当列中1的数目相等,断点所在的列值为1的行的1的数目相加,和值也相等的情况下,没有提出解决的办法。
2 新的改进方案
为了区分存在上述情况下的断点重要性,首先引入以下概念。
定义1 对每个概念X(样例子集)和不分明关系B,包含于X中的最大可定义集和包含X的最小可定义集,都是根据B确定的,前者称为X的下近似集(记为B-(X)),后者称为X的上近似集(记为B-(X))。
定义2 给定知识表达系统 S=〈U,R,V,f〉,对于每个子集X ⊆U和不分明关系B,X的上近似集和下近似集分别可以由B得基本集定义如下:

其中,U|IND(B)={(X⊆U∧∀x∀y∀b(b(x)=b(y)))}是不可分明关系B对U的划分,也是论域U的B基本集的结合。
定义3 集合BNB(X)=B-(X)B-(X)称为X的B边界;POSB(X)=B-(X)称为X的B正域;NEGB(X)=UB-(X)称为X的B负域。
当在列中1的数目相等,断点所在的列值为1的行的1的数目相加,和值也相等的情况下,改进的贪心算法无法选择较为重要的断点,见表2所列[10]。为了解决此类问题,本文提出了基于属性重要性的贪心算法。

表2 信息表(二)
基于属性重要性的贪心算法的改进算法描述如下:
(1)根据原来的信息系统S构造新的信息系统S*。
(2)初始化断点集CUT=∅。
(3)选取所有列中1的个数最多的断点加入到CUT中,去掉此断点所在的列和在此断点上值为1的行;当有1个以上的断点的1的个数相同时,把列对应的断点所在的列值为1的对应的行的1的数目相加,取和最小的断点;当在列中1的数目相等,断点所在的列值为1的行的1的数目相加,和值也相等的情况下,引入属性重要性概念,根据属性重要程度选择相应属性的断点。判断属性重要性的计算方式如下[1]:

则属性a的重要性为rC(D)-rC{a}。
(4)如果信息系统S*中的元素不为空,则转第(3)步;否则停止。此时 CUT即是得到的断点集。
3 实例及结果
考察表3所列的信息表,选择断点分别为P1a=[0.5,1.2],P2a=[1.2,2.6],P3a=[2.6,3.2],P1b=[0.6,2.3],P2b=[2.3,3.5]。由S构造新的信息表S*,见表4所列。
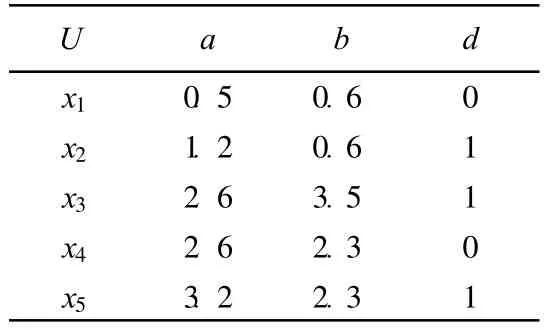
表3 信息表(三)

表4 信息表S*
这时在表4中出现在列中1的数目相等,断点所在的列值为1的行的1的数目相加,和值也相等的情况,就需要引入属性重要性概念并通过该方法确定选择的下一个断点。显然,在表3中,令Q=决策属性集={d},P=条件属性全集={a,b},且

则有:

属性a的重要性为:rC(Q)-rC{a}=1-0.2=0.8;属性b的重要性为:rC(Q)-rC{b}=1-0.6=0.4。属性a的重要性大于属性b,所以优先选择属性a上的断点P2a。
实验结果表明,这种基于属性重要性的贪心算法在分析断点对决策类的区分能力上远远强于贪心算法,在贪心算法无法做出断点判断的情况下,能够有效地区分断点,进而得到最小的断点集。而与文献[9]的改进方法相比,虽然时间复杂度上要大一些,但是考虑的情况比较全面,在前者无法做出识别的情况下,完成断点的判断。
4 结束语
本文针对改进的贪心算法面对断点重要性考虑不全面,提出了一种新的粗糙集离散化的处理方法,即基于属性重要性的贪心算法,先通过分析断点对决策类的区分能力,在区分能力相同的情况下采用属性重要优先算法,逐一将断点加入到断点集中,求得最小断点集,从而完成对信息表的离散化。
[1] 杨善林,倪志伟.机器学习与智能决策支持系统[M].北京:科学出版社,2004:331-332.
[2] Pawlak Z.Rough set[J].International Journal of Computer and Information Sciences,1982,11(5):341-356.
[3] 张文修.粗糙集理论与方法[M].北京:科学出版社,2003:32-36.
[4] Nguyen S H,Nguyen H S.Some efficient algorithms for roug h set methods[C]//Proceedings of the Conference of Information Processing and Management of Uncertainty in Knowledge Based Systems,Granada,Spain,1996:34-37.
[5] 侯利娟,王国胤.粗糙集论中的离散化问题[J].计算机科学,2000,27(12):89-94.
[6] 苗夺谦.Rough Set理论中连续属性的离散化方法[J].自动化学报,2001,27(3):296-302.
[7] 于金龙,李晓红,孙立新.连续属性的整体离散化[J].哈尔滨工业大学学报,2000,32(3):48-53.
[8] 王国胤.Rough集理论与知识获取[M].西安:西安交通大学出版社,2001:99-112.
[9] 宁 伟,赵明清.关于决策表离散化贪心算法的进一步改进[J].计算机工程与应用,2007,43(3):173-178.
[10] 何亚群,胡寿松.粗糙集中连续属性离散化的一种新方法[J].南京航空航天大学学报,2003,35(2):213-215.

