某长江大桥高峰岸锚碇基础边坡稳定性研究①

叶智英，王 朦，梅松华，林孟源，肖拥军

（1.浙江长征职业技术学院，淅江 杭州 310023；2.湖南科技大学，湖南 湘潭 411201；3.中国电建集团中南勘测设计研究院有限公司，湖南 长沙 410014）

目前边坡稳定性分析主要是基于平面应变展开的二维分析，而实际工程中许多边坡地质条件复杂、开挖宽度有限，二维分析得到的结果与实际情况存在较大出入。相比二维分析，三维分析可直观判断边坡破坏性质［1］，得到更准确、更符合实际的分析结果。目前边坡稳定的三维分析广泛采用三维极限平衡法。三维有限元强度折减法与传统三维极限平衡法中“条柱法”的思路完全不同，它能够得出更符合实际情况的计算结果，并且可以得到坡体内应力、变形分布及滑动趋势等信息，对复杂模型更具优势［2－7］。

本文建立某长江大桥高峰岸锚碇基础边坡的三维地质概化模型，对其高峰岸锚碇基础边坡的实际施工过程进行了有限元分析，详细分析了边坡在锚碇施工、运行过程中的应力变形规律，并根据需要针对锚碇基础边坡提出了处理措施，可为大桥两岸边坡的设计方案和工程施工提供科学依据。

1 工程概况

某长江大桥高峰岸锚碇区位于斜坡中部地带，地面分布高程210～240 m，地表土层为块石土，土层厚度0.9～3.2 m。下伏中风化基岩岩体较完整，为沙溪庙组砂岩、泥岩、砂质泥岩，锚碇区基坑开挖后，边坡主要出现在西侧、北侧、东侧及南侧，边坡高度12.0～44.1 m，主要为泥岩和砂岩组成的岩质边坡，上覆少量块石土。在锚碇基坑开挖过程中，开挖最大坡度约73°（垂直于桥轴线方向），因开挖卸荷的影响，基坑上部的覆盖层可能发生滑动破坏；因高峰岸锚碇基础大部分位于中风化泥岩中（见图1），其单轴饱和抗压强度为5.65 MPa，强度较低，而受地形影响，高峰岸基坑开挖边坡较陡，高度大，开挖范围大，且单侧临空，这些因素都可能导致基坑边坡整体滑动。开挖后在基坑东侧形成顺层层面，可能沿岩层层面发生破坏。大桥修建后，在锚碇水平力作用下可能会引起上部泥岩的局部滑动破坏。

图1 高峰岸锚碇基础边坡地质剖面图

2 三维有限元分析

2.1 锚碇基础边坡三维计算模型

三维计算模型依据大桥锚碇基础边坡的工程地质图及锚碇设计方案确定。场地岩层走向一致，基本平行，模型按照岩层的总体产状，将岩层分界面简化为平面。由于锚碇的上部结构对基坑稳定性没有影响，模型中锚碇上部结构完全简化。

计算模型坐标系：平行桥轴线方向为x轴，以指向高峰岸方向为正；垂直桥轴线方向为y轴，以向北偏东向延伸为正；竖直方向为z轴，向上为正。边坡地层分界面以相应的地质剖面图为参照；以锚碇基坑底面中心为原点。

计算模型范围：锚碇基础建模，以锚碇基坑中心为原点，向4个方向各扩展250 m，即计算模型面积为500 m×500 m。模型底面从Z＝0.0 m起取至底面标高。在三维模型概化时，考虑到强风化线埋深较浅，将覆盖层和强风化层合并考虑，覆盖层厚度概化为5 m。高峰岸三维模型共划分单元180 839个、节点64 789个。模型网格划分如图2所示。

图2 高峰岸三维模型网格划分

边界约束条件：地表面自由，无任何约束；底面固定，剩余各面受法向位移约束。

三维计算结果中，以拉应力为正、压应力为负；各图表中未特别说明时，应力单位均为Pa，位移单位均为m。

2.2 边坡岩体力学参数取值

目前Hoek⁃Brown准则是在国际上得到广泛应用的岩体强度准则之一，利用GSI（地质强度指标）法确定岩体的Hoek⁃Brown准则参数快捷、方便，但也有一些缺陷，如GSI的两个参数指标不能定量、GSI值的确定存在一定主观性等［8］。针对GSI方法存在的缺陷，文献［9］提出了基于岩体体积节理数（J v）的岩体结构评分（structure rating，SR）和基于粗糙度、风化和充填评分的结构面表面特征评分（surface condition rating，SC R）两项指标的改进GSI方法。

J v值根据节理统计结果按下式计算［10］：

式中J v为岩体体积节理数，条／m3；S l i（i＝1，2，…，n）为第i组节理每米长度上的条数；S0为每立方米岩体非成组节理条数。

结构面表面特征评分SCR根据下式计算［9］：

式中Rr、Rw、Rf分别为结构面粗糙度、风化度和充填度评分。其评分标准见表1。

表1 SCR评分标准

基于J v获取岩体结构评分SR［9］，分析岩体结构面特征评分，得到SCR，再由SCR确定GSI值，从而确定岩体强度参数。如图3所示。

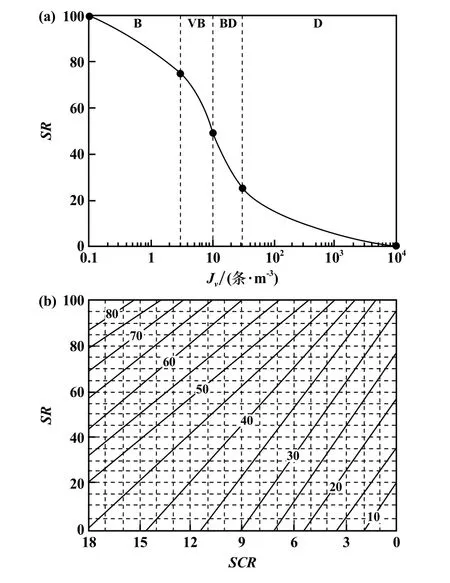
图3 改进GSI方法

图3 （a）中B、VB、BD、D分别表示块状结构、镶嵌结构、碎裂结构／扰动／裂缝以及散体结构；图3（b）中数值10～80为相应的GSI值。综合考虑大桥详勘阶段试验成果，通过工程类比及改进的GSI方法对该区域长江边坡岩土体计算参数综合分析，确定边坡岩体力学参数见表2。

表2 高峰岸边坡稳定分析计算参数取值

2.3 强度折减法原理

强度折减法的原理为：取一折减系数Fs，将边坡岩土体的强度指标c、φ采用式（3）～（4）进行折减，得到一组新的抗剪强度指标c′、φ′，然后在荷载保持不变的条件下采用新的一组抗剪强度指标c′、φ′分析边坡的稳定性；依次类推，不断增加Fs值，折减岩土体强度指标，分析边坡稳定性；直到某一折减强度指标下边坡达到失稳状态，上一级强度指标所对应的折减系数即为边坡的稳定安全系数。

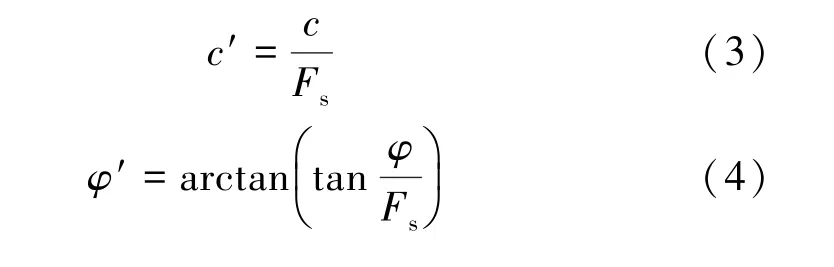
3 模拟结果及分析

分别对自然状态、自然状态＋地震、基坑开挖、运行期、运行期＋地震、运行期＋暴雨共6个工况下的自然状态、基坑开挖、运行期进行应力变形分析，对每种工况计算安全系数。

3.1 边坡变形破坏形式

采用强度折减法，分析不同工况下大桥高峰岸锚碇基础边坡的稳定性，并取地勘报告附平面图中高峰岸垂直于桥轴线32－32地质剖面图，分析其破坏形式及潜在滑裂面剪应变增量分布，计算结果见图4～5。由于其坡度较大，泥岩范围较大，边坡破坏形式除表面覆盖层发生破坏外，在泥岩内部剪应变增量也比较明显。从图4可见，基坑东北侧，靠近模型边界处覆盖层内剪应变增量较大，此处为危险潜在滑裂面。从图5可见，除表层覆盖层外，由于坡度较陡，自然状态在边坡内部产生了近圆弧形式的滑动趋势，潜在滑裂面位于锚碇下方。在开挖和运行工况下，这种滑动趋势更加明显，潜在滑裂面向上几乎贯通到地表，与极限平衡分析结果比较吻合。

图4 整体剪应变分布图

图5 32－32剖面剪应变分布图

3.2 安全系数计算结果

对大桥高峰岸锚碇基础边坡分别进行了二维极限平衡分析、三维强度折减法稳定性分析，两种分析方法计算结果见表3。从表3可以看出，两种方法分析的结果规律比较一致，三维强度折减法计算的安全系数明显高于极限平衡分析法，主要原因是二维模型同地质剖面非常接近；而三维模型考虑整体更为全面，具体计算剖面和二维模型并不完全一致；另外最主要的原因是三维条件下边坡岩土体受三维空间约束作用，岩土体间相互影响而导致其计算结果比极限平衡分析结果大，符合一般规律。

3.3 有限元模拟结果分析

3.3.1 自然状态下的稳定性

高峰岸边坡为缓倾逆向坡，层面稳定性较好，但地形坡度较陡，容易沿覆盖层内部发生局部滑动。在锚碇基坑开挖过程中，受开挖卸荷的影响，基坑上部的覆盖层可能发生滑动破坏；因高峰岸锚碇基础大部分位于中风化泥岩中，基坑可能因岩体强度过低发生整体滑动。大桥修建后，在锚碇水平力作用下可能会引起上部泥岩的整体滑动破坏。

3.3.2 基坑开挖状态下的稳定性

由于高峰岸锚碇结构较复杂，开挖面积较大，应力集中现象相对较轻，开挖后基坑的整体变形趋势是向上向临空面回弹变形，由于自然坡面较大，且仅单侧开挖，基坑开挖后整体位移除向上回弹外，还向开挖卸荷方向变形，从基坑底板变形规律看，随着开挖的进展，变形方向是向上向山体内，最大综合位移符合一般规律。基坑开挖后，垂直桥轴线32－32剖面潜在滑裂面位于基坑后部岩体中，从基坑坡脚处剪出，安全系数为2.37，满足边坡设计要求。

3.3.3 运行期状态下的稳定性

高峰岸基础边坡在运行期间会施加主缆拉力，由于高峰岸锚碇单侧临空，基坑东西两侧的岩体受力较大，塑性区范围会扩大，但影响深度主要在覆盖层内，对整体稳定性影响较小。高峰岸锚碇基础边坡的计算剖面在运行期及运行期＋地震、暴雨的工况下，最低安全系数为2.03，满足边坡设计要求，且有一定安全裕度。

4 结 论

采用改进的GSI方法确定边坡岩体力学参数，基于有限元强度折减法建立某长江大桥高峰岸锚碇基础边坡三维模型，模拟分析施工及运营过程中该大桥高峰岸锚碇基础边坡变形特征及稳定性，得到主要结论如下：

1）采用改进的GSI方法确定边坡岩体力学参数，考虑了开挖方法对岩体扰动的影响，其分析结果更符合工程实际。

2）三维有限元分析法可直观显示边坡破坏形式和位置，便于定性判断边坡破坏特征。由于三维条件下边坡岩土体受三维空间约束作用，岩土体间相互影响而导致其计算结果较极限平衡分析结果偏大，但符合一般规律。

3）该长江大桥高峰岸边坡在基坑开挖、锚碇填筑、桥梁运行阶段各工况条件下，基础边坡稳定性均可满足设计要求。