基于EEMD和小波阈值法的爆破振动信号预处理研究①

李启月，王宏伟，王靖博，曾海登，郑 静，张建秋

（1.中南大学 资源与安全工程学院，湖南 长沙 410083；2.中交一公局第五工程有限公司，新疆 哈密 839000）

爆破振动信号分析一直是矿业、岩土等工程界的研究热点，而实际采集到的信号往往受监测环境、地质条件等因素影响掺杂了大量噪声；同时系统低频性能的不稳定性、放大器随温度变化产生的零点漂移等因素导致振动波形偏离基线中心的现象（即趋势项）。二者导致信号失真，使时域中的相关分析或频谱特性分析产生很大的误差，甚至使低频谱完全失真［1－2］。

常用的爆破振动信号去噪方法主要包括小波类方法［3－4］、经验模态分解类方法（EMD去噪［5］、EEMD去噪［6］）以及两者联合的EMD⁃小波阈值法［7］。小波阈值法以其出色的时频局部化性质和多分辨率特点在非平稳随机信号的滤波消噪处理中备受青睐，但存在小波基选择困难的缺点；经验模态分解（empirical mode decomposition，EMD）自适应地将信号分解为一系列从高频到低频排列的固有模态函数（intrinsic mode function，IMF），但直接滤除高频分量的去噪方法过于粗糙，容易丢失真实信息；EMD⁃小波阈值法有效结合了两者优点，但仍存在EMD模态混叠的问题。而现行的趋势项去除方法中［8－10］，最小二乘法因需预设趋势项类型而使用困难；小波阈值法对基函数选择和分解深度的确定要求过于严格，导致效果欠佳。目前不乏单独针对爆破振动信号的消噪或趋势项去除的研究，但处理尚有局限性，同时涵盖两者的预处理方法鲜有报道。

本文将集合经验模态分解（EEMD）和小波阈值法结合起来，利用皮尔森相关系数结合频谱特性去除趋势项，同时辅以自相关函数特性进行消噪处理，建立了一个便捷、有效的爆破振动信号预处理方法，对于准确提取爆破振动信号时频特征具有重要意义。

1 爆破振动信号预处理方法

1.1 基于相关系数的EEMD趋势项去除方法

1.1.1 EEMD原理

EMD分解过程中所谓的模态混叠现象，表现为一个IMF分量包含了特征尺度相差较大的信号或者相似尺度信号分布在不同IMF分量中。这将冲淡IMF的物理意义，进而带来一系列误差。为此，文献［11］提出了集合经验模态分解（ensemble empirical mode decomposition，EEMD）作为EMD的改进算法。其改进原理是在原始信号中加入一组有限幅值的白噪声，EMD算法产生的原始信号中不同尺度的成分自动投射到由白噪声建立的合适的参考尺度上，运用总体平均的方式获得最终的IMF。在足够多组试验下，白噪声对结果的影响可以减弱甚至抵消。其中，添加白噪声的幅值系数k和总体试验次数由前人经验与自身试验来确定［6］。

EEMD分解步骤如下：

1）在原信号x（t）中添加高斯白噪声和ωi（t）。

式中i为添加次数；x i（t）为添加噪声后的信号。

2）将每个添加噪声后的信号x i（t）进行EMD分解，获得相应的IMF值，记为c ij（t），余项n i（t），其中i＝1，2，…，J，为分解尺度。

3）将每次获得的IMF进行总体平均，得到真实分量c j（t）。

1.1.2 趋势项去除方法

仅把EEMD分解的余项作为趋势项去除是不恰当的，而得到的各IMF分量中哪些作为趋势项的有效组成部分尚无统一的判别准则。这里引入皮尔森互相关系数R和IMF频率f结合的方法，互相关系数表达式如下：

式中R（i）为互相关系数；T为信号长度。

互相关系数描述了两个信号之间的相关程度，理想情况下高频噪声分量和低频趋势项分量与真实信号的互相关系数为0。但是原信号包含了噪声分量和趋势项分量，并受未能完全抵消的白噪声影响，分解出的干扰分量接近于0。根据前人经验和反复试验，取互相关系数R低于0.1的IMF分量作为高频含噪分量和低频趋势项分量的预选［12］。同时考虑到爆破测振仪低频性能的不稳定性，去除预选的低频趋势项IMF中频率f低于频率响应范围的分量，来完成趋势项的处理。

1.2 基于自相关特性的EEMD⁃小波阈值法去噪

1.2.1 小波阈值法

小波阈值法消噪的本质是信号的滤波。通过小波变换对信号不同频率成分进行分解，得到信号的小波分解系数，进而对各层系数中大于或小于某设定阈值系数分别处理，就可以过滤噪声信号。然后对处理过的小波系数进行小波逆变换重构去噪后的信号［13］。通过反复试验，选取基于Stein的无偏风险估计原理确定阈值系数，以软阈值函数进行处理，小波基为db5，分解层数6，效果较好。软阈值函数表达式为：

式中η（ω，λ）为处理后的系数；ω为分解后的小波系数；λ为确定的阈值系数。

1.2.2 EEMD⁃小波阈值法去噪

EEMD方法自适应将信号分解为一系列从高频到低频依次排列的IMF，由此可构造不同频带的滤波器。对于含噪分量难以分辨的问题，借助自相关函数特性，对上述预选的高频含噪IMF分量进行再次筛选，进而对含噪分量进行小波阈值去噪，最大程度保留真实信息。

自相关函数描述了同一个时域随机信号在不同时刻处采样值之间的相互关联程度，其函数表达式为：

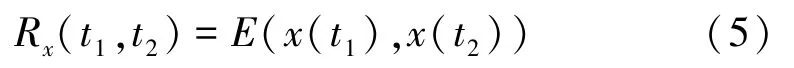
式中t1，t2表示不同的时刻；x（t1），x（t2）表示随机过程x（t）在相应时刻的采样值。

对于理想的高斯白噪声，其自相关函数具有零点取得最大值、其余点为0的特点。

1.3 预处理方法

预处理方法首先是将采集信号进行EEMD分解，然后利用皮尔森互相关系数进行含噪IMF分量和趋势项IMF分量的预选，进而借助频带特点和自相关函数特性进行判断，完成趋势项去除和小波阈值去噪，有效保留信号真实信息，提高频谱分析精度。具体流程如图1所示。

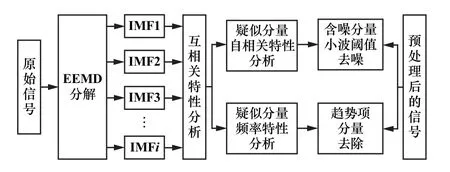
图1 信号预处理流程

2 实例分析及效果评价

选取实测的爆破振动垂向信号，利用上述方法完成趋势项去除和去噪的滤波预处理，并对信号重构效果进行评价。测试条件为：总药量4 400 kg，单段最大药量140 kg，爆心距70 m。

2.1 EEMD分解

设置白噪声标准差0.05，集成次数为100，分解得到11个IMF分量和1个剩余分量，结果如图2所示。从图2可以看出，EEMD方法分解出的IMF分量，有效地改善了端点效应和模态混叠的影响。

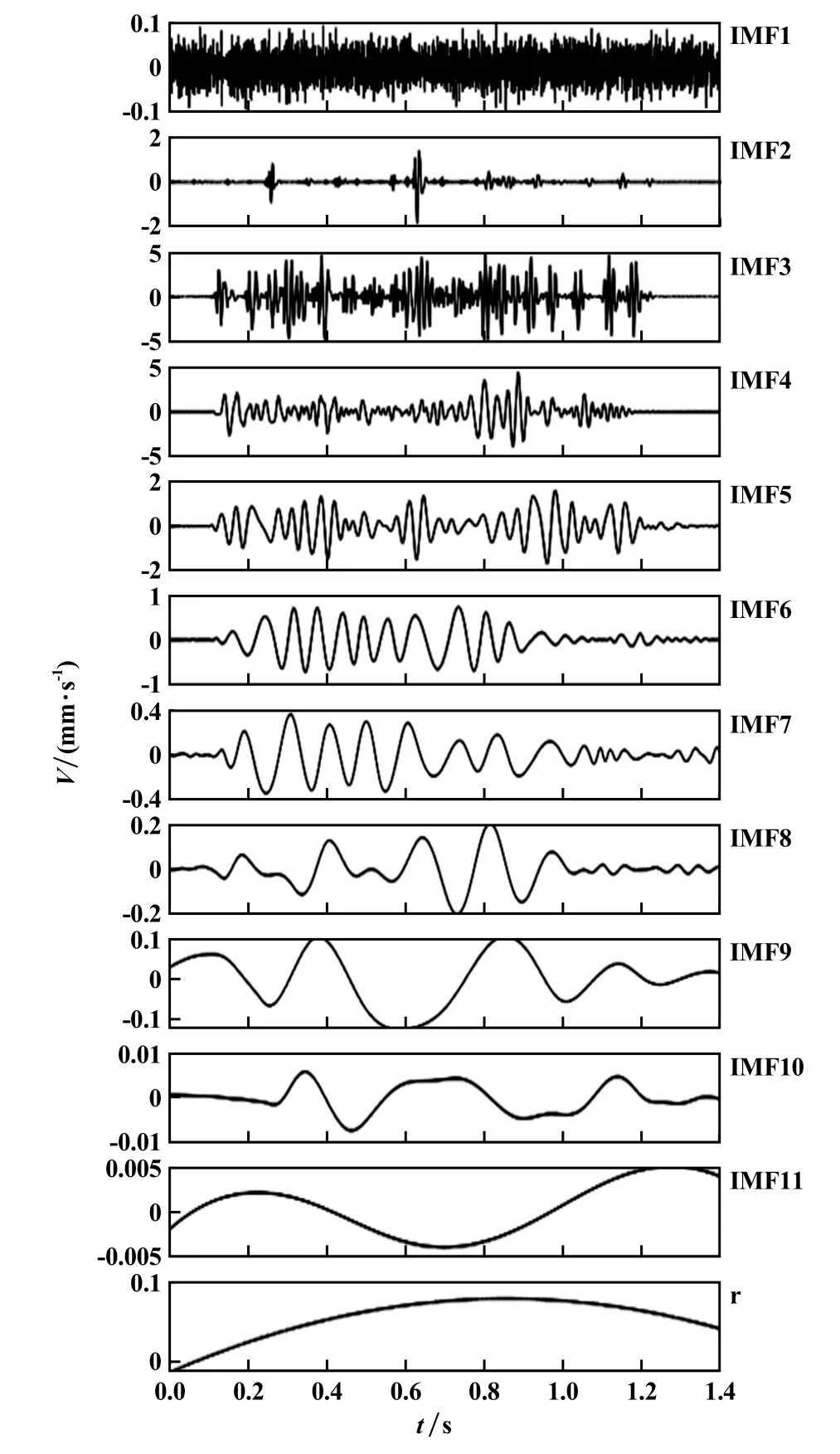
图2 EEMD分解结果

2.2 信号预处理

2.2.1 趋势项去除

针对原始爆破振动信号EEMD分解结果，求取各分量与原信号的互相关系数，结果如表1所示。从表1可以看出：IMF1、IMF2、IMF9、IMF10、IMF11、r分量的互相关系数较小，初步认定为含噪分量和趋势项分量。进而对高阶疑似趋势项分量进行频谱分析，结果如图3所示。由图3可知，IMF9、IMF10、IMF11、r分量频带较窄，集中于0～5 Hz低频段，主频均低于爆破测振仪的有效监测范围，表明IMF9及以后的分量可能是爆破振动信号固有的，也可能是由别的情况引起的，反映了信号的零漂或变化趋势。上述分量引起了趋势项的产生。作为对比，IMF8分量明显频带较宽，主频在有效监测范围内。因此，需将IMF9及以后分量去除。

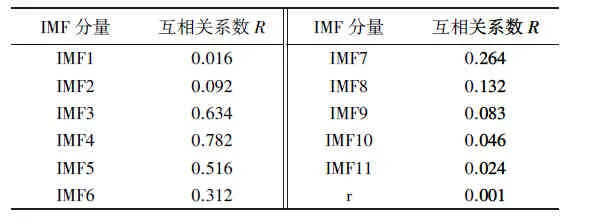
表1 互相关系数对应表

图3 疑似趋势项分量频谱图

2.2.2 信号去噪

针对互相关系数较小的疑似含噪分量IMF1、IMF2进行自相关特性分析，结果如图4所示。从图4可以看出，IMF1分量的自相关函数在零点处取最大值，其他时延处的自相关系数均接近于0，符合噪声的特点，同时考虑到其与原信号的互相关系数接近于0，认定为高频噪声序列，对于几乎不包含真实信息的噪声IMF1分量直接去除；而IMF2分量的自相关系数在零点取得极大值，但其余时延处并不完全符合噪声特性，且与原信号的互相关系数接近含噪序列初选的阈值，因而含噪分量IMF2包含了一定真实信息，对其进行小波阈值消噪处理。

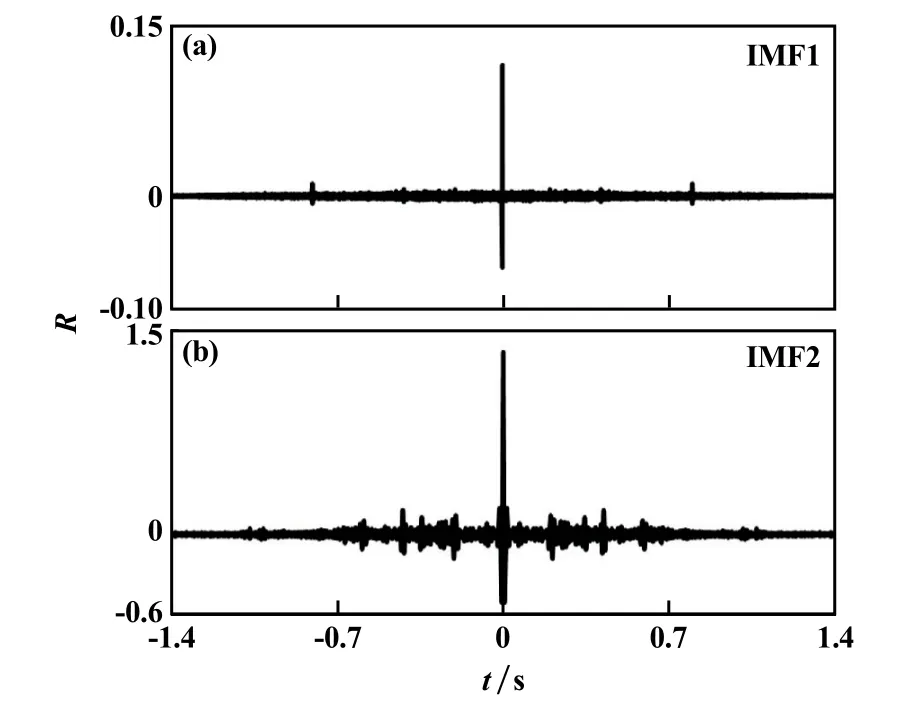
图4 疑似含噪分量自相关函数

2.3 波形重构

完成趋势项去除及消噪后，剩余分量重构回预处理后的信号，原始波形与重构波形如图5所示，原始信号与预处理后信号的频谱如图6所示。从图5可以看出，原信号波形受趋势项和噪声影响偏离基线中央，0.8 s后基本失真，预处理后的信号波形重新回到基线中央，同时曲线更加光滑，保留了波形真实信息。由图6可知，原信号频谱与预处理后频谱走势基本相同，原信号0～5 Hz低频段幅值突高的现象消失，说明趋势项引起的低频响应问题得到较好的解决；85～125 Hz频段内幅值明显降低，受噪声导致幅值拉高的影响，经预处理后消失，而集中于5～85 Hz、135～140 Hz频段的爆破振动信号分量没有明显变化，表明预处理方法消除噪声干扰外，并不会影响到爆破振动信号有效能量分布。这对于准确提取爆破振动信号时频特征具有重要意义。

图5 预处理前后信号波形

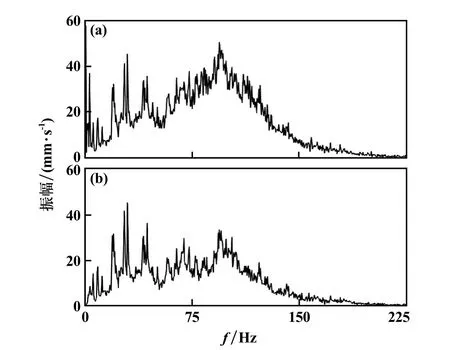
图6 预处理前后信号频谱

2.4 滤波效果对比

信噪比（SNR）反映了信号平均功率与噪声平均功率的比值关系，广泛应用于降噪效果评价，信噪比越高，表明去噪效果越好。其计算公式为：

式中x t为原信号；X t为处理后的信号；T为信号长度。

将信噪比（SNR）和处理前后信号的互相关系数（R）作为滤波效果量化指标，通过单纯的EEMD方法和小波阈值预处理，与本文预处理效果作对比，结果如表2所示。从表2可以看出，本文预处理方法信噪比最高，EEMD方法次之，小波阈值法的最小；本文预处理方法信噪比最高，小波阈值法次之，EEMD方法的最低，说明EEMD方法直接去噪过于粗略，容易丢失真实信息，而小波阈值法去噪效果不如其他两者。综上，借助相关性分析，本文提出的结合EEMD和小波阈值法优点的预处理方法滤波效果优于其他2种方法。

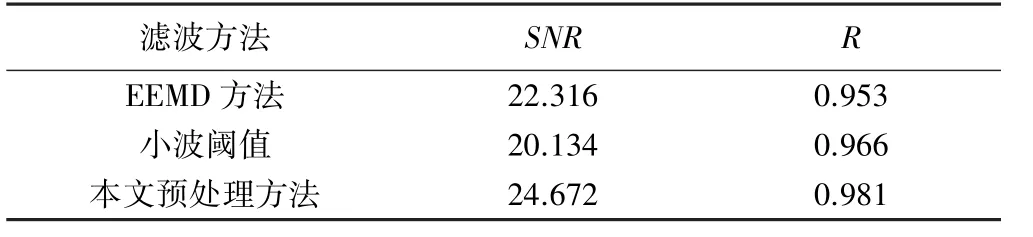
表2 滤波效果对比

3 结 论

为了消除爆破振动信号受噪声以及趋势项的影响，借助相关性分析，引入了一种基于集合经验模态分解（EEMD）和小波阈值法的预处理滤波方法。经过实例验证，得出结论如下：

1）结合了EEMD和小波阈值法优点的预处理滤波方法涵盖了爆破振动信号趋势项去除和消噪两方面，为趋势项分量的判别做了新的探讨，信噪比和互相关系数都比单一EEMD和小波阈值法更高，保留了更多的真实信息。

2）对比预处理前后信号波形和频谱特性，证实本文方法可以有效消除趋势项影响带来的零漂和低频响应问题，去除噪声的同时并不会干扰信号真实能量分布，保留了真实信息，提高信号频谱分析精度，对准确提取爆破振动信号时频特征具有重要意义。