一种新的夜间单图像去雾方法

段镖, 李靖, 陈怀民, 茹懿, 张泽

(1.西北工业大学 自动化学院, 陕西 西安 710072; 2.西北工业大学 机电学院, 陕西 西安 710072)

近年来雾霾天气增多,图像去雾成为图像处理的研究热点。雾霾使得观测图像对比度降低,造成物体的像模糊不清,影响观测结果。在图像处理的另一些应用领域中,一张清晰的图像是各种图像处理算法能够有效发挥作用的先决条件。如图像导航,需要对场景的特征进行识别,而雾霾造成图像对比度的降低,场景特征“隐没”于雾中,造成导航算法失效。因而图像去雾方法通常可作为其他图像算法的预处理步骤,用以增加各种图像观测系统在雾霾天气下的适用性。

图像去雾方法主要分为两类——基于图像增强的第一类方法与基于大气物理成像模型的第二类方法。目前以He Kaiming的黑暗通道优先[1]为代表的第二类去雾方法[1-5]受到了较为广泛的认可,这些算法主要用来解决昼间图像的去雾问题。它们通过对雾霾天气下的成像过程进行建模,以实现无雾图像的最优估计[6]。从本质上而言,通过大气物理成像模型求解无雾图像的是一个病态问题。因其仅含一个方程而包含无雾图像J,大气光值A,透射率t3个未知数。因而其求解过程需要依赖各种先验假设。其基本流程是,利用各种假设,在带雾图像I中,对大气光值A、透射率图t进行估计后,再对去雾图像J进行求解来实现图像去雾。

夜晚图像去雾是图像去雾研究的一个重要分支,夜晚图像去雾有着与昼间图像去雾不同的特点。其一,夜晚去雾不存在全局统一的大气光值夜间图像去雾相较于昼间图像去雾更为复杂。其二,在雾霾天气条件下,雾霾粒子对光的散射作用使得人造光源附近产生明显的“光晕”[7],且人造光源难以像昼间大气光是“灰白色”的[8],因此直接利用光源的颜色来近似估计局部的光照条件容易引起图像的颜色偏移。文献[8]假定夜间大气光值为暗通道图中最亮像素点的像素值,并引入了颜色迁移来抑制因去雾而引起的图像偏移问题,该种方法取得了一定的去雾效果,但是由于需要1幅参考图像来实现颜色迁移,因此其对不同光照条件下的适应性较差。Zhang等人估计光强度并增强它以获得照明平衡的结果,并引入了额外的估计入射光的颜色特性后的颜色校正步骤。最后他们先使用暗通道消除雾霾,然后估算点状环境光。但其容易造成某一颜色通道上的对比度过度增强。Li等人的Schechner和Karpel水下图像模型[9]。 他们假设雾霾图像由图像光晕层和薄雾层叠加而成。首先通过对光晕层进行分离削弱图像的光晕效应,进一步地,假设夜间局部区域的大气光值为局部区域内最亮像素点的像素值,然后再用该点处薄雾层与局部区域的大气光值之比的暗通道运算结果来估计该点处的透射率,并最终从薄雾层中反解出无雾图像。这种方法虽然在一定条件下能够取得较好的去雾效果,但是在图像光晕较强且人造光源单色特性明显的情况下,去雾图像容易产生明显的颜色偏移现象。

受到Li等人通过层分离抑制图像光晕效应的启发,本文假设图像由“光照层”及“反射层”叠加而成,并通过级联滤波的方式将带雾图像的“光照层”与“反射层”进行分离,这样就能在一定程度上抑制人造光源对图像颜色的影响,从而抑制颜色偏移现象。进一步地,本文通过光照层来估计局部的光照情况与透射率,利用反射层来反解出无雾图像。实验结果表明,本文算法取得了较好的去雾效果。

1 构造算法介绍

昼间雾霾图像的成像模型如(1)式所示

I(x)=J(x)t(x)+A(1-t(x))

(1)

式中：x代表图像中的一个像素点；I(x)为带雾图像I中x点处的像素值；J(x)为未经大气衰减的清晰图像J在x点处的像素值,对于去雾算法而言；J代表无雾图像；A代表在图像中的全局大气光值,该值在昼间通常被认为是常量,其代表了太阳光在云层中的散射程度,云层越厚,太阳光在穿透云层时,被散射的能量越多,大气光值越小[10-11]。雾气和云相似,其主要成分是水汽。大气光在到达物体表面后,经物体表面反射,再穿透雾气层,最终到达成像面[12]。透射率t(x)的大小就代表了雾气层的厚度,在物距相同的情况下,雾气越厚,透射率越小。昼间雾霾图像成像假定了大气光是昼间存在的唯一光源,其忽略了各种非自然光源的影响[13]。在昼间,J(x)t(x)项代表了物体表面反射的大气光能量,A(1-t(x))项代表了雾气散射大气光后,被成像设备捕获的光能量。

在夜间的雾霾天气下,情况有所不同。由于月光、星光等相较于太阳光很弱,其能够到达物体表面的能量很少,可以忽略不计,因而夜间不存在全局统一的大气光值[14]。夜间物体表面的反射光主要来自于物体附近的人造光源,不同的人造光源的光谱特性不同,人造光源亦难以像太阳一样明亮,因而各个光源对单个物体的影响难以保持某个光源绝对占优的状况[15]。对于物体而言,其表面的反射情况相对固定,光源对物体成像的影响取决于光源的光强及光源与物体的距离。光源越强,距离物体越近,物体表面的反射光能量来自于该光源的占比越大。更为一般的情况下,物体介于多个人造光源之间,此时物体距离各个光源的距离难以通过像素距离来准确估计[16]。因而通过寻找光源来估计每一像素点处的光照情况存在着先天的不足。

对于单个像素点而言,其像素值可看成是由来自物体表面的反射光能量以及由所有光源发出的光经空气中的雾霾粒子散射后到达成像面的散射光能量的和,如图1所示。因此,夜间大气物理成像模型可由(2)式表示

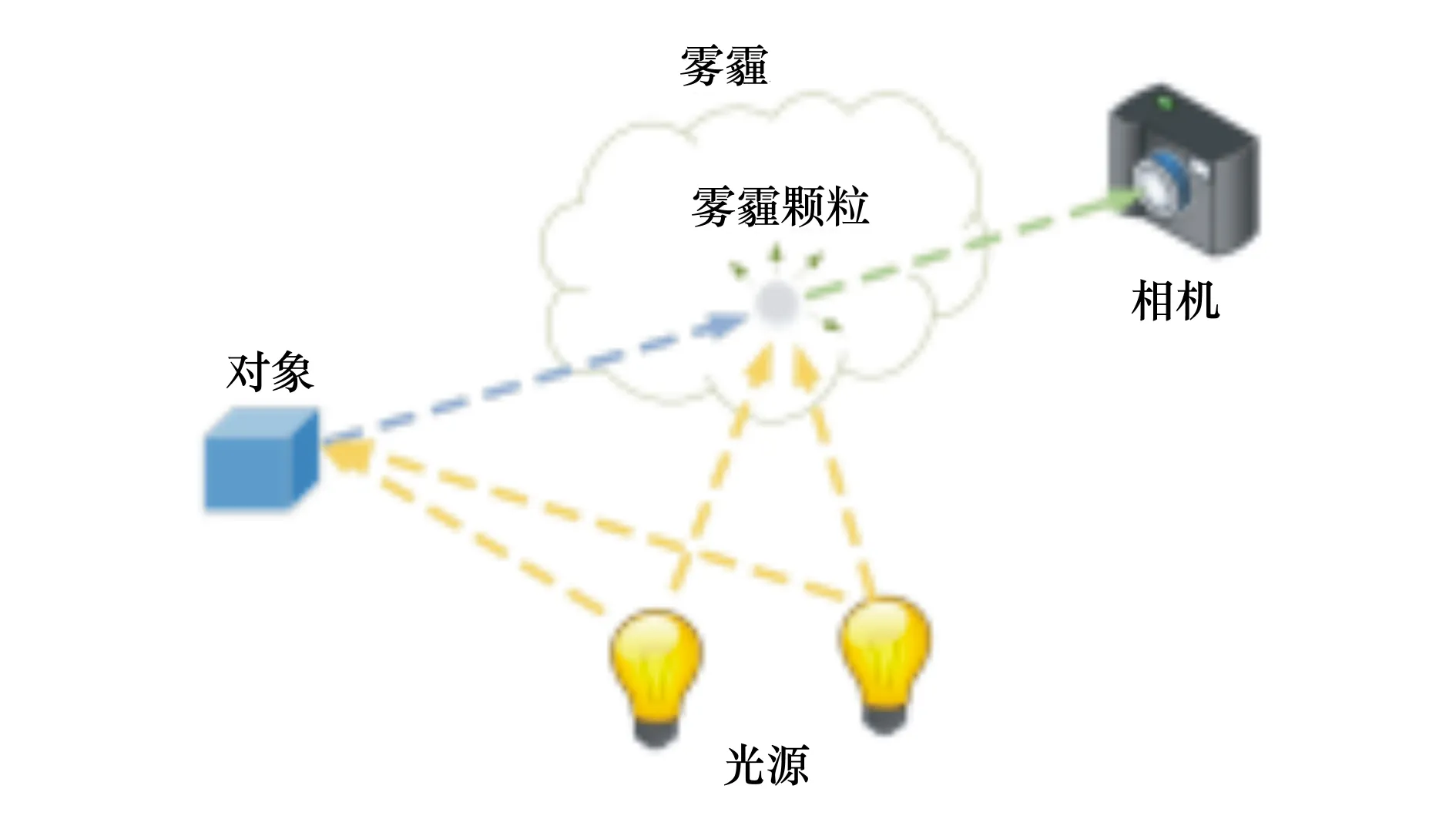
图1 夜间雾霾条件下成像过程示意图

I(x)=J(x)t(x)+L(x)(1-t(x))

(2)

式中：L(x)表示在x点处的光照值,其代表了所有光源在该像素点处的散射光能量,I,t的含义同(1)式相同；J则代表了所有光源发出的光被物表面反射的光能量总和。

求解(2)式最直接的做法是,设法先对L(x)t(x)进行估计,然后利用公式(2)求解J(x),L(x)的估计方法将在本文的第三部分详细讨论。关于透射率t(x)的估计方法,暗原色先验法提供了一种目前认可度较高的求解思路,其中1幅图像I在像素点x处的暗通道Idark(x)定义如下

(3)

暗通道运算的本质是一个在图像局部区域Ω(x)内的2次最小化运算,其中第一次最小化运算,在像素点x处的(r,g,b)三通道中完成;第二次最小化运算,在窗口直径为r的方形区域内完成。

暗通道运算可以对昼间雾图像的透射率进行较为准确估计。在昼间,由于大气光A为全局一致的。暗原色先验假设Idark(x)→0,则A(1-t(x))≫J(x)t(x),故Idark(x)→A(1-t(x)),对大气光A进行适当估计后,则可对x处的图像透射率t(x)进行估计。在夜间,Idark(x)→0,L(x)并非全局一致的,因而不能够保证L(x)(1-t(x))≫J(x)t(x),故Idark(x)→L(x)(1-t(x))并非在全局范围内成立。因此,需要对t(x)的估计方法作出适当改进。

2 本文方法

通过(2)式可以看出,夜间有雾图像可以由J(x)t(x)及L(x)(1-t(x))叠加而成。因此可以假设,夜间有雾图像由两图像层叠加而成。J(x)t(x)代表的图像层,本文称为“反射层”,本文用R表示;L(x)(1-t(x))代表的图像层,本文称之为“光照层”,本文用H表示。则(2)式可重写为

(4)

图像去雾的实现过程,可视作在有雾图像I中,分离出反射层R与光照层H,再对t(x)进行适当估计后,从“反射层”中反解出J的过程。本文算法的示意图如图2所示。

图2 本文算法的示意图

对于一个像素点而言,其像素值代表的光能量来自于图像反射层和光照层两部分。但从本质上来说,所有的光能量都来自于各种光源。图像反射层中代表的光能量,是光源发出的光,经过物体反射与大气散射后最终被成像系统捕获的那部分光能量。而图像光照层中的光,是光源发出的光直接被大气散射后,进入成像系统中的光能量。对于1幅图像中的一个已知点x,其透射率t(x)的大小不变,该点处的光照大小H(x)与光源的光强及远近有关——光源越亮且像素点距离光源越近,光照H(x)越大,反之则越小。光照层的这种特性,使得对它的分离能够用图像的空间滤波来实现。

导引滤波是一种优秀的图像线性空间滤波器,其输入图像I同滤波输出图像Q有如下映射关系[17]

Q=guidedfilter(I,G,r,ε)

(5)

式中：G为导引图像,r为滤波窗口半径；ε为正则化系数。导引滤波假设导引图像G与滤波输出Q图像在局部窗口内满足线性模型

Qi=akGi+bk,∀i∈ωk

(6)

式中：Q表示滤波输出图像,i表示图像中第k个局部窗口ωk中的一个像素点；G表示导引图像,(ak,bk)表示局部窗口ωk中的线性常系数。对(5)式两端同取梯度运算,则Q=akI。该式表明,导引滤波保证了滤波输出图像与导引图像在局部区域内的梯度相似性。同时,文献[18]假设在局部区域内,一个像素点在滤波输出图像上的像素值等于该点在输入图像I上的像素值减去该点处的噪声值,即满足

Qi=Ii-ni

(7)

式中：Q为滤波输出图像,I为滤波输入图像,n为噪声。通过最小化代价函数

(8)

(9)

(10)

图3 光照层分离流程示意图

分离光照层的具体步骤如下:首先,对带雾图像I进行初次导引滤波,其中导引图为其本身。窗口半径r1窗口半径,正则化系数ε1取相对较大的值,本文取r1=30,ε2=1×10-5。由于I(x)=R(x)+H(x)≥H(x),因此,得到初次的滤波输出Q1后,对其像素点的取值进行约束,由此得到粗光照层Hc,其定义如下

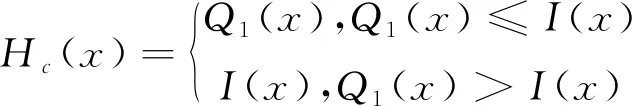
(11)

然后,对粗光照层Hc进行第二次导引滤波,其导引图为第一次导引滤波的输出图像Q1。第一次导引滤波由于添加了约束条件,致使粗光照层中仍然含有部分的反射光信息。而直接使用滤波输出Q1又不能满足I(x)=R(x)+H(x)≥H(x)条件。因此需要进行第二次导引滤波。导引滤波的滤波输出图像同导引图像具有相似的局部梯度,利用这种性质,将Q1作为第二次滤波的导引图像,其输出则能够作为精细光照层估计结果,该图像层用Hp表示。此次滤波窗口半径r2窗口半径,正则化系数ε2取相对较小的值,本文取r2=10,ε2=1×10-5。

最后,在获得光照层后,通过矩阵减法,则能够获得图像反射层的估计R′,如(12)式所示

R′=I-δ·Hp

(12)

式中：δ为常数,其使分离出的反射层R中含有较少的光照层成分,以避免去雾图像整体偏暗,本文取δ=0.95。

在获得图像光照层的精确估计后,接下来需要对雾霾图像的透射率图进行估计。在此之前,首先需要对图像的光照情况进行估计。由于H(x)=L(x)(1-t(x)),因此,可利用光照层的精确估计Hp,对光照情况L(x)进行估计。不同于昼间,夜间光源往往呈现出一定的单色性,因而可用一个像素点处{r,g,b}通道上的最大值来代替该点处的光照值,且在同一局部区域内,光照情况是趋于一致的。故对光照的估计可由(13)式给出

(13)

结合公式(4),可得到透射率的粗估计公式

(14)

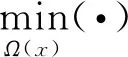
为了避免出现过小的透射率值,需要对tc(x)进行限定,最终的透射率估计由(15)式给出

t′(x)=max(tp(x),0.2)

(15)

利用公式(4),即可求得夜晚去雾图像的估计图像

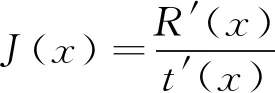
(16)

3 实验结果

本文的实验结果来自于1台拥有Intel(R) Core(TM) CPU i5-6200内核的PC机,处理器主频为2.30 GHz,实验结果在 MATLAB 2011b平台下得出。 实验图像部分来自于互联网,另外一些来自于参考文献[1-3,7]中的demo。本文算法主要与Tarel的方法[3]、Fattal的方法[2]、He的方法[1]、Li的方法比较,并比较了不同夜间光照条件下的3组图像去雾效果。所有对比方法的代码均可以在其作者的主页中找到。其中Tarel的方法[3]、Fattal的方法[2]、He的方法[1]均是在昼间大气物理模型的基础上提出的,Li的方法主要针对于夜间去雾。图4至7均为夜间去雾效果对比,其中图4至图6的子图a)～f)分别为：夜间雾图像、Fattal算法的去雾结果、Tarel算法的去雾结果、He算法的去雾结果、Li算法的去雾结果以及本文算法的去雾结果。

在夜间光源偏亮的情况下,如图4c)、4d)所示,Tarel和He的方法容易使图像的颜色朝向光源方向偏移。而在光源颜色接近白光且较暗的情况下,如图5b)、5d)及图6b)、6d)所示,Tarel和He的方法去雾效果较好。而Fattal的算法容易造成颜色失真,如图4b)及图5b)所示。在图7c)中,Tarel的结果过于接近夜间霾图像本身。

图4 夜间去雾效果对比场景1 图5 夜间去雾效果对比场景2

图6 夜间去雾效果对比场景3 图7 夜间去雾效果对比场景4

Li的算法能够明显提升图像的对比度,但其容易造成噪声的明显放大问题,如图4e)与图7e)中的红色矩形框所示。本文算法能够较为明显抑制光源颜色对图像颜色的影响,使夜间图像中的物体颜色更接近其本身的颜色,其噪声放大现象不明显,综合比较,本文的夜间去雾效果在各种光照情况下下均能够取得较好的效果。

4 结 论

去雾算法目前将研究重点放在白天图像除雾上面,并取得了令人满意的去雾效果。而夜间雾霾图像由于不存在全局统一的大气光值,造成夜间霾图像模型求解过程较为复杂。直接利用昼间去雾算法来实现夜间去雾效果较差。夜间去雾的关键在于如何避免去雾过程中引起的颜色偏移现象。现有算法多通过色彩校正抑制上述现象,但其效果也难以尽如人意。本文通过2层级联的导引滤波,将夜间雾霾图像光照层与反射层分离开来。去除光照层后,光源对物体颜色的影响减小,因而颜色偏移现象也能够得到有效的抑制,且夜间雾霾图像的反射层中较多的保留了物体本身的色彩信息,这样利用反射层来反解无雾图像,能够更加接近真实无雾场景下采集的图像。实验结果表明,本文算法在多场景下均能够取得较好的去雾效果。本文算法获得的夜间去雾图像在光源点附近会产生轻微的亮度下降,这将是未来的研究工作之一。