基于改进最小路的低压配电系统可靠性评估

毛澍，闫志彬，闫涛，王金宇，刘伟，谈军，王晓楠，康健，张丽

(1. 国家能源局电力可靠性管理和工程质量监督中心，北京 100031；2. 国网宁夏电力有限公司，宁夏 银川 750001；3. 中国电力科学研究院有限公司，北京 100192；4. 国家电网有限公司，北京 100031)

作为配电系统的最后一环，低压配电系统连接着公用配电变压器和用户，担负着向用户直接供应电能和分配电能的重要任务[1]。西方发达国家的供电可靠性主要采用面向终端用户的评估评价方式，如国际范围内最具权威的IEEE 1366供电系统可靠性指标标准[2]，其统计到用户电能表，不分电压等级，每个计费点为一个统计单位，故其评估评价结果能真实地反映系统实际可靠性水平,然而，国内供电可靠性评估评价仍主要集中于中高压配电系统，尚未延伸至低压配电系统，且鲜有针对低压系统可靠性评估的相关研究，急需提出一种适用于低压系统的可靠性评估方法[3]。

低压配电系统具有 “点多面广分层多” 等特点，其网络拓扑的梳理难度较大，故难以搭建起可靠性评估的物理模型。针对该问题，部分学者提出基于统计数据的低压配电系统可靠性评估方法[4-9]。文献[4]提出了一种基于概率统计的低压用户供电可靠性评估方法，通过建立系统分区模型和抽取用户停电信息，结合概率统计理论来实现低压配电系统可靠性指标的快速计算。文献[5]提出了一种基于监测点数据的配电系统可靠性评估方法，首先根据测量精度要求设定低电压可靠性监测点，然后基于监测点收集到的运行数据来计算可靠性指标。文献[6]提出了一种基于大数据分析的城市低压配电系统运行可靠性评估算法，该方法以大数据为基础，通过设计综合性评估指标，结合转供容量等参数值，实现了城市低压电网的可靠性评估。文献[7-8]首先分析了低压配电系统用户供电可靠性评估的重要性，然后分别构建了低压配电系统的可靠性评估方法和可靠性预测方法，为低压配电系统的可靠性管理工作提供借鉴作用。文献[9]提出了基于人工神经网络的可靠性评估方法，根据历史可靠性指标和基础数据，评估低压配电系统的可靠性指标。上述方法虽然实现了低压配电系统的可靠性评估，但其评估准确性过于依赖历史统计数据，且短期历史数据难以反映可靠性的真实水平，且难以用于分析网络结构和元件参数对可靠性的影响。

国家能源局于2018年开展低压用户供电可靠性管理试点工作，探索开展低压用户供电可靠性管理研究和实践，梳理了华东地区试点区域的低压网络拓扑关系，为可靠性的解析评估创造了有力条件。试点工作发现，低压配电系统主要为“总箱-分箱-表箱”的多级配电结构，要求配置三段保护，包含较多的低压断路器,然而，低压断路器普遍存在未短路时因操作故障导致的误动作和短路时保护失效导致的拒动作，最终引发不同类型的停电事故[10];因此，为准确评估低压配电系统可靠性水平，本文提出了一种基于改进最小路的低压配电系统可靠性评估方法，能充分考虑低压断路器拒动和误动两种故障模式，实际算例分析证明了方法的合理性和准确性。

1 拒动误动对低压配电系统的故障影响分析

低压配电系统故障，临近故障点的上级断路器跳闸，隔离故障支路，防止故障蔓延至相邻支路，这种保护机制能最大限度地减小停电范围，降低故障影响[11],因此，断路器是否能正确动作直接决定着故障影响范围，故不应忽略其拒动误动对系统可靠性的影响[12-13]。以图1所示系统为例，分析拒动误动对低压配电系统的故障影响。

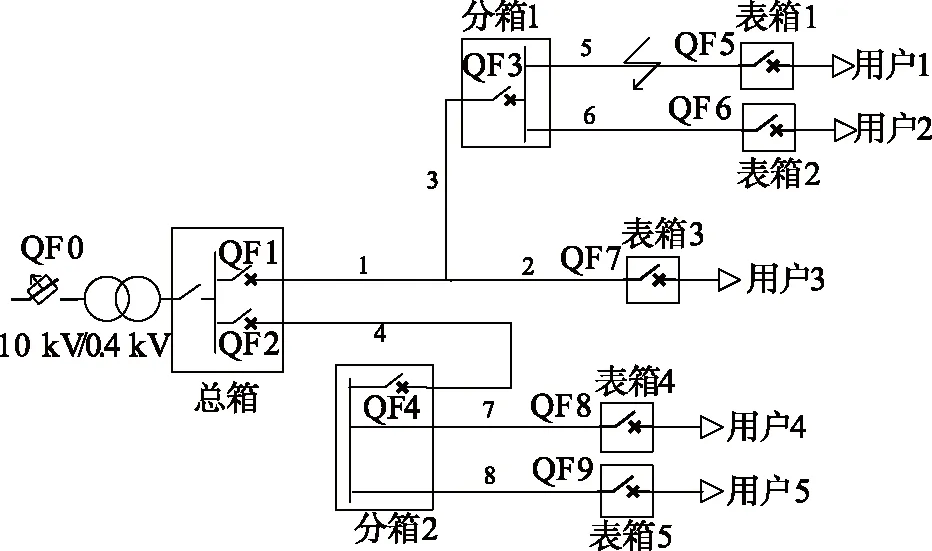
图1 低压配电系统示例

首先，分析因保护失效导致拒动的故障影响。图1中系统的低压线路5发生故障，断路器QF3跳闸，用户1和2停电。若QF3保护失效，发生拒动，则QF1跳闸，用户1至3停电。若QF1也拒动，则配变的跌落保险QF0跳开，用户1至5全部停电，直至故障修复；因此，由于拒动会扩大故障停电范围，故需将拒动甚至多重拒动纳入可靠性分析;然后，分析因操作失误导致误动的故障影响，仍以图1为例，断路器QF3发生误动，则分箱1所带的用户1和用户2停电，直至故障恢复,因此，由于误动会导致系统停电，故需将误动纳入可靠性分析。综上，为保证低压配电系统可靠性评估的准确性，需充分考虑断路器拒动误动两种故障模式，本文基于改进最小路法提出一种能考虑拒动误动的可靠性解析评估方法。

2 基于改进最小路的配电系统可靠性评估方法

最小路法是辐射状中压配电系统可靠性评估的常用方法[14-16]，算法思路如下：首先根据系统网络拓扑，寻找电源点到负荷点间的最短供电路径，即最小路，然后分析系统元件与最小路之间的关系，最终实现可靠性指标的解析分析;然而，传统最小路法并未考虑断路器拒动误动，需改进传统最小路法，故提出了一种基于改进最小路的可靠性解析评估方法，计算流程如图2所示。

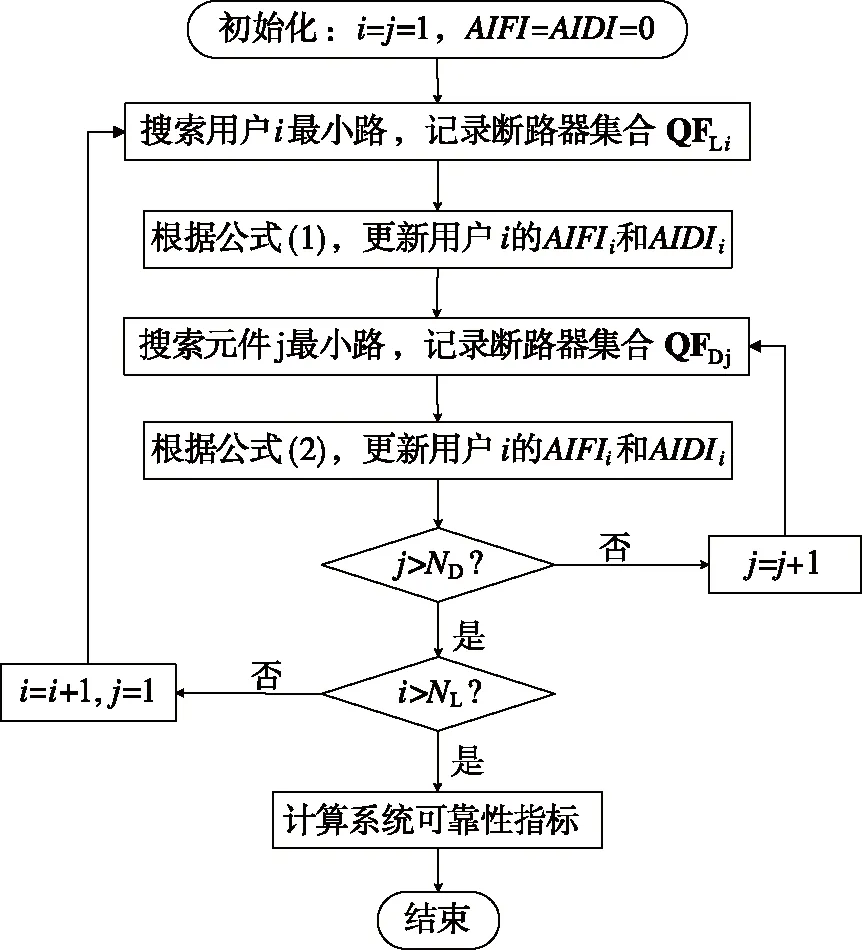
图2 计算流程

详细步骤如下：

步骤1,初始化。设置用户计数器i和元件计数器j，且i=j=1，分别设置系统所有用户年平均停电次数(AIFI)和年平均停电时间(AIDI)，且AIFI=AIDI=0。

步骤2，根据系统网络拓扑，采用深度优先搜索算法[17]，搜索配电变压器到用户i的最小路，记录最小路所包含的断路器集合QFLi。

步骤3，更新用户i的可靠性指标AIFIi和AIDIi，更新方程为

(1)

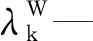
MTTRk—断路器k的平均修复时间，h/a。

步骤4,采用深度优先搜索算法，搜索配电变压器到元件j的最小路，记录最小路所包含的断路器集合QFDj，需要注意的是断路器的最小路不包含自身。

步骤5，更新用户i的可靠性指标AIFIi和AIDIi，更新方程为

(2)

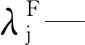
yk(x)—控制变量，其中，当断路器k∈QFLi，则yk(x)=1，否则yk(x)=x；

pk—断路器k的保护失效率。

步骤6，判断j是否大于系统总元件数ND，是则跳转到步骤7，否则j=j+1，并跳转到步骤4。

步骤7，判断i是否大于系统总用户数NL，是则跳转到步骤8，否则i=i+1且j=1，并跳转到步骤2。

步骤8，计算系统可靠性指标，系统平均停电频率(SAIFI)和系统平均停电时间(SAIDI)的计算公式参考中压配电系统的指标计算公式[18]：

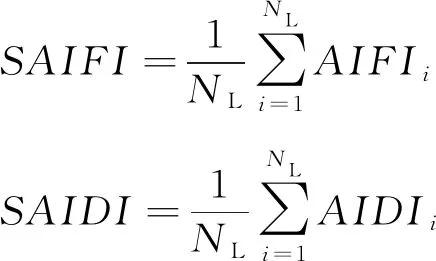
(3)

3 算例分析

算例系统相关数据采集于华东地区供电服务指挥系统，系统包含22个低压用户，36个断路器，29条低压电缆线路，网络结构如图3所示。配变及以上的等效故障率为0.015次/a，等效平均修复时间为8 h，断路器参数见表1，电缆线路参数见表2。

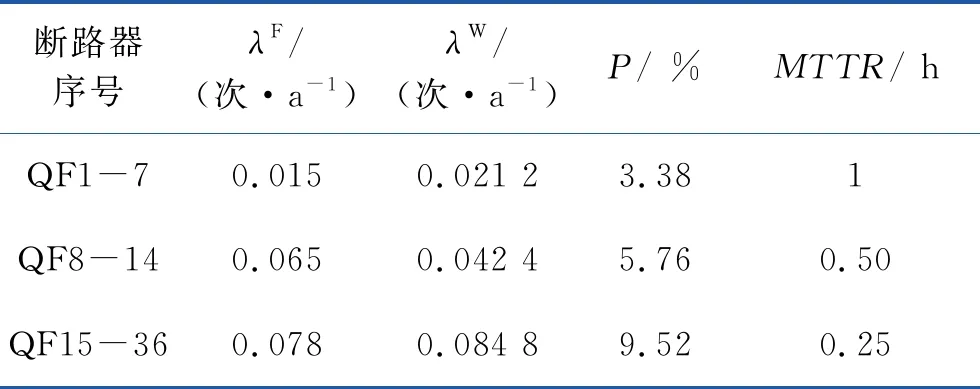
表1 断路器参数

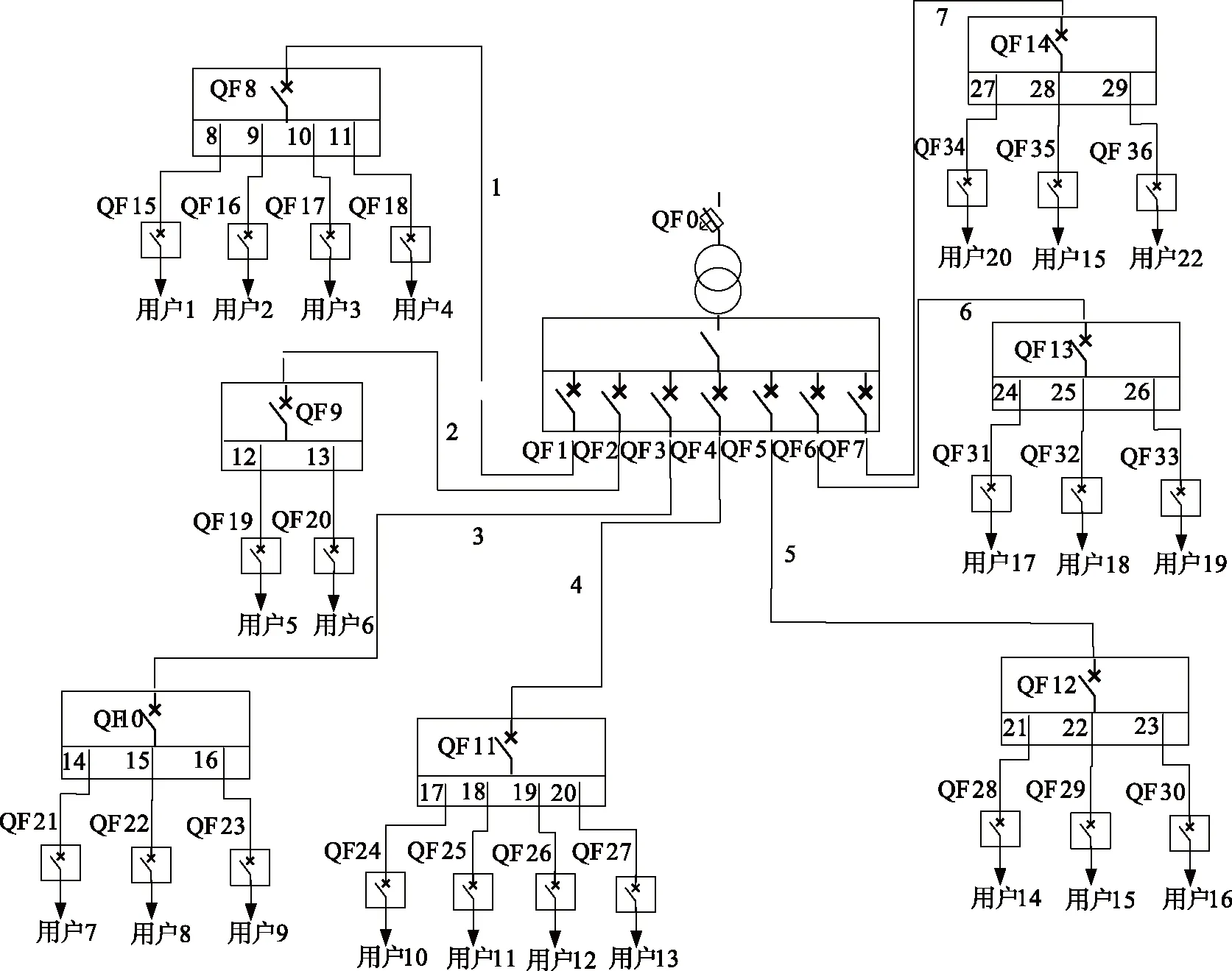
图3 算例系统网络结构

表2 电缆线路参数

3.1 计及低压配网拓扑结构的供电可靠性分析

目前，大部分供电公司仅实现了中压网络拓扑的可靠性分析，获得了中压节点的可靠性指标，但对于低压系统则采用中压节点等效方法进行简化处理，其指标值等同于所属中压节点。为准确评估系统可靠性，本文方法考虑了低压配网拓扑结构，本节将对比分析中压等效法和本文方法的可靠性评估结果，如表3所示，用户可靠性指标如图4所示。

表3 两种评估方法的系统可靠性指标

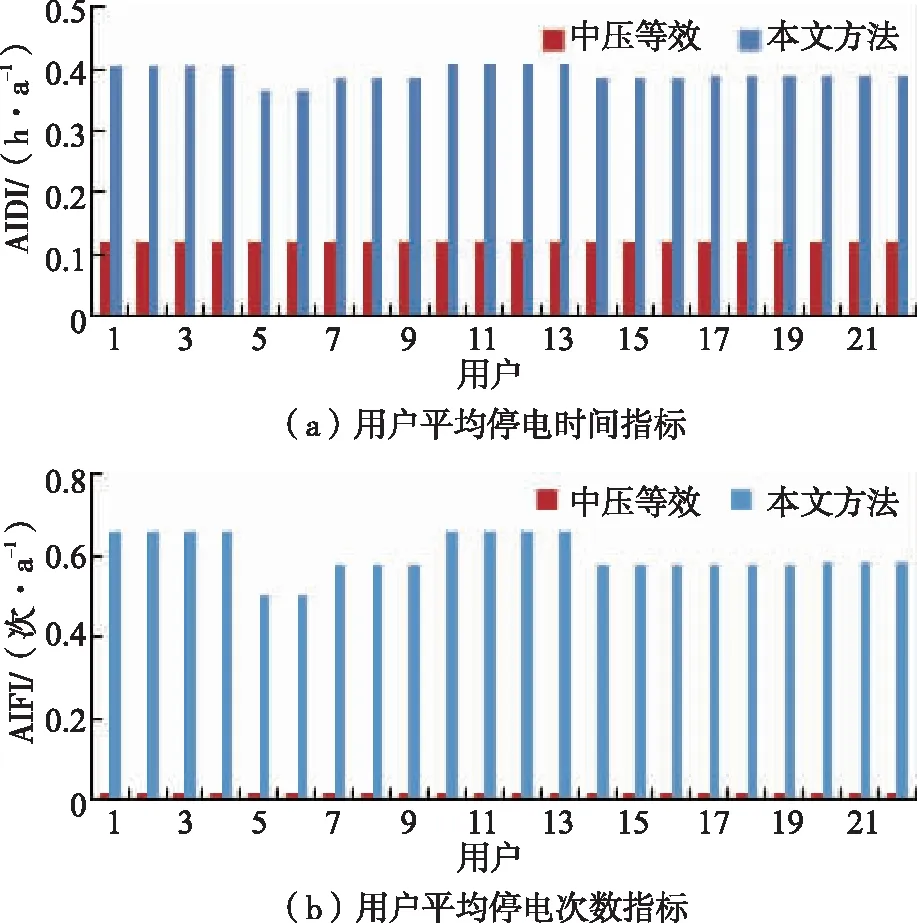
图4 两种评估方法的用户可靠性指标

根据表3可知，相比于中压等效法，本文方法的SAIFI从0.015次/a增加至0.603次/a，增长了39.2倍，SAIDI从0.120 h/a增加至0.392 h/a，增长了2.3倍。两种评估方法的可靠性指标差异巨大，本文方法考虑了低压配网拓扑结构，虽然增加了评估的复杂性，但较能真实地反映低压配电系统的可靠性水平。

根据图4可知，中压等效法的用户AIFI和AIDI完全一致，而本文方法的用户AIFI和AIDI则存在一定的差异，说明中压等效法无法反映出低压网络拓扑和设备故障特性对用户可靠性水平的影响，故其评估结果也无法准确反映用户的真实可靠性水平，不利于可靠性薄弱环节的分析改善。本文方法考虑了低压拓扑结构和设备故障特性，所得的指标也反映出用户可靠性水平的差异性，具有一定的优势。

3.2 拒动误动对低压配电系统供电可靠性的影响

目前，电力系统可靠性评估大部分假设低压断路器能100%正确动作，忽略了断路器操作故障和保护失效的两种故障模式，故两种故障模式对低压配电系统可靠性指标的影响设置以下四种情形：

情形1，不考虑操作故障和保护失效；

情形2，考虑操作故障，但不考虑保护失效；

情形3，考虑保护失效，但不考虑操作故障；

情形4，同时考虑保护失效和操作故障。

采用本文方法分别计算其系统可靠性指标，如表4所示。

表4 四种情形下的系统可靠性指标

根据表4可知，情形2的SAIFI和SAIDI比情形1分别增长了1.336%和0.923%，情形3则比情形1分别增长了32.962%和19.692%，情形4则为34.298%和20.615%。情形2-4的可靠性指标均高于情形1，说明考虑了断路器的操作故障或保护失效后，系统可靠性指标有所降低，即忽略两种故障模式的可靠性指标偏高。此外，根据公式(1)和公式(2)，所有断路器的操作故障率和保护失效率与用户的AIFI和AIDI均呈线性正相关，考虑拒动误动前两参数相当于0，而考虑后两参数相当于从0增至算例给定数值，故必然导致SAIFI和SAIDI的上升。情形3指标的增幅远大于情形2，说明相比于操作故障，保护失效给算例系统的SAIFI和SAIDI带来了更大的增幅，故更换保护失效率较低的断路器给系统可靠性水平带来的提升效果将更明显，故为有效改善算例系统的可靠性，可优先更换保护失效率低的断路器。

3.3 计及低压供电可靠性的断路器设备优选

电网的规划设计通常以供电可靠性为首要目标，并将建设改造费用作为约束条件。假设算例系统计划投资1万元对电缆分接箱内的断路器(QF8-14)进行升级更换以最大程度地提升系统可靠性水平。现某厂家可提供一批全新的电缆分接箱断路器，其故障率为0.043，保护失效率为3.82%，操作故障率为0.031，单价为1580元/台，考虑到1万元仅可购买6台断路器，故此次升级改造无法全部更换，需剩余1台断路器。分别计算剩余QF8-14中的任意一台断路器的系统可靠性指标，计算结果如表5所示。

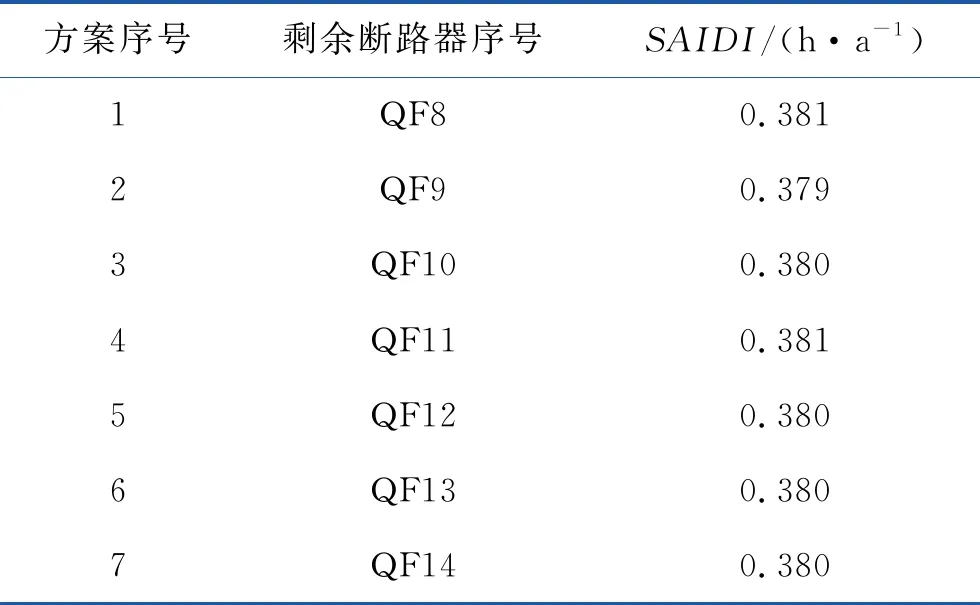
表5 剩余不同断路器的系统可靠性指标

从表5可以看出，方案2的SAIDI最低，为0.379 h/a，方案1和方案4的SAIDI最高，为0.381 h/a，其余方案为0.380 h/a，说明此次升级改造应采用方案2，能最大程度地提升可靠性。此外，根据表1可知，算例系统中QF8-14的参数完全一致，故7种方案的提升效果亦可通过观察来验证，即通过比较断路器拒动误动影响的用户数量来判断需要改造的对象，QF9影响用户5-6，QF8和QF11分别影响用户15-18和用户24-27，显然此算例系统中QF9对于系统可靠性的影响最小，侧面论证了本文方法的合理性。因此，本文方法可用于低压配电系统的升级改造，具有一定的工程应用价值。

4 结论

本文提出了一种基于改进最小路的低压配电系统可靠性解析评估方法，首先基于深度优先搜索算法搜索出给定低压拓扑结构下的元件最小路和用户最小路，然后通过分析元件和用户最小路之间的逻辑关系以及系统元件故障特性，解析计算出系统可靠性指标，结论如下：

(1)相比于中压等效法，本文方法进一步考虑了低压网络结构和拒动误动的情况，能更好地反映低压网络拓扑和设备故障特性对可靠性水平的影响，提升了系统可靠性评估的真实性和终端用户可靠性指标的差异性。

(2)建立了设备故障特性与可靠性指标间的数学函数关系，考虑了系统故障后断路器能正常断开故障点、断路器拒动无法断开故障点和操作故障引发断路器误动的三种故障情景，实现了具有“多级保护”结构的低压配电系统可靠性的量化分析。

(3)通过分析计及低压供电可靠性的断路器设备优选，证明了本文方法的工程应用价值。