基于材料基因工程的AP/Al/HTPB推进剂单轴拉伸性能及脱湿过程计算

董 戈，张 炜，周 星，邓 蕾

(国防科技大学 空天科学学院，湖南 长沙 410072)

引 言

固体推进剂药柱不仅是固体火箭的能量来源，也是固体火箭发动机的承力构件之一。目前，推进剂力学性能是影响推进剂配方设计的重要因素，定应变速率拉伸(单轴拉伸)下推进剂的力学行为是评估推进剂力学性能的常用方法。

传统推进剂配方设计及力学性能调节通常采用“经验+试验型”研发方法[1]，即根据经验设计推进剂配方，再经历样品制备、力学性能测试、配方调整、再测试等多轮试验，最终达到指标要求，但该方法的成本很高。

近年来，基于数值模拟的推进剂力学性能细观计算逐渐成为研究热点[2]，并在计算模型及参数取值等方面积累了一些成果。许进升等[3]基于应力松弛实验数据，通过“唯象法”回归，获得了prony形式的基体黏弹性模量表达式；职世君等[4]基于Hooke-Jeeves方法，结合推进剂单轴拉伸数据获得填料-基体界面模型参数。然而现有计算模型仍多依赖于实验数据，且未与实际推进剂配方建立联系，不具备对不同体系、不同配方推进剂的普适性。因此，既未充分发挥数值模拟方法的优势，也不能很好地指导推进剂力学性能调节。

“材料基因工程”[5]作为含能材料研发的一种新模式，旨在实现材料研发模式从“经验型”向“理论预测型和设计型”的转变。张炜[6]提出了一种基于材料基因工程的复合固体推进剂力学性能预估方法。材料基因指推进剂配方、组分的分子结构及聚集态结构、组分之间的相互作用等，这些参数是推进剂力学性能的内在因素。基于材料基因工程的复合固体推进剂力学性能预估的内核即从配方入手，构建材料基因与推进剂性能之间的映射关系，从而实现基于配方的材料性能预估。

本研究针对AP/Al/HTPB复合固体推进剂，确定了影响推进剂力学性能的材料基因，构建了材料基因与推进剂力学性能之间的构效关系，最终获得了单轴拉伸条件下推进剂内部损伤演变规律及平均应力—应变响应，初步实现了基于材料基因工程的推进剂单轴拉伸力学性能跨尺度计算。

1 填料堆积结构的最小代表性单元

复合固体推进剂固化后，多粒度级配的不同填料颗粒以类似紧密堆积的形式，均匀分散在基体中，形成填料堆积的介观微结构。填料堆积结构直接影响推进剂内部的应力分布，是决定推进剂力学性能的重要基因之一。

作为推进剂力学性能预估的几何模型，填料堆积结构模型应以反映真实推进剂粒度级配为首要前提，并兼顾计算规模及效率。基于表1所示的某AP/Al/HTPB推进剂的填料级配，建立了填料堆积结构最小代表性单元[7]。最小代表性单元中，各级颗粒的粒径序列依次取为推进剂配方中各级颗粒粒径，各级颗粒的数量序列取为1 mm3推进剂中各级填料颗粒数量序列的最小整数比。在最小代表性单元(等边立方体)的平均密度等于真实推进剂密度的前提下，可唯一确定最小代表性单元的体积及边长。

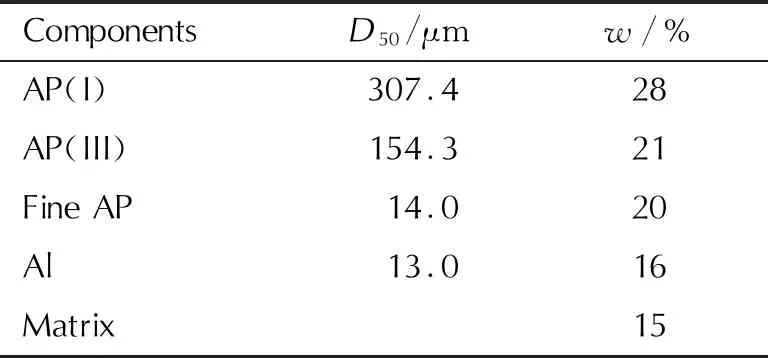
表1 AP/Al/HTPB推进剂配方Table 1 Formulation of AP/Al/HTPB propellant

对于表1所示推进剂填料粒度级配，计算得到最小代表性单元边长(L)为0.39 mm。单元中I类AP、III类AP、超细AP和Al颗粒的数量序列为1、6、7168和5575。

为获得最小代表性单元中颗粒的分布状态，首先针对数量较少、且粒径较大的Ⅰ类AP和Ⅲ类AP，采用遗传算法，获得互不重叠且均匀分布的粗颗粒堆积结构；再基于改进的L-S算法[8]，将剩余细颗粒(超细AP、Al)随机填充至粗颗粒堆积结构间隙。最终获得推进剂填料堆积结构的最小代表性单元，结果如图1所示。

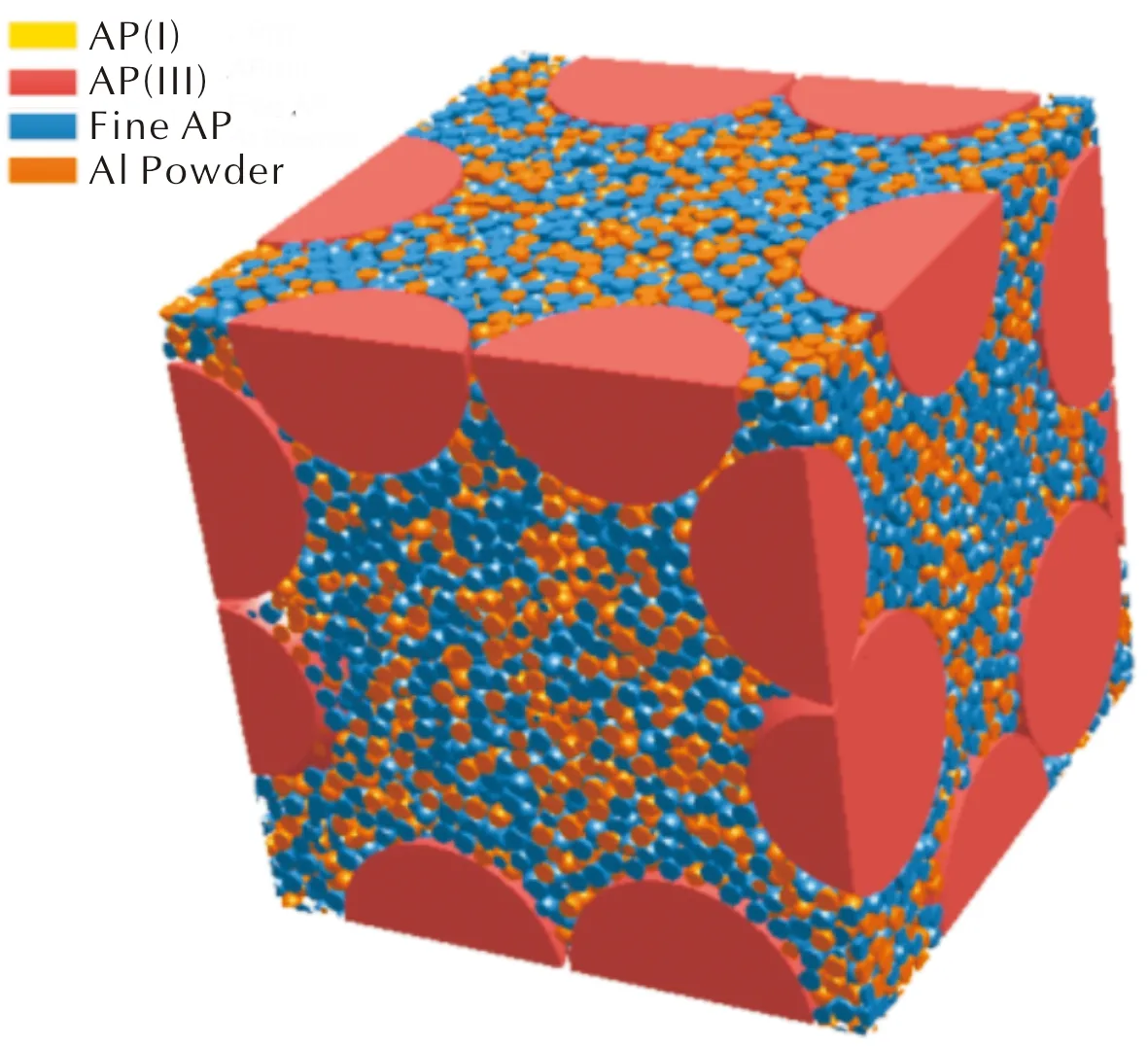
图1 填料堆积结构最小代表性单元Fig.1 The minimum representative unit of the filler packing structure

考虑到基于三维填料堆积结构进行有限元计算时，网格划分难度及计算量较大、对数值求解方法要求更高。可采用填料堆积结构的若干二维切面进行简化计算，再采用统计平均获得三维结构的近似结果。本研究后续计算以X=L/6(L为最小代表性单元的边长)处切面为例，切面处填料堆积形貌如图2所示。

图2 X=L/6处填料堆积结构的切面形貌Fig.2 Cross section morphology of the filler packing structure at X=L/6

2 复合固体推进剂的本构关系

复合固体推进剂力学性能由填料、基体、填料-基体黏接界面的本构关系共同决定。

2.1 填料的本构关系

单轴拉伸过程中，刚度较大的填料颗粒变形较小，则填料的本构关系可采用线弹性平面应变模型描述。此时，决定填料力学性能的材料基因包括填料颗粒的弹性模量(E)和泊松比(v)。对于AP和Al颗粒，取值分别为：

EAP=32 450 MPa,vAP=0.14
EAl=68 300 MPa,vAl=0.33

2.2 基体的本构关系

推进剂基体本质上为黏弹性交联网络及嵌于其中的增塑剂，也可称为增塑的交联弹性体。黏合剂交联网络由黏合剂聚预聚物、固化剂和交联剂之间的固化交联反应形成。

根据Gaussian模型，交联弹性体的本构关系可表示为：

σGauss=α·εGauss

(1)

式中：α为交联高聚物弹性体的模量；εGauss为基于Gaussian模型的应变，可表达为：

(2)

式中：ε为工程应变。

考虑大变形条件下交联高聚物弹性体的非仿射变形，模量α可表达为[9]：

(3)

式中：fCL为交联弹性体中交联剂的官能度；R0为普适气体常数；T为测试温度；δB为黏合剂预聚物分子的空间位阻参数；ρnet为交联弹性体的交联密度，包含化学交联密度ρnet-ch和物理交联密度ρnet-phy。

对于HTPB/二异氰酸酯(NCO)/三羟基交联剂(CL)固化体系，将固化体系中HTPB贡献的羟基摩尔数和三羟基交联剂贡献的羟基摩尔数之和定义为总羟基摩尔数，即

n(OH)T=n(OH)HTPB+n(OH)CL

(4)

将固化体系中异氰酸酯基摩尔数与总羟基摩尔数之比定义为固化参数RNCO/T-OH

RNCO/T-OH=n(NCO)/n(OH)T

(5)

将固化体系中三羟基交联剂贡献的羟基摩尔数与总羟基摩尔数之比定义为交联参数RCL-3OH/T-OH

RCL-3OH/T-OH=n(OH)CL/n(OH)T

(6)

则固化体系中黏合剂HTPB贡献的羟基摩尔数与总羟基摩尔数之比RB-OH/T-OH可表示为：

RB-OH/T-OH=1-RCL-3OH/T-OH

(7)

则化学交联密度ρnet-ch可表示为:

(8)

式中：fNCO和fCL分别为固化剂异氰酸酯和交联剂的官能度；MNCO和MCL分别为固化剂和交联剂的摩尔质量；ρNCO、ρCL和ρB分别为固化剂、交联剂和HTPB的密度；EB-OH为HTPB的羟值。

交联密度还应考虑物理交联密度及增塑剂含量、黏弹性的影响，具体可参考文献[9]。基体本构关系的主要材料基因构成及取值分别为：δB=1.463；fCL=3；RNCO/T-OH=1.0；RCL-3OH/T-OH=0.15。

2.3 填料-基体界面的本构关系

为了刻画载荷作用下填料-基体界面可能出现的黏接刚度退化、黏接失效以及造成的填料脱湿，采用双线性模型[10]描述填料-基体界面本构关系。双线性模型示意图如图3所示，横坐标为填料-基体界面单元张开位移，纵坐标为内聚力。该模型下，决定填料-基体界面本构关系的基因组包括3个参数：(1)初始刚度K，即AB段斜率；(2)内聚力强度Tmax，即B点处内聚力的最大值；(3)界面结合能Ubind，即内聚力—张开位移曲线围成的面积。当界面单元张开位移大于C点对应值时，认为填料-基体界面单元失效，对应位置发生脱湿。

图3 双线性内聚力模型示意图Fig.3 Schematic diagram of the bilinear cohesive model

填料-基体界面结合能是填料-基体界面本构关系的材料基因，可通过分子动力学方法计算获得[11]。填料-基体界面性质本质上是填料和键合剂之间的相互作用决定，HTPB推进剂中键合剂常选用三氟化硼三乙醇胺络合物(T313)。

填料-基体界面结合能的计算方法：首先，根据AP、Al填料颗粒的XRD谱图，计算获得填料的主晶面信息;然后，采用分子动力学方法，获得T313键合剂分子链的无定形模型；最后，将键合剂分子链的无定形模型切面，并添加到填料主晶面，充分弛豫至平衡后，通过单点能分别计算得到填料的能量Ufiller、键合剂的能量UT313、填料-键合剂混合体系的能量Utotal，则填料-基体界面结合能Ubind可表达为：

Ubind=-[Utotal-(Ufilller+UT313)]

(9)

计算得到AP(0 0 1)、(2 0 1)、(2 1 0)3个主晶面及Al(1 1 1)晶面与T313键合剂的界面结合能分别为1.99、1.89、1.58及0.51 J/m2。周红梅等[12]采用接触角测量实验获得AP-HTPB界面结合能为0.32 J/m2，与采用分子动力学计算得到的结果数量级较接近，可验证方法的可靠性。后续计算中，AP颗粒与基体的界面结合能取为AP三个晶面与T313键合剂结合能的平均值，即1.82 J/m2；Al颗粒与基体的界面结合能取0.508 J/m2。初始刚度取1.2 MPa/mm，内聚力强度取0.5 MPa。

3 计算结果与细观破坏过程分析

根据前文建立的填料堆积结构最小代表性单元和构建的材料本构关系，基于ABAQUS平台，模拟单轴拉伸条件下推进剂的力学行为。几何模型取为图2所示X=L/6处填料堆积结构的二维切面，并拆分为填料、基体和填料-基体界面3个部件。依据构建的模型，直接输入关键参数定义填料和填料-基体界面的本构关系，通过编写UMAT用户子程序定义较为复杂的基体本构关系。取最小代表性单元下边界为固定边界条件，位移载荷施加于单元上边界。各时刻下，取代表性单元上边界各网格节点应力的平均值，作为单轴拉伸过程对应时刻推进剂的应力。

图4为拉伸过程不同应变下，最小代表性单元内的应力分布及界面脱湿情况。图5红色实线为基于代表性单元获得的推进剂应力—应变曲线，曲线上a～f各点分别对应图4(a)～(f)的6个特征时刻。为进一步验证计算结果，制备了相同配方的推进剂并进行单轴拉伸测试，获得实测应力—应变曲线，结果如图5蓝色虚线所示。

图4 单轴拉伸过程不同应变下推进剂的应力分布及界面脱湿情况Fig.4 Stress distribution and interface dewetting of the propellant at different strains during the uniaxial tension

图5 最小代表性单元的应力—应变曲线Fig.5 The stress—strain curves of the minimum representative unit

依据图5推进剂应力—应变曲线，并结合图4所示内部应力分布云图，将拉伸过程分为5个阶段：

(1)I阶段为初始模量弹性段(ε<6.05%)。小变形条件下，黏合剂基体处于玻璃态，变形由高分子键长、键角变化引起，表现为弹性特征。同时，填料-基体界面内聚力足以抵抗外部较小的应力，因此，由图4(a)看出，I阶段填料-基体界面均黏接完好，填料的补强作用得以充分发挥。在图5的I阶段，推进剂单元的应力以近乎直线的形式迅速增加，推进剂初始模量为6.98 MPa。随应变增加，填料-基体界面呈现不同程度的应力集中。各相的平均应力大小顺序为：填料-基体界面>粗颗粒内部及基体>细颗粒内部。

(2)II阶段为黏弹性段(6.05%≤ε<15.37%)。当应力—应变曲线经过点a后，受基体黏弹性作用，在弹性段不可运动、处于无规缠绕状态的黏合剂开始沿拉伸方向取向伸展，同时黏合剂弹性体交联密度下降，导致推进剂的黏弹性模量下降，应力增加速率低于应变增加速率，应力—应变曲线偏离线性段，进入黏弹性段。该阶段内，尚未发生填料脱湿或基体微裂纹等损伤。如图4(b)，当应变为13.16%时，计算域内所有填料-基体界面黏接完好。

(3)III～V阶段为填料颗粒脱湿造成的推进剂力学性能损伤段。

III阶段为大粒径颗粒(I类AP)脱湿萌生及快速发展段。填料颗粒脱湿首先发生在粒径最大的I类AP处。由图4(c)，当ε=15.57%时，位于最小代表性单元中心的I类AP上方出现两个脱湿点。随着脱湿程度的加剧，脱湿点处界面黏结失效，应力不再能直接从基体传递至颗粒。因此，在脱湿点下方，I类AP颗粒内部应力较小。同时，脱湿形成的裂纹尖端进一步加剧了填料-基体界面的应力集中，从而加速了脱湿区域的扩展。如图4(d)，当ε=18.10%时，I类AP脱湿周长已达颗粒圆周长的近1/4。

IV阶段为大粒径颗粒(I类AP)脱湿稳定发展段。d点以后，I类AP脱湿扩展速率较慢，推进剂内部损伤无明显加剧。因此，推进剂应力—应变曲线在IV段呈现平缓趋势。

V阶段为其他粒径颗粒脱湿发展段。如图4(e)，当ε=21.19%时，中等粒径的III类AP开始脱湿。随后，III类AP脱湿面积逐渐增加，当ε=21.19%时，III类AP脱湿周长已达近1/5。

与实际推进剂单轴拉伸应力—应变曲线相比，计算得到的曲线可以较好地反映单轴拉伸载荷下推进剂力学响应的变化趋势。但在损伤段，实际推进剂应力—应变曲线下降更为平缓，且应力的极大值略高于计算获得的应力极大值。原因在于：由填料-基体界面脱湿造成的推进剂力学性能损伤多发生在粗粒径颗粒处，而本研究构建的最小代表性单元中粗粒径颗粒数量较少。因此，单个颗粒的脱湿对整体计算结果影响较大。后续在计算能力允许的条件下，可以考虑适当增加计算单元大小。

综上所述，对于本研究所讨论的HTPB推进剂体系，填料脱湿发生在应力—应变曲线中黏弹性段的后期。填料脱湿对推进剂力学性能的影响表现为推进剂黏弹性模量的进一步下降，具体影响规律与填料颗粒的尺寸及分布有关。

4 结 论

(1)填料堆积微结构是决定推进剂力学性能的关键基因之一。构建了可反映推进剂配方(填料粒度级配)且兼顾计算量的填料堆积微结构最小代表性单元。

(2)复合固体推进剂中，决定填料力学性能的材料基因指填料的模量及泊松比；决定基体力学性能的材料基因包括黏合剂预聚物的空间位阻、固化体系的固化参数及交联参数、交联剂的官能度等；决定填料-基体界面力学性能的材料基因包括界面内聚能、内聚力强度和初始刚度。分别构建了上述材料基因与填料、基体、填料-基体界面力学性能之间的构效关系。

(3)单轴拉伸条件下，AP/Al/HTPB推进剂的应力—应变曲线可分为弹性段、黏弹性段和损伤段3个阶段。基体的黏弹性和填料-基体界面脱湿均会导致推进剂黏弹性模量下降，填料脱湿发生在推进剂应力—应变曲线在黏弹性段的后期，导致推进剂黏弹性模量的进一步下降。

谨以此文纪念张炜教授！