基于量子遗传的超参数自动调优算法的设计与实现

吴浩楠 高宏

摘 要：机器学习伴随着海量数据的支持以及强大的计算能力为其提供了强有力的保证下不断地向前发展，训练过程变得更加高效便捷。在此基础上，机器学习算法的超参数对其性能的影响是非常巨大的，因此对众多的超参数进行优化选择就自然有了强烈的需求。由此本文提出了一种基于量子遗传的超参数自动调优算法，实验表明，在针对多种机器学习模型的超参数调优问题上，既解决了一般随机算法的不稳定性的问题，也解决了一般进化算法迭代缓慢、收敛速度较低的问题，并且通过实验结果表明取得了不错的效果。

关键词： 超参数调优;遗传算法;量子遗传算法;机器学习

文章编号： 2095-2163（2021）01-0170-06 中图分类号：TP181 文献标志码：A

【Abstract】With the development of big data and the improvement of computing power， machine learning has been continuously developing， and the training process has become more efficient and convenient. On this basis， the hyper-parameter of machine learning algorithms has a great impact on their performance， so there is a strong demand for optimizing and selecting a large number of hyper-parameter. Thus this paper puts forward a kind of automatic tuning super parameter based on Quantum Genetic Algorithm. The experiments show that for a variety of machine learning model on the above parameters tuning problem，the instability of both randomized algorithms of the general problem is solved， also the problems of slow iteration and low convergence speed of the general evolutionary algorithm are solved， therefore good results have been achieved.

【Key words】hyper-parameter tuning; Genetic Algorithm; Quantum Genetic Algorithm; machine learning

0 引 言

如今，海量数据的支持以及强大的计算能力为机器学习的不断发展提供了有效保证，使其训练过程变得更加高效、便捷。在此基础上，一个机器学习算法的超参数就成为影响算法性能优劣的重要因素。如何在复杂的参数空间中选择出一组超参数使得机器学习算法的性能得到最大的提升，是机器学习领域长期以来一类备受关注的研究问题，超參数优化问题也是在此背景下才得以提出。

研究初期，一般需要相关的工作人员通过已有的经验对超参数进行调节，或者是由设计者给出建议的超参数的配置选择。但在模型复杂以及超参数众多的情况下，就随即对超参数进行自动化调优有了强烈的需求。故而，对于机器学习算法未来走向实用，设计出一个超参数自动调优算法则有着至关重要的现实意义[1]。

早期，网格搜索（Grid Search）是超参数优化算法中常用的技术。但是网格搜索方式的效率是很低下的，其本质是属于穷举的方法，只不过是带有一定的步长。超参数的搜索空间，会随着待优化参数的增加，而呈指数型增长[2]。文献[3]中讨论了一种随机搜索策略，并通过实验表明，与网格搜索方法相比，该方法有着更高的效率。文献[4]还提出了TPE算法，解决了机器学习超参数优化问题，该算法是基于模型的全局优化并且是树形结构的。此外，贝叶斯优化也是该领域较经典的超参数优化算法，具体就是一种快速求解昂贵函数极值问题的优化方法[5]。

在国内的有关超参数优化的文献中，大多是利用进化算法来进行机器学习模型的超参数调优。例如，文献[6]中的超参数优化方法是模拟退火算法;文献[7]中，运用遗传算法来解决机器学习模型支持向量机（SVM）的超参数优化问题;此外常见的还有粒子群优化算法[8]。实际上在处理超参数优化问题时可将其视作针对昂贵函数来进行优化。并且进化算法中大部分都是基于种群的，当种群规模较大时则会同时伴生着与算法性能效率相关的问题。因此，本文拟基于一种量子遗传算法，其类属于进化算法，来提出主要研究内容，即一种基于量子遗传的超参数自动调优算法。通过实验表明，本文提出的算法在解决机器学习模型的超参数优化问题的同时，在对比实验中还取得了性能和效率上的提升。

1 超参数优化问题表述

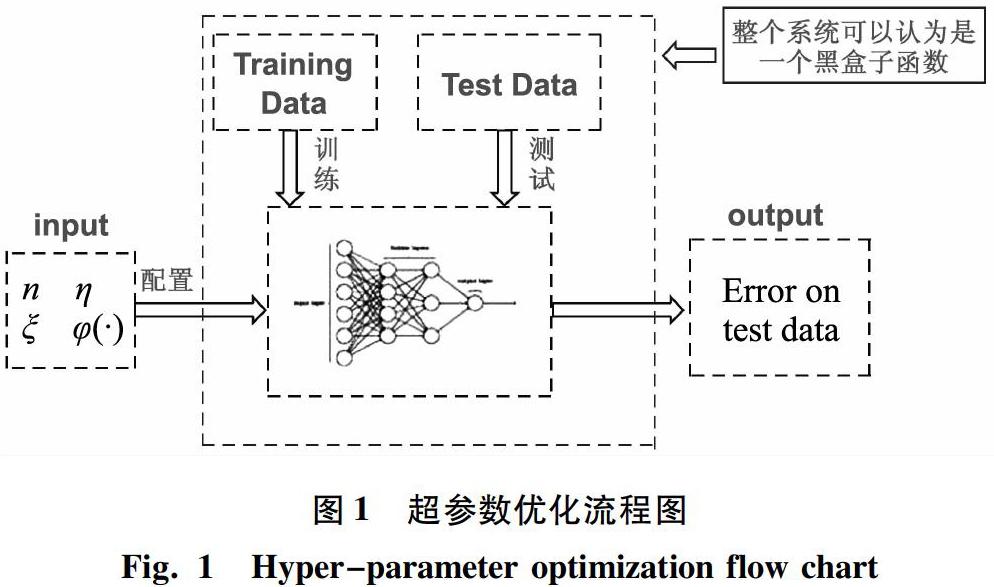
超参数优化的思想对机器学习的调参有着重要意义，对于其他复杂的系统结构，当研究过程需要优化这一类黑箱模型结构时，都可以借鉴超参数优化的思想来解决系统的结构优化问题。本文研发设计的基于量子遗传的超参数优化算法是应用于解决传统机器学习模型的超参数调优问题。如图1所示。由图1可知，主要是模拟了超参数优化问题的大致过程。

研究可知，该问题的本质就是为机器学习模型找到一组较好的超参数配置，使得机器学习模型在测试集合上的泛化误差达到最小。此后提到的相关实验过程及结果是基于GBDT机器模型来进行的超参数调优相关实验。GBDT是常用传统机器学习模型，可解决大部分机器学习中分类和回归问题，与其相关的超参数分为2类：boosting框架参数，弱学习器即CART回归树相关的重要参数。相关超参数见表1。

2 基于量子遗传的超参数调优算法

2.1 量子遗传算法

量子遗传算法源于量子计算，同时也是一种进化算法。量子遗传算法在本质上还是一个基于概率的随机搜索算法[9]。

在探讨量子遗传算法前，则需要了解一些与量子计算相关的知识作为理论基础。首先，要知道量子位是量子计算中存储信息的最小单元，量子位可以表示为：αβ，其中满足α2+β2=1。接下来是量子门，在量子遗传算法中量子位是可以通过量子门来改变的，将其引入不仅使得算法具备了开发和探索的能力，还使得算法能够最终走向收敛[10-11]。量子门是一个2×2阶的可逆矩阵U，量子门一般通过如下矩阵变换更新量子位，设新的量子位为αiβi，那么：

接下来在量子位的基础上，又引出了量子染色体的概念，每一个染色体都是由式（2）中的一系列量子位组成的，即：

量子遗传算法的大致流程，参见算法1。

算法1 量子遗传算法

输入：种群大小N，算法的终止条件（比如迭代次数等）

输出：集合B中表现最好的样本

Step 1 生成输入指定大小量子染色体种群Q（t），并对其进行初始化操作。

Step 2 将种群Q（t）中每一个量子染色体通过规则进行转换为一个二进制串，形成一个新的二进制串的集合P（t）。

Step 3 对P（t）中的每个样本通过目标函数进行评价。

Step 4 将Step 3中表现最优的样本添加到集合B中。

while（如果未满足终止条件）

{

Step 5 进行下一次迭代，令t=t+1，对量子染色体种群Q（t-1）进行Step 2的操作，从而形新一轮的P（t）。

Step 6 对P（t）中的每个样本通过目标函数进行评价。

Step 7 将Step 6中表现最优的样本添加到集合B中。

Step 8 将种群Q（t）通过量子门的旋转进行更新进化。

}

2.2 基于量子遗传的超参数调优算法

在本小节中，给出算法的基本框架见算法2。

算法2 基于量子遗传的超参数调优算法

输入：待优化机器学习模型M，数据集X，种群大小N，这里設置为1，待优化的超参数的参数空间，算法的终止条件（比如迭代次数等）

输出：集合B中表现最好的样本

Step 1 生成指定规模大小量子染色体种群Q（t），并对其进行初始化操作。将输出集合B置为空集。通过超参数的类型及参数空间决定量子染色体的总长度。

Step 2 将种群Q（t）中每一个量子染色体通过规则进行转换为一个二进制串，形成一个新的二进制串的集合P（t）。

Step 3 对P（t）中的每个样本通过目标函数进行评价。将每个二进制串解码为一组赋有特定取值的超参数配置。评估机器学习模型M在此超参数配置下进行训练后，在测试集上的性能指标，并将该结果作为目标函数的输出。

Step 4 将Step 3中表现最优的样本添加到集合B中。

while（如果未满足终止条件）

{

Step 5 进行下一次迭代，令t=t+1，对种群Q（t-1）重复上述Step 2中操作，生成新一轮的集合P（t）。

Step 6 重复Step 3对P（t）中的样本进行评价。

Step 7 重复Step 4更新集合B。

Step 8 将种群Q（t）通过量子门的旋转进行更新进化。

}

这里，对于算法2中的关键步骤含义拟做出分析详述如下。

Step 1中，本质是在对每个超参数进行编码操作，进而决定量子染色体的总长度。研究中是基于以下方案来确定量子染色体的总长度。超参数一般有2种类型：离散、连续。假设某个超参数是离散类型的，并且只有3种取值，这时通过2位量子位就可以编码表示该参数的所有状态。例如可以用00，01，10分别对应表示该超参数的一种状态。相应地，对于编码为11的状态，算法中的规定是：可以对其进行随机变异，使其转变为上述三种编码状态中的任意一种。而对于连续型超参数来说，例如某超参数取值范围在区间[a，b]，可以根据研究中自定义的精度来将其分割成k份。那么就需要N位来编码这个超参数，这里N需要满足如下条件：

Step 2的本质就是在对量子染色体进行一个转换，将其转换为一个二进制串。具体实现过程为：针对量子染色体中的每一位，都要先生成一个随机数r，取值在[0，1]之间，若rα2，则该位置为0，否则置为1。下面将举例说明上述操作。例如，某条量子染色体可以表示为1212，1212，1212，针对其中的每一位量子位随机生成的数字为0.3、0.7、0.2，那么对该量子染色体进行观察操作后，得到的二进制串可以表示为[0，1，0]。与此过程相似，还将对每个量子染色体都重复进行上述观察操作，最后形成了上述算法中提到的种群 P（t）。

Step 3在本质上是对每一个在Step 2中转换好的二进制串进行解码操作，将其翻译为每一个超参数所对应的实际取值。具体操作为：由于此前提到过超参数分为离散型和连续型两种，那么过程中的解码操作也相应地分为2种。

总地来说，对于超参数是离散型情况下的解码，可以提前定义一张映射表。其中，key对应的是Step 2中转换的二进制串中的某一段，value对应的是该段二进制串在事先定义好的映射表中对应的实际值。而当超参数是连续型的情况时，可以通过式（4）来进行计算：

其中，x为代表该超参数那段的二进制串对应的十进制数;a和b分别表示该参数取值范围的上限和下限;N表示该段二进制染色体的总体长度，而等式左侧的x即为连续型超参数通过解码操作后计算得到的实际取值。

Step 4则是执行Step 3后，在比较后记录下有着较好适应度的个体。

Step 7的本质就是利用此前涉及到的量子旋转门，来对旧的量子染色体进行更新进化，形成新一轮的量子染色体，在量子遗传算法中，由于量子编码作用下的染色体不再是单一的纯态，遗传处理中不能继续仅仅采用传统的选择/交叉/变异等操作，而是要采用量子旋转门作用于量子染色体的基态，使其相互干涉，相位发生变化，从而改变概率幅的分布。综上论述可知，量子旋转门的设计是整个算法框架里的核心步骤。对其实现过程将依次展开如下论述。

前文提到过，每一个量子位是通过量子旋转门进行更新的，对此可表示为：

进一步，旋转门U可表示为：

其中，θ表示本次的旋转角度，该值大小与符号在量子位的更新过程中占据着举足轻重的地位。研究中给出了量子位的旋转演示如图2所示。

由图2可知，θi的正负情况将决定量子门的旋转方向。若θi为正，更新后的量子比特位α将会减小，相应地将提高其为1的概率;相反，若θi为负，更新后的量子比特位α将会增大，相应地将提高其为0的概率。这里，对θi的设计可表述为：

其中，Δθi表示旋转角度大小;s（αi，βi）表示其正负情况，设ri和bi分别表示当前个体和当前最优个体的第i个量子位的二进制取值，则此时对应的θi可通过对表2的计算得到。

2.3 基于量子遗传的超参数调优算法的改进及完善

依据2.2节提出的基于量子遗传的超参数调优算法框架，本文对该算法进行了改进与完善。如前所述，该算法中量子旋转门的设计是整个算法框架的重中之重，故而尝试将原有的量子位更新方法改为了如下形式：

上述量子门为Hardmard门，也叫做相位门。使用此方式对量子位操作时，可以改变旋转相位，也可以进行将量子位旋转90°的操作。该方式实现了遗传算法中经常会提到的变异操作，因此就通过将原算法中的量子旋转操作改为使用Hardmard门，实现对量子染色体的变异，这就在一定程度上避免早熟现象的发生。

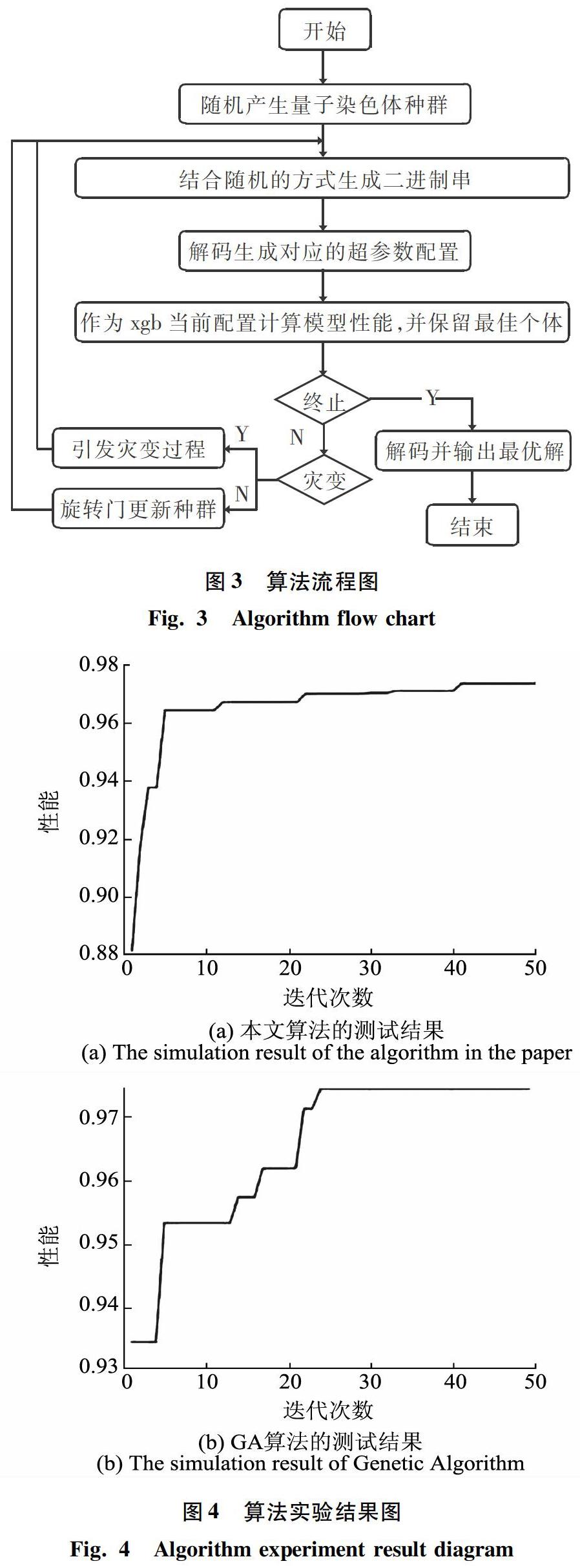
此外，对算法过程的完善操作即是在最后加入了量子灾变过程。也就是说，当运算中连续多次都没有进化发生后，此时就要引发量子灾变过程，将新一轮的量子染色体重新初始化初值，再继续正常向下运行算法，如此即可在一定程度上避免陷入局部最优。本文提出的基于量子遗传的超参数调优算法的流程如图3所示。

3 实验

为了验证本文提出算法的有效性，本小节拟进行一些对比实验。首先是与基因遗传算法（GA）的执行测试结果进行比较，2种算法执行过程中的迭代收敛曲线如图4所示。横坐标表示迭代次数，纵坐标表示模型在每轮迭代训练后的执行性能。

由图4可以看出，基于量子遗传的参数优化算法收敛速度要快于GA算法，并且最终都使得机器学习模型在优化结束后获得较好的性能。

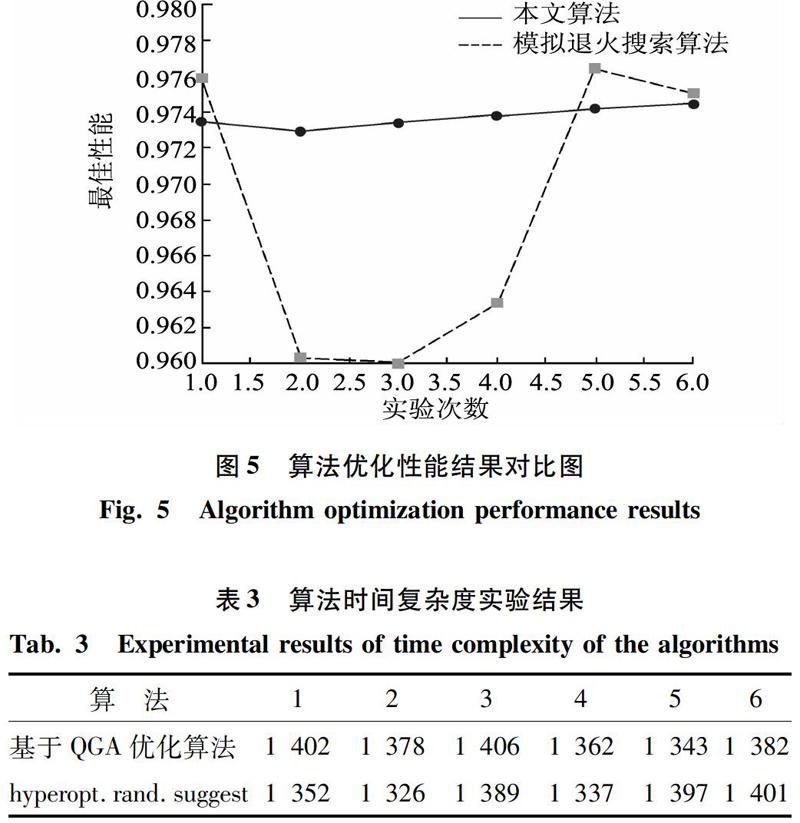
接下来是与模拟退火搜索算法相比较，结果如图5所示。图5中实线表达的是本文所提出算法的实验结果。横坐标表示实验次数，纵坐标表示每次实验后模型在优化算法执行过程中达到的最好性能。

从图5分析可知，由于对比算法存在一定概率随机搜索，即使得相比之下本文提出的優化算法的执行结果明显更加稳定。

同时，还与概率随机搜索算法进行对照，研究得到的算法时间复杂度的结果对比见表3。

由表3可以看出，本文提出的调优算法在时间复杂度上与随机搜索算法相差无几，并就之前提到的基于种群的进化算法的时间效率问题得到了很好的解决。

最后，将本文算法应用在其他的模型优化场景中进行测试，测试结果见图6。

由图6可知，本文提出的优化算法应用在其他传统机器学习模型的超参数优化问题中也有良好表现。

4 结束语

本文提出了一种基于量子遗传的超参数自动调优算法。

首先，该算法是结合了进化算法和概率随机搜索两者的核心思想。进化算法在使用时大部分是基于种群的方法，比如一些进化遗传算法，粒子群优化算法等，如果把种群个数设置为 1，这些算法就失去了作用，因其每次迭代需要互相之间的信息交互。但是量子遗传与之不同的地方就在于，该算法是由相互独立的每个个体组成，每次更新均是通过旋转门来实现的，所以当种群的规模为1时，算法也可以正常执行。所以本文所提算法在时间复杂度上与前者近似，两者均为在每一轮迭代中进行一次模型性能评估，这也解决了一般进化算法迭代缓慢、收敛速度较低的问题。

其次，本文算法也继承了遗传进化算法的特性，量子染色体通过旋转门的操作使得每个量子位都在朝着好的方向进化，如此一来就使得相比于前者来说，算法的执行结果更加稳定。

同时，本文算法在其他模型优化问题中有较好的表现，说明本文算法也具有一定的通用性。

最后，通过实验结果分析表明，本文算法在解决超参数调优问题上具有可行性及有效性。而将该算法思想应用于解决更多的超参数优化问题场景上，则是未来后续工作中的重点研究内容。

参考文献

[1]陆高. 基于智能计算的超参数优化及其应用研究[D]. 西安：西安电子科技大学，2018.

[2]LERMAN P M. Fitting segmented regression models by grid search[J]. Applied Statistics，1980，29（1）：77-84.

[3]BERGSTRA J， BENGIO Y. Random search for hyper-parameter optimization[J]. Journal of Machine Learning Research， 2012， 13（10）：281-305.

[4]BERGSTRA J S， BARDENET R， BENGIO Y， et al. Algorithms for hyper-parameter optimization[C]//25th Annual Conference on Neural Information Processing Systems（NIPS 2011）. Granada， Spain：dblp， 2011： 2546-2554.

[5]BROCHU E， CORA V M， De FREITAS N. A tutorial on Bayesian optimization of expensive cost functions， with application to active user modeling and hierarchical reinforcement learning[J]. arXiv preprint arXiv：1012.2599， 2010.

[6]燕飞， 秦世引. 一种基于模拟退火的支持向量机超参数优化算法[J]. 航天控制， 2008，26（5）：7-11，17.

[7]唐静， 胡云安， 肖支才. 基于遗传算法的电路故障诊断超参数优化算法框架[J]. 计算机工程与应用， 2012， 48（3）：13-16.

[8]GUO X C， YANG J H， WU C G， et al. A novel LS-SVMs hyper-parameter selection based on particle swarm optimization[J]. Neurocomputing， 2008， 71（16-18）：3211-3215.

[9]焦李成， 李阳阳， 刘芳，等. 量子计算、优化与学习[M]. 北京： 科学出版社， 2017.

[10]周传华，钱峰. 改进量子遗传算法及其应用[J]. 计算机应用，2008，28（2）：286-288.

[11]张秋艳，王默玉，申晓留，等.基于灾变因子的量子遗传算法研究[J].计算机与数字工程，2019，47（7）：1591-1595.