有向图上k步可达查询处理

杜明 林铿 周军锋

摘 要：给定一个有向图，一个k步可达查询u→？kv用来回答在该图中是否存在一条从顶点u到顶点v且长度不大于k的有向路径。k步可达查询是一种基本的图操作并在过去十年间被广泛地研究。已有的k步可达查询算法仍存在许多弊端，例如不可达查询效率低，索引规模大和索引构建时间长等。本文针对上述问题提出了2种优化方法，分别是基于互逆拓扑序号以及基于等价顶点的图压缩方法.前者提高了不可达查询的效率，后者减少了索引规模和索引构建时间。实验结果表明，本文提出的方法可以有效地处理k步可达查询，并支持大规模数据的处理。

关键词： 有向图;k步可达查询;图压缩

文章编号： 2095-2163（2021）01-0008-07 中图分类号：TP301.6 文献标志码：A

【Abstract】Given a directed graph， a k-hop reachability query u→？kv is used to answer whether there is a directed path from vertex u to vertex v and the length of the path is not greater than k. The k-hop reachability query is a basic graph operation and has been extensively studied in the past years. Existing algorithms still have many drawbacks， such as being inefficient for unreachability queries， large index size and long index construction time. This paper proposes two optimization approaches to make improvements， i.e.， the mutual reversed topological order and the graph compression based on equivalent vertices. The former improves the efficiency of unreachability queries， and the latter reduces the index size and index construction time. The experimental results show that the proposed method can effectively improve the performance of k-hop reachability queries processing and support large-scale graph processing.

【Key words】directed graph; k-hop reachability query; graph compression

0 引 言

隨着互联网的快速发展，各种数据的规模日益庞大。图是一种常见的数据表示模型，其中每个实体被简单地抽象成图中的一个顶点，实体间的关系被抽象成2个顶点之间的一条边。图被广泛地应用于各类领域，如社交网络、通信网络、交通网络等等[1-3]。在图模型上的一个基本操作是回答2个顶点之间的可达性查询，即判断在图中是否存在一条从源顶点u出发到目标顶点v结束的一条有向路径。可达性查询在过去被广泛地研究[4-8]，然而在实际应用中，可达性查询仅能回答2个实体之间是否存在某种关系，而无法回答这种关系的强弱程度。

另一种更有价值的操作是回答2个顶点之间的k步可达查询[9-10]，即判断在图中是否存在一条从源顶点u出发到目标顶点v结束的一条有向路径，并且满足该路径的长度不超过k。k步可达查询相较于可达性查询能提供更多关于2个顶点之间的信息，本质上，可达性查询是一种特殊的k步可达查询，即当k取∞时。k步可达查询在现实生活中有很多实际的应用。比如在交通网络中，经常需要回答在2个地点之间是否存在一条路程不超过某个阈值的路线。又比如在社交网络中，通过2个实体之间的距离来判断这2个实体产生关联的可能性。

现有k步可达查询算法大多只能运行在有向无环图上，而有向图上的k步可达查询的相关研究却寥寥无几。在有向图上回答k步可达查询的基本方法是BFS[11]或者DFS [12]。基于遍历的方法因为不具备良好的扩展性，因而查询效率低下。另一个简单的实现方法是将任意2个顶点之间的最短路径信息预先通过邻接矩阵的方式存储起来，回答查询时仅需要O（1）的时间内即可返回结果。但是这种方法需要的空间代价过大，无法应用于大规模数据图。

针对上述算法存在的问题，文献[9]提出了一种基于2-hop索引PLL。PLL的基本思想是通过为每个顶点预先建立一组出标签和一组入标签，这2组标签分别保存了部分顶点与该顶点之间的最短路径信息，这些部分顶点被称为hop点。2个顶点之间的k步可达查询问题可以被转化为判断两点间最短路径的长度是否小于等于k的问题。

PLL算法本身也存在低效性的问题。首先，如果一个查询顶点对之间是不可达的，那么PLL算法需要遍历源顶点的所有出标签以及目标顶点的所有入标签才能判断出这对查询顶点对是不可达的。其次，PLL算法在所有的顶点上构建索引，因此导致构建的索引的时间较长，同时构建的索引规模也较大。

针对PLL算法存在的以上2种问题，本文提出了2种针对性的优化方法。第一种是基于互逆拓扑序号来加快不可达查询的效率，第二种是基于等价顶点的图压缩方法，通过去除图中的冗余顶点和冗余边，使得图尽可能地小。实验结果表明，本文提出的优化方法可以显著改善索引的构建速度，索引规模更小。

1 相关工作

1.1 问题定义

给定一个有向图G=（V，E），其中V={v1，v2，…，vn}是图中顶点的集合，E={（u，v）|u，v∈V}是图中边的集合。当一条边e=（u，v）∈E时，表示存在一条从顶点u指向顶点v的有向边。对于每个顶点u，本文使用scc（u）来表示顶点u所在的强连通分量。同时使用outG（u）={v|（u，v）∈E}来表示顶点u的出邻居集合以及使用inG（u）={v|（v，u）∈E}表示顶点u的入邻居集合。用degout（u）=|outG（u）|表示顶点u的出度，degin（u）=|inG（u）|表示顶点u的入度。

在一个有向无环图中，拓扑排序是将图中顶点从偏序状态转化为全序状态。一个顶点u的拓扑序号是顶点全序关系的序号，拓扑序号大的顶点与拓扑序号小的顶点之间不存在有向路径。

如果2个顶点u，v满足outG（u）=outG（v）并且inG（u）=inG（v），即顶点u和顶点v存在相同的出邻居集合以及相同的入邻居集合，则称这2个顶点互为等价顶点。直观上，2个顶点等价意味着二者可达相同的顶点集合，且可达二者的顶点集合也相同。

问题定义 给定一个有向图G和一个k步可达查询u→？kv，如果在G中存在一条从u出发到v的有向路径，并且该路径的长度不超过k，则返回TRUE，否则返回FALSE。

1.2 相关算法

1.2.1 PLL算法

PLL（Pruned Landmark Labeling）算法的基本思想是为图中的每一个顶点u预先构建2组标签Lout（u）={（h1，d1），…，（hi，di）}和Lin（u）={（h1，d1），…，（hj，dj）}。其中，Lout（u）保存了从顶点u可以到达的部分顶点以及顶点u到这些顶点之间的距离，类似地，Lin（u）保存了从部分可以到达顶点u的顶点以及这些顶点到顶点u之间的距离。每个顶点标签中的每一对元素（h，d）表示hop点h以及h和该顶点之间的最短距离d。

PLL算法将2个查询顶点对之间的k步可达查询转化为了判断源顶点u和目标顶点v的最短距离是否小于等于k的问题。由于标签中的hop点序号是以升序排列的，因此判断2个标签中是否存在一个公共的hop点的时间复杂度为O（n+m），其中n，m分别表示出标签和入标签中元素的个数。

PLL算法使用剪枝策略保证了建立的索引中尽可能地减少冗余的最短路径信息。具体的做法是在对每一个hop点进行BFS遍历的过程中，如果已经建立的2-hop索引能够回答该hop点到当前遍历的顶点之间的最短路径信息，则PLL算法不会将该hop点加入到当前遍历的顶点的2-hop标签中，同时不再从当前遍历的顶点执行BFS遍历。

1.2.2 K-Reach算法

K-Reach算法[9，13]的基本思想是首先求解有向图G的最小顶点覆盖集C，然后在求解得到的C上建立传递闭包，这个传递闭包只包含了C中各个顶点之间的可达信息。

当回答一个k步可达查询u→？kv时，根据查询顶点对u，v是否属于C分为如下3种情况：

（1）顶点u和顶点v都属于最小顶点覆盖集，此时可以直接通过建立的传递闭包来回答查询。

（2）顶点u和顶点v中只有一个属于C，在这种情况下需要通过遍历那个非最小顶点覆盖集顶点的出邻居集合的传递闭包或者入邻居集合的传递闭包来回答查询。

（3）顶点u和顶点v中都不属于C，这是最坏的情况，需要遍历顶点u的出邻居集合的传递闭包以及v的入邻居集合的传递闭包来回答查询。

K-Reach算法存在如下问题：首先该算法构建的传递闭包索引只能用于回答k等于特定值的k步可达查询。其次，当查询顶点对不属于最小顶点覆盖集时，需要遍历查询顶点对的所有邻居顶点的传递闭包。最后，随着k值的增大，每个顶点的传递闭包数量将呈指数上升，因此该算法将无法有效地扩展到大图上。

2 优化方法

2.1 基于互逆拓扑序号的查询优化方法

在有向无环图中，一个顶点的拓扑序号是该顶点在拓扑排序中被處理的顺序。如果一个顶点的拓扑序号大于另一个顶点的拓扑序号，则前者必然不可达后者，反之不成立。因此，在一个有向无环图中，可以通过判断2个顶点的拓扑序号大小来快速地回答2个顶点间的不可达情况。

但是在有向图中，由于可能存在强连通分量，而拓扑排序必须在无环图中才能进行，因此必须对有向图进行一定的变换。在本文中采取的解决方案是将每一个强连通分量（SCC）压缩成一个超级顶点，从而将有向图转换成有向无环图。Tarjan算法是用来求解强连通分量的经典算法，该算法可以在线性时间内求解出每个顶点所属的强连通分量。对于属于同一个强连通分量中的顶点，将为其赋予相同的拓扑序号。

在拓扑排序中，对于一个顶点来说，不同的处理顺序可以生成不同的拓扑序号，一个直观的想法就是为每个顶点设置多个拓扑序号从而过滤掉等多的不可达查询。然而，每个拓扑序号都需要一个整型的存储空间，过多的拓扑序号会导致索引规模增长。因此，本文提出构建互逆的拓扑序号来达到最佳的查询效率以及较小的空间开销。

互逆拓扑序号的大致思想是为每个顶点建立2个拓扑序号。如果建立顶点u的第一个拓扑序号要先于建立顶点v的第一个拓扑序号，则在建立第二个拓扑序号时，要优先处理顶点v的拓扑序号。这种机制保证了每个顶点的2个拓扑序号构成的区间尽可能地大，从而可以判断等多的不可达情况。至此，研究可得算法1、算法2的代码设计详见如下。

算法1 genTopo（G=（V，E））

输入：G=（V，E）

输出：所有顶点的互逆拓扑序号

1 G' ← tarjan（G）

2 construct（G'，X）

3 construct（G'，Y）

4 return （X，Y）

算法2 construct（G=（V，E），T）

1 將入度为0的顶点按照特定的顺序入栈S

2 topNum ← 0

3 while S≠ do

4 u ← pop（S）

5 Tu ← topNum

6 topNum ← topNum + 1

7 for each v ∈outG（u） do

8 degin（v） ← degin（v）-1

9 if degin（v） = 0 do

10 push（S，v）

算法1展示了在一个有向图上求解互逆拓扑序号的过程。算法的输入是G，输出是G上所有顶点的互逆拓扑序号。第1行首先调用Tarjan算法将G中的强连通分量压缩成超级顶点。第2～3行分别调用construct方法建立拓扑序号。

在算法2的construct方法中，第1行将入度为0的顶点按照特定的顺序入栈S，第2行设置一个计数器topNum，用来记录每个顶点的处理顺序。第3行当栈S不为空时，执行第4～10行的操作。第4行先弹出栈首顶点v，并在第5行将顶点v的拓扑序号设置为topNum，同时第6行更新topNum。第7～10行按照特定的顺序处理顶点v的所有出邻居，将其入度均做减一处理，如果减后的入度为0，则将该出邻居顶点入栈。

对于在同一个强连通分量中的每个顶点，各顶点的互逆拓扑序号都等于相应顶点所在的超级顶点的互逆拓扑序号。Tarjan算法和construct方法的时间复杂度都为O（m）， 其中m为有向图G的边数，因此整个genTopo方法的时间复杂度为O（m）。

2.2 基于等价顶点的图压缩方法

在1.1节中给出了等价顶点的相关定义。对于任意2个相互等价的顶点u、v，在回答可达性查询时（除查询顶点对为（u，v）这种特殊情况，稍后讨论）可以相互替换。例如当回答从顶点u到顶点w（其中w≠v）的k步可达查询时，可以替换成从顶点v到顶点w的k步可达查询。

根据该特性，可以实现基于等价顶点的图压缩算法。具体的做法是对于互为等价顶点的一组顶点，只保留其中的一个顶点，同时删除与该顶点等价的其他顶点。当需要回答涉及被删除顶点的k步可达查询信息时，可以通过与查询顶点等价的那个保留顶点来判断可达性。在对图建立2-hop索引之前，通过先对图进行基于等价顶点的图压缩，能有效减小图的规模，从而降低构建索引的时间和索引大小。

本文采用文献[14]中提出的基于分治思想的求解等价顶点方法。该方法的基本思路是首先将顶点集V中的所有顶点视为可能相互等价的，再将集合V分成2个集合，这2个集合中的顶点可能互相等价，但不同集合中的顶点不可能等价。接下来继续对2个集合进行类似的分割，直到每个集合都无法再继续分割下去。最后每个集合中存储的顶点都是相互等价的，而集合之间的顶点是不可能等价的，该算法的时间复杂度是O（m），其中m是图中边的个数。

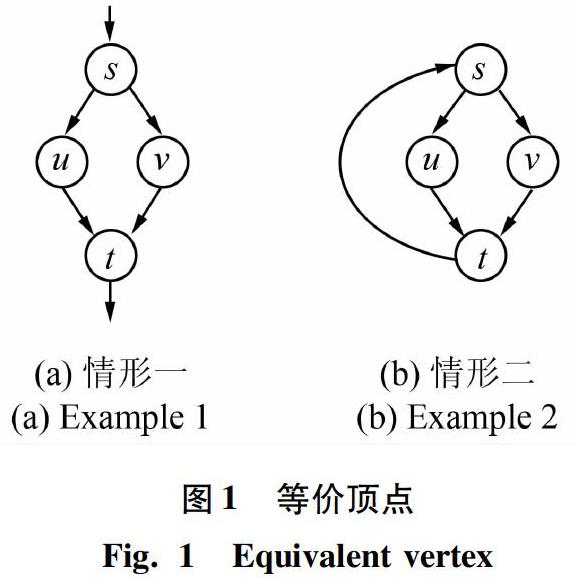
对于2个等价顶点u、v，当查询顶点对为（u，v）时，根据顶点u和顶点v是否位于同一个强连通分量中，会存在2种不同的情况，具体如图1所示。在图1（a）中，即顶点u和顶点v不在同一个SCC并且顶点u和顶点v互为等价顶点，此时顶点u必然不可达顶点v、并且顶点v也不可达顶点u，因此查询结果返回FALSE。在图1（b）中，顶点u和顶点v位于同一个SCC、并且顶点u和顶点v互为等价顶点，则u和v可能是k步可达的（取决于k值是否大于或等于这2个顶点之间的最短路径长度），此时可能就需要通过遍历或者额外的索引来处理这种特殊情况。为了处理这种不常见但又确实存在的查询，导致每一次回答查询时都要进行额外的判断，这显然是十分繁琐又低效的操作。

为了解决该问题，本文提出了一种新的策略，对于不在同一个SCC中的等价顶点，将对其进行压缩操作。而对于处于同一个SCC中的等价顶点，则将其视为不等价的，因此无需进行压缩，等价顶点之间的k步可达查询可以直接通过建立的2-hop标签回答。该策略能有效地避免在这种特殊条件下的冗长而低效的条件分支判断以及遍历图的操作。

2.3 查询方法

算法3给出了在2种优化方法下的PLL算法的查询方法，设计代码依次展开如下。

算法3 query（u，v，k）

输入：源顶点u，目标顶点v，查询距离k

输出：TRUE/FALSE

1 if Xu > Xv or Yu > Yv

2 return FALSE

3 ue ← Eu， ve ← Ev

4 if ue = ve

5 return FALSE

6 ui ← 0， vi ← 0

7 while ui < Lout（ue）.size and vi < Lin（ve）.size

8 hu = Lout（ue）[ui].hop， hv = Lin（ve）[vi].hop

9 du = Lout（ue）[ui].dist， dv = Lin（ve）[vi].dist

10 if hu = hv do

11 if du + dv <= k do

12 return TRUE

13 else

14 ui ← ui + 1， vi ← vi + 1

15 else if hu < hv do

16 ui ← ui + 1

17 else

18 vi ← vi + 1

19 return FLASE

算法3中，第1行先判斷顶点u的拓扑序号X是否大于顶点v的拓扑序号X以及顶点u的拓扑序号Y是否大于顶点v的拓扑序号Y。如果任意一个条件成立，表明顶点u不可达顶点v，因此第2行直接返回FALSE。第3行将顶点u和顶点v转换成对应的等价顶点ue和ve。数组E保存了每个顶点与其对应的等价顶点的关系，该数组由2.2节中所描述的方法求出。第4行如果转换后的等价顶点相等，则查询结果返回FALSE。否则第6～19行通过PLL算法构建的2-hop标签来回答查询。

3 实验分析

3.1 实验环境

本文实验中所使用的硬件平台为Intel（R）Core（TM） i5-4200M @ 2.5GHz CPU，16G双通道内存，操作系统为Ubuntu 18.04.3 LTS。本次实验算法采用C++语言实现，并且查询距离k均取值为10。实验首先比较了PLL算法和PLL算法在分别使用2种优化算法的情况下的索引构造时间、索引大小以及查询时间。随后比较了PLL算法与同时使用2种优化算法的索引构造时间、索引大小以及查询时间。

3.2 数据集

本次研究中所使用的10个数据集见表1。这10个数据集都来自斯坦福大型网络数据集（snap.stanford.edu/data/）。这些图数据集都是有向有环图，表1中标注了每个数据集的顶点数V以及边数E。本文将顶点数大于100000的数据集称为大数据集，因此本次实验中共有5个大数据集以及5个小数据集。本次实验使用的查询集大小为1000000，其中可达顶点对和不可达顶点对的比例为1：1。

3.3 性能比较分析

3.3.1 2种优化技术的比较

PLL算法和PLL算法在分别使用了2种优化方法之后的索引大小见表2。从表2中可以看到，互逆拓扑序号所需的存储空间最多，因为需要额外的2个整型值来存储拓扑序号（即PLL+Topo）。其次是PLL算法，最优的是使用了基于等价顶点压缩的PLL算法（即PLL+GC），因为仅在部分点上建立2-hop索引，从而具有最小的索引大小。

PLL算法和PLL算法在分别使用了2种优化方法之后的索引构造时间见表3。从表3中可以得到与在索引大小中类似的结论，由于需要额外计算2个互逆拓扑序号，因此PLL+Topo的时间开销最多，但由于求解拓扑序号是线性时间复杂度，因此差距并不明显。其次，虽然PLL+GC方法花费了线性时间来计算等价顶点，但是由于进行了图压缩，因此整个索引构造时间相较于PLL算法减少了。

PLL算法和PLL算法在分别使用了2种优化方法之后的查询时间见表4。其中，查询距离k取10。从表4中可以看出在应用了互逆拓扑序号后的查询效率有了明显的提升，在一些数据集上有2～3倍左右的提升。PLL算法在回答不可达查询时的时间消耗要大于回答可达的查询顶点对所花费的时间，而互逆拓扑序号能在O（1）的时间内回答绝大部分的不可达查询，因此提高了查询的效率。对于PLL+GC方法来说，由于进行了图压缩，因此建立的索引大小更小，从而使得查询时需要遍历的hop顶点数更少，因此也在一定程度上提高了查询效率。

3.3.2 PLL算法与PLL-O方法的比较

PLL算法和PLL算法同时应用了2种优化方法（即PLL-O）之后的索引大小见表5。从表5中可以看出在绝大多数的数据集上，PLL-O方法的索引大小要优于PLL算法。只有在极个别图上（如HepTh），图压缩方法对索引大小带来的收益没能抵消2个拓扑号带来的空间开销，此时PLL-O方法的索引规模会略大于PLL算法。

PLL算法和PLL算法同时应用了2种优化方法之后的索引构造时间见表6。由于综合了图压缩方法的优点，PLL-O算法在整体上的性能都优于PLL算法。

PLL算法和PLL算法同时应用了2种优化方法之后的查询时间见表7，其中查询距离k取10。从表7中可以看出PLL-O方法相比于只应用了图压缩的方法的查询效率要高，然而相对于仅应用互逆拓扑序号的方法来说性能差距不大。但综合考虑索引大小以及索引构造时间后，PLL-O方法较PLL算法以及仅使用一种优化方法的PLL方法仍具有较大的优势。

4 结束语

本文针对已有k步可达查询算法存在的不可达查询效率低，索引构造时间长，索引规模大等问题提出了2种优化的方法，分别是基于等价顶点的图压缩方法以及基于互逆拓扑序号的不可达查询优化方法。实验结果表明，在同时应用了这2种算法之后，PLL算法的查询效率、索引大小以及索引构造时间都有了明显的提升。

参考文献

[1]Van HELDEN J， NAIM A， MANCUSO R， et al. Representing and analysing molecular and cellular function using the computer[J]. Biological chemistry， 2000， 381（9-10）： 921-935.

[2]STANN F， HEIDEMANN J. RMST： Reliable data transport in sensor networks[C]//Proceedings of the First IEEE International Workshop on Sensor Network Protocols and Applications. Anchorage，AK， USA：IEEE， 2003： 102-112.

[3]KUMAR R， TUZHILIN A， FALOUTSOS C， et al. Social networks： Looking ahead[C]//Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Las Vegas， USA：ACM， 2008： 1060.

[4]CHEN Yangjun， CHEN Yibin. An efficient algorithm for answering graph reachability queries[C]//2008 IEEE 24th International Conference on Data Engineering. Cancun，Mexico：IEEE， 2008： 893-902.

[5]YU J X， CHENG Jiefeng. Graph reachability queries： A survey[M]//Managing and Mining Graph Data. Boston， MA：Springer， 2010： 181-215.

[6]CHENG J， HUANG Silu， WU Huanhuan， et al. TF-Label： A topological-folding labeling scheme for reachability querying in a large graph[C]//Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data. New York：ACM， 2013： 193-204.

[7]WANG H， HE H， YANG J， et al. Dual labeling： Answering graph reachability queries in constant time[C]//22nd International Conference on Data Engineering （ICDE'06）. Atlanta， Georgia：IEEE， 2006： 75.

[8]WEI Hao， YU J X， LU C，et al. Reachability querying： An independent permutation labeling approach[J]. The VLDB Journal， 2018，27：1-26.

[9]YANO Y， AKIBA T， IWATA Y， et al. Fast and scalable reachability queries on graphs by pruned labeling with landmarks and paths[C]//Proceedings of the 22nd ACM International Conference on Information & Knowledge Management. San Francisco， CA，USA：ACM， 2013： 1601-1606.

[10]CHENG J， SHANG Zechao， CHENG Hong， et al. K-reach： Who is in your small world[J]. Proceedings of the VLDB Endowment， 2012， 5（11）： 1292-1303.

[11]BUNDY A， WALLEN L. Breadth-first search [M]// Catalogue of Artificial Intelligence Tools.Symbolic Computation （Artificial Intelligence）. Berlin /Heidelberg： Springer ， 1984：13.

[12]STEIER D M， ANDERSON A P. Depth-first search [M]// Algorithm synthesis： A Comparative Study. US：Springer， 1989：47-62.

[13]YANO Y， AKIBA T， IWATA Y， et al. Fast and scalable reachability queries on graphs by pruned labeling with landmarks and paths[C]//Proceedings of the 22nd ACM international conference on Information & Knowledge Management. San Francisco， CA，USA：ACM， 2013： 1601-1606.

[13]TANG Xian， CHEN Ziyang， LI Kai， et al. Efficient computation of the transitive closure size[J]. Cluster Computing，2019，22： 6517-6527.

[14]ZHOU Junfeng， ZHOU Shijie， YU J X， et al. DAG reduction： Fast answering reachability queries[C]//Proceedings of the 2017 ACM International Conference on Management of Data. Raleigh：ACM， 2017： 375-390.