如何将笛卡儿思想融入高中平面解析几何课堂
侯代忠 苏元美
[摘 要]在新课程理念下,平面解析几何教学应认真挖掘知识背后的数学文化,发展学生数学思维.笛卡儿作为解析几何的创始者,其思路、思想与方法对现代的解析几何影响深远,更是值得我们挖掘.
[关键词]数学思想;笛卡儿;曲线与方程;课堂教学
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2021)17-0014-03
新课程理念下的数学教育,要在数学本质的基础上赋予课堂新的生命力,强调在课堂上发扬数学文化,传承数学精神.教育家米山国藏说过:随着时间的流逝,僵硬的数学知识点与定理会淡忘在人们的脑中,但是在接受数学过程中产生的数学思想、数学方法、数学思维、数学精神和数学情感等会伴随人们一生,并能够将其运用到其他领域中.
解析几何知识作为高中数学的重要组成之一,在高考中也占有着举足轻重的地位,是学生的重点学习板块.解析几何的知识中包含着许多数学思想,也承载了许多历史.了解解析几何的发展史对我们的几何学习有重要的作用.
《求曲线的方程》作为解析几何的起始内容,在教学中教师常常让学生生搬硬套解题的步骤,不过多解释缘由,从而忽略了一些能很好地渗透数学思想、数学素养、数学情感的好课.本文谈谈如何将笛卡儿思想融入高中平面解析几何课堂.
一、笛卡儿的解析几何思路
法国著名数学家笛卡儿是解析几何的创始人之一.在笛卡儿创立解析几何之前,几何和代数这两个学科早已独立发展起来了,但是却没有交集.当时笛卡儿认为,欧几里得几何太过于依赖图形,在证明过程中过分强调技巧性,过于抽象,对于想象力的要求较高;代数学却是单纯的计算,机械地进行法则和公式的运用,过于死板,不利于思维的发展.
笛卡儿看到了几何的直观性与代数的简便性,他结合了两种领域的优势,创造性地把几何和代数结合起来,也就是“数形结合”思想.此后,数学进入了变量数学阶段,开辟了变量数学,为今后的黎曼几何奠定了基础.笛卡儿曾说过:“我要改革这个局面,把抽象的几何,变成那些不需要去思考太多几何逻辑仅用于练习思想的问题,这样做也是为了更好地研究几何.”
笛卡儿解析几何的基本思路包括:
(1)引入坐標观念,指出平面上的点和实数对(x,y)的对应关系;
(2)利用坐标法,加入极限思想.坐标上的点都可以表示成一个数,当无数个数连接到一起时,便形成了一条曲线,这样就可以用方程去表示曲线;
(3)提出了用方程关系表示曲线的思想,具有同种关系的点,就可用一个方程表示;
(4)找到图形中已知几何图形与未知几何图形之间的等量关系,将其用代数形式表示,用已知的量表示未知的量,构造代数方程;
(5)最后通过代数法则求解方程,最终解决几何问题.
研究笛卡儿创立解析几何的历程,我们可以得到:数学思想——数形结合、特殊到一般;数学方法——变量代替不变量;数学原理——映射原理.
二、《求曲线的方程》中蕴含的解析几何因素
曲线和方程是解析几何中的核心概念.研究曲线与方程的目的是用代数的形式表示曲线的几何特征,并通过代数运算法则处理相关的等量关系,进而利用代数法则去求解,从代数的结论得出相应的几何性质.学会求曲线的方程是研究几何性质的基础与关键,即利用映射原理,将曲线上的点与方程上的解一一对应.曲线上的所有点构成集合,也就是一个方程.“数形结合”与“由特殊到一般”等是整个解析几何的重要数学思想.
目前的教学与学习上侧重于机械的算法训练,忽视了很多几何的特征.笛卡儿创立的对几何简约处理的解析几何,现代学生并没有感受到其科学价值与文化地位.一味的机械计算,又偏离了高中解析几何的课标指引,同时也违背了笛卡儿创立的初衷.
本节通过笛卡儿思想由来的渗透,体会数学的本质,加深学生对数学中的代数方法的认识,巩固求曲线的方程步骤的应用,感悟数学思想.
三、将笛卡儿思想融入解析几何课堂的策略
1.挖掘知识深度
每个知识点的背后都隐藏着独有的思想方法与逻辑思维,而这个知识的历史是数学发展过程的记录,记载了知识的发生和经过,记载了数学家研究成功与失败的过程,其中蕴含着数学思想的传递及数学思维的形成.
历史的研究主要是研究人类的思想,从历史的认识方法论的特征中我们可以了解到,想要研究历史,并不是单纯地了解历史,而是从历史的起点出发,以整体的大观去理解历史,研究其历史思想,并与现实社会结合到一起,在此基础上“再创造”出新的成果.
教师在备课过程中,要对教材进行深入的研究,抓住知识的本质,积极挖掘知识背后的数学文化、思想产生过程.重新整理数学历史材料,提炼出其思想方法,与数学知识结合在一起,为课堂教学做好充分的准备.
课前可以做以下步骤:
(1)挖掘.可以从历史中挖掘出数学逻辑思维、思想方法的文化内涵.
(2)转化.将历史素材转为数学材料,研究解析几何的教学策略.
(3)联系.将课堂及现实社会联系起来.
例如,高中解析几何就是笛卡儿所创立的解析几何,教师在准备这个章节时可以从笛卡儿的创立的心境、环境、思维过程、思想方法和克服困难等去进行课堂各方面的渗透.
2.拓展知识广度
知识的数学史材料包含着知识的思想方法,将数学思想融入课堂的途径可以参考数学史融入数学课堂的途径,使得课堂有趣、丰富起来,让学生在“再经历”的过程中,培养学生的创造性思维能力,同时还能学习数学家刻苦钻研的精神.
对于将数学史材料渗透到数学课堂中,汪晓勤提出了四种方法:附加式、复制式、顺应式、重构式.附加式与复制式是直接应用,较为简单.而顺应式与重构式则是较为高级的渗透方式.重构则是“再创造”知识发生的过程,让学生置身于知识产生的过程,去感悟思想的形成与方法的建构,体会科学家在探索过程中的困难,再感受解决困难时思想发生的过程.
教师可根据不同的课型,选择适当的方式进行教学.
例如,以一个实际问题开启课堂.有一个半径是1米的圆形铁圈,有一根木棍连着圆上的一个动点和距离圆外3米的点,有一只老鼠在木棍上的中点,求老鼠移动的轨迹.
用一个实际题目,设置困难,幻想自己是笛卡儿,如何去解决这个困难?
引导学生思考:老鼠移动的轨迹,就是老鼠的各个脚步汇聚起来的点.将老鼠的各个脚步看成一些点,这些点的集合就是一条线.那么怎么去找到这样的一条线呢?这样的一个中点怎么可以和前面的信息搭建起联系呢?
教师可以切换回历史,当时的笛卡儿和大家也有一样的困扰,这样的问题用纯几何的方法去解决,难度似乎有点大.他为了使问题解决得更快捷,为了能够表示这样的位置,创造出了“笛卡儿坐标系”.他将几何图形搬到“笛卡儿坐标系”中,将“数”与“形”完美地结合在了一起.我们来看看题目有了怎么样的变化?
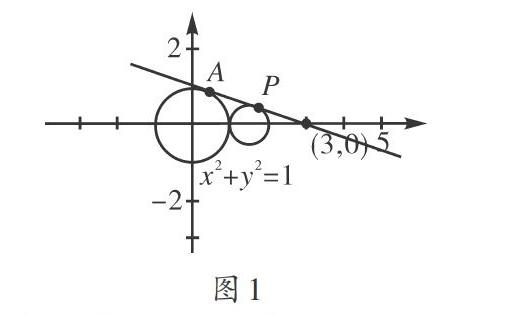
如图1,动点A在圆[x2+y2=1]上移动时,它与定点(3,0)的连线的中点P的轨迹方程是什么?
在这里引导学生用代数的经验去完成题目,进行总结,并展示笛卡儿的思路,进行对比,去感受笛卡儿的解析几何给我们现代生活带来的便利,并学习笛卡儿的创新精神.
3.提升知识高度
在教学之后,教师可升华课堂知识,将知识的传授提升到思想方法的渗透,将理性课堂提升到人文情怀的境界,将知识的学习提升到传承数学精神的层次.教师要善于发现与总结,要将课堂与数学材料的人文情怀与数学精神结合到一起,引导学生从理性思考跨越到感性精神上.
例如,在《求曲线的方程》的课程结尾,可以以下一段话总结,提升课堂的高度.
在今天的这一堂课里,我们“再次经历”了当年笛卡儿的经历,也遇到了同样的困难;我们感受到了数学家的数学思想,感受到了他们的奋斗精神.虽然我们不能完完全全重走他们当年的道路,但是思想能够产生思想,精神能够影响精神.因此,我们要从他的思想中汲取有价值的营养,融入我们新的思路,我们要站在巨人的肩膀上,再创辉煌!
处于现代社会的我们不可能完完全全重走数学家所经过的路程,但是我们也不能因此冷冻历史,而应该让历史鲜活起来,汲取其中的精华.教师作为教育的领路人,应注重在课堂中渗透数学文化,让学生在感受知识的创造过程中,促进思维的发展,领悟数学精神.
[ 参 考 文 献 ]
[1] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[S].北京:人民教育出版社,2018.
[2] 杨懿荔.从数学史视角探究“曲线与方程”教学难点的成因及克服策略[J].上海中学数学,2018(5):3-7.
[3] 李铁安. 基于笛卡儿数学思想的高中解析几何教学策略研究[D].重庆:西南大学,2007.
[4] 宋欣然. 新课标下高中平面解析几何教学策略研究[D].延吉:延边大学,2019.
[5] 国佳.高中新课程“数学史选講”应讲些什么:以平面解析几何产生为例[J].中学数学杂志,2008(7):14-15.
[6] 徐德明. 高中解析几何知识中数学思想方法的教学策略研究[D].哈尔滨:哈尔滨师范大学,2019.
[7] 丁彬.数学史的方法与中学数学教学的融合[J].数学学习与研究,2019(2):61-62.
[8] 王环. 数学史融入初中数学教学现状及策略研究[D].信阳:信阳师范学院,2019.
[9] 许苗.数学史与初中数学新课引入的应用[J].数学学习与研究,2018(3):63.
[10] M.克莱因.西方文化中的数学[M].上海:复旦大学出版社,2004.
(责任编辑 黄桂坚)

