基于CATIA-DMU四连杆悬架不同运动副仿真对比研究

王永卫，韩权武

（北京汽车股份有限公司汽车研究院，北京 101300）

1 概述

本文以某车辆上所采用的四连杆后悬架为研究对象，对空间四连杆机构进行自由度分析，运用CATIA-DMU模块建立四连杆悬架的运动仿真模型，通过对悬架的不同约束进行仿真，对比轮心点间隙误差，结合实际悬架运动方式，确认较合适的四连杆悬架DMU运动仿真校核。

2 四连杆悬架自由度分析[1-2]

空间连杆机构常用的运动副类型有转动副、圆柱副、移动副、球面副、螺旋副、平面副、曲面副等。

自由度为f＝1、2、3、4、5的运动副，相应地称为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ类运动副；第i类运动副允许i个相对自由度，同时也就有Ci=6-i个约束度。

一般空间机构自由度计算公式分为以下两类。

2.1 空间机构单封闭环自由度的公式

空间机构单封闭环自由度的公式为：

式（1）中：F为机构自由度；m为各构件在运动时所受到的公共约束数；n为机构活动构件数；p为运动副的级别，由运动副所产生的约束数来决定；fi为机构i类运动副数量。

2.2 开链机构的自由度计算公式

开链机构的自由度计算公式为：

空间机构不含公共约束的自由度的计算公式为：

式（3）中：n-1为可动构件数；P1～P5为I～V级运动副的数目。

3 四连杆悬架DMU仿真模型建立

四连杆后悬架的结构如图l所示。CATIA-DMU仿真模块中，悬架硬点设置点、线、面元素，建立运动副，对于四连杆悬架弹性元件衬套简化为刚体，不考虑弹性变形。

图1 四连杆悬架结构图

悬架运动建立轮心点上、下跳模拟实车运动，需要对轮心处进行驱动，建立驱动副如图2所示。后副车架总成为固定座基础，在靠近轮心外侧处建立一条平行整车Z向直线1，过该直线平行整车坐标平面YZ面1；再新建一个PART作为中间传递运动副，做出平行整车Z向直线2，过该直线平行整车YZ面2，同时过轮心做垂直直线2的XY平面2，后副车架与PART建立的面和线运动副滑动副，并作为驱动；过轮心面与轮心点建立点曲面运动副。设置驱动行程为轮心上、下跳行程（﹣62 mm，130 mm）。

图2 驱动副建立示意图

四连杆悬架拖曳臂运动副建立方案1如图3所示。从图3中可看出，若相关四连杆杆系与后副车架连接为U型结合，与转向节连接为球面结合，拖曳臂与转向节固联，与车身采用球绞结合。按照公式（3）中，W=﹣1，约束过多，无法进行运动。与DMU仿真报错提示“机械命令过多”一致，因此，需要对某杆件进行约束放开，保证自由度为0。以下是建立两种放开不同点约束的方法。

3.1 托曳臂衬套中心设置点曲线运动副

图3 中，托曳臂衬套中心在后副车架数模中建立衬套轴线，建立点曲线结合，托曳臂一端与转向节固联，后前束调连杆与后副车架建立通用结合，与后转向节建立球面结合。

图3 四连杆悬架拖曳臂运动副建立方案1

3.2 后前束调整杆内点设置点曲线运动副

四连杆悬架后调整杆运动副建立方案2如图4所示。图4中，托曳臂衬套中心在后副车架数模中建立衬套中心点，两者球面结合，与转向节固联结合；后前束调整杆内点中心点处后副车架数模中建立一条水平线，后前束调整杆与后副车架设置点曲线结合，与转向节通用结合。

图4 四连杆悬架后调整杆运动副建立方案2

以上两种建立不同运动副方法完成后，建立机械运动1和机械运动2，进行仿真模拟。

4 轮心点运动仿真对比

对比以下轮心点运动轨迹位移，比较两者在整车坐标系X、Y、Z方向位移的差异，分别如图5、图6、图7所示。

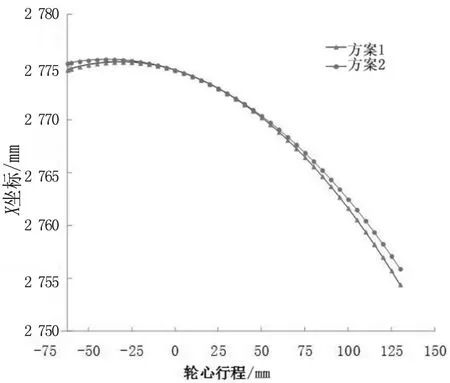
图5 轮心在X向位移对比曲线

图6 轮心在Y向位移对比曲线

图7 轮心在Z向位移对比曲线

方案1和方案2轮心行程（﹣62 mm，130 mm），X向两者差值在1.5 mm以内；Y向两者差值在1.2 mm以内；Z向运动轨迹重合。方案1和方案2轮心在相同悬架行程范围内误差量在整个间隙校核过程中较小，基本忽略，两者不同约束运动副建立不影响间隙校核。

拖曳臂衬套轴向刚度曲线如图8所示。在实际过程中，方案2保持拖曳臂衬套不动，但实际托曳臂衬套属于大衬套，相关衬套刚度比后调整连杆衬套刚度各向较小，托曳臂衬套在X、Y、Z运动幅度较大。放开拖曳臂衬套中心点与实际受力情况分析：拖曳臂衬套在实际各种载荷工况下，提取载荷力，纵向冲击2.0 g中拖曳臂衬套Y向受力最大，本开发车型载荷约930 N，方向朝整车中心面；图8中，拖曳臂衬套轴向刚度取值Y向约5 mm左右，方案1拖曳臂衬套中心运动轨迹Y向朝整车中心面运动量有7 mm，拖曳臂衬套设置点曲线运动副产生方向与实际衬套轴向受力方向一致。方案1托曳臂衬套运动更符合实际运动。

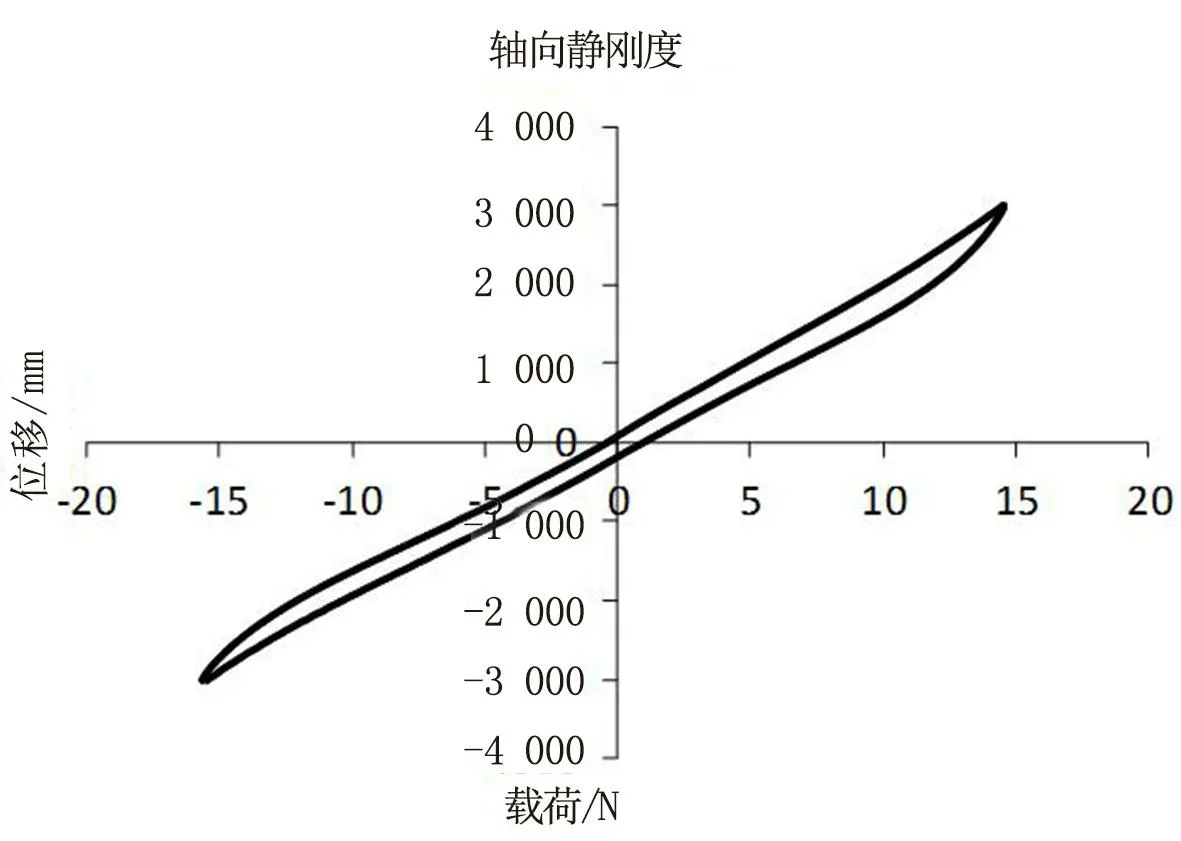
图8 拖曳臂衬套轴向刚度曲线

5 结束语

以上对比分析，CATIA-DMU校核四连杆运动，杆系运动副建立方式不同，但两者产生间隙误差较小，都可应用；实际运动符合情况不考虑衬套弹性变形，拖曳臂衬套设置点曲线运动副约束，更符合实际运动情况，有利于悬架间隙校核。