基于未确知数的纳污能力计算研究

余 正，陈 娟

（1.河北省水利规划设计研究院有限公司，石家庄 050021；2.珠江水利科学研究院，广州 510611；3.水利部珠江河口动力学及伴生过程调控重点实验室，广州 510611）

纳污能力的计算是落实水资源管理制度的一项重要工作。 目前，水域纳污能力计算大多数是针对确定信息下纳污能力计算［1-5］，对信息不确定性研究相对较少［6］。 本文通过未确知数学运算对未确知信息下水域纳污能力进行处理，为水域纳污能力计算提供参考。

1 未确知数理论

1.1 未确知数定义

设未知数A=［（x1，xn），ϕ（x）］，其中

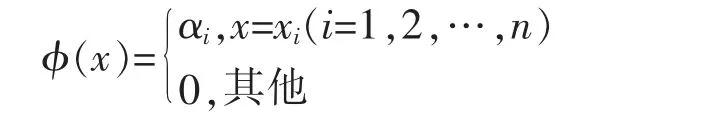
则称闭区间（x1，xn）与函数F（x）构成分布型未确知数，记作{（x1，xn），F（x）}。称a，（x1，xn）和F（x）分别为该分布型未确知数的总可信度、分布区间和可信度分布函数。

1.2 未确知数运算

设{xi}（i=1，2，…，n），{yj}（j=1，2，…，m）分别为未确知数A、B的可能值序列，f（xi）（i=1，2，…，n），g（yj）（j=1，2，…，m）分别为A，B可信度序列。 则

称为A与B的可信度积矩阵。

其中A与B可能和矩阵中第i行第j列元素（xi+yj）与可信度积矩阵中的第i行第j列元素（f（xi）g（yj））相对应。

A与B可能和矩阵中元素按小至大顺序排列z1，z2，…，zk，其中相同元素算1个，A与B可信度积矩阵中zi（i=1，2，…，k）的相应元素为r1，r2，…，rk。 若zi在A与B可能和矩阵有l个不同位置，则ri表示l个相同元素在A与B可信度积矩阵中对应元素之和。

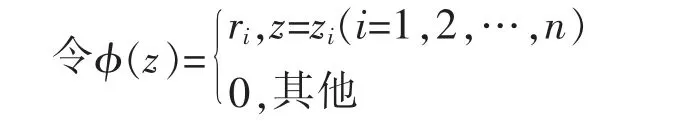
称未确知数［（z1，zl），ϕ（z）］为A与B的和，记作A+B。

将运算中A+B中“+”改为“-”、“×”、“÷”，即可变为可能值差矩阵、可能值积矩阵、可能值商矩阵，其他一切不变。 对于“÷”，要求yj的区间中不能为0（j=1，2，…，m）。

2 纳污能力未确知数学模型的建立

本研究以污染物在横断面上均匀混合的一维河流模型为例，纳污能力计算公式如下：

式中 M为水域纳污能力（g/s）；Cs为水质目标浓度值（mg/L）；C0为初始断面的污染物浓度 （mg/L）；K为污染物综合衰减系数（1/s）；L沿河段的纵向距离（m）；Q为初始断面的入流流量（m3/s）；u为设计流量下的河道断面的平均速度（m/s）。

若令Q、u为未确知数，根据未确知数定义，可将式（1）表示为：

式中 Cs，C0，K，L为实数，符号意义同上；{（x1，xn），u（x）}为流速（m/s）；{（y1，ym），Q（y）}为初始断面的入流流量（m3/s）。 由于引入了未确知数，纳污能力M不再是一个确定值。这里称式（2）为一维河流纳污能力未确知数学模型。同理，可将此方法扩展至一维河流纳污能力数学模型其他参数，如C0，K；也可扩展至纳污能力计算常用的零维模型及二维模型。

通过未确知数运算最终能得到纳污能力未确知数M=［（x1，xn），ϕ（x）］，其中

3 实例研究

3.1 河道资料

某河道长L=15km，水质目标Cs=20mg/L，初始断面污染物浓度C0=18mg/L， 污染物综合衰减系数K=1.2×10-6/s。通过对该河道水文资料统计，得到流速u（m/s）；流量Q（m3/s）。 未确知信息为：

3.2 纳污能力及可信度计算

如果A，B，C，D均为实数计算是没有问题的，但当A，B，C，D为未确知数时， 两种方式得出的计算结果不一样。 原因在于C和D中均含有未确知数Q，即C和D是有关联的，不能当成独立的未确知数。

因此，M=A×B，其中

A与B的可能值积矩阵及可信度积矩阵如表1和表2。

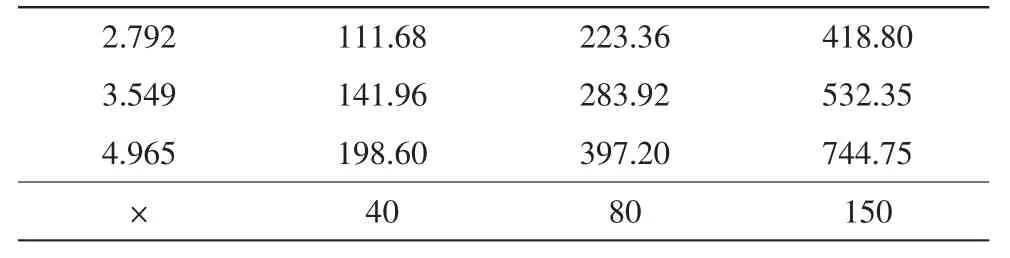
表1 A与B的可能值带边积矩阵

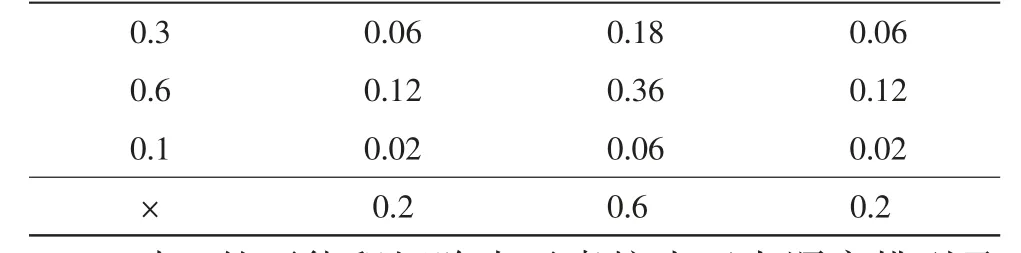
表2 A与B的可信度带边积矩阵

A与B的可能积矩阵中元素按小至大顺序排列及A与B可信度积矩阵中对应元素，得到{（z1，zl），ϕ（z）}。

A×B=［（111.68，744.75），ϕ（z）］={（111.68，744.75），F（z）}

ϕ（z）及F（z）的计算值如表3，即得到该河道纳污能力可能值及相应的可信度分布。

表3 纳污能力可能值及相应的可信度

续表3

3.3 结果分析

由表3可看出， 纳污能力计算结果主要出现在［111.68，744.75］ 区间范围内， 并且在区间［283.92，397.20］内出现的主观可能性最大，相应的区间可信度达到36%，其次在区间［223.36，283.92］内出现的主观可能性也较大，相应的区间可信度为18%。 由此可以看出，运用未确知数进行水域纳污能力计算，不仅能得到水域纳污能力区间值， 还能得到相应的主观可信度。同时，也可求得未确知信息下的纳污能力确定值，这可为决策者提供更丰富、更准确的信息。

目前，我国许多河流、湖（库）存在水文、水质资料较少，信息不全的实际情况，这为未确知数在该领域的应用提供了广阔的发展空间。

4 结语

（1）实例研究表明，运用未确知数进行不确定性信息下的水域纳污能力计算，理论上可行，计算结果可靠，为纳污能力计算提供了一种新方法。

（2）纳污能力未确知数运算中需注意未确知数间的独立性，避免与同一未确知数有关联。