监测信息不完整状态下的大坝整体性态监控方法
姜振翔,陈 辉,陈鲁皖
(南昌工程学院 水利与生态工程学院,江西 南昌 330099)
大坝安全监控是保障大坝安全运行的重要方式[1]。通过在坝体内合理地布置监控仪器、采用适当的方法分析监测资料,有利于找出并处理大坝在服役过程中的薄弱环节,从而降低工程失事风险,为大坝的安全运行提供可靠的技术支持。
目前,对大坝性态的监控主要依靠单测点(局部性态)监控模型实现[1],即建立环境量(如水位、温度、时效)与效应量(如位移、渗流)之间的线性数学模型[2-5],并拟定相应的监控指标[6-8],从而达到监控大坝性态的目的。关于大坝整体性态的监控方法,目前的研究成果相对较少。苏怀智[9]利用重标极差分析法融合多测点测值信息,将Hurst指数作为表征大坝整体性态的指标,通过建立该指数的监控模型达到监控大坝整体性态的目的。Sortis[10]将坝体弹性模量作为表征大坝整体性态的指标,结合有限元模型和位移监测数据反演弹性模量,并根据弹性模量的变化监控大坝整体性态。虞鸿[11]、王少伟[12]利用传统主成分分析(PCA)提取多测点监测信息中的主成分(PC),并将PC作为反映大坝整体性态的依据,建立了PC的监控模型。雷鹏[13]采用变形熵描述大坝整体变形,该值是多测点变形的定性综合,通过定期计算变形熵达到监控大坝整体性态的目的。
这些研究成果为大坝整体性态的监控提供了有益的研究思路,但也存在着一些不足。例如:采用Hurst指数、变形熵等方式难以实现实时监控;同时,监测资料的自动化采集系统容易发生损坏,导致数据缺失,若针对PC进行监控,则可能会影响模型预报精度。因此,在监测信息部分缺失的条件下,大坝整体性态的实时监控方法可以做进一步的研究。
本文采用PPCA处理不完整的大坝多测点监测资料,在保留原始监测信息的基础上,提取表征大坝整体性态的概率主成分(PPC),并建立了PPC的监控模型,可为实时监控大坝整体性态提供参考。
1 研究方法
1.1 PPCA原理
在大坝安全自动化监测系统中,由于仪器损坏等原因,部分测点往往会在不同时间段内存在小部分的数据缺失,导致各测点监测数据不能同步。若采用传统方法建立定量分析模型,则需要对原始数据进行处理,仅保留各测点共有的数据。然而,由于各测点数据缺失的时间段不同,直接删除不同步的数据将损失大量监测信息,不利于大坝整体性态的监控与诊断。PPCA[14-15]则能很好的解决大坝原始监测资料中的数据缺失问题,该算法以测点间的相关关系为基础,通过这种相关关系推算监测资料中的缺失数据,并提取表征大坝整体性态的PPC,从而达到在多测点监测数据中提取关键信息的目的。
设某效应量共有q个测点(即q个原始变量),每个测点包含n次测值,则这些测点测值构成了q×n的矩阵X:
(1)
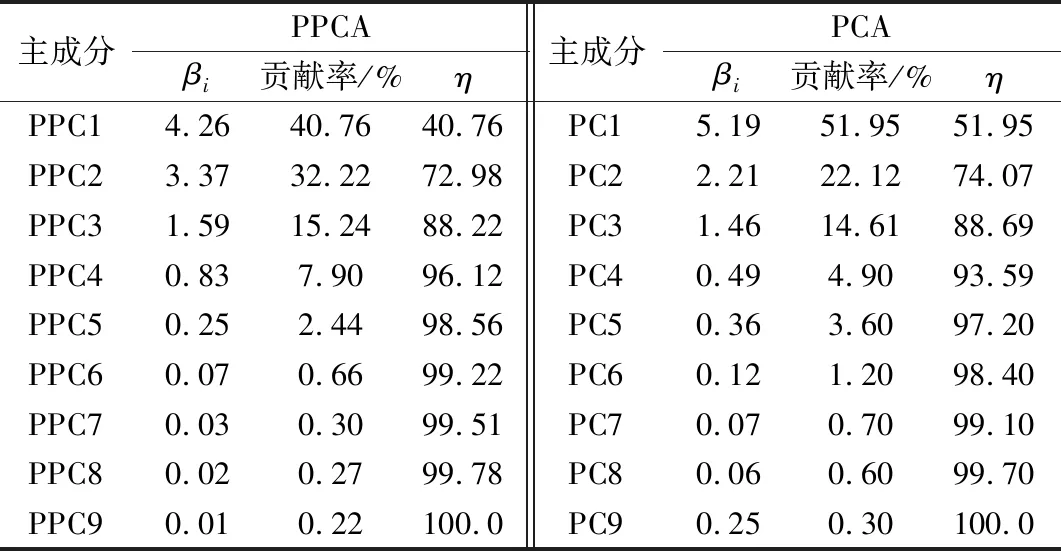
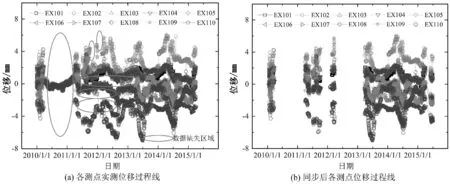
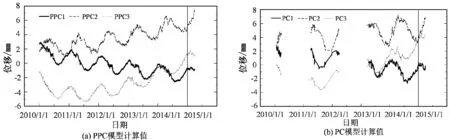
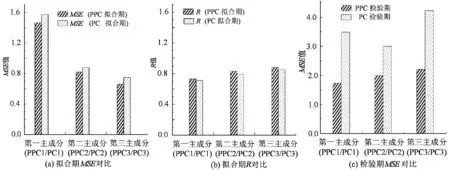
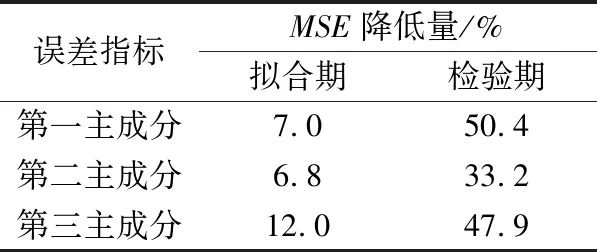
式中Xi为行向量,表示第i个测点的观测数据序列;xij表示第i个测点的第j次观测值。设存在r维(r X=WY+μ+ε, (2) 式中W为q×r阶矩阵,反映了原始变量X与隐含变量Y之间的相关关系;Y服从正态分布,即Y~N(0,I);ε为观测噪声,服从正态分布,记为ε~N(0,σ2I);I为单位矩阵;σ2为观测噪声的方差;μ为样本均值矩阵,μ=[u1,u2,…,uq]T,uj为第j个测点的监测数据平均值。由统计学原理[16],可得: X~N(μ,WWT+σ2I). (3) 若X的信息完整,W可通过对X的协方差矩阵进行奇异值分解直接求出,对应的Y即为PC。若X的信息不完整,则首先应从X中分离出数据缺失的列,将信息完整的列组成矩阵Xexist。对其做奇异值分解,求出Wexist。由于X~N(μ,WWT+σ2I),可构造X的似然函数为 L=ln {p(Y|X,W,μ,σ2)}, (4) 同时构造误差函数: (5) (6) 上式可记为 (7) 式中kij为第i个PPC中第j个原始变量的系数,kij的绝对值越大,Yi与Xj的相关程度就越高,Yi就越能被Xj解释;当kij为正时,Yi与Xj正相关;当kij为负时,Yi与Xj负相关。 当原始变量的个数为q时,最多可以重构q-1个PPC,但这q-1个PPC对原始变量的解释程度是不同的,因此需要从q-1个PPC中提取z个最能描述原始变量特性的PPC。对于z的取值,可根据累计方差贡献率确定: (8) 在大坝安全监测领域,建立位移效应量的监控模型是监测大坝性态的重要方法。已有的坝工知识和工程经验表明,大坝的单测点位移效应量受水位、温度、时效等环境量的共同影响[1]。由式可知,PPCA的实质是对各测点的原始监测数据进行线性变换,所得的PPC为原始变量的加权线性组合,因此PPC仍为水位、温度、时效的函数。因此,PPC的监控模型可表达为 (9) 万安水利枢纽位于江西省赣江中游万安县境内,由混凝土重力坝、土石坝和通航建筑物(船闸)组成。其中混凝土重力坝坝顶高程104 m,最大坝高46.04 m,布置了较为完善的变形监测系统。本文以溢流坝(表孔泄流段)基础廊道(约64 m高程)内EX1引张线的10个测点(EX101~EX110)为例,以2010年1月1日至2015年3月31日作为分析时段,讨论该时段内,在部分测点监测数据缺失状态下PPC的提取、PPC监控模型。EX1引张线各测点布置如图 1所示。 图1 万安水利枢纽EX1引张线测点布置示意图 在分析时段内,各测点的自动化监测系统每天记录一次位移读数。因此,在理论上,各测点均应存在1915次监测数据。然而,由于数据采集模块在部分时段损坏,导致所有测点数据在该时段内缺失,共93次;剩余1822次监测数据中,受引张线仪、电缆损坏等因素的影响,不同测点在不同时段内均存在一定的测值缺失。图2(a)为各测点在分析时段内的原始位移过程线。若采用传统方法提取主成分,需要将监测资料进行同步处理,即仅保留各测点监测数据均存在的时段。同步后,共剩余1009组数据,监测信息约损失45%,由此得到图2(b)。 根据式(4)~(7),采用PPCA分析图2(a)过程线。建立原始监测信息的似然函数,采用最大期望算法进行求解,令迭代误差Err≤10E-4时停止迭代。同时,为说明PPCA在提取主成分方面的有效性,采用传统的PCA分析图2(b)过程线作为参照。表1列出了分别采用PPCA和PCA方法提取的主成分特征根βi(i=1,2,…,9)、相应的贡献率以及累计贡献率η。由表可知,采用PPCA和PCA得到的主成分,虽然βi值、贡献率、η值存在差异,但前三个主成分的η值分别为88.22%和88.69%,大于85%,可以认为PPC1、PPC2、PPC3和PC1、PC2、PC3均能较好的解释原始监测信息,即可以采用前三个主成分代替EX1中的10个原始测点。 表1 主成分分析结果 图2 各测点原始过程线与同步后过程线 综上,PPCA和PCA提取主成分的有效性相近,但由于PPCA的分析对象为不完整的监测数据;PCA的分析对象为同步后的监测数据,使得PPC与PC的βi值、贡献率、η值不同。 根据式计算PPC1、PPC2、PPC3的表达式系数,同时计算PC1、PC2、PC3的表达式系数,如表2所示。 表2 PPC和PC系数 由表2可知,采用PPCA和PCA得到的主成分对原始变量的解释程度相近:在PPC1和PC1中,EX103、EX104、EX105、EX106、EX107、EX108测点的系数较高,表明第一主成分主要解释了这些测点测值的变化规律;类似的,PPC2和PC2主要解释了EX101和EX102测点测值的变化;PPC3和PC3主要解释了EX109和EX110测点测值的变化。得到PPC1,PPC2,PPC3的过程线如图3(a)所示;PC1,PC2,PC3的过程线如图3(b)所示。对比图3(a)和图3(b)可知:PPCA与PCA的共性在于,EX1引张线的所有测点,其测值在前三个主成分中均得到了解释,经过分析后,变量数从原始的10个变量降为3个,提高了大坝整体性态的监控能力。但应注意到,鉴于PPCA能够推算缺失数据,PPC具有连续、完整的过程线。 图3 PPC与PC过程线 通常,分析时段被划分为拟合期和检验期。在拟合期内,通过逐步回归法训练水位、温度、时效等环境量与位移之间的关系,建立监控模型;在检验期内,根据误差指标评价监控模型的预报精度。本文将2010年1月1日至2014年12月31日作为拟合期,利用该时间段内的监测数据(共1732组)建立监控模型,由式训练该时间段内的环境量与主成分实测值,得到监控模型;将2015年1月1日至2015年3月31日作为检验期,利用该时间段内监测数据(共90组)检验模型的预报精度。 将拟合期与检验期内的环境量代入监控模型,可得各PPC的监控模型计算值,由此绘制PPC1、PPC2、PPC3和PC1、PC2、PC3在分析时段内监控模型计算值过程线,如图 4(a)和图 4(b)。 图4 拟合期和检验期过程线 由图4可知,与PC的监控模型计算值过程线相比,PPC的监控模型计算值过程线更加平滑,且周期性和规律性较强。为更好地对比两者精度,采用均方误差MSE和复相关系数R作为评价模型质量的指标。其中,MSE反映了模型计算值与实测值在整体上的偏差程度,MSE越小,表明在整体上,模型计算值越接近实测值;R值反映了在拟合期内模型计算值与实测值在整体上的相关程度,R值越大,表明在整体上,两者相关程度越高,模型精度更高。MSE与R的计算方法分别为 (10) (11) 图5 PPCA与PPC在拟合与检验期误差指标统计 由图5(a)和图5(b)可知,与PC的监控模型相比,在拟合期,PPC监控模型的MSE略低;R值略高,PPC监控模型的R值在0.74~0.89之间,而PC监控模型的R值在0.71~0.84之间。由图5(c)可知,在检验期,PPC模型MSE明显降低,即表明PPC监控模型的预报精度显著提高。表3统计了各PPC模型在MSE方面的优化量:在拟合期,MSE降低6.8%~12%;在检验期,MSE降低33.2%~50.4%。由此可知,由于PPCA能够利用数据间的相关性补充缺失数据,其过程线更加平滑,有利于提高模型的拟合精度和预报精度;而采用PCA时,由于需要同步数据,损失了约45%的监测信息,不利于监控模型的建立,其精度相对较低。同时需要注意到,在采用PPC和PC方法时,所建模型的计算值与实测值均在每年的高温季节(7月-8月)差值较大,最大可达5.6mm,该时期的差值是MSE的主要来源,而在其他时段的差值较小。其原因在于,在这一时段内,坝前水位较高,且气温较高,大坝位移与水位、温度、时效等环境量之间的关联特征可能表现出线性与非线性耦合,而本文采用了工程中常用的线性算法建立监控模型,导致模型计算值与实测值相差较大。但从总体上看,采用PPCA方法由于能够获得更多的样本,因此在这一时段内,仍然具有较高的精度。 表3 各PPC相对于各PC的MSE优化量 本文研究了在部分监测信息缺失状态下大坝整体性态的监控方法,探讨了PPCA在监测信息不完整时,从多测点监测资料中提取关键信息的有效性,并采用多元回归分析建立了PPC的统计模型,得到以下结论: (1)PPCA能够在大坝安全监测数据部分缺失的状态下,根据数据间的关联特征重构监测序列并提取关键信息,从而能够有效避免采用传统方法时,因需要同步数据而造成的监测信息损失。 (2)PPC过程线较PC过程线平滑,更有利于监控模型的建立。根据PPC建立的监控模型能够实现大坝整体性态的实时监控。算例表明,PPC监控模型的各项误差指标均优于PC监控模型,PPC监控模型在预报阶段的MSE值降低30%以上,模型预报精度显著提高。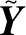
1.2 监控方法
2 工程算例
2.1 工程概况

2.2 PPC的提取


2.3 PPC监控模型
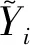
3 结论

