掘进巷道流场结构及粉尘沉降规律相似模拟研究
王 冕
(河南能源义煤集团新义矿业有限公司,河南 洛阳 471800)
煤炭产业是我国的支柱产业之一,2016年以来煤炭产量稳步提升,2019年的煤炭产量高达38.5亿t[1]。而目前煤炭开采主要以井工开采为主,煤炭破碎后生成的粉尘不易扩散,尤其是细小颗粒物会长期悬浮在巷道空气中,通过人的呼吸系统进入肺泡引发尘肺病[2]。近年来我国新增职业病中尘肺病占80%以上[3],因此井下掘进巷道粉尘防治问题引起了广泛关注。
随着计算机技术的发展,越来越多的学者利用数值仿真技术模拟粉尘运移规律[4],为矿井粉尘防治工作的开展提供了依据。REN Tingxiang等[5]为改善落煤仓粉尘污染,基于CFD数值模拟提出了两种可行的粉尘控制方案,一种是对通风系统进行改造用风流稀释可吸入的粉尘颗粒,另一种是采用细水雾降尘器抑制和捕获大部分粉尘颗粒;GENG Fan等[6]基于混合式通风的简化模型,模拟研究了煤巷掘进过程中不同粒径的粉尘颗粒的扩散规律,对粉尘的沉降、回流及其动态分布特性进行了分析;CHENG Weimin等[7]采用CFD-DEM耦合模型和现场实测相结合的方法,对综掘工作面粉尘颗粒的扩散行为进行了研究;YU Haiming等[8]采用相同的模拟方法研究压入式通风条件下综采工作面高浓度粉尘的扩散污染机理,分析了不同尺寸粉尘颗粒的扩散特征;NIE Wen[9-10]、CHENG Weimin[11]等利用FLUENT软件模拟研究了采煤过程中风量变化和多尘源粉尘扩散影响下的巷道粉尘浓度分布规律。除上述数值模拟研究之外,另有不少学者将相似理论应用于分析气固两相流的相关工程问题[12-13]。蒋仲安等[14-15]运用气固两相流理论建立相似准则,通过相似实验研究采掘工作面的通风降尘问题,弥补了现场测试的局限性。
综上所述,掌握风流的特征和粉尘的扩散、聚积、沉降规律是做好粉尘防治工作的前提和关键基础。笔者基于掘进巷道压入式通风系统,采用数值模拟与相似模拟实验相结合的方法,研究压入式通风的流场结构特征,分析风流对粉尘扩散和沉降规律的影响机制。以期为改善工作面环境和优化掘进巷道通风降尘系统提供理论支持。
1 相似模拟实验平台
1.1 相似理论在气固两相流中的应用
气流是粉尘颗粒运动的主要动力,须用气体运动方程和尘粒运动方程相结合来描述掘进巷道内气固两相流动的物理现象。将巷道内空气视为黏性不可压缩流体,对于不可压缩气体的非定常流动[16],其运动方程为:
(1)
式中:ρg为气体密度,kg/m3;vg为气体速度(vg为速度梯度),m/s;m为单位体积上的质量力,m=ρgg,N/m3;p为气体的压力(p为压力梯度),Pa;f为除质量力、气体压力以外的其他作用力矢量,f=μg2vg,且为重力加速度,m/s2;μg为气体黏性系数,N·s/m2。
将粉尘颗粒视为球形,只考虑气固两相相对运动产生的作用力,其运动方程可表述为[16]:
(2)
式中:ds为固体颗粒的直径,m;ρs固体颗粒的密度,kg/m3;CD为阻力系数;vs为固体颗粒的速度,m/s;vr为气固两相的相对速度,即vr=vg-vs。
为使模型实验能反映掘进巷道内气固两相的运动特征,模型需要满足几何相似、动力相似和运动相似等要求。图1为气固两相流相似理论应用图,运用无量纲分析方法对气体运动方程和颗粒运动方程进行分析,其中有量纲的量为ρg、ρs、vg、vr、μg、ds、g、l(几何尺寸的特征长度)、t、p。基本物理量只有质量[M]、长度[L]和时间[T],则根据量纲π定理及单值条件相似,可得出10个相似准则。在进行实际研究过程中,很难保证所有的相似准则都相等,因此根据掘进巷道通风降尘的需要,将这10个相似准则简化为4个准则:斯托克斯准则Stk、颗粒雷诺准则Res、粗糙度准则Δ/D和几何相似准则D/L[17]。
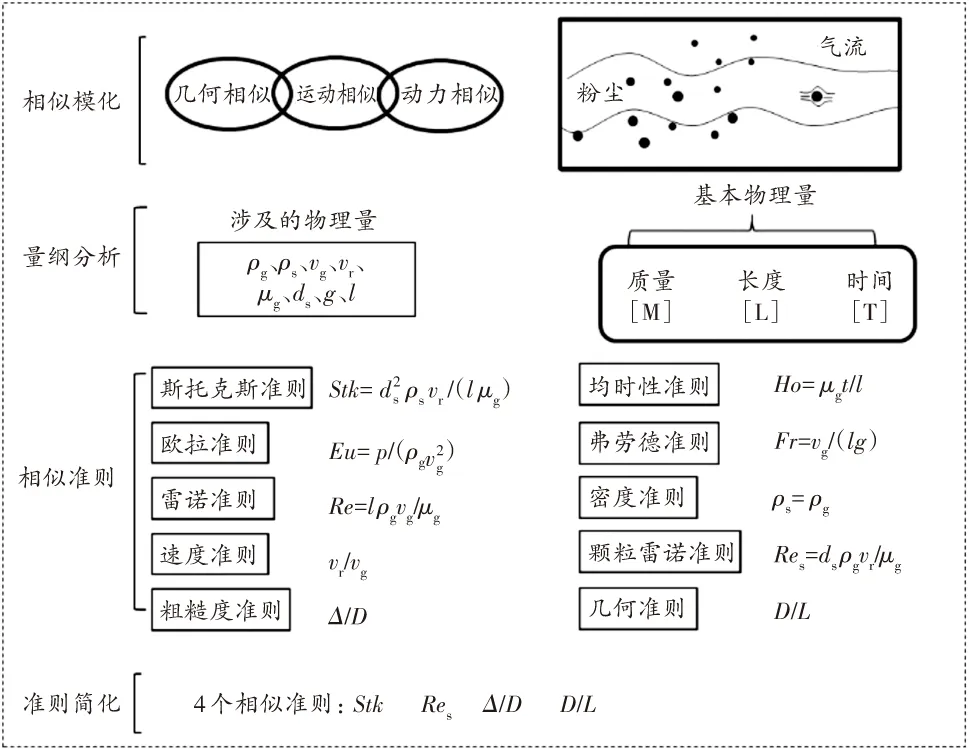
图1 气固两相流相似理论示意图
根据相似理论第一定理,两个相似的现象其同名准则数必定相等[18-19]。几何相似准则Δ/D和D/L易实现相等。由模型与原型的Stk和Res相等,联立方程组可得出模型内风速vgm与原型风速vgy的关系式(下标y表示原型,下标m表示模型)。
(3)
同时应满足流体雷诺数Re>2 300,流体处于完全紊流状态,原型与模型流体均位于第二自模区,保证其动力相似进而保证流体的运动相似。
1.2 掘进巷道相似模拟实验系统
基于以上理论搭建了掘进巷道相似模拟实验平台,如图2和图3所示。
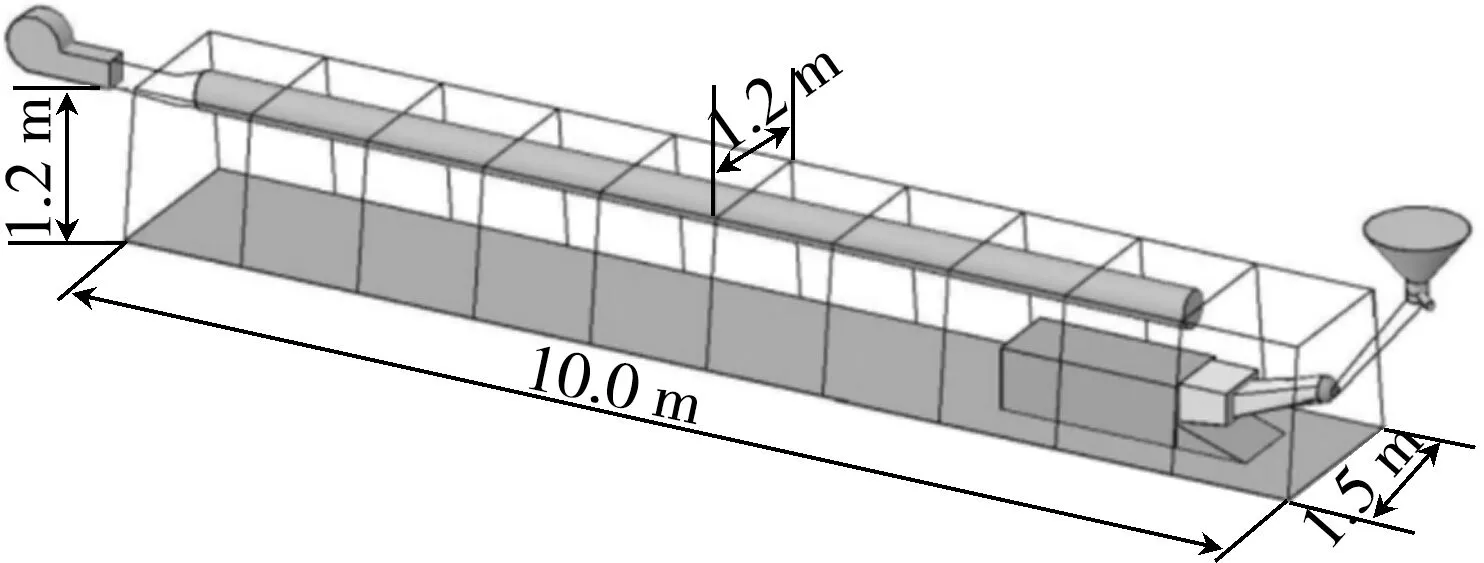
图2 掘进巷道相似模拟模型设计图

a—风机;b—压风筒;c—工作面端头;d—梯形巷道;e—测试孔;f—巷道内部。
模型为10 m长的等腰梯形巷道,梯形截面尺寸为上底长1.2 m、下底长1.5 m、高1.2 m。风筒直径为30 cm,掘进机模型由EBZ120型掘进机简化而来,尺寸为长2.7 m、宽0.6 m、高0.5 m。巷道内同一断面设置9个风速测点(1#~9#),风速测点分布如图4所示。风速测量仪器为热敏式风速仪,如图5所示,仪器精度为0.001 m/s,与传感器相接的探棒可伸缩、弯曲,实验时将探棒穿过巷道壁面的测试孔,通过调整长度和角度测定不同位置的风速。

基于上述几何形状,相关参数可确定如下:认为巷道内空气密度与模型实验气体密度相等,取20 ℃时的空气密度,即ρgy=ρgm=1.205 kg/m3;取巷道原型气体动力黏性系数μgy=2.3×10-5N·s/m2,模型气体动力黏性系数μgm=1.81×10-5N·s/m2;针对上底和高为4 m、下底为5 m的实际梯形巷道,几何尺寸比则为0.3,模型当量直径Dm=1.266 m;掘进巷道的实际平均风速一般为0.25~1.00 m/s,根据式(3)可计算出掘进巷道压入式通风相似模拟实验的平均风速范围。
由以上条件可知:
(4)
(5)
因此,Re>2 300满足实验条件。故模型实验的平均风速控制在0.66~2.62 m/s内。实验过程中风筒风速为30 m/s,则巷道平均风速为1.38 m/s,在上述范围内。
2 数值模型构建
2.1 数值计算控制方程
基于掘进巷道相似模拟实验模型构建数值模拟模型,利用FLUENT软件开展相关模拟研究。模拟采用欧拉—拉格朗日模型对掘进巷道中流场及粉尘运移规律进行计算分析。欧拉—拉格朗日方法将流体处理为连续相,应用牛顿第二定律跟踪求解流场中的粒子运动轨迹,基本控制方程如下[20]:
1)气相连续性方程为:
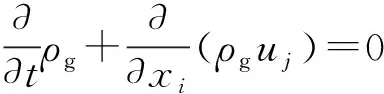
(6)
式中:t为时间;ρg为气体密度;u为时均速度;i、j表示自由坐标系下的方向。
2)动量守恒方程为:
(7)
式中:p为法向应力;τij为切向应力;Fsf为离散颗粒对流体的作用力。
3)气固两相流模式下的Realizek-ε模型方程为:
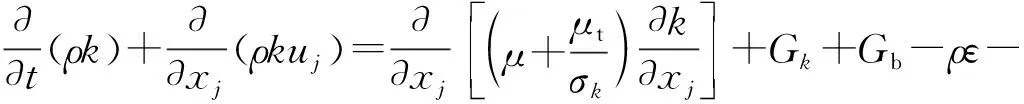
(8)
(9)
式中:k为湍流动能;ε为耗散率;μ为黏度;μt为湍动黏度;Gb为由于浮力产生的湍流动能;Gk为由于平均速度梯度引起的湍动能k的产生相;YM为由于运移和扩散产生的可压缩湍流的波动;σk为与湍动能k对应的普朗特数;Sk为由于颗粒运动引起的湍动能k的产生项;Sε为由于颗粒相而引起的耗散率产生项;S为变形张量;C1、C2、C3为经验常数。
4)根据牛顿第二定律,颗粒项的运动求解方程为:
(10)
(11)
式中:mp为颗粒的质量;vp为颗粒速度;Ffp为连续气体相与颗粒的流体作用力,且Ffp=-Fpf;Ip为颗粒的惯性项;ωp为颗粒旋转的角速度;Mfp为作用于颗粒上总的旋转矩。
2.2 物理模型及参数设置
利用ICEM绘制与相似模拟实验平台等尺寸的物理模型,如图6所示。风筒中心距底板0.75 cm、距工作面端头2 m、距壁面0.07 m。与实验系统相比,综掘机位置、风筒位置及风速设置与实验参数设置相同,而压风机被简化掉,仅保留风筒作为气流来源;为了减少计算负荷,风筒内部的流场不在计算域之内;模型x轴表示巷道宽度,y轴表示巷道高度,z轴表示巷道长度。计算网格主要采用非结构化网格划分,由于掘进机的机身棱角较多,在掘进机附近部位进行相应的网格加密,同时在风筒壁面附近及风筒出口也进行网格加密。网格总数在 1 145 000 左右,平均网格质量达0.745,满足计算精度要求。其中最小网格质量为0.3,最大网格质量达到0.999 5。

图6 掘进巷道物理模型及网格
采用k-ε方程模拟压入式通风的流体相运动,将粉尘看作离散相,采用DPM模型求解,与连续相耦合计算。边界主要包括入口、出口、颗粒喷射源及壁面,边界设置如表1所示。风筒入口即为风流来源,对于入口风速为30 m/s时,其相应的湍流强度为3.03%。由于相似模拟实验巷道外部为大气环境,可将出口设置为出流。

表1 模型边界条件及粉尘源设置
3 压入式通风模拟及实验结果分析
3.1 流场结构对粉尘扩散的影响
为分析压入式通风的流场结构特征对粉尘扩散的影响,从模拟结果中提取了风流的迹线图和粉尘颗粒分布图,如图7所示。

图7 巷道流场结构图
由图7可知,压入式通风的流场结构可分为射流区、射流贴附区、涡流区和回流区。射流区位于风筒出风口前方,如图7中Ⅰ区域,此处风速较大但衰减较快,主要以射流发展为主,流场结构简单;贴附区位于巷道端头附近,如图7中Ⅱ区域,此处风流速度衰减较大,风流方向各异;涡流区主要位于综掘机附近,如图7中Ⅲ区域,由于受到综掘机、巷道壁面空间限制作用及射流区卷吸效应的影响,涡流结构较多;而回流区位于综掘机右侧及后方,如图7中 Ⅳ区域,此处流场结构相对简单,风流流向巷道出口,回风侧风速大于巷道中部及风筒侧的风速,即图中所示高速区和低速区。
射流区是自由射流受到壁面限制而演化形成的;射流贴附区是气流冲击工作面端头后沿壁面贴附运动形成的;涡流区是受高速气流卷吸和受限空间影响形成的;回流区是指向巷道出口方向运动的气流。从图7中不难发现,经壁面折返的气流携带了大量粉尘向巷道后方运移,在综掘机后方逐渐扩散开。可见风流是携带粉尘运移的主要动力,粉尘运动特征和流线特征相契合。而综掘机附近弥散的粉尘颗粒较少,这是由于大颗粒粉尘自身惯性大,可随回流向后运移并沉降,而小颗粒粉尘随机扩散,部分受到涡结构的影响而滞留在工作面前方。
3.2 风速分布对粉尘沉降特征的影响
基于掘进巷道相似模拟实验平台,进行了压入式通风的风速测定和粉尘沉降实验。所选取截面上各个测点的风速测定结果见图8。

图8 风速测定结果
由图8可知,气流速度沿巷道走向整体呈现下降趋势。1.0 m截面的3#和6#测点位于压风筒前方,因此风速尤为偏高。就整体而言,1#、4#、7#测点的风速明显普遍高于相同高度的其他测点。可见在巷道空间内回风侧的风速较高,风筒侧的风速普遍较低,因此,回风流成为携带颗粒运动的主要动力。除1.0 m断面受射流区影响较大外,巷道同一断面中1#、4#、7#测点的风速值均高于其他测点风速值,即回风侧的风速大于巷道中部和风筒侧的风速值,这一规律与数值模拟结果是一致的。
风速分布会影响底板粉尘的沉降特征,为此在巷道底板均匀放置白纸,观察粉尘沉降规律。每隔1 m铺设3个粉尘收集点,横向间隔0.3 m,实验结果和模拟结果如图9所示。

图9 巷道底板粉尘沉积现象
由图9可以看出,巷道内粉尘沉降情况为进风侧沉降量<巷道中部沉降量<巷道回风侧沉降量。在回风侧3~5 m区域出现了大颗粒粉尘堆积沉降的现象,沉降粉尘的粒径随与工作面端头距离的增加而逐渐减小,即从a至e粉尘粒径逐渐减小。其主要原因是随着风速在巷道内的衰减,大颗粒粉尘受重力作用在3~5 m内首先沉降,小粒径粉尘则随着风速的降低缓慢沉降。而巷道前方风速较大,在前方 2 m 范围内粉尘沉降量小。同时,在巷道3 m处,巷道中部粉尘沉降分布较两侧均匀,无明显堆积现象。这主要是由于此处为综掘机正后方,风流自综掘机右侧向后发展时产生绕流,使综掘机后方形成流场低速区。低速气流仅携带小颗粒粉尘经过此处并发生沉降。
上述实验粉尘沉降特征与模拟结果的底板粉尘质量浓度分布基本一致。由于回风侧风速较高,携带粉尘能力较强,因此能够携带多数大颗粒粉尘在回风侧运移并沉降。颗粒较小的粉尘惯性小,随扰动的风流扩散至风筒下方。
3.3 风速分布验证
通过以上分析可发现模拟结果的风速分布特征、粉尘沉降特征与实验结果具有较好的一致性。为进一步确保研究结果的可靠性,选取巷道中距工作面端头1、2、3 m 3个横截面测点的风速对模拟结果进行对比验证。模拟结果与实验结果对比如图10所示。
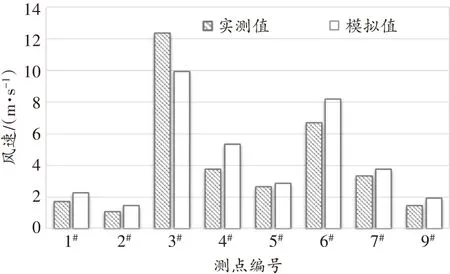
(a)距工作面端头1 m处横截面

(b)距工作面端头2 m处横截面

(c)距工作面端头3 m处横截面
由图10可知,巷道内同一断面各测点数值模拟风速与实验结果变化趋势基本相同,个别测点风速值存在差异,主要是由于实验条件和误差所致,总体数据贴合度较好。
4 结论
1)掘进巷道压入式通风相似模拟实验系统在满足斯托克斯准则、雷诺准则、几何相似准则和粗糙度准则情况下,得出模型的合理平均风速为0.66~2.62 m/s。模型与原型的风速比与几何尺寸、气体密度和黏度相关。
2)掘进巷道在压入式通风条件下流场可分为射流区、射流贴附区、回流区及涡流区。巷道整体回风侧风速较高,是携带粉尘向后运移的主要动力。粉尘在综掘机后方开始发生明显扩散,而综掘机附近的涡流区仅捕获少数的微细粉尘。
3)大部分粉尘沉降发生在回风侧距工作面端头3~5 m区域,均为大颗粒粉尘。随着与工作面端头距离的增加粉尘粒径逐渐减小。由于气流在综掘机后方发生绕流,形成低速区,此处沉降的粉尘颗粒明显较小且底板粉尘沉降量分布均匀,无堆积现象。

