反向时间依赖路网上移动对象的启发式k近邻查询算法
宋力翔,秦小麟
(南京航空航天大学 计算机技术与科学学院,南京 210016)
1 引 言
如今,随着移动设备的发展,在我们的日常生活中越来越普及.由于现有的移动设备通常都装有全球定位系统芯片,用户可以很容易地获得自己的位置.随着各行各业对基于位置的服务(Location Based Services,LBS)需求不断扩大,对于基于位置的服务研究也不断深入.在我们的日常生活中,道路网上已有很多LBS应用.例如,导航系统、旅游应用程序.
在不同类型的路网中进行k近邻查询需要不同的算法.因此对于每一种路网模型,都会有一些合适的算法来进行k近邻查询.如果路网模型中的边权值是静态的且确定性的,那么这个路网模型就是非时间依赖路网,也称为静态路网.静态路网下k近邻查询的相关研究已十分成熟,文献[1-4]为静态网络提出了许多有效的算法.这些算法均为标准的k近邻查询算法.
而随着城市道路网络上私家车的数量不断增加,越来越多的路网卡口开始发生交通拥堵.这就会导致许多社会问题的产生,例如城市交通污染和居民出行时间的变化.为了能够帮助人们能够更有效地应对外界情况的改变,例如交通状况,天气因素,突发事件就需要时间依赖路网模型.其中,道路边权值跟随时间而产生变化.如图1所示,一位到南京来旅游的游客,他/她对于离他/她最近的旅游景点非常感兴趣,例如最负盛名的几个景点,紫金山、紫峰大厦等.他/她提出一个查询,询问此时此刻哪条路线通往该景点最快;答案取决于出发时间.例如,10:00时,去紫金山需要40分钟(见图1(a)).这是最近的景点.尽管如此,如果他/她在22:00查询相同的问题,在相同的空间点,最近的景点是紫峰大厦(见图1(b)).在静态路网中,无论何时进行k近邻查询,返回的结果都是相同的.而时间依赖路网中的k近邻查询则不同,需要考虑外界因素对路网边权值的影响,更符合实际情况.
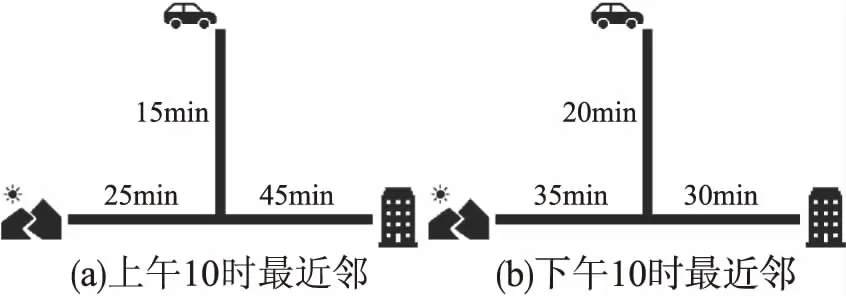
图1 k近邻查询样例Fig.1 Example of kNN query
由于实际路段上的行驶时间由时间决定,也就是说,其取决于路段上当前时间的交通车流量,所以实际路网是时间依赖路网而非静态路网.而在时间依赖路网的k近邻查询,即TD-kNN问题,同时是查询距离查询点最短路径行驶时间的k个POI.但目前TD-kNN的研究大多针对路网静态对象[5],未能有效处理多移动对象服务.例如,乘客查询能最快到达的快车,食客寻求能最快送到的外卖,病人寻求能最快赶到的救护车等.同时查询算法存在许多局限和不足,主要依赖在线扩展,查询时间代价大,仅使用朴素启发函数,近邻扩展还可以进行多次过滤,造成了过多冗余计算,使得算法查询效率受到了一定影响.
基于上述问题,提出新的时间依赖路网上k近邻查询用以解决实际生活中查询k个POI(如快车、救护车、外卖骑手)能在最短时间内到达查询点(如乘客、病人、食客)的问题,并对此构建了一个基于标记点的最短路径树结构,运用三角形不等式和启发式函数,能够有效处理时间依赖路网上移动对象的k近邻查询.本文主要贡献如下:
1)针对以往研究假设时间依赖路网下移动对象查询的不足,提出反向时间依赖路网图上移动对象的k近邻查询,使得最终结果更加接近真实值.
2)提出一种基于标记点的时间依赖路网下最短路径树.并利用三角形不等式和启发式函数,极大地提升了算法的查询效率.
3)采用德国奥登堡路网数据集与现有算法进行了对比实验,进一步验证了算法的有效性,实验结果表明,TDSPT-kNN算法相较于现有算法更为高效.
本文其余部分结构如下:在第2节中,我们对相关工作进行了简要的讨论.接下来我们正式定义了反向时间依赖路网上移动对象的k近邻查询.第4节基于上述概念提出了时间依赖路网下的基于标记点的最短路径树构建及更新,并基于此提出了反向时间依赖路网上移动对象的k近邻查询算法TDSPT-kNN.在第5节,我们给出了实验评估和结果.最后对本文工作进行了总结并对下一步工作提出了思考.
2 相关工作
k近邻查询作为基于位置服务中重要支持性技术之一,已经有众多学者对其深入研究.Knuth提出了著名的邮局问题,NN查询就来源于此.k近邻查询则是NN查询的一般形式化.
传统路网上关于k近邻查询的研究已经相当成熟[6,7].Papadias[6]等提出的INE算法基于传统路网上的Dijkstra算法,从查询位置开始扩展近邻节点,直到找到k个近邻结果.IER[6]算法利用空间剪枝技术(例如,以欧几里德距离为边界剪支)来改进INE算法,剪枝无用扩展.IER和INE都是“盲目”算法,因为它们既不能捕获从对象到查询位置的全局距离,也不能有效地修剪不必要的对象.Lee[7]提出的ROAD算法采用层次结构扩展了Dijkstra算法.算法以递归形式将路网网划分为子网络,预先计算子网络中虚拟边的最短路径距离,并以分层方式组织它们.通过使用类似Dijkstra的网络扩展,道路可以跳过不包含对象的子网络.但是它不能剪除对象广泛分散的子网络.例如,如果对象分布广泛(例如加油站),道路将退化为Dijkstra算法,并且必须穿越整个网络.因此,在大型路网上性能很差.
Cooke和Halsey[8]认为静态路网下的SP问题缺乏现实意义,率先提出节点间通行时间可变的路网.George和Shekhar[9]提出了时间聚合图概念,将每条边上在一时刻的旅行时间聚合成一个时间序列.上述研究均假设边权函数定义在有限离散时间序列t∈t0,t1,…,tn上,但是离散时间算法有许多缺点.首先,由于对于每个指定时间步长中都要复制整个网络,因此对于复杂网络来说,使用离散时间定义的时间依赖路网需要大量的存储空间.其次,使用离散时间定义方法只能提供近似结果,而非精确结果,因为计算是在离散时间进行的,而不是在连续时间进行的.Dreyfus[10]提出了在时间依赖路网下Dijkstra算法的变体,Halpren[11]研究发现时间依赖路网的时间间隔会导致路网的不一致性.Ding[12]等人针对TDSP问题提出了基于Dijkstra的算法,该算法通过扫描时间步长来分离路径选择和时间细化从而优化时间复杂度,时间步长大小取决于到达时间函数值.Kanoulas[13]等人引入了allFP算法,该算法不按标量值对优先级队列进行排序,而是维护所有要扩展的路径的优先级队列.但该算法枚举从源节点到目标节点中的所有路径,所以在最坏的情况下,该算法会产生指数运行时间.Demiryurek[14]等估计通行时间的上下届运用A*算法来扩展路网节点,但这会使得结果是依据估计值,和实际值有一定偏差.
综上所述,目前传统静态路网的近邻查询算法已经有相当多的研究,而时间依赖路网下的近邻查询算法仍存在不足.已有的时间依赖路网下的k近邻查询技术大都是依据出行时间的估计值,和实际时间仍有较大偏差,同时搜索时扩展节点慢效率不高.为解决上述问题,提出反向时间依赖路网上移动对象的k近邻查询问题,并构建了一个基于标记点的最短路径树结构,运用到三角形不等式和启发式函数,提出了一种高效的时间依赖路网下的移动对象k近邻查询算法TDSPT-kNN.
3 基础定义
下面给出对于时间依赖路网模型定义和性质及新的k近邻查询问题.
定义1.(时间依赖有向图[15])将时间依赖路网建模为有向图GT=(V,E,W),其中每个vi∈V是路网中顶点集,evivj∈E是vi到vj的有向边,wvivj∈W是与边evivj相关联的时间依赖路网边权值函数,wvivj(t):[0,T]→R+,T是W中函数的域,表示边evivj在t时刻的通行时间为wvivj(t).
与现有的时间依赖路网算法类似,我们假设时间依赖有向图满足FIFO性质,即用户正好在时间t出发且在通过路径时不允许等待,如果不满足则查询问题将演变成NP-hard问题[16].
定义2.(分段线性权值函数[15])对于给定的一条有向边e,在特定的时间段内与一组权重(行程时间)相关联,如S={(t1,w1),…,(tk,wk)}其中,t1=ts&tk=te,的插值点集记为SI.有向边e的分段线性权值函数记为w,权值函数w是点集SI中的线性插值.在时刻t出发,由vi移动到vj所需要花费的时间,即wvivj(t)在时刻t得出的权值.
本文设定的时间依赖路网图中边不都是双向对等的.即边evivj的存在并不意味着边evjvi的存在.此外,存在相反边evivj和evjvi,使得wvivj(t)≠wvjvi(t),否则研究的问题将变成传统意义上的TD-k近邻问题.如图2所示,这是一个时间依赖局部路网图.对边ev0v1和ev1v0以及ev0v2和ev2v0具有相同的成本.然而,ev0v3和ev3v0虽然相反,但有不同的成本.
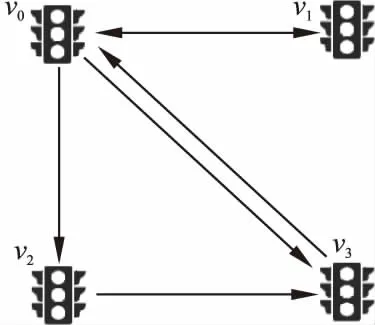
图2 时间依赖局部路网Fig.2 Time-dependent local road network
图2局部路网中的时间依赖边权如表1所示.每个边都与一组(时间,权重)对相关联.

表1 边权值Table 1 Edge weights
定义3.(到达时间[17])对于时间依赖路网图GT=(V,E,W),t时刻从vi点出发,经过边evivj到达vj点的时间记为ATvivj(t)=t+wvjvi(t)modT.
定义4.(路径行驶时间)时间依赖路网图GT=(V,E,W)经过
TT(ρv1vi,t)=TT(ρv1vi-1,t)+wvi-1vi(t+TT(ρv1vi-1,t))
(1)
其中TT(ρv1v1,t)=0.如图2所示,路径p={(v0,v2,v3)} 在t=15 时的路径行驶时间TT(ρv0v3,t)=20+20=40.
定义5.(最短路径时间函数[15])在时刻t从节点vs出发到达ve的最短路径时间函数记为τvsve(t),是所有可能路径集δvsve的最小时间.
τvsve(t)=minρvsve{TT(ρvsve,t)|ρvsve∈δvsve}
(2)
定义6.(兴趣点(POI))设P={p1,…,pn}为兴趣点(POI)pi=(pid,loc,mf),1≤i≤n.其中,pid是POI的标识,loc是p在地理空间(即纬度,经度)中的位置,mf:RxR→V是给定的映射函数,它将p的地理位置与一个顶点v∈V相联.
为了将所提出的反向时间依赖路网上移动对象k近邻查询问题形式化,下面对查询点及查询问题进行定义.
定义7.(查询点)查询点qp∈V是图TDG中的顶点.该查询点qp由用户任意选定.
定义8.(时间依赖路网查询问题)一个查询问题的实例:元组.其中,GT=(V,E,W)即为时间依赖路网图,P是兴趣点集,qp是一个查询点,qp∈V,非负整数qt∈[0,T]指代查询时间,非负整数mtt∈[0,T]指代最大等待时间.给定一个TDRNQ例子,问题是找到满足以下条件的p∈P:
(i)tt(p,qp)≤wt;
(ii)∀π∈V|tt(p,qp)≤tt(pi,qp)&p≠pi
条件1约束行程时间应小于等待时间wt,条件2约束从p到qp的行程时间必须最小,且必须考虑到所有POI.
4 算法描述
本文研究的k近邻查询,致力于解决用户对路网上移动服务的查询需求,是查询能以最短行驶时间到达查询点的k个POI.对此设计了时间依赖路网上基于标记点的最短路径树TD-LSPT,在4.1节给出了相关概述.4.2节依据三角形不等式和启发式函数,进一步提出了TDSPT-kNN算法来解决反向时间依赖路网上移动对象的k近邻查询问题.
4.1 时间依赖路网上的最短路径树及其更新

如图3所示,是边(C,G)权值由21增加到31的情况.粗线箭头就是以A为根节点生成的最短路径树.当边(C,G)权值增加时,节点A、B、C、D、E、G、H、K原最短路径仍是合法的.但对于根节点A到虚线区域内节点的最短路径,必须进行更新.这些节点都是原有SPT中节点F(包含F)的子孙节点.如图4所示,是更新后的新SPT.如果到节点F、I、J、L、M的最短路径不变,则这些节点的最短距离仅增加10.如果存在其他路径可使其距离增值小于10,则进行更新.这些节点都有多条入边.每条入边都可能会定义新最短距离.例如,边(C,F)和(B,F)都可以到达节点F,经过边(C,F)到节点F的路径最短距离将增加10.而通过边(B,F)则最短距离增加2.这意味着边(B,F)更优.如表2所示,列出了虚线区域内节点所需要扫描的边.
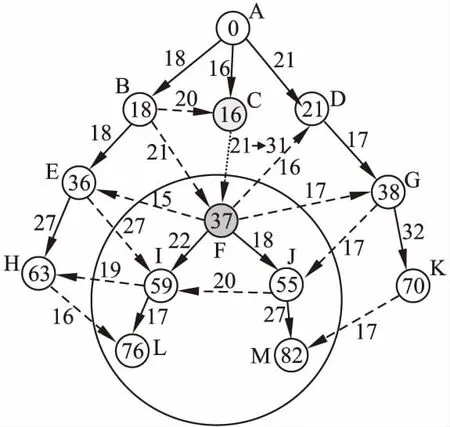
图3 边(C,F)权值由21增加至31Fig.3 Edge(C,F)weight increased from 21 to 31
表2首先列出需要更新的节点,其次列出节点的入边.在第3行中,如果新最短路径包含第2行的入边,则给出距离增值.最后给出入边是否有助于构建新SPT的判断.在给出节点的所有入边中,第2行的边对其节点的增量最小.当从边集Q_SPT中提取一条边时,该边就是一条关键边.在图4中,关键边就是(G,J)和(B,F),即在表2更新的边.

表2 与需要更新的节点相连边会影响新SPT的构建Table 2 Connection edge with the node to be updated will affect the construction of the new SPT

图4 边(C,F)权值由21增加至31所建立的新SPTFig.4 A new SPT based on the weight of edge(C,F)increased from 21 to 31
给定节点集V′,定义源边集S_Edge{N}和终边集T_Edge{N}.其中V′ ⊆V,S_Edge{N}⊆E,T_Edge{N}⊆E.S_Edge{N}={e|S(e)∈N,T(e)∉N};T_Edge{N}={e|T(e)∈N,S(e)∉N}.例如图4所示,节点集V′={F,I,J,L,M},S_Edge{N}={(F,D),(F,E),(F,G),(I,H)},T_Edge{N}={(B,F),(C,F),(E,I),(G,J),(H,L),(K,M)}.即源边集是SPT中与虚线范围相交的且源节点在虚线范围内终节点在虚线范围外的有向边,终边集是SPT中与虚线范围相交的且源节点在虚线范围外终节点在虚线范围内的有向边.
在 TD-LSPT算法中,预处理包括两个步骤:标记点选择和原始SPT生成.标记点的选择是启发式的,所以我们只选择静态标记点,即使后续时间依赖路网变化标记点也不会更改.原始SPT可以通过静态路网中的Dijkstra算法(处理无负权边的图)或Bellman-Ford算法[17](处理无负权环的图)得到.在更新过程中,通过维护边集Q_SPT和节点集合M,重新配置节点的父子关系.集Q_SPT中的每个元素都以{e,min_d}的形式存储,其中min_d表示假设新的最短路径通过e,节点T(e)的最短距离的增加值.M表征当边权增加时受影响的节点的集合,可简化更新SPT的计算.受影响待更新的节点都会被加入到点集M中.设节点v∈M,节点v带有增值M.v.inc.M.v.inc是其入边中最小的增值.同时点集M能确保边集Q_SPT中没有具有相同min_d的记录.当节点S(e1)成为连续变化的临时SPT中节点T(e1)的父节点时,用公式表示为P(T(e1))=S(e1),节点T(e1)则为节点S(e1)的子节点.
更新SPT会根据边权变化进行两种操作.一种处理边权增加,另一种处理边权减小.边权值增加时调用算法1,通过维护集合M能简化添加/删除元素及在边集Q_SPT搜索最小min_d的计算.边权减小时与增加操作类似,但需要注意无法判断更新节点的确切范围,会出现更短的最短距离对des(j)中的所有节点更新的情况.des(j)中节点最短距离的减小也会使其相邻节点更新更短的最短距离.即边权减小的影响可能会传播.当处理完边权变化后会等待下一个拓扑变化.
算法1.UPDATE-Increased算法
输入:原SPT,边e变化前后权值w(e)和w′(e)
输出:更新后的SPT
1.d=w′(e)-w(e);
2.M←j;M.j.inc=d;
3.Q_SPT.Enqueue(e,d) //∀v∈des(j)更新
4.IfT(e)∈des(j)&S(e)∉des(j)then
5.min_d=MIN{D(S(e))+w(e)-D(S(e))}
6.Ifmin_d 7.Q_SPT.Enqueue(e,min_d); 8.m.v.inc=min_d; 9.IfP(k)=vthen 10.M←k;M.k.inc=M.v.inc; 11.ForQ_SPT≠Ødo 12.Q_SPT.Extract(e’,min_d); 13.P(T(e)) =S(e); //原SPT已改变 14. ∀v∈des(E(e′)),D(v)=D(v)+min_d;//更新子节点 15.Ife∈S_Edge{des(T(e′))}&e∈T_Edge{M}then 16.min_d=D(S(e))+w(e)D(T(e)); 17.Ifmin_d 18.M.T(e).inc=min_d;//更新Q_SPT 19.Q_SPT.Enqueue(e,min_d); 20. ReturnQ_SPT 当标记点原有SPT中边权增加时算法1对其进行更新.引入点集M来表示路网图GT中更新的节点.初始化阶段(第1-2行),M包含所有要更新的节点.将节点j和增值d一起加入到节点集M中.然后根据标记点原有SPT中根节点j的DFS序列搜索j的所有子孙节点(第4-5行).v的第一个节点j初始值为M.j.inc.用D(S(e))+w(e)-D(T(e))的增值来比对除去des(j)中具有初始节点后剩余每个节点v∈des(j)的入边.选择增值最小的边e′,将其最小值min_d与M.v.inc进行比较(第6-8行).如果min_d较小,则将边e′添加到边集Q_SPT中,并更新M.v.inc.随后,将临时SPT节点v的子节点k加入到节点集M中,并附上M中节点v的增值(第9-10行).初始化过程确保Q_SPT中每条边的增值都比其所有祖先小.初始化结束后,集合Q_SPT内包含所有关键边. 当边集Q_SPT为空时,策略一的循环终止(第11行).此时已经构建好新SPT,TD-LSPT-UPDATE算法等待下一次边权更改.如果非空,从Q_SPT中提取带有最小增值的边e′(第12行).一旦边e′被取出,其初始节点S(e1)将成为维护SPT中的结束节点T(e′)的父节点(第13行).所有子孙节点des(T(e′))都可以通过增加min_d得到其新的最短距离(第14行).Q_SPT中的所有与des(T(e1))中终节点相连的边都将被移除(第15行).更新的节点也从M中移除(第16行).此外,由于M中的一些节点会得到更小的最短距离增量,会对以des(T(e1))为源节点和M中节点为终节点的边进行筛查(第17-19行).将这些边添加到边集Q_SPT中然后继续执行动态更新. 边权值减小且对原SPT造成影响时也需要对标记点原有SPT进行.因为无法具体到更新哪些节点,所以不再使用节点集M.由于des(j)中所有节点的最短距离都减小了,所以会对des(j)中所有节点进行更新.如果该边对原SPT造成影响则加入Q_SPT.终节点T(e)则选择最小增值min_d的边e′,如果min_d为负,则将边e及其min_d加入到边集Q_SPT中.创建的边集Q_SPT包含所有关键边. k近邻查询算法分为预处理和查询.预处理时建立相关路网和最短路径树;查询时维护标记点的最短路径及利用预处理信息和查询算法返回满足条件的k个对象. 图5 反向时间依赖局部路网Fig.5 Reverse time-dependent local road network 预处理时首先使用路网图GT的初值作为权值,并创建其反向时间依赖路网.再通过4.1节算法选取标记点并生成相应SPT,存储标记点到达其后继节点的最短路径及其最短距离. 当时间依赖路网中有向边的权值发生变化时,根据边权变化执行两种更新操作. 扩展节点进行查询时,越可能成为q最近邻的路网POI优先级越高,而优先级高的会最早扩展.基于三角形不等式和标记节点的动态最短路径树,构造如下启发函数来引导搜索,使每个顶点路径规划始终趋向于最近POI: f(n)=maxl∈L{d(l,t)-d(l,n),d(n,l)-d(t,l)} (3) 式(3)中:f(n)表示从节点n到达终点t的预估距离,对于每个标记节点l∈L,根据三角不等式两边之差小于第三边可知d(n,t)≥d(l,t)-d(l,n)且d(n,t)≥d(n,l)-d(t,l),遍历所有标记节点后将f(n)取值为最大值. TDSPT-kNN算法如算法2所示.依据输入的查询点q的具体路网位置点开始,同时将查询时间点及最大行程时间作为参数,构建优先队列Q_NN来扩展搜索近邻POI,同时用队列R来保存结果集.算法2开始扩展并在1-3行初始化相关值,开始先将查询点q插入到优先级队列Q_NN中(第4行).存放尚未展开扩展节点的队列Q_NN是以四元组(v,TTv,ATv,hv)的形式存储,v是节点,TTv=TT(q,v,t)代表从q到v的行驶时间,ATv=AT(q,v,t)代表到达v的到达时间,hv是启发式函数值加TTv,对于查询点q直接位于标记点,POI位于标记点,查询点q和POI处于同一标记点最短路径树中可直接得出.若是以上3种情况外,则可通过启发式函数hv=TTv+f(v)/vmax引导扩展,f(v)/vmax是从v点到达最近POI的行驶时间的估计.hv小的节点优先从队列Q_NN中出队来进行搜索(第6行),当顶点u出队后,会将其标记为已访问(第7行),如果出队顶点u是POI且hu小于R集合中第k个POI,则将u插入到结果集R中(第10行).由于u是POI,因此hu表示从u到q的通行时间.如果hu已经大于或等于R中第k个POI,则搜索结束,R中前k个POI作为近邻结果集返回(第13行).检查近邻点v的访问标识,为真则跳过(第15行).接着计算当前TT,超过最大行程时间则直接跳过(第16-17行).随着节点的扩展,计算到达时间(第18行). 算法2.TDSPT-kNN算法 输入:查询点q∈V,最大行程时间t∈[0,T] 输出:依据最大行程时间t能以最快时间到达查询点的k个近邻结果集 1.TTmax= 0; 2.ATq=t+dt; //初始化q到达时间 3.kth_R=∞; //结果集R 4.Q_NN.Enqueue(q,TTmax,ATq,hq); //查询点q先进队 5.WhileQ_NN≠ Ødo 6. (u,TTmax,ATu,hq)=Q_NN.Dequeue; //队头u出队 7.u.visited=true; 8.If(TTmax≤t)then 9.If(uis POI)&&(hu 11.If(R.size>k)then 12.kth_R=H′of thek-thobject inR; 1http://www.cs.utah.edu/~lifeifei/SpatialDataset.htm 13.Elsereturntop-k objects inR; 14.Foreachadjacencyvofudo 15.If(v.visited)thencontinue; 16.TTc=u_TravelT+v_dist(u,v);//计算通行时间 17.If(TTc>t)thencontinue; 18.ATc=u_ArrivalT-v_dist(u,v); 19.Q_NN.Enqueue(v,ATc,TTc,Lv);//v进队 为验证TDSPT-kNN算法的性能及其有效性,我们设计了两组实验对TDSPT-kNN算法进行测试.我们提出的TDSPT-kNN算法着力于解决在时间依赖路网中离查询点Q最近的k个兴趣点的问题,所以我们将其与能解决相类似k近邻查询问题的NN-Reverse-TD算法[18]进行比较.NN-Reverse-TD算法利用增量式网络扩展INE算法和启发函数在时间依赖路网上将最近的移动对象及时返回给查询点. 实验环境为:Windows10操作系统,Intel Core i5-3470 CPU @ 3.20GHz 处理器,主频3.20GHz,内存4GB.上述算法均用C++语言实现,编译器为GNU Compiler Collection. 采用Brinkhoff[19]提出的用于路网的移动对象的生成器来创建综合数据集,选取示例中的奥尔登堡(德国)路网图1进行仿真实验.路网图含7035个有向路段和6105个节点,每隔5min对边赋权值.将提出的TDSPT-kNN算法,通过实验对比已有算法NN-Reverse-TD,得出k值与查询响应时间和查询遍历节点个数的关系和兴趣点密度与查询响应时间和查询遍历节点个数的关系.令k为集合 {1,5,10,15,20,25,30},兴趣点密度默认值为0.1.设兴趣点密度为集合{0.05,0.1,0.15,0.2}中的值,k默认值为15.实验参数如表3所示.每个实验都采取控制变量法.为了尽量减少随机性造成的差异,在相同环境下进行30次测试,同时以去掉最大最小值后剩余28次测试值的平均值作为算法性能的参考指标. 表3 实验参数Table 3 Parameters values of experiments 令k∈{1,5,10,15,20,25,30},POI密度取默认值0.1.对不同k值,随机进行30次查询,取除去最大最小值后剩余28次测试值的平均值.如图6所示,两种算法随近邻个数k值从1到30的变化对查询性能的影响.图6(a)比较了TDSPT-kNN算法和NN-Reverse-TD算法在k值增加的情况下的查询响应时间.图6(b)显示随k值增加查询遍历节点个数两者变化的对比.图6(c)显示了TDSPT-kNN算法节点剪枝比例.随着k值从1到30的变化过程中,所有算法的查询响应时间和遍历节点个数与k值正相关,这是因为需要扩展更多的路网信息才能计算出最终结果,而扩展节点的同时会带来响应时间的增加. 图6 近邻个数k值数据量对算法性能的影响Fig.6 Performances with the number of nearest neighbours on algorithm TDSPT-kNN算法遍历节点个数随k值增加而缓慢增加,且性能远远优于NN-Reverse-TD算法.由于TDSPT-kNN算法为基于时间依赖路网中的地标及其相关动态最短路径树,能够有效减少整体扩展节点,优先朝能够以更短时间到达查询点的POI扩展,即查询规划始终趋向于目标终点.而NN-Reverse-TD算法在时间依赖路网下进行近邻搜索扩展时仅将时间依赖路网节点的启发值设为该节点到最近POI之间的距离,因此TDSPT-kNN算法远比NN-Reverse-TD算法遍历节点个数少,算法更高效. 在算法响应时间方面TDSPT-kNN算法比NN-Reverse-TD算法平均减少64.9%.在计算结果时,随着k值的增加,所需要遍历的节点增加,算法所花费的代价就增大.而当k值为1时,算法的开销差距受遍历节点范围影响,相差较小. 将POI的密度设置为0.05,0.1,0.15,0.2,在不同密度下,令k取默认值15随机进行30次查询,取除去最大最小值后剩余28次测试值的平均值.如图7所示,两种算法随路网POI密度的变化,查询响应时间和扩展节点数的变化趋势.本文比较了TDSPT-kNN算法和NN-Reverse-TD算法,得出随路网POI密度变化的查询响应时间的平均值对比曲线.由图7(a)给出了POI密度增加对两种算法的响应时间的影响,TDSPT-kNN算法的查询响应时间一直小于NN-Reverse-TD算法.如图7(b)所示,路网POI密度变化对两种算法遍历节点个数的影响.POI密度增加后,每个点作为兴趣点的概率增加,因此只需要访问更少的顶点就可以返回规定数量的对象结果,两启发式算法耗费的时间也会随之减少.所以如图7(c)所示,TDSPT-kNN算法节点剪枝比例随着POI密度的增加,优化质量有所下降. 图7 POI密度对算法性能的影响Fig.7 Performances with the POI density on algorithm 在路网POI密度对算法性能的影响中,TDSPT-kNN算法比NN-Reverse-TD算法的平均扩展顶点个数减少66.3%,响应时间减少65.7%,这是因为TDSPT-kNN算法采用的启发值更接近实际值,能优先扩展更快到达POI的顶点,因此访问了更少的顶点,降低了算法的响应时间.算法的响应时间和搜索过程中访问到的顶点数目关系密切,因此也可以发现两者的变化趋势大致相同. 本文从时间依赖路网出发,针对路网上移动对象的k近邻查询问题进行深入研究,提出反向时间依赖路网上移动对象的k近邻查询解决方案.在分析现有查询算法的不足基础上,建立了反向时间依赖路网和基于标记点的最短路径树.在此基础上,给出了反向时间依赖路网上移动对象的k近邻查询算法TDSPT-kNN.通过采用基于最短路径树的启发式函数等剪枝策略,进一步提升查询效率.最后,通过仿真实验对TDSPT-kNN算法和已有算法在多种情况下的对比分析,结果表明该方法的高效性.我们未来的研究重点将放在解决弱影响集的相关问题,例如出租车司机更倾向于搭载能收益最大化的乘客.4.2 反向时间依赖路网上移动对象的k近邻查询

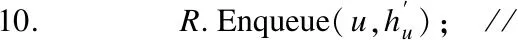
5 实验及分析
5.1 数据集设置

5.2 近邻个数k值变化对算法性能的影响

5.3 路网POI密度对算法性能的影响

6 结束语

