运动控制系统时频特征融合多故障分类
朱俊威,张钧涵
(浙江工业大学 信息工程学院,杭州 310023)
1 引 言
运动控制系统是以电机为控制对象,控制器为核心,执行机构是电力电子和功率变换装置,依据自动控制理论和现代控制理论组成的电气传动控制系统.运动控制系统的应用涉及工农业生产、交通运输、国防、航空航天,甚至在家用电器中都有大量使用[1].运动控制系统使用时存在的磨损、老化等情况可能导致系统故障发生.因不同位置磨损而导致的故障会影响系统的正常工作状态但初期并不会改变系统的稳定性,这就导致了这些故障难以被及时发现.除此之外,机械不同程度的磨损会导致系统性能不同程度的损失,对故障等级的判断能够让系统管理者根据部件磨损程度判断是否需要更换零件.单纯的故障检测虽然不难实现,但若无法辨识系统故障具体的位置、类型以及严重程度,系统管理者需要耗费大量的时间对系统各部件进行故障排查.因此如何对运动控制系统实现多故障分类就显得尤为重要.
过去已有的研究中不乏针对运动控制系统的故障检测与分类[2]:基于模型的方法大都先对目标系统建模并构建状态观测器,由系统实际输出与观测器输出进行比较得到残差,进而实现故障隔离[3].基于模型的方法虽然能够在线实现系统故障隔离,但存在严格的故障隔离条件,而大部分实际系统无法满足,因此该类方法难以对多类故障进行准确辨识.而基于数据驱动的方法虽然无法做到在线隔离,但其并不依赖于系统模型,可以通过提取故障特征处理故障分类问题[4],Huang[5]等将时频压缩与广义解调相结合提取了更高精度的故障特征.部分学者从时域角度提取电机轴承振动信号的特征指标[6]作为机器学习的输入,如裕度指标、脉冲指标、峰值系数[7]等;也有学者从频域角度如用快速傅里叶变换[8]构建原始轴承振动信号的频谱图,并提取固定频率下的振幅作为特征输入支持向量机实现了3类轴承状态下的故障检测,Wang[9]等用短时傅里叶变换等方法提取时频图像作为卷积神经网络的输入,Jordi[10]等利用改进的短时傅里叶变换使其只对轴承振动信号的特定频段进行滤波,大大减少了故障分析所需的时间.相比短时傅里叶变换,小波变换设计了尺度可变换的时频窗口,Rahman[11]等将小波变换与其他方法比较得出,在对机械的早期故障检测中小波变换能够更准确的识别故障的位置以及严重程度.Elbouchikhi[12]等使用经验模态分解获取电流信号的本征模函数(Intrinsic Mode Function,IMF),根据IMF的瞬时幅值、瞬时频率、能量以评估故障的严重程度.葛兴来[13]等提出了将经验模态分解与奇异值分解结合的多层分解方法,从而更好地剔除干扰并提取故障特征.
现有关于运动控制系统多故障分类的研究成果较少,当考虑到多故障模式下运动控制系统的故障定位问题时,以上单一的特征提取方法存在一定局限性,例如:若仅提取时域指标[6,7],则无法识别卡死故障等状况下系统输出信号内的零频特征,分类效果不佳;若仅使用快速傅里叶变换[8]或经验模态分解[12]提取频域特征,则无法判断执行器等位置部分失效故障的程度.因此本文设计了时频结合的新型特征提取模块,使时频特征融合互补,基于系统输出信号实现了运动控制系统多故障分类,经实验证明具有更高的准确率.
基于上述分析,本文研究了运动控制系统的多故障分类问题.本文主要有以下贡献点:1)建立了运动控制系统的常见故障模型,并分析了不同故障模态对系统的影响,在此基础上设计了一组具有较高故障模态区分度的时频域指标;2)针对带有一般多故障模态的运动控制系统,首次提出了可操作的数据驱动多故障分类模型.
2 问题描述
2.1 运动控制系统组成及其原理
本文所使用的运动控制系统[14]如图1所示,主要由PC上位机,ARM单片机,CAN总线以及交流伺服电机系统组成.PC上位机主要负责处理ARM单片机上发的数据信息,使用算法进行相应的处理后将指令下发给ARM单片机.ARM单片机一面接收交流伺服系统经CAN总线传输而来的电机位置、转速、力矩等信息并将其封装后上传到PC机,一面将PC机发送的控制指令传输给交流伺服系统,使其跟随指令做出相应运动.交流伺服驱动器是台达公司ASDA-A2系列伺服驱动器,额定功率400W,额定电压220V;电机是台达公司三相永磁同步电机,额定电压220V,转速最高达1500rpm,电机框架尺寸60mm.
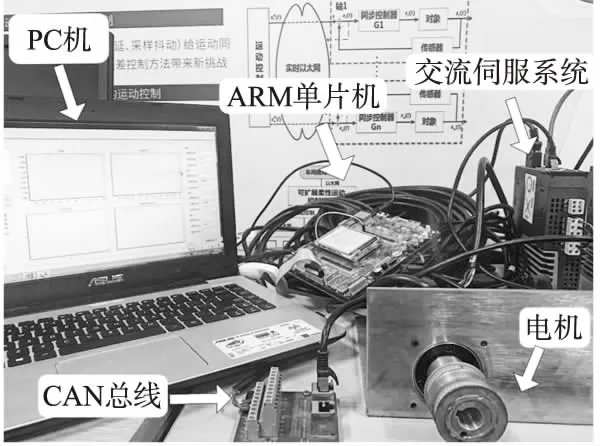
图1 运动控制系统Fig.1 Motion control system


(1)
在上位机中设计一个虚拟参考系统,使伺服系统下真实的电机跟踪其运动状态.参考系统动态模型如式(2)所示:
(2)
电机模型如式(3)所示:
(3)
设跟踪误差δi=xi-x0,则跟踪误差系统模型为:
(4)
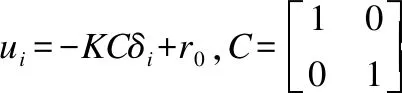
2.2 故障类型及问题描述
表1描述了本文考虑的运动控制系统常见的故障模态以及相应在系统模型中的表现形式.

表1 故障问题描述Table 1 Fault description
尽管电机模型已知,本文主要针对电机历史数据展开多故障分类研究.需要指出,在模型已知条件下出现了不少故障检测和隔离的相关结果[3,16],然而,在线故障辨识方案主要针对单独的传感器、执行器或过程故障进行检测和隔离,因而无法对一般多故障分类问题作有效处理.针对电机历史数据展开多故障分类研究尽管存在检测上的小幅延迟,但大幅缩短了实际工程中故障精确隔离所需时间.另一方面,由于故障早期主要对系统稳态性能产生影响,并不会直接破坏系统的稳定性.因此,针对电机历史数据展开多故障分类分析对于故障早期的有效检测和隔离仍具有重要的实际意义和可行性.
3 多故障分类模型
本文设计的多故障分类模型主要包含三个模块:故障检测模块,时频特征提取模块,基于支持向量机的多故障分类模块.下文将阐述每个模块的工作机理.
3.1 故障检测模块
采用异常检测法[17](Anomaly Detection)对系统历史数据进行故障检测.首先采集历史数据y,取大小为M的移动窗口在y上移动,得到Z个移动窗口样本:
φi=[yi,…,yi+M]i=1,…,Z
(5)
P(i)越小则表明该时刻出现异常的概率Pa(i)=1-P(i)越大(此处概率表示该点状态的异常程度,并非故障的可能性).以正常状态下概率的峰值ε作为阈值,当检测到某个采样点异常的概率高于阈值时,系统发出警报.
(6)
以4类状态的输出位置信号为例,如图2所示,不同故障间、不同故障与正常状态之间波形的区别较小.在工业生产中,若仅凭肉眼进行故障检测,难以确定波形变化是由于故障还是扰动,费时费力且容易误判.而本文设计的故障检测模块只需获得系统输出的历史数据即能对12类故障下的运动控制系统实现高效且准确地检测.

图2 4类系统状态下的位置输出Fig.2 Position output under four types of system states
3.2 时频特征提取模块
当故障发生时,运动控制系统输出位置、转速信号的频率与幅值发生相应变化,各频段间的能量复杂度也随之改变.因此从时域和频域两个角度提取系统输出位置、转速信号的特征.下文将给出时频特征模块具体指标设计过程.
3.2.1 频域特征
聚类经验模态分解(ensemble empirical mode decomposition,EEMD)是在经验模态分解(EMD)的基础上,先在目标位置、转速信号上加入适当大小的高斯白噪声序列如式(7)所示,其中ni(t)是第i次添加的白噪声序列,hi(t)是第i次添加白噪声后的信号,k为添加白噪声的次数.
hi(t)=y(t)+ni(t) 1≤i≤k
(7)
再将hi(t)按照传统的EMD方法分解为本征模函数IMFi,求得k个IMF的均值从而消除白噪声影响,见式(8),得到原始信号经EEMD分解后的IMF矩阵Q.
(8)
EEMD相比EMD能够更好的区分不同频段的信号,并且能够抑制模态混叠现象,保存数据的动态特性,很适合处理多故障分类问题.IMF能量熵表示信号内部各频段间信息的混乱程度.当系统出现卡死或中断故障时,标称的EEMD方法通常提取IMF标准差或奇异值等特征指标[18],但在本文考虑的多故障问题下,该类指标对不同故障的区分度不够明显.本文针对性地考虑到信号内频段数的增加必然导致信息混乱程度加剧进而使得能量熵增大,仅需提取能量熵特征即可达到较好的分类效果.因此根据式(9)提取IMF能量熵S作为频域特征,其中E(i)表示第i阶IMF的能量,K表示IMF的总阶数.
(9)
然而,执行器卡死故障与中断故障均会导致转速信号中出现零频部分,仅凭能量熵特征无法将两者区分.因此引入下文中的时域特征对故障做更精确的分类.
3.2.2 时域特征
本文选择裕度指标z,峰值max,峭度q,标准差c,能量e作为时域特征.其计算公式见式(10),其中y为待处理的电机位置、转速信号,yi为y上第i个采样点,N为信号长度,p为每组信号的方根幅值,μ为信号的算术平均值.
(10)
在其他考虑较少故障情形的研究中,仅凭标准差指标能达到不错的检测与分类效果.然而本文共考虑了12类故障模态下的分类问题,单一特征指标下不同类型的故障特征值很可能发生混淆.因此需根据不同故障模态下系统输出响应的特点设计出具有较高故障模态区分度的时域指标,使得故障能由不同的特征指标区分.例如位置传感器部分失效或过程故障发生时,两者均导致输出信号标准差减小.此时仅凭标准差特征无法区分两类故障,但可使用峰值、裕度指标等将其区分,具体原理可见下文分类依据.
3.3 基于支持向量机的故障分类模块
3.3.1 故障分类依据

当执行器存在部分失效故障时,随着失效等级的提升,执行器无法达到控制器给定的参考值,输出信号幅值减小,波形趋于平缓,峭度减小,离散程度减小,标准差减小,能量指标减小.综上所述可根据时域特征的变化判断执行器、传感器的部分失效等级.
当执行器发生卡死故障时,与部分失效故障不同的是转速信号中出现零频部分,因此引入基于能量熵的EEMD分解提取频域特征进行分类.同理,当位置/速度传感器卡死故障时,用EEMD分解位置/转速信号提取其中的IMF能量熵进行分类.当执行器出现中断故障时,系统控制量突变为0,系统停机,电机转速为0,电机位置固定在某个常值,信号的时频域特征均发生显著变化,多故障分类模块能将其与其他故障很好地区分.
结合上文的时频域特征分类依据,图3详细地描述了本文如何用不同的时频域特征区分不同位置、类型的故障.

图3 故障特征分类依据Fig.3 Faults classification according to feature
3.3.2 多故障分类支持向量机
支持向量机(support vector machine,SVM)是一种基于统计学习理论的学习方法,根本目的是为了寻找一个能将正负样本区分开的超平面.
假设有N个样本{si,li},i=1,2,…,N,li是si样本对应的标签,li∈{l1,l2,…,lk},k为类别数.支持向量机旨在通过式(11)来设计出式(12)形式的超平面分类器.其中ω=(ω1;ω2;…;ωN)是法向量,决定了超平面的方向;b是位移项,关系到原点和超平面之间的距离,因此是由ω和b两个参数决定超平面的位置.
(11)
f(x)=sign(ω·s+b)
(12)
为解决本文考虑的运动控制系统多故障分类问题,根据表2中的训练集分布构建多故障分类模块.以训练样本位置、转速信号的时频域特征作为SVM的输入信号,在任意两类故障间训练一次SVM模型.本文考虑了12类故障,则多故障分类模块中共包含12*(12-1)/2个SVM模型.本文考虑的故障类型基本囊括了常见的运动控制系统故障,实验中模型训练用时0.107s,且实际应用中SVM模型是提前训练完成的,因此即便需考虑更多类型的故障也能满足实际需求.当系统需对某样本进行分类时,提取样本时频特征后将其导入以上SVM模型中,根据66个SVM模型的投票结果输出该样本的故障标签li.
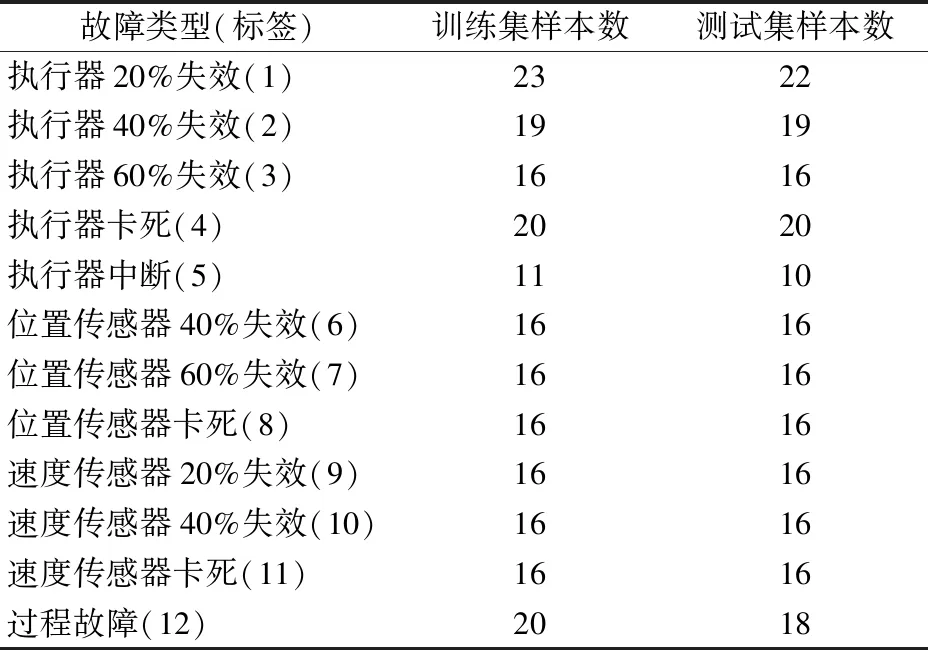
表2 实验样本集分布Table 2 Distribution of experimental sample set
本文设计的多故障分类模型首先根据电机无故障模式下的运行数据构建故障检测模块,继而根据故障时系统的不同输出响应特征设计时频域特征提取模块,最后基于支持向量机构造多故障分类模块.由上述3个模块组成的多故障分类模型旨在对系统状态进行有效监测,并在此基础上进行准确的故障分类.
4 实验验证

图4 执行器故障下的输入uFig.4 Input u of actuator faults
图5为运动控制系统多故障分类模型应用流程图.实际应用中,系统产生的电机数据经故障检测模块判断是否存在异常.一旦检测到异常数据,时频特征提取模块提取异常信号的特征,将其结合后导入基于支持向量机的多故障分类模块中,经分析计算后得出该样本的故障类别.

图5 基于时频特征提取的多故障分类测试流程图Fig.5 Multi-fault classification test flow chart based on time-frequency feature extraction
故障检测.为了检验故障检测模块的有效性,对正常状态下的系统依次加入不同类型的故障.按照上文中介绍的异常检测法分别分析位置/转速信号得到了图6的故障概率图.用表2中的故障标签在图中标注出不同故障的发生,将正常状态下的概率峰值(图中虚线)作为阈值,当不同故障发生时,故障样本位置或转速信号的相应故障概率Pa(t)超出阈值线.例如速度传感器故障(故障9,10,11)虽然无法在位置信号中被检测到,但在对转速信号的检测中能被及时发现.图6表明该方法能够及时有效地检测到本文考虑的所有故障.

图6 故障检测效果图Fig.6 Result chart of fault detection
特征提取.测试集系统数据经采集后先通过故障检测模块判断有无异常,再将其划分得到表2中的测试集样本分布.将测试样本导入时频特征提取模块中,提取每个样本位置与转速信号的裕度指标、峰值、峭度、标准差、能量指标,共10个时域特征.再用EEMD分解位置、转速信号,每组信号重复添加10次均值为0,标准差为0.01的白噪声,得到每个样本的IMF,取其IMF能量熵Sx,Sv作为频域特征.
图7为执行器卡死故障下的转速信号经傅里叶变换后得到的频谱图,可发现信号中的零频部分被有效地分离出来.因此使用EEMD方法分解信号,提取IMF能量熵特征来区分卡死/中断/速度传感器卡死故障与其他类型故障.

图7 执行器卡死故障下转速信号频谱图Fig.7 Spectrum of speed signal under actuator stuck fault
图8为测试集中各类故障在不同特征指标下的特征值分布,以图中3个指标为例展示时频融合模块下不同故障的区分度,用不同标记符表示相应的故障状态,其序号对应表2的故障标签,并用虚线分割相邻的不同故障.结合上文的故障分类依据,时域指标能够区分大部分故障,但对执行器卡死等少数故障类型识别效果不佳,如图8(a)所示,执行器卡死,传感器卡死的特征值均与其他类型故障存在混淆,而此时能量熵指标能从卡死故障中提取零频信息作为分类依据,从频域角度对故障做出区分;反之亦然,如图8(c)所示,执行器卡死、中断和速度传感器卡死故障相比其他故障下特征值更大,频域指标能较好区分上述几类故障,但对部分失效等类型故障的区分度不大,此时可通过时域指标提取信号幅值等信息将其区分.综上可知,本文根据不同故障模态对系统的影响而设计的12个时频域特征能有效区分不同类型的故障.
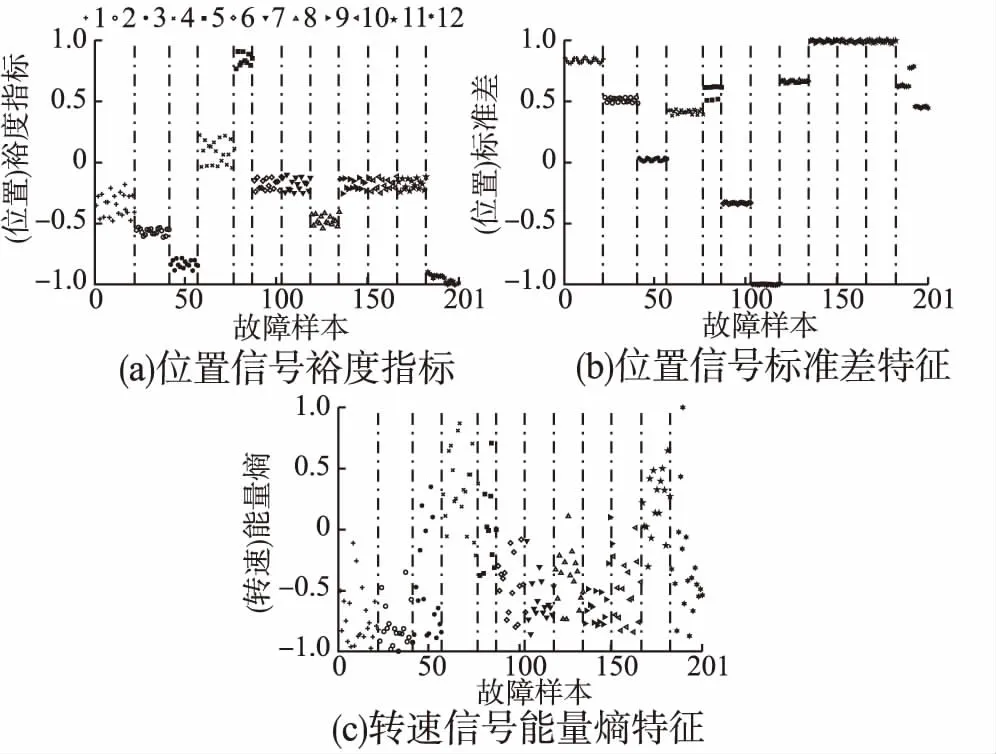
图8 不同故障在某特征指标上的分布Fig.8 Distribution of different faults on a certain feature
多故障分类.提取测试集12个时频域特征后将其作为输入导入上文中训练好的多故障分类模块中,将SVM输出的故障标签与实际故障类别进行比较(实验中SVM对测试集分类用时0.02s),分析得出本文多故障分类模型的准确率.
根据文献中基于时域或频域的特征提取方法与本文的时频特征提取模块进行对比,效果如图9所示.经EMD分解[12]获取的IMF频域指标无法识别不同失效等级的执行器、传感器故障,基于无量纲时域指标[7]的特征提取方法虽然能够识别大部分故障类型,但无法区分执行器卡死等存在零频特征的故障,因此本文通过时频融合实现了特征间的优势互补,准确率大幅提升至98.50%.

图9 多故障分类准确率Fig.9 Accuracy of multi-fault classification
5 结 论
本文针对多故障模式下运动控制系统,分析不同故障模态对系统的影响,设计了一组具有较高故障区分度的时频域指标,在此基础上,利用历史数据训练生成了符合实际工程需求的可操作的数据驱动多故障分类模型.实验测试结果说明本文所提模型具有较高的故障分类准确率.同时,与单一的时域或频域指标方法相比,该模型的故障分类性能更优.

