基于多层感知器神经网络的路径损耗预测研究

吴丽娜 何丹萍 艾渤 王剑 官科 钟章队

（1.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；2.北京高速铁路宽带移动通信工程研究中心，北京 100044；3.北京轨道交通电磁兼容与GNSS技术工程研究中心，北京 100044）

引 言

信道是电磁波从发射机天线传播至接收机天线的媒介. 无线信道建模是探索和表征电磁波在媒介中传播规律的过程，可为无线通信系统的设计、评估和部署等提供强有力的理论指导. 随着无线通信系统的快速发展，尤其是5G无线移动通信系统提出以来，信道数据呈现海量、高速、多样等特性，致使5G及未来通信系统的网络规划与优化面临严峻挑战. 因此，急需建立准确、高效的无线信道模型.

传统的信道建模方法主要包括：统计性信道建模[1-3]、确定性信道建模[4]和半确定性信道建模[5].统计性信道建模基于大量测量数据获取信道参数的统计性特性，建立信道模型；但由于未考虑测量场景的详细信息，该方法较难描述电磁波在场景中的传播过程，不能准确刻画无线信道特性. 确定性信道建模利用传播环境的几何结构和结构体表面材质的电磁特性，依据几何光学理论和电磁传播理论建立无线信道模型. 射线跟踪(ray-tracing，RT)法[6]是基于电子地图的确定性信道建模和仿真方法，该方法利用准确的三维环境模型、天线模型以及电磁波传播模型可准确表征无线信道特性. 相较于统计性信道建模方法，RT法无需进行大量实际测量，但其准确性高度依赖于三维环境模型的精度. 在大规模复杂场景中，三维环境建模的复杂性和材质的多样性都严重影响RT法的计算效率和准确性. 半确定性信道建模方法综合了统计性信道建模和确定性信道建模的优点，降低了计算复杂性的同时又较准确地预测出电波传播特性. 该方法主要包括随机几何建模和相关矩阵法：随机几何建模是对RT法的一种简化方法，不需要电磁波传播环境的详细信息；相关矩阵法利用测量数据的统计特性得到路径时延、入射角和出射角等信道参数，建立信道模型. 相较于确定性信道建模而言，该方法虽然复杂度低，但准确性较差.因此，如何兼顾无线信道模型的准确性和高效性是值得探究的一个重要问题.

无线信道是一个时变的非线性系统，涵盖时域、空域和频域等多维信息. 传统信道建模方法难以应对海量、高速和多样的无线信道发展趋势. 机器学习具有强大的学习和预测能力，可在复杂环境中自动学习数据间的结构关系，以解决非线性系统问题. 同时，机器学习擅于提取高维数据的特征信息，可以显著提高数据处理速率[7]. 因此，机器学习被视为分析无线电波传播过程和建立信道模型的有力工具[8]. 此外，随着大数据、云计算和人工智能的快速发展，智能通信是5G乃至未来无线通信系统的主流趋势之一.

人工神经网络(artificial neural network, ANN)是机器学习中的一个重要分支，具有自适应性、自学习性和高鲁棒性等优点，可用于解决非线性系统问题.路径损耗是无线信道建模中的重要参数，用于表征电波传播过程中功率密度的降低，反映了电波传播特性和信道特性. 目前，基于ANN的路径损耗预测已取得一定成果. 文献[9]构建了径向基函数神经网络(radial basis function neural network，RBFNN)，并将收发天线的高度、距离与载频作为网络输入，实现了路径损耗的准确预测. 文献[10]分别为视距(line-ofsight, LoS)和非视距(non-line-of-sight, NLoS)建立了不同的路径损耗模型，相较于LoS条件下的神经网络模型，NLoS下的预测模型还融入了利用传统模型计算的绕射损耗，对比分析验证了神经网络和传统模型相结合的混合路径损耗模型准确性更好. 文献[11]分别基于分层递归神经网络(layered recursive neural network，LRNN)、聚焦时延神经网络(focusing on the time delay neural network, FTDNN)和分布式时延 神 经 网 络(distributed time-delay neural network，DTDNN)构建了三个路径损耗模型，并对比分析了三者的预测性能，结果表明基于LRNN和FTDNN的路径损耗模型优于基于DTDNN的路径损耗模型. 文献[12]提出了一个结合ANN、高斯过程和主成分分析的机器学习框架；与传统的路径损耗模型相比，该框架具有更高的精度和灵活性，有利于无线通信系统的设计与部署. Sotirios等人[13-15]提出了一种基于ANN的路径损耗预测方法，将差分进化算法与误差反向传播算法(back propagation, BP)[16-17]相结合，显著提高了系统的整体性能. Popoola等人[18-20]基于ANN和自适应神经模糊推理系统建立了甚高频(very high frequency, VHF)和 超 高 频(ultra high frequency,UHF)频段的路径损耗预测模型，并与随机信道模型进行了对比分析；结果表明基于ANN的路径损耗模型比随机信道模型具有更好的预测精度和泛化能力.文献[21]基于卷积神经网络和三维地图的RGB信息建立了毫米波路径损耗模型，结果表明该模型能够准确预测路径损耗，且对环境变化不敏感.

在现有的基于ANN的路径损耗预测中，往往将表征信道特性的信号参数作为ANN的输入，鲜有研究考虑传播环境对信道建模的影响. 无线信道所处环境非常复杂多变，且环境中物体的结构和表面材质的电磁特性是影响电波传播的关键因素，将环境信息融入网络训练中，可提升无线信道建模的准确率. 在缺乏精确的传播环境信息条件下，本文基于有限的地物类型，提出了一种表征电波传播环境的简易方法. 结合测量数据和表征场景信息的环境特征，基于多层感知器(multi-layer perceptron, MLP)神经网络建立了路径损耗模型. 将建立的路径损耗模型与典型的路径损耗模型对比分析，结果表明，在无需繁琐的三维场景建模条件下，基于MLP神经网络的路径损耗模型准确性更高.

1 传播环境的简易表征方法

障碍物是无线电波传播物理环境中最重要的组成部分. 对于大规模复杂环境而言，三维环境建模的复杂性和环境中物体表面材质的多样性都严重影响信道建模的准确性和效率. 利用传播环境中有限的地物类型来表征传播环境，可避免三维环境建模，提升信道建模的效率.

1.1 电波传播数据的采集与处理

电波传播数据关乎信道建模结果的准确性，本文利用连续波(continuous wave, CW)测量方法在中国杭州地区采集无线电波传播数据. 首先，在杭州地区选择三个不同位置部署基站，该地区的栅格化电子地图和卫星地图以及三个基站(BS1, BS2, BS3)的位置如图1(a)和(b)所示，其中卫星地图源为高德地图. 其次，搭建包含发射系统和接收系统的测量平台.发射系统中，三个基站的信号源均产生频率为2.5 GHz的连续波，发射天线为各向增益为0 dBi的全向天线，天线高度依次为62 m、30 m和41.7 m，发射功率均为42 dBm. 接收系统中，接收机部署于测量车辆的顶部，接收天线为各向增益为0 dBi的全向天线，高度约为2 m. 测量平台的详细配置如表1所示.然后，测量车辆分别围绕三个基站沿特定线路采集所有路测点处的接收功率，测量轨迹如图1 (c)所示.同时，接收端外接全球定位系统(Global Positioning System, GPS)同步记录所有路测点的位置信息. 最终，围绕BS1、BS2和BS3分别采集了10 184个、9 988个和3 720个不同位置处的接收功率值. 结合测量配置，每组测量数据对应的路径损耗由下式可得：

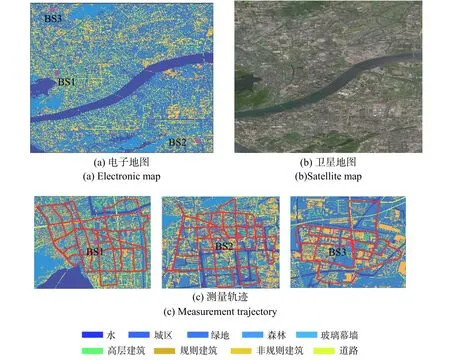
图1 测量场景与轨迹Fig. 1 Measurement scenario and trajectory

式中：L表示路径损耗的测量值；PTx表示发射功率；LBS表示基站的馈线损耗；PRx表示测量采集的接收功率值.

1.2 环境特征的定义与提取

真实物理环境中结构体表面材质的电磁特性是影响电波传播的重要因素，而不同地物类型表面材质的电磁特性不同，相较于精准的三维电磁环境信息，不同地物类型的分布可一定程度上表征电波传播环境.

如图1(c)所示，为统计杭州地区的地物类型分布情况，对其电子地图进行了栅格化处理，栅格尺寸为5 m×5 m，且每个栅格仅代表一种地物类型，地物类型e在测量场景中的百分比可表示为

式中：ne为 测量场景中地物类型e的 数目；Nclutter为测量场景中所有地物类型的数目.

统计可知，图1 (c)中三个基站对应的测量场景内共包含9种地物类型，不同地物类型的栅格数及不同地物类型在整个测量场景中的百分占比如表2所 示.

表2 地物类型栅格数及其百分比Tab. 2 Clutter type and percentage

基于测量可知任意接收机与关联基站的三维空间位置信息，则基站和接收机在二维栅格化电子地图上的投影点可确定一条直线L. 根据直线L穿过的每个地物类型的线段长度，可定义该组测量数据的环境特征Fclutter：

式中：Fi表示直线L穿过第i个地物类型的线段长度；N=9表示测量场景中地物类型的数量.

2 路径损耗模型

2.1 模型评价指标

本文以误差均值(mean error, ME)、误差标准差(standard deviation, STD)和预测结果与测量结果之间的相关系数 C orr作为评价路径损耗模型性能的指标.三者的表达式如下：

式中：l为路径损耗预测值；Nsample为预测样本数； μL、μl和 μerror分别为路径损耗测量结果均值、预测结果均值以及测量与预测结果间的误差均值.

ME和STD是衡量预测精度的常用度量. Corr用于评估预测结果和测量结果之间的线性相关性.若预测结果越接近测量结果，则两者之间的相关性越大，相关系数越接近于1. 反之，若预测结果和测量结果之间存在较大差异，则两者之间的相关性较低，相 关系数趋于0.

2.2 经典路径损耗模型

经典的路径损耗模型可分为两类：基于电波传播物理原理的模型和基于数据拟合的数学模型. 结合上述实际测量数据，考虑两种常用的路径损耗模型，即自由空间临近(close-in, CI)参考距离的路径损耗模型[22-24]和AB(α-β)路径损耗模型[25-26].

CI模型基于无线电波传播原理和Friis自由空间传播模型，路径损耗表达式为

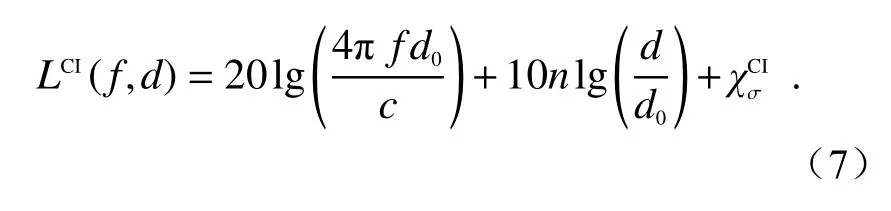
式中：f表示频率；d0表示自由空间的相对参考距离；c表示光速；n表示路径损耗指数，自由空间中n=2；d为基站与接收机之间的三维距离；是阴影衰落，是标准差为 σ 的零均值高斯随机变量. 因实际物理环境中，1 m以内通常不存在明显障碍物，路径损耗模型只需要考虑损耗指数. 同时，已有研究表明使用不同相对参考距离时，CI模型误差没有显著差异[27-28].故本文选择的相对参考距离为1 m.

AB模型是基于测量数据的最佳拟合，路径损耗表达式为

式中：α和β分别表示拟合曲线的斜率和截距，自由空间中 α=20；为阴影衰落，是标准差为 σ的零均值高斯随机变量.

图2给出了不同基站的路径损耗测量结果和预测结果. 表3总结了CI模型和AB模型的参数和评价指标. 由表3可知，AB模型中的斜率 α ＞20，CI模型中的路径损耗指数n＞2，表明测量场景中存在大量NLoS径. 由于BS2较低的天线高度和其测量区域内大量的高层建筑使电波在该区域内传播时产生更多NLOS径，进而导致BS2的路径损耗指数大于BS1和BS3的路径损耗指数. 虽然AB模型和CI模型对应的ME都小于1 dB，但STD均大于7 dB，且Corr均小于0.8. 由此推断，CI模型和AB模型只能尽可能地拟合所有路径损耗样本的总体趋势，但不能准确预测同一距离范围内具有较大偏差的路径损耗值. 且不同测量场景需要不同的CI模型和AB模型，难以应对海量、高速和多样的无线信道发展趋势. 因此，建立兼顾准确性和高效性的路径损耗模型是无线信道建模中的一个重要问题.

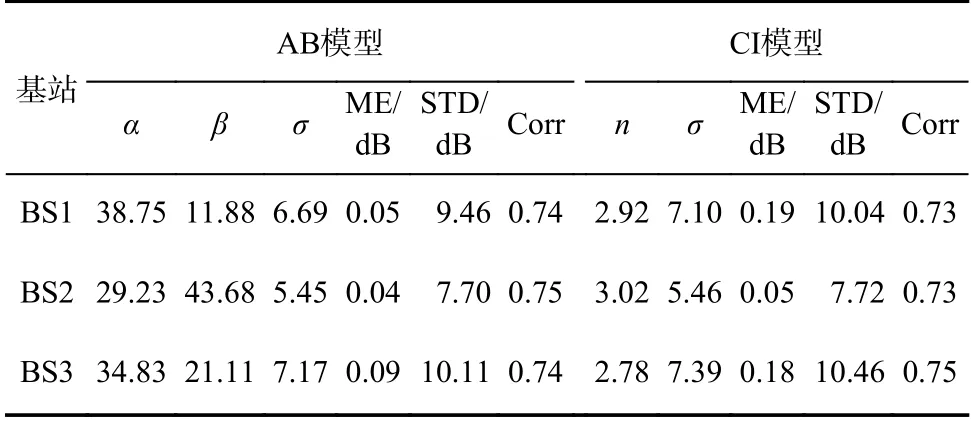
表3 CI模型和AB模型的参数和评价指标Tab. 3 Parameters and evaluation indicators of the AB model and the CI model

图2 三个基站的路径损耗测量结果和预测结果Fig. 2 Measurements and predictions of path loss in 3 BSs

3 基于MLP的路径损耗预测

MLP神经网络包含输入层、输出层和多个隐藏层，是一种基于BP算法训练的多层前馈神经网络.在众多神经网络架构中，MLP神经网络结构简单、易于实现，且具有良好的容错性、鲁棒性以及极强的非线性映射能力[29]. 本节基于MLP神经网络建立路径损耗模型，并和上述经典路径损耗模型进行对比分析.

3.1 网络数据集的构建

ANN是数据驱动型的数学模型，网络数据集直接影响路径损耗的预测结果. 为探究环境特征的有效性和提出的路径损耗模型的性能，由测量信息和环境特征的不同组合构建两种网络数据集：无环境特征数据集和携带环境特征数据集. 前者仅将基站和接收机的相对位置作为训练神经网络的输入集；后者不仅考虑基站和接收机的相对位置，还将提取的环境特征融入到神经网络的输入集中. 神经网络的期望输出，即目标集由公式(1)计算得到的路径损耗测量数据组成.

3.2 路径损耗模型的建立

对于ANN，隐藏层层数和神经元数目的选择恰当与否直接影响模型的性能. 若隐藏层层数和神经元数目过少，网络不具备必要的学习能力和信息处理能力；反之，若网络结构过于复杂，网络学习速率低，易于出现过拟合问题，影响网络的泛化性.

如何选取隐藏层层数与神经元数目，目前还没有明确的理论与方法. 一般情况下，MLP神经网络中隐藏层神经元数目可由如下两个经验公式确定：

式中：NH为 隐藏层神经元数；NI为输入层神经元数；NO为 输出层神经元数；α是取值为1～10的任意整数；Ntraining为训练样本数.

基于式(10)和网络数据集中输入数据的维数，最终选取隐藏层层数为2、神经元数目为63的网络架构建立路径损耗模型. 其他参数的设置如下：学习率为0.1；优化器为自适应矩估计(adaptive moment estimation, Adam)[30]；训练样本从三个数据集中随机选取，且训练样本量占总样本量的70%，其余30%的样本作为模型的测试样本；训练次数为10 000.

图3为无环境特征数据集和携带环境特征数据集下基于MLP神经网络的路径损耗模型对测试样本的预测结果. 无环境特征数据集中测试样本的ME、STD和Corr分别为0.38 dB、5.20 dB和0.9；携带环境特征数据集中测试样本的ME、STD和Corr分别为0.07 dB、4.33 dB和0.94. 由此可知，无论是否携带表征电波传播场景的环境特征，MLP神经网络均可实现路径损耗的高精度预测. 相较于无环境特征数据集，携带环境特征的数据集有助于MLP神经网络自动学习传播场景的环境信息，建立电波传播多径与环境中结构体的映射关系，提升模型的准确性. 此外，该方法未为不同基站建立不同的路径损耗模型，而是将所有基站的关联数据同时作为MLP神经网络的输入，建立统一的路径损耗模型，且预测结果仍然优于AB模型和CI模型的预测结果.

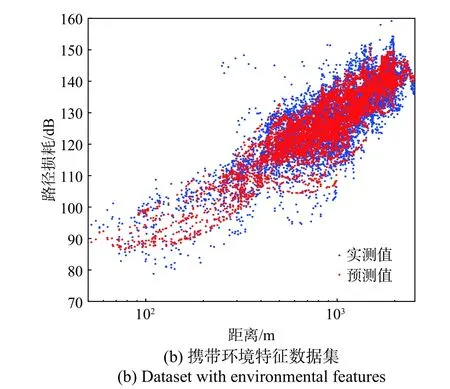
图3 不同数据集中测试样本的预测结果Fig. 3 Prediction results of testing samples in different datasets

4 模型泛化性分析与改进

4.1 路径损耗模型的泛化性分析

泛化性是指模型对新数据的适应能力，是评估模型性能的一个重要指标. 本节根据基站不同将测量数据进行分组，利用部分基站数据作为网络训练集，其他基站数据作为测试集，以测试模型的泛化能力. 利用BS2和BS3的测量数据构建网络训练集，BS1的测量数据构建测试集.

图4为基于MLP神经网络的路径损耗模型对BS1区域内测量点处路径损耗的预测结果，其ME、STD和Corr分别为0.07 dB、8.10 dB和0.74. 神经网络是数据驱动型的数学模型，通过学习训练样本的数据特征实现对测试样本的预测. 由表2可知，三个基站所处场景存在较大差异，BS1区域内采集的测量数据的特征信息不完全和BS2区域内以及基站3区域内采集的测量数据的特征信息相吻合，所以分基站预测下模型的性能稍有降低. 此外，结合BS2和BS3的测量数据建立了AB模型，并用此模型预测BS1区域内路测点处的路径损耗，预测结果的ME、STD和Corr分别为1.68 dB、9.57 dB和0.59 dB. 类似地，在相同测量数据分配方式下建立了CI模型，且该模型对BS1区域内路测点处路径损耗预测结果的ME、STD和Corr分别为1.44 dB、10.01 dB和0.65 dB.由此可知，基于MLP神经网络的路径损耗模型虽易受电波传播环境的影响，但其预测性能仍然优于经典的AB模型和CI模型.

图4 基于MLP神经网络的路径损耗模型对BS1区域内测量点处路径损耗的预测结果Fig. 4 Path loss prediction results of the measurement points in BS1 under the MLP neural network-based path loss model

4.2 路径损耗模型的改进

由于未充分考虑场景的三维空间信息，提取的环境特征有助于MLP神经网络学习场景信息的同时，可能引入不参与电波传播的地物干扰，影响路径损耗模型的准确性. 同时，由携带环境特征的数据集训练生成的路径损耗模型不适用于存在较大差异的其他场景，即环境特征的引入影响提出的路径损耗模型的泛化性. 针对上述问题，本节利用测量数据的LoS和NLoS标签，改进环境特征的定义，尽可能删除干扰地物，提升模型的性能. 若测量数据是LoS径，则基站和接收机之间的地物类型不影响电波传播，该组数据的环境特征定义为零向量. 若测量数据是NLoS径，则基站和接收机之间的地物类型影响电波传播，其环境特征的定义如1.2节所示.

结合提取的新环境特征和测量信息构建新网络数据集，其中对应BS2和BS3的数据集作为训练集，对应BS1的数据集为测试集. 由训练集训练3.2节的神经网络架构建立路径损耗模型，对测试集进行预测，测试结果的ME、STD和Corr分别为0.96 dB、7.64 dB和0.76. 由此可知，在保证路径损耗模型预测足够准确(ME＜1 dB)的条件下，提取的新环境特征可进一步提升基于MLP神经网络的路径损耗模型的稳定性和泛化能力.

5 结 论

本文探究了基于MLP神经网络的路径损耗模型. 利用有限的环境类型，提出了表征电波传播环境的简易方法. 该方法避免了繁琐的三维场景建模，有助于提升路径损耗模型的效率. 结合采集的测量数据和提取的环境特征进行模型验证，结果表明：1) 与AB模型和CI模型相比，提出的模型能够实现路径损耗的准确预测；2) 环境特征的引入有助于MLP神经网络自动学习场景与电波传播之间的映射关系，提升基于MLP神经网络的路径损耗模型的性能；3) 结合LoS和NLoS标签提取的新环境特征，能够降低引入干扰地物的风险，提高基于MLP神经网络的路径损耗模型的稳定性和泛化能力. 综上，在大规模复杂场景和缺乏精准的三维场景信息的条件下，MLP神经网络能够自动从有限的地物类型中学习电波传播特性，建立准确高效的路径损耗模型.