面向无线光通信的大气湍流研究进展与展望
柯熙政 吴加丽 杨尚君
(1.西安理工大学自动化与信息工程学院,西安 710048;2.陕西理工大学物理与电子学院,汉中 723001)
引 言
无线光通信是以光束作为信息载体进行语音、数据、图像等信息传递的技术[1-2]. 早期的无线光通信可追溯到我国的西周时代,19世纪80年代贝尔发明了“光电话”才标志着无线光通信时代的来临[3]. 在第二次世界大战期间,无线光通信发展演变为红外线电话[4]. 1960年激光器的问世为无线光通信的发展提供了新的机遇[5]. 大气湍流会导致激光相干度蜕变、强度衰减、光束发散、光斑抖动等. 因此,深入研究大气湍流对无线光通信的影响十分重要[6-14].
1 大气湍流效应研究进展
人们对光在大气湍流中的传输研究经过了如下三个阶段:
1)起初人们建立了几何光学近似法、Rytov近似法等方法[15]. Tatarskii借鉴Kolmogorov和Obukhov的湍流理论,采用Rytov近似法将电场写为指数形式,简化了求解振幅和相位起伏的过程,解释了光波在湍流介质传输时观察到的实验现象[16-17].
2)随后人们发现了许多新的实验现象,如光波起伏的饱和效应和涨落现象等[15]. 为了更好地解释这些现象,人们提出了如Markov近似法[18]、启发式理论[19]、费曼路径积分法[20]以及相位屏理论[21]等强起伏理论. Markov近似可以很好地处理强湍流中光的传输问题,但在中等湍流时仍然没有很好的处理方法[22-24].
3)之后人们的研究开始集中于高阶矩的求解.Wilbur采用阶梯近似法推导出波在随机介质中传输的二阶矩[25],Filinov利用Monte Carlo方法分析了场的闪烁指数、二阶矩和四阶矩[26],Xu则利用积分方程迭代方法讨论了大气湍流二阶矩解[27].
由于二阶矩无法精确描述光的传输特性,而高阶矩可分别给出分布宽度以及偏离对称性的信息.为了更准确地研究光波在大气中的传输特性,就需要顾及概率密度函数末尾的部分信息,这就要求研究其高阶矩. Lee通过研究得到高阶对称矩的高斯解[28],Ito对光束的传输特性进行了研究,最高研究到十阶矩[29],但这些工作并没有得到对应高阶矩表达式. 吴健通过求解前向多重散射m+n阶矩方程,进而导出了一、二以及四阶对称矩的表达式[30]. 李桂珍等人推导出2n阶对称矩的一般表达式,求出了采用二阶矩表示的双频、双点互相干函数的解析解[31]. 李晓庆等人推导出了光束的一阶、二阶、三阶以及四阶强度矩表达式,并以高斯光束为例讨论了光束平整度参数K在大气湍流中的传输规律[32].
人们对光束的扩展和光强的闪烁特性的研究涉及较多. Whitman等人采用标量波动方程分析了光在随机介质中传输的扩展现象[33]. Poitier应用Born近似讨论了湍流中聚焦波束的展宽现象[34]. R.L.Fante利用修正Von Karman谱获得了光束长期扩展公式,用互相干函数获得了短期光束扩展公式[35]. 范承玉利用昆明地区大气湍流强度的数据计算了不同高度下的光束扩展状况[36]. Andrews等人研究了湍流内尺度和外尺度对长期光束半径大小的影响[37-41];韦宏艳等人对斜程传输路径情形激光波束的扩展半径进行了分析[42]. 郭立新等人在根据ITU-R提出的湍流大气结构常数模型,分析了大气湍流闪烁指数的变化规律[43-44]. 吴振森[45]、韦宏艳[46]等人讨论了斜程高斯波束的闪烁指数特性. 张逸新等人分析了湍流外尺度影响的光束短期扩展因子和高斯光束等效半径与传输距离、初始光束半径、光波波长间的关系[47]. 张飞舟等人研究了光斑碎斑对光束扩展的影响,发现随光束质量变差和湍流强度的增强,总光斑扩大、碎斑数目增多、占空比减小[48]. Andrews等人根据Kolmogorov谱推导了平面波、球面波、高斯波束的光强闪烁特性[49]. 张晓欣等人推导出了部分相干平顶光束在大气湍流中斜程传输时的均方根(rootmean-square, RMS)束宽表达式[50]. 段美玲等人研究了斜程在大气湍流中厄米高斯光束的扩展[51].
2 大气湍流及其效应
2.1 湍流
流体运动有层流和紊流,紊流属于不规则运动,层流属于规则运动[52-53]. 大气湍流中每一点的压强、温度、速度等物理量均存在随机涨落. 大气湍流的发生需具备一定的动力学和热力学条件,当上层空气温度低于下层的对流条件对形成大气湍流最有利.大气湍流由各种不同尺度的旋涡叠加形成,旋涡尺度较大者可达数百米,旋涡尺度较小者约为数毫米.湍流漩涡无法保持稳定状态而分裂成小漩涡,进而再分裂成更低一级的小漩涡. 当湍流漩涡具有的能量与其所具有动能相等时,便不再分裂了,此时蜗旋尺度最小,这便是内尺度l0.
通常用大气折射率结构常数C2n来量度大气折射率起伏,在均匀各向同性湍流中定义为[54]
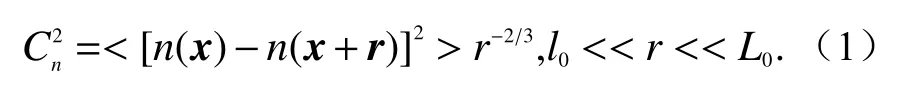
式中:n为大气折射率;x和r为位置矢量;r是矢量r的模;l0和L0分别是湍流的内尺度和外尺度.Cn2与大气状况以及所处的海拔高度相关. 作者认为折射率场是各向异性的,西安理工大学柯熙政教授团队目前也正在开展该领域的测量工作[55-56].
光在大气湍流中传输时会出现不同程度的光强衰减、光束扩展等效应[57]. 当湍流尺度远远大于光束直径时,湍流的主要影响使光束产生随机偏折;当湍流尺度与光束直径大小相当时,在光电探测器上像点会出现随机抖动;当湍流尺度远远小于光束直径时,光束截面内会包含很多小湍流涡旋,在接收面上会出现光强衰减、光束扩展. 如果这些湍流效应同时发生,会导致光传输效率大大降低,并且接收端的光斑 波前会发生畸变,光束质量也会变差[58-60].
2.2 湍流的形成
大气湍流具有随机性和非均匀性[61-63]. 大气湍流发生在大气底层的边界层内、对流云的云体内部、大气对流层上部的西风急流区内. 近地表面对气流拖曳引起的风速剪切、太阳辐射对地表不同位置加热的差异以及地表热辐射导致的热对流等过程,会造成大气温度和速度场的随机改变. 大气温度的随机变化又会导致风速的变化,使得大气密度和大气压出现随机变化,从而产生大气湍流[64-66]. 大气湍流的存在使得大气中的动量、热量、水汽等方面的交换作用显著增强,还会造成大气折射率的随机起伏.其起伏特性主要与大气的温度、湿度以及风速剪切不稳定性等有关[67]. 大气湍流所产生的涡旋元会随风的快速运动而不断产生和消失[68]. 涡旋的产生、变小到消失,这一过程不断重复,运动之间相互叠加,形成随机的湍流运动,即为大气湍流[69-72].
2.3 雷诺数
1883年,雷诺将水从左端注入一个玻璃圆管中,在管的入口处滴入少许经染色的液体以便观测到液体的流动. 实验发现:如果水流动速度足够慢,带颜色的液体由注入处到玻璃管出口处将维持一条完整直线而不会扩散;但当水的流速增大且超过某一阈值时,带颜色的液体就会很快分裂,明显与周围之前未着色的水流混合,到管出口处时玻璃管中的水颜色已变淡,也没有明显的界限可分出带颜色和不带颜色的水流. 带颜色的水流和周围水混合之后的状态是很不规则的,其运动也变得混乱没有规律,随机性增强,将流体的这种运动称为“湍流”. 而之前未相混合的细流,其染色之后的液体形成的流线平滑而笔直,称为“层流”. 雷诺指出流体总是在相同的雷诺数下从层流转向湍流,有关实验也表明随机性湍流是有规律的层流在流速增大时所形成的[73].
大气湍流运动可视为各种尺度的涡旋连续分布叠加而成,雷诺数可表示为动能和耗散能之比[74]:

式中:ρ代表流体密度;υ代表流动流体的特征速度,当流体运动为层流状态时,它即为流动流体的速度;L为整个流体的特征尺度;v=μ/ρ代表流体的运动粘性系数,其量纲为m2s-1;μ代表流体本身的粘性系数,其量纲为ms-1l-1. 雷诺数自身没有量纲. 存在一个临界雷诺数Rec,当Re<Rec时,大气流动为层流运动;当Re>Rec时,大气流动为湍流运动,如图1所示.
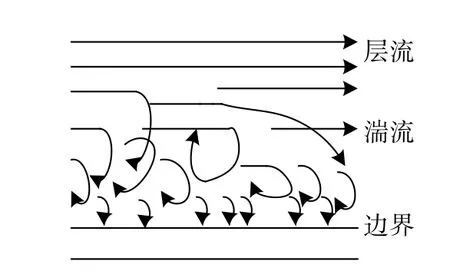
图1 层流湍流示意图[73]Fig. 1 Schematic diagram of laminar turbulence[73]
用雷诺数判断湍流也可通过惯性力和摩擦力之间的相互关系来解释. 当Re较大时,湍流受惯性力的影响大于摩擦力,这时湍流自身所具有的能量持续转移给扰动运动,从而形成大气湍流. 假设ε为湍流在单位时间内单位质量所耗散的平均能量大小,Wk为湍流在单位时间内单位质量的平均动能大小,τ是和湍流相关的特征时间,τ~l/V,则能量E随时间的变化可表示为[75-76]:
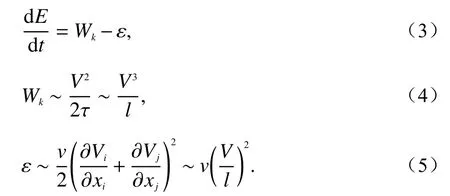
式(3)为湍流能量的平衡方程. 当Wk<ε时,dE/dt<0,起伏不断减小,趋于消失,大气运动不会形成湍流;当Wk=ε时,能量E为常数,大气运动形成稳定状态的湍流;当Wk>ε时,dE/dt>0,当扰动能量增加,运动将不稳定.
对于边界层的湍流,雷诺数非常大,通常在106~107范围内. 当Re>>Rec时,流体的运动完全随机,不再受初始条件影响. 同时,Wk>>ε,几乎所有动能都是由大尺度湍流传给小尺度湍流.
2.4 湍流的内、外尺度
外尺度为L0的涡旋本身具有很大的起伏能量,这即构成了最初的湍流能量. 为研究涡旋的流动特性,特引入内雷诺数R el,其为能量转换率和能量耗散率之比[77]:

式中:l为涡旋流动的特征尺度;v1是与特征尺度相当的起伏速度. 这个巨大涡旋的内雷诺数会随着流体流动雷诺数的增加而增大,当 R el大于某一个临界值时,该涡旋本身将会呈现不稳定性,从而分裂成比较小的涡旋,将能量传送给这些小涡旋. 如此继续,涡旋具有的特征尺度会变得越来越小,对应的内雷诺数也会变小[78]. 直到内雷诺数趋于某一数值,流体的粘性成为影响运动本质的决定性因素,动能全部转化为热能而且无法再分裂成更小涡旋,此时,最小涡旋的特征尺度l0即为湍流的内尺度,内尺度一般在毫米量级. 图2给出了湍流能量转换的示意图.
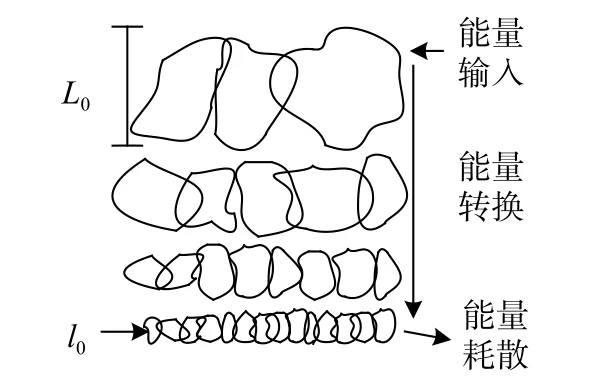
图2 湍流能量转换示意图[79]Fig. 2 Schematic diagram of turbulent energy conversion[79]
2.5 湍流的特性
大气湍流是具有以下特性的杂乱无章运动:
1)大气湍流是在外力的作用下产生的一种运动方式,随着外力的增加,流体的运动状态由层流变为湍流,运动逐渐失去稳定性,变成不规则的、杂乱无章的非线性运动.
2)虽然湍流运动是一种不规则运动,但其相邻空间点上的运动参数具有一定的相关特性,可以采用统计平均法等统计规律对湍流进行分析.
3)洛伦茨指出大气湍流对初始条件敏感,贝里以精确数值计算结果对洛伦茨断言进行证明,得出大气湍流对初始条件具有敏感依赖性[79].
2.6 大气折射率结构常数
大气湍流是各向异性的,但在给定的足够小区域内可近似视为局域均匀各向同性. 在此前提下,大气折射率分布满足Kolmogorov提出的大气折射率结构函数Dn(r)的“2/3定律”[80]:
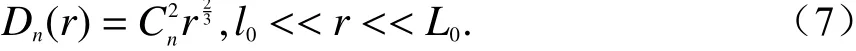
式中:r为统计湍流特性两点间距离;l0、L0分别为湍流的内尺度和外尺度.
当所研究的空间尺度小于湍流内尺度l0时,粘性耗散对大气起伏影响起主要作用,抑制了湍流的进一步发展;当空间尺度大于湍流外尺度L0时,气流惯性力对大气起伏特性影响起主要作用.
大气折射率结构常数Cn2是大气光学中的基本参数之一,由于斜程传输路径上大气折射率结构常数是不均匀的,其大小随着高度的变化而变化;水平传输时则对大气折射率结构常数一般取某一典型值.因此,要对光束在大气湍流中的传输特性进行研究,大气折射率结构常数是必须解决的问题.
大气湍流可分为两类:一类是“边界层”湍流,受地面状况影响较大,厚度大约为数十米到数百米;另一类是“自由大气”湍流,基本不受地面影响. 两层之间的边界会受到地理环境、宏观气象条件、地面状况等多方面因素的影响.
“边界层”湍流主要受地表温度、湿度、压力等的影响. Wyngaard等人证明了在边界层内大气折射率结构常数随高度成-3/4次方的关系,这是一个半经验理论,但-3/4次方关系能够很好地描述地面上百米上空的大气折射率结构常数的变化规律[81]. 后来Neff用声雷达测定的Cn2随高度变化的实验也验证了Wyngaard理论中的-3/4次方的关系[82]. Kukharets和Tsvang之后提出指数模型来描述大气折射率结构常数[83].
大气折射率结构常数Cn2除了随高度变化外,在一天内的波动也很明显. 图3 为1971年7月15日科罗拉多州布尔德附近落基山脉距离地面2 m处的一昼夜24 hCn2特性的例子.
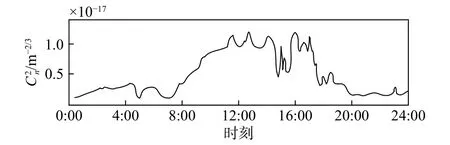
图3 Cn 2在晴天的24 h特性[84]Fig. 3 24-hour characteristics of Cn 2 on a clear day[84]
Hufnagel根据Ochs测量的3.2 km高度以下的大气折射率结构常数的实测数据,给出了一个在3~24 km范围内适用的Cn2经验公式[85]:
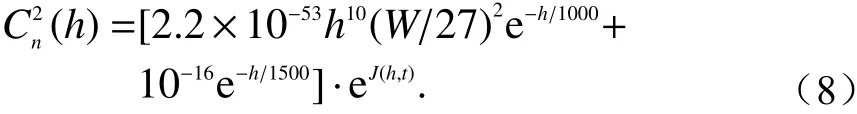
式中:J是一个零均值的均匀高斯随机变量,其相关函数为[86]
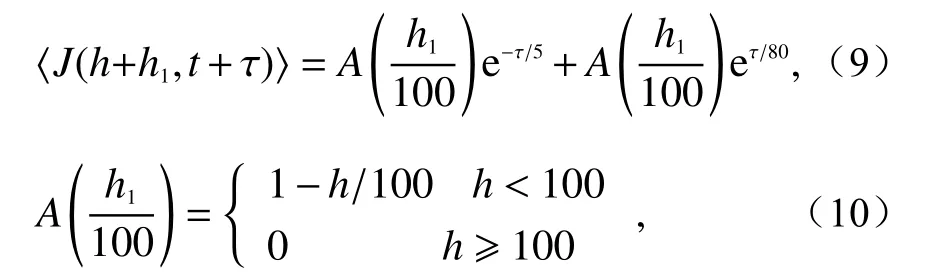
h为高度;τ为时间间隔;函数W表示高度在5~20 km的RMS速度,

υ(h)是该高度上的风速. Hufnagel[85]提出的W典型数据的均值为27 m/s,标准差为9 m/s. ITU-R颁布了新的大气结构模型,该模型使得从理论上分析光波斜程传输时成为可能[87]. 图4为ITU-R颁布的大气折射率结构常数随高度变化图,可以看出大气折射率结构常数Cn2随着高度的增加逐渐减小. 在1~4 km时,大气折射率结构常数基本不受风速和地表处Cn2(0)的影响;高于10 km时,主要受风速的影响[88].因此相应的经验表达式为
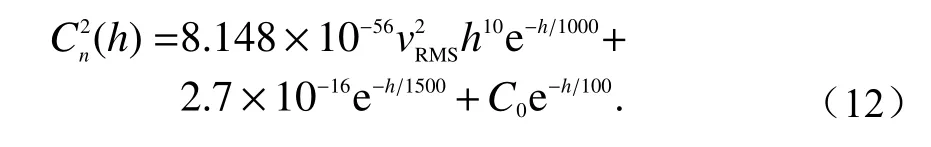
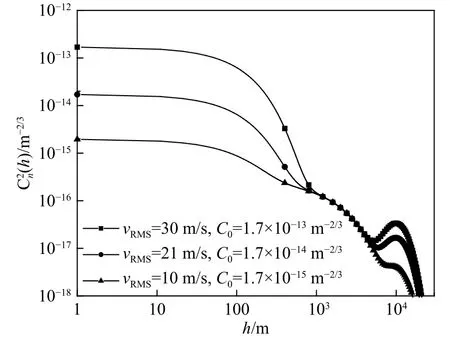
图4 大气折射率结构常数随高度h的变化Fig. 4 Atmospheric structure constant vs. height h
3 大气湍流折射率起伏模型
光波在大气中传输时,会受到大气折射率的影响. 单一的大气折射率和真空的相差不大,但其累积作用却不容小看. 设湍流尺度为r,根据湍流的内外尺度将湍流分为三种区域[89]:
1)输入区. 该区域中,κ为湍流空间波数,κ<2π/L0,由于风切变和温度梯度,造成能量输入给湍流. 该区域中谱的形状取决于特定的湍流是如何发生的,而且随机介质的特征物理量一般是非均匀、各向异性的. 由于湍流谱与大气湍流产生方式有关,目前还没有一种普通公式描述其湍流特征.
2)惯性区. 该区域中,κ>2π/L0,雷诺数较大,湍流涡旋的动能超过粘性耗散,因而运动过程不稳定,形成大气湍流. 此时,功率谱Φn(κ)的形状由制约着大湍流涡旋破碎为小涡旋的物理定律决定,该区域内湍流本质是各向同性的.
传统高斯谱和指数谱在惯性区不能全面反应光束传输及散射现象,Kolmogorov提出了Kolmogorov谱模型,如图5所示[90-93],表达式为
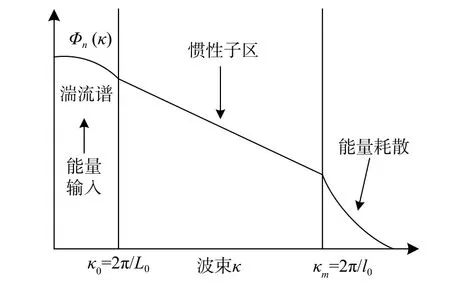
图5 湍流的Kolmogorov功率谱[93]Fig. 5 Kolmogorov power spectrum of turbulence[93]

该谱模型的缺点是当波数κ→0时,κ-11/3→∞,会出现Φn(κ)→∞的不合理结果.
3)耗散区. 当波数κ增大到另一个临界值κm=2π/l0,即κ>2π/l0时,功率谱Φn(κ)的形状发生改变. 该区域中雷诺数很小,湍流涡旋的粘滞性耗散能大于动能,因此,谱是极小的. 耗散区域内采用Tatarskii谱模型来描述:
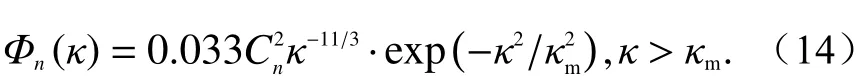
式中,κm= 5.92/l0. Tatarskii谱模型将湍流内尺度考虑进去,在波数较大的区域存在高斯函数的衰减因子,因此,可解决Kolmogorov谱存在的不合理结果. 这两种谱模型由于原点处都存在不可积的极点,仍然不能普遍使用. 因为在实际中地球大气层是有限的,当κ→0,Φn(κ)不可能接近∞. 以上两种湍流谱的应用还是存在一定的局限性,且Tatarskii湍流谱至今未得到实验结果的验证. 为了克服以上两种谱模型存在的缺点,在1948年,Von Karmon将湍流谱模型在耗散区功率谱近似表示为[94]
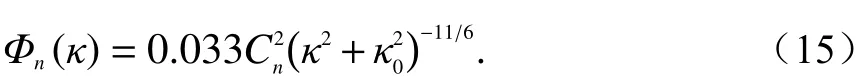
式中,κ0= 2π/L0. 随后,人们又将湍流的内外尺度均引入到该谱模型中,提出修正Von Karmon谱或指数模型谱[95]:
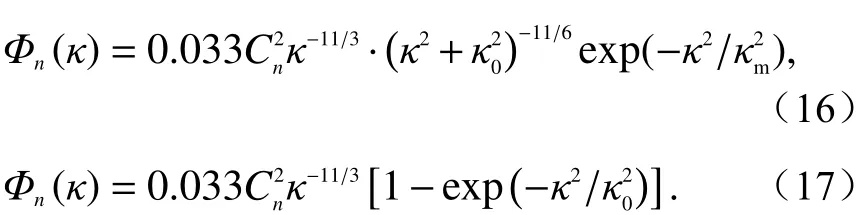
在大气边界层,我们需要考虑高度、边界层厚度、地面非均匀尺度等,这是Von Karman谱所不能描述的,Kaimal等人证明了这一点[96-97].
同时考虑到大、小尺度湍流起伏时使用广泛的是Tatarskii谱和Von Karman谱的综合谱,又被称为Von Karman谱:
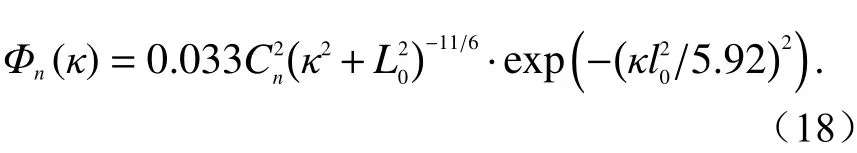
当κ0= 0时,Tattaskii谱也称为修正 Kolmogorov谱. 式(15)和式(16)这两个谱都没有包含高波数区突变因素,不能真实反映谱的实际特性,这时Hill提出了一个数值模型[98]:(
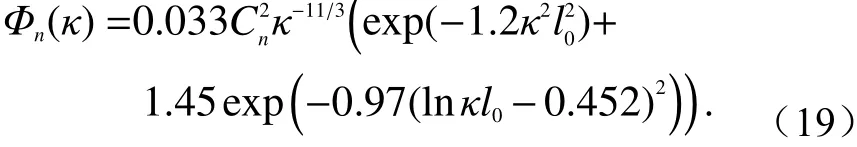
Tatarskii谱也与Von Karmon谱有一共同的缺点,均没有将影响光传输的高波数区突变因素考虑在内. Andrews和Hill在实验的基础上,得到一个数值模型[99]:
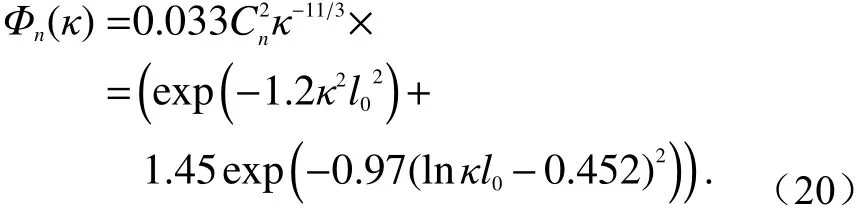
该模型形式较为复杂,Andrews又通过数据内插等方法提出修正Hill谱模型[100]:
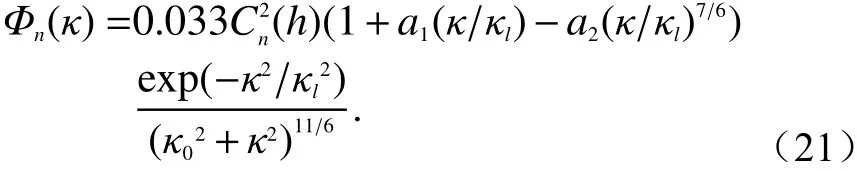
式 中:κl=3.3/l0;κ0=2π/L0;a1=1.802;a2=0.254. 式(21)当用a1=a2=0和κl=κm作代换后,即可简化为Von Karmon谱模型;当κl=l0= 0时,可退化到Kolmogorov谱模型.
由于Tatarskii谱模型在耗散区的形式与实际情况不符,Hill又提出了适合湍流耗散区的谱模型,但在该领域一直未得到普遍认可. 人们常用的是T atarskii和Von Karmon谱模型.
3.1 光束漂移
如图6所示,无线激光通信系统由发射天线与接收天线两部分组成,发射天线与接收天线通常选用卡塞格林望远镜,其光学结构可简化为单透镜系统.
从图6可以看出:

图6 光斑漂移对无线光通信系统的影响Fig. 6 Influence of spot drift on wireless optical communication system
1)忽略大气湍流时. 发射光束传输到接收光学天线的接收面上,其主光轴与接收天线视轴重合,通过接收光学系统将光束焦点汇聚到通信探测器的接收端. 分光棱镜将接收光路一分为二:一束用于通信探测,另一束用作光斑位置检测. 通过四象限探测器接收面上的光斑位置,可以得到光斑在四象限探测器的中心位置,光斑中心与四象限探测器中心重合[101].
2)考虑大气湍流时. 光束在传输过程中由于受大气湍流的影响而发生漂移,导致光束在垂直于光轴方向发生随机移动而偏离接收面. 此时发射光束的光轴不再与接收天线的视轴重合且存在夹角,这就使得通过光学天线汇聚的光束焦点发生偏移,偏移的焦点不再入射到通信探测器的接收面上. 此时通信探测器接收的光束功率会大幅降低,不利于系统通信. 通过四象限探测可以检测到光斑质心相对于四象限探测器的中心位置偏移量;随着湍流的进一步发展,发射光束有可能会完全漂移出接收天线的接收面,无法汇聚发射光束,会造成通信链路的中断[102].
3.2 光束扩展
如图7,F0是发射平面处的波阵面曲率半径,F0=∞、F0> 0和F0< 0分别对应准直、聚焦和发散光束,实验中光束通常选择准直或聚焦光束.
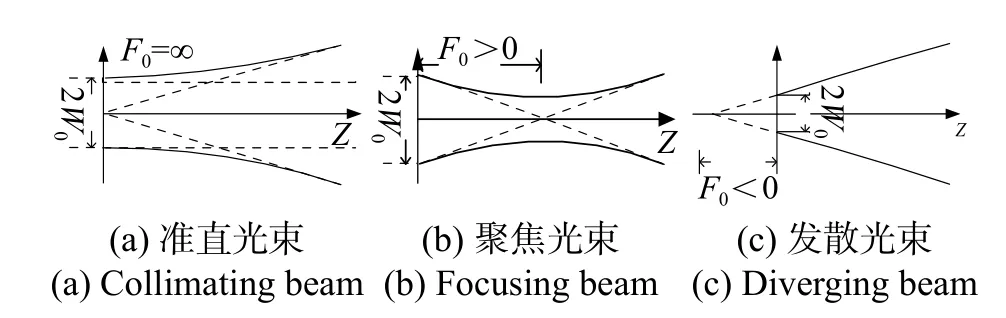
图7 不同光束示意图Fig. 7 schematic diagram of different beams
如图8所示,无线光通信系统中,当激光光束在理想状态下传输时,经耦合透镜聚焦到光电探测器表面,再进行光电转换得到电信号. 理想状态下所得到的光斑如图中光斑1所示. 当在大气湍流中传输时,受大气折射率起伏的影响,光束会产生扩展,同时光束横截面的能量降低,导致一部分光束不能通过耦合透镜到达光电探测器表面,如虚线表示的光束部分. 接收面上所得到的光斑如图9所示,大气湍流使光斑半径变大且光束能量降低[18].

图8 光束扩展、闪烁对大气激光通信系统的影响Fig. 8 Effect of beam expansion and flicker on atmospheric laser communication system
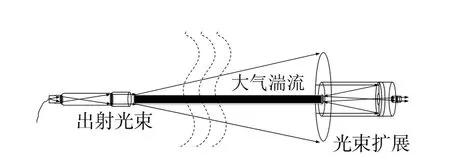
图9 光束扩展示意图Fig. 9 Schematic diagram of beam expansion
如图10所示,如果在接收平面上取很短的观察时间,可以看到一个半径为r1的被加宽的光斑偏离了原点r2的距离即为光束漂移量,而取的时间足够长,会看到光斑的随机游动会产生一个均方半径r3的大光斑,前者叫做短期光束扩展,后者叫做长期光束扩展[103-104]. 光束扩展是指由湍流涡旋引起的接收平面上的光斑半径或面积的变化. 当光通过小尺度涡旋时会产生衍射效应,导致光束扩展;反之光通过大尺度涡旋时会发生折射现象,引起光束漂移[105-107].
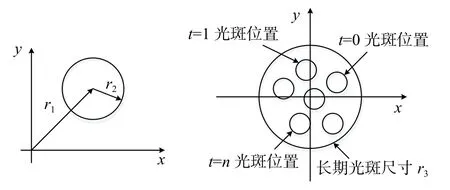
图10 接收面上光斑示意图Fig. 10 Schematic diagram of receiving plane spot
3.3 光强闪烁
如图8所示,当光束直径远远大于湍流尺度时,光束截面内会包含多个湍流涡漩,每个涡漩各自对照射在其上的光束产生独立散射和衍射,引起探测器平面上光密度在时间、空间上发生连续的变化. 若在湍流大气中与光源相距一定距离处测量光的强度,会出现光强随时间变化且围绕平均值作随机起伏. 闪烁大小与湍流强弱直接相关,光强闪烁效应会使通信系统误码率(bit error ratio, BER)增加[108-111].
3.4 到达角起伏
如图11所示激光在均匀介质中传输具有均匀波前. 在湍流大气中传输时,光束截面内不同部分的大气折射率的起伏将导致光束波前的不同部位具有不同的相位变化[112-113].
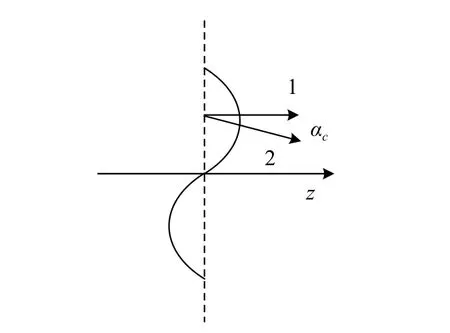
图11 局部到达角示意图Fig. 11 Schematic diagram of local arrival angle
如图12所示,大气湍流可能引起激光功率衰减、脉冲展宽等,导致通信系统信噪比(signal-tonoise rate, SNR)下降,BER升高. 部分相干光与完全相干光相比,可以抑制光斑漂移、强度闪烁以及到达角起伏.
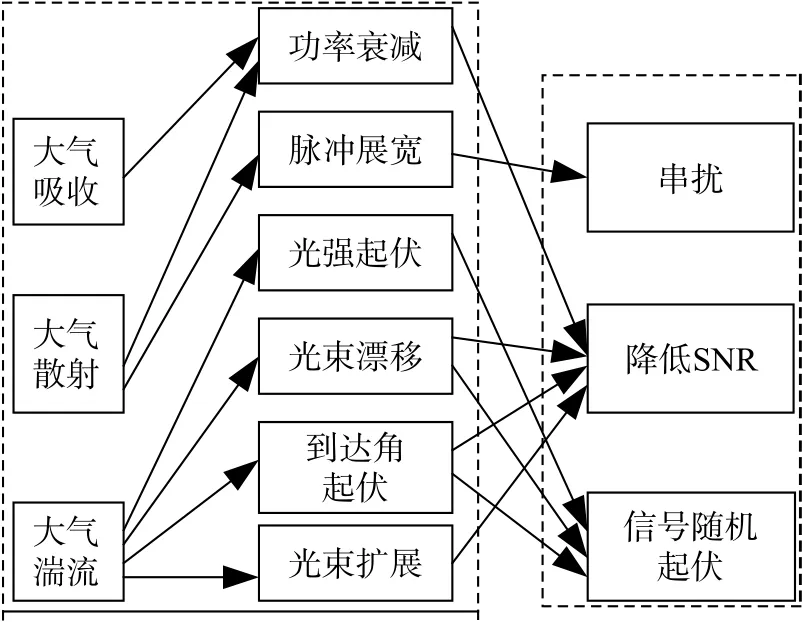
图12 大气湍流及其对光通信的影响Fig. 12 Atmospheric turbulence and its influence on optical communication
4 大气湍流中光传输的分析方法
随机介质中激光传输采用的主要计算方法有:
1)对随机介质介电常数和辐射场做微扰近似处理,带入波动方程计算得到辐射场分布.
2)首先对随机介质中介电常数的统计特性进行假设估计,然后构建和求解辐射场统计矩方程.
3)采用波动方程对多次散射的结果进行直接数学 计算,此方法计算相对困难[114-116].
4.1 Rytov近似
大气湍流的时变特性使得对于某一固定时刻和固定位置的介电常数εr进行直接描述并不现实,通常采用空间变量R和时间变量t的随机函数来描述大气湍流中介电常数的统计特性[117]:

假定εr只随空间变化,即光波保持单一频率,不考虑频移或频谱,那么

采用折射率n的Maxwell方程可写成
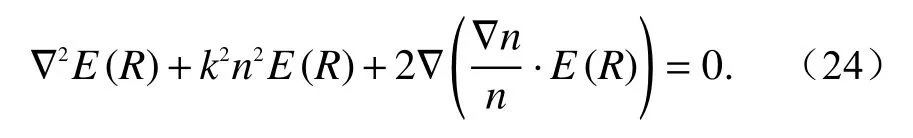
忽略去极化效应后式 (24) 中第三项可省略,假设U(R)为与z轴垂直方向传输的电磁场E,则随机介质中的电磁波传输波动方程为
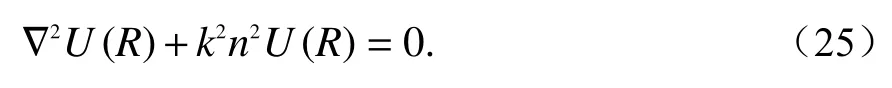
弱湍流时,电磁场可以表示成:
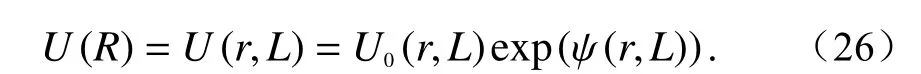
式中:U0(r,L)是静态无湍流条件下无相位扰动的散射场;ψ(r,L)是由于湍流引起的复随机相位扰动. 对复扰动相位进行展开有
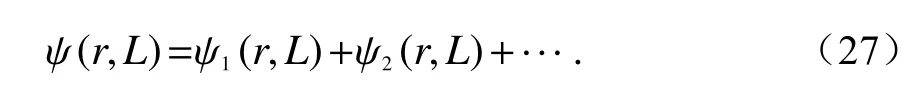
式中,ψ1(r,L)、ψ2(r,L)分别为一阶和二阶复相位扰动近似.
我们给出三个基础性统计矩的定义[118]:
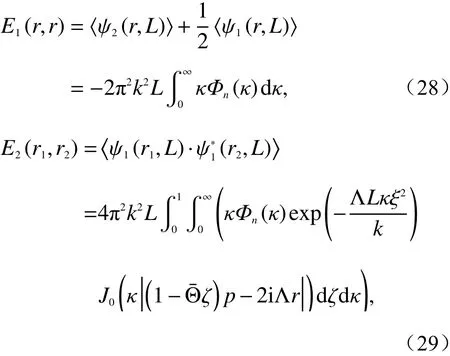
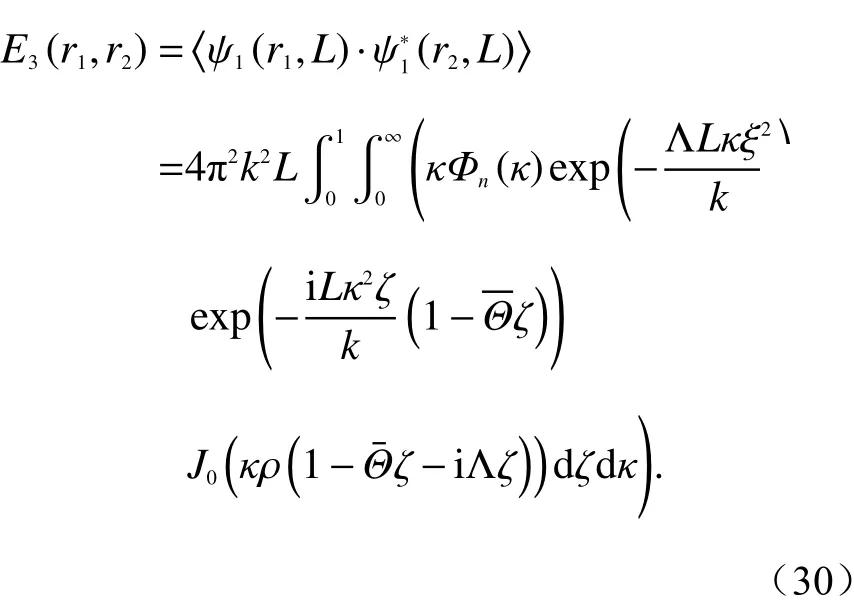
式中:r1、r2分别表示在z=L处的横平面内任意位置的两个点;p=r1-r2;ρ=|p|;ζ=1-z/L;Φn(κ)是折射率空间谱密度.
对于平面波的Rytov方差 σ2R, 通常受波长、传输距离以及大气折射率结构常数影响,且有

由于多重散射效应随着Rytov方差的增大逐渐增强,因此传统的Rytov近似计算方法在强湍流条件下并不适用. 因此Andrews等人在此基础上提出了修正Rytov近似. 假设:1)大气湍流并不具有均匀的统计平均特性;2)由于湍流具有传递特性使得大尺度涡旋带动了小尺度涡旋在传输终端引起光强闪烁,因此光强闪烁同时受大尺度涡旋和小尺度涡旋的影响;3)大、小尺度湍流对光强闪烁具有统计独立的影响;4)采用空间滤波技术使得光波经过强湍流后光强闪烁的求解可使用Rytov近似方法;5)采用几何光学的方法研究大尺度湍流的光强起伏. 因此修正的Rytov方法使得适用于弱湍流的Rytov方法在强湍流条件下仍可使用,因此光波强度的方差可表示成[119-120]:

式中:σx2是x的归一化方差;σy2是y的归一化方差.为了计算方便取<I>为1,此时光强的起伏方差表达式为
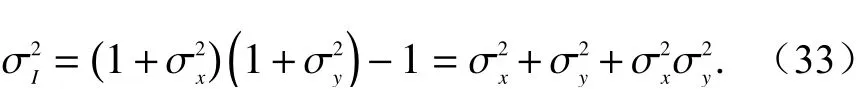
在弱湍流区使用的Rytov近似中,距离光源L处的式(26)对应的Rytov解只适用于单次散射区域,因此需要对多重散射区的Rytov近似进行修正,修正后的公式为
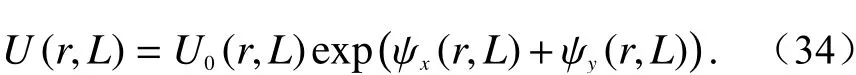
式中,ψx(r,L)、ψy(r,L)是统计独立且不相关的受大气湍流影响的复随机相位,即分别是大尺度和小尺度湍流产生的影响. 式(34)中,指数项的求和即大尺度湍流和受大尺度湍流调制的小尺度湍流,将大气湍流作为空间滤波函数,有
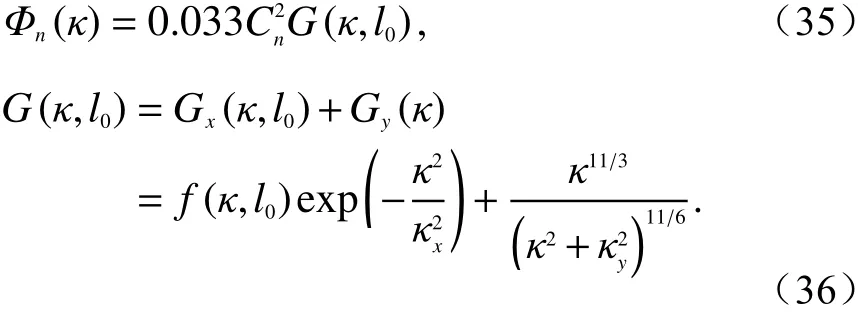
式(36)中,κx和κy分别是大尺度湍流和小尺度湍流的空间频率. 滤波函数G(κ,l0)是低通滤波函数Gx(κ,l0)和 高通滤波函数Gy(κ)的叠加.
4.2 Markov近似


抛物线方程和马尔科夫近似成立的条件为:kl0>>1,kCn2L05/3<<1.
5 大气湍流抑制技术发展趋势
5.1 多光束传输技术
将多个波长相同的独立激光束由不同发射天线发出,并要求各天线间距S满足约束条件S2≥λL(其中λ代表激光波长,L为通信距离),在通信接收端进行激光光束的非相干叠加,采用该方法能够有效地抑制大气湍流所引起的光强闪烁,在接收端的光功率起到平滑作用,有效提高通信质量. 近年来,人们研究多光束传输技术用于对IM/DD光通信系统BER的改善,如图13为将多光束传输技术应用于通信距离100 km的相干光通信外场实验中,并结合实验结果分析了多光束传输技术对通信系统性能的改善情况.
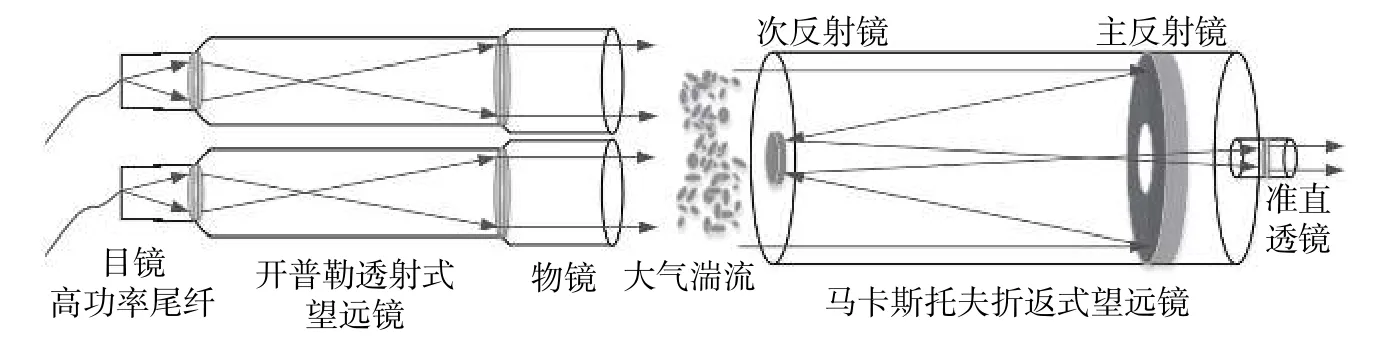
图13 2×1系统示意图Fig. 13 Schematic diagram of 2×1 system
我们在青海湖二郎剑景区至刚察县泉吉乡完成了通信距离为100 km的多光束传输实验,图14(b)是实验场地图.

图14 实验链路地图Fig. 14 Experimental link map
图15是系统采用单光束传输和两光束传输时接收端信号光功率起伏曲线,单光光束传输接收端平均光功率为-41.53 dBm,方差为6.01 dBm2;两光束传输时接收端平均光功率为-33.47 dBm,方差为3.79 dBm2.采用两光束传输时系统可以有效降低接收端信号光功率的抖动方差.

图15 不同传输方式下信号光功率变化曲线Fig. 15 Curves of signal optical power simultaneous interpreting under different transmission modes
选取电子电量1.6×10-19C,量子效率0.8,普朗克常数6.626×10-34J·s,负载阻抗50 Ω,背景辐射功率10-9W,探测器带宽100 MHz,玻尔兹曼常数1.38×10-23J/K,环境温度300 K,本振光功率为1 mW,不同光束传输的外差探测系统SNR变化曲线如图16(a).单束激光传输时,系统SNR均值为33.44,方差为6.01;两光束传输时,系统SNR均值为41.5,方差为3.8,这表明采用多光束传输的技术可有效提高SNR均值,减小SNR波动范围.
大气激光通信系统采用不同数目的光束进行传输后,通信系统的BER曲线如图16(b)所示. 可以看出:单光束传输时系统BER均值为6.5×10-9,方差为3.14×10-7;两光束传输时系统BER均值为9.98×10-11,方差为1.95×10-20,相较于单光束传输,两光束传输可使系统BER均值和方差值降低3个数量级,更好地改善了通信系统性能.
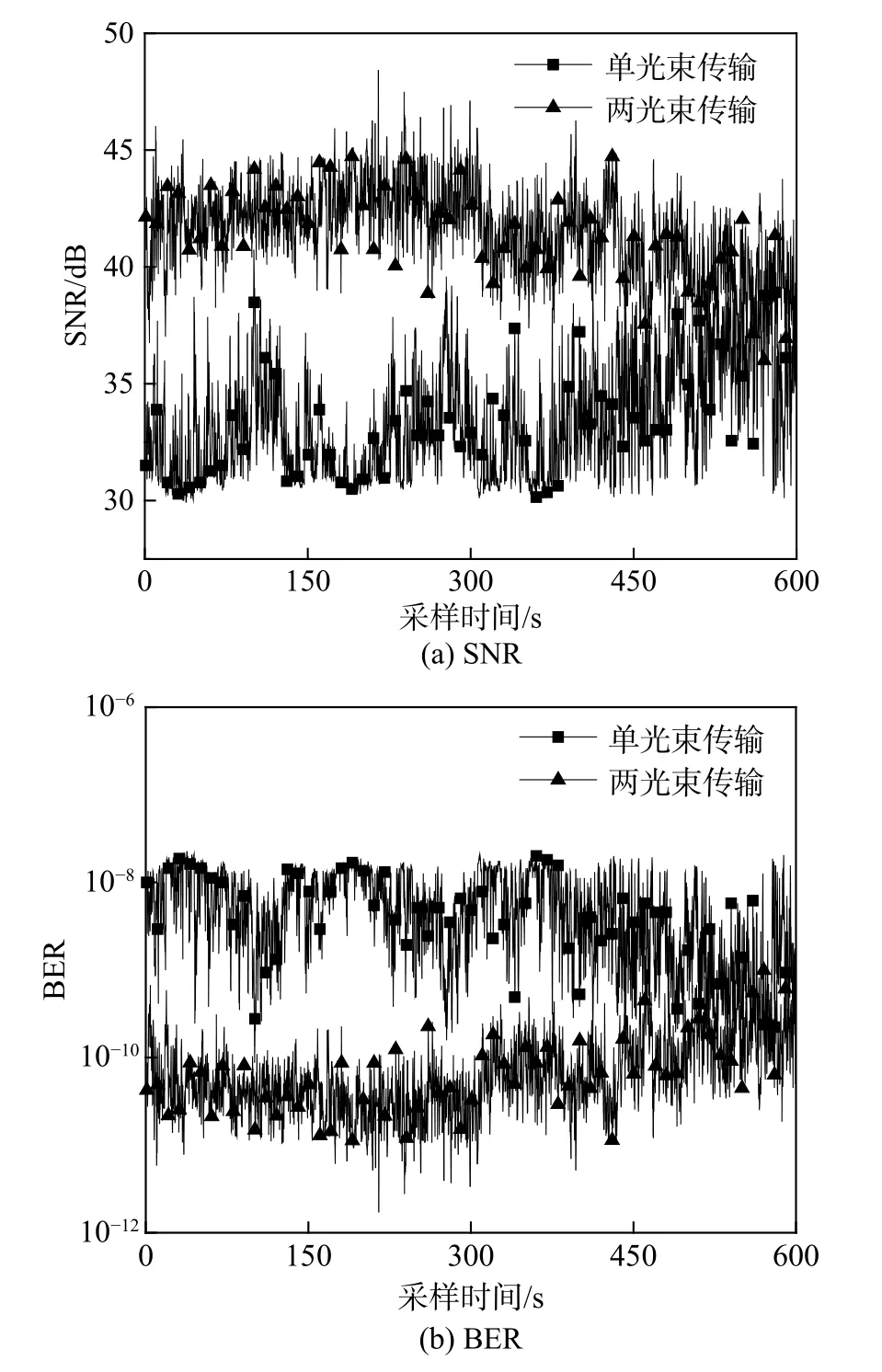
图16 不同传输方式SNR和BER曲线Fig. 16 SNR and BER curves of simultaneous interpreting systems under different transmission modes
5.2 自适应光学波前校正技术
激光经远距离传输后受大气湍流的影响波前产生畸变,这会直接导致无线激光通信相干检测中的耦合效率以及混频效率下降,因此有必要对畸变波前进行修正. 畸变波前相位通常可以根据zernike多项式进行展开,其中倾斜分量称为低频分量,其余分量称为高频分量. 波前倾斜分量约占波前整体畸变量约86%,因此有必要使用多校正器的组合方式(如快速反射镜(fast steering mirror, FSM)和变形镜(deformable mirror, DM)的组合)进行波前校正.
使用FSM校正低阶像差,使用DM校正高阶像差,基于zernike多项式的正交性使得两者之间的校正区域空间具有明确划分. 基于二维运动的压电FSM与具有独立单元的DM69组成的自适应光学系统如图17所示. 光波经不同距离如室内、600 m、1 km、5 km、10 km及100 km传输后,分别测量波前峰谷(peak to valley, PV)值、zernike系数倾斜分量比例以及倾斜分量变化的方差,经计算处理后得到如表1所示数据. 图14为10 km和100 km的实验链路,其中10 km实验链路通信两端分别位于白鹿原和西安理工大学教六楼,100 km实验链路通信两端分别位于青海湖二郎剑和泉吉乡. 由表1可以看出:波前畸变量随着传输距离的增大而增大,倾斜分量比例占据了整体畸变量约80%;倾斜畸变的方差也随着距离的增大而增大,这表明变化的速度也会随着通信距离的增加而增大.
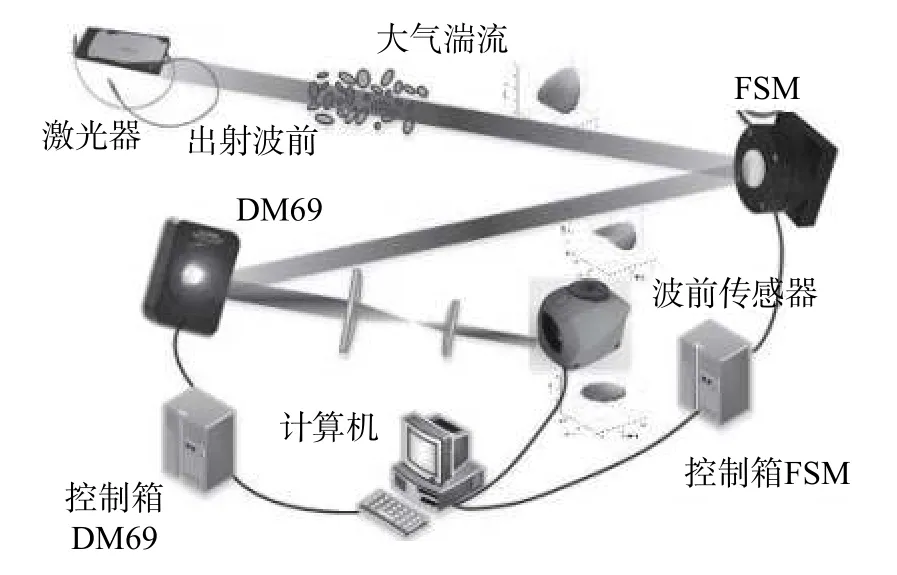
图17 基于FSM和DM组合的自适应光学系统Fig. 17 Adaptive optical system based on combination of FSM and DM

表1 不同距离下实测波前值Tab. 1 Measured wavefront values at different distances
图18为不同距离情况下实测的波前PV值,可以看出波前畸变程度以及波前变化速度都会随着传输距离的增加而增加. 当传输距离达到100 km时,强湍流导致光强闪烁使得采集的波前完全破碎,采样点不完整使得重构困难导致采集数据不连续.
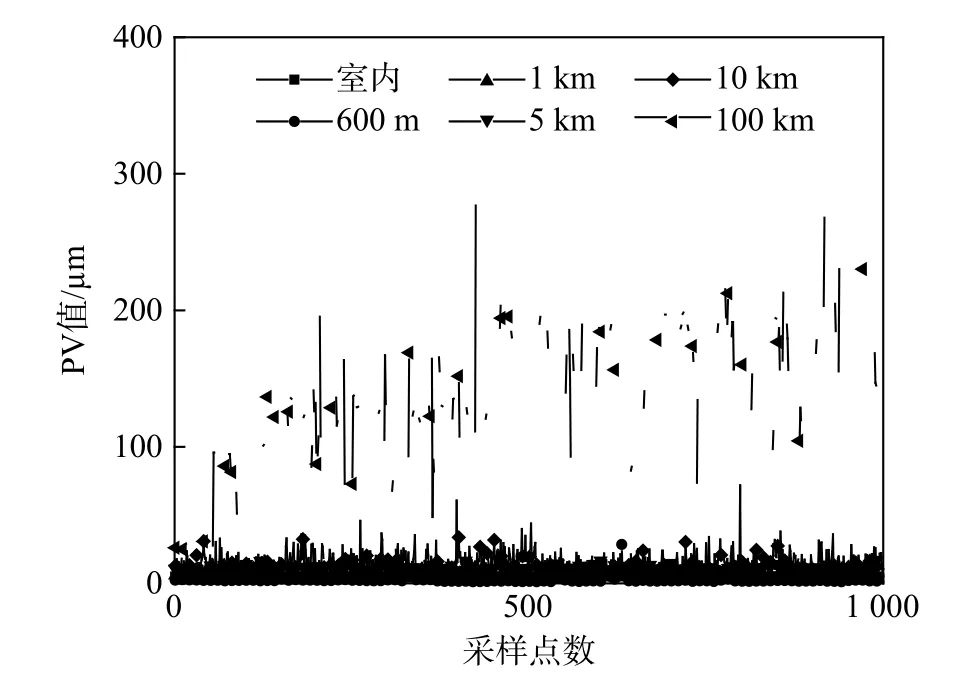
图18 不同距离情况下实测波前PV值Fig. 18 Measured wavefront PV value at different distances
图19为激光经100 km传输后,仅由FSM修正后、仅由DM修正后,以及FSM和DM同时修正后的波前相位图. 由图19可知:仅由FSM修正后,波前PV值由450 μm降至300 μm;仅由DM修正后,波前PV值降至300 μm;当FSM和DM同时修正后,波前PV值降至200 μm,说明基于FSM和DM组合的自适应光学系统的修正效果要优于单独FSM或DM的修正效果. 随着通信距离的增加,大气湍流强度增大,波前修正的效果变差. 这是因为波前修正的效果与波前传感器探测精度及本体噪声、波前重构精度、闭环带宽、大气测量环境状况等均有关系.
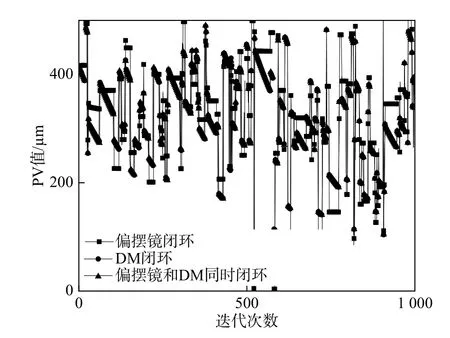
图19 100 km情况下波前校正PV曲线Fig. 19 Wavefront correction PV curve at 100 km
6 总 结
本文首先根据先前学者的研究对大气湍流研究进展进行了汇总,对大气湍流进行了详细的分析解释. 通过光束扩展、光束漂移、光强闪烁、到达角起伏等角度给出了大气湍流对激光传输的影响,对光波在大气湍流传输中理论的计算方法进行了讨论.最后作者给出了关于抑制大气湍流的一些方法设想,虽然该方法在理论分析和工程实际中略显不为成熟,但不失人们对于该领域的有益研究.

