考虑泄流效应的风电场并网点电压系统侧增援调控方法

于其宜，王 琦，汤 奕

（1. 东南大学电气工程学院，江苏省南京市210096；2. 南京师范大学南瑞电气与自动化学院，江苏省南京市210046）

0 引言

在发电侧能源结构转型［1-3］的背景下，中国在可再生能源发电技术上的快速发展使得电网中风电并网比例不断增大［4-7］。风能资源的有效利用缓解了电力紧张，但由于风速的不确定性［8-10］，风电场引起的公共耦合点（point of common coupling，PCC）处的电网无功电压等问题已不容忽视［11-13］。

针对PCC 电压问题，目前提出的方法主要分为机组级电压控制措施和场级电压控制措施2 类［14-20］。基于模型预测控制，文献［14］提出了风速波动前风电场有功和无功功率协调控制的方法。文献［15］利用风机和场内多无功源，提出了考虑风速波动的并网点及场内馈线电压的优化方法；基于改进粒子群算法，文献［16］对PCC 电压和网损优化实施优化；文献［17］从场群层、子场层、机组层3 个层面，基于遗传算法对风机承担的无功任务进行优化计算；文献［18］利用每台风机变流器的电压调节能力，设计了自适应下垂控制改善PCC 电压水平；文献［19］通过协调风力发电机组和静止同步补偿器，提出了一种基于对偶分解的分布式电压控制方案；文献［20］利用风电机组和站内无功源的无功调节能力，搭建了风电场电压管控平台。

以上文献表明，利用多无功源的协调控制（如场内的无功补偿装置、升压站内的变压器）以及风机变流器的无功控制能力即可实现PCC 电压调控。在不同的有功出力条件下，并网型风电场迟相运行时提供无功功率的能力或进相运行时对无功功率的需求差异性较大。尤其是在高功率因数运行状态下，风机自身的无功输出能力不足，易导致较大的无功缺额。

在实际工程中，不少风电场存在无功容量配比低于国家标准GB/T 19963—2011 的情况［21］，且存在部分无功容量配比达标的风电场受电网工况影响仍会出现自身无功不足的现象。针对以上问题，需要求助邻近的无功富余的变电站实施辅助性增援调控［22-25］。因此，系统侧常在风电场附近的变电站适度超额配置一定量的无功容量以备增援调控之需。

然而，实际中却常出现如下情况:在某邻近变电站实施增援调控的过程中，可能会出现补偿变电站及其周边少量节点电压过调越限的现象。究其原因在于，参与增援调控的变电站一般与PCC 存在一定的电气距离，且与系统侧其他负荷或电源节点间存在多种连接关系，相较于风电场侧的就地补偿，在增援调控变电站实施的异地补偿增发/减发的无功功率会出现一定程度的向非风电场方向“泄流”的现象。此现象严重时，必然会极大地弱化增援调控的能力。此时，若强行通过增加补偿量来提高对PCC电压的支撑效果，则很容易导致补偿变电站及其周边少量节点电压出现越限，从而呈现某种“顾此失彼”的不良态势。

针对上述问题，本文提出一种考虑泄流效应的风电场PCC 电压系统侧增援调控方法。所提方法的主要创新或特点包括:①基于泄流效应、无功裕度等影响变电站补偿效果的众多关键因素，建立了包含无功补偿增量泄流比、无功供给保障度、电压支撑度等在内的指标集，给出了待调控风电场周边变电站参与增援调控的基本条件及变电站优选方案；②研究参与调控无功补偿站的优选与PCC 电压增援调控任务分配问题，分别设计了启发式决策和考虑调控代价的优化决策方法，使参与增援调控的无功补偿站的补偿效果达到最优，从而解决了因风电场无功容量配置不足而导致并网点电压在某些运行工况下PCC 电压越限的问题；③相比于大系统的无功优化，结合问题特点选择线性规划模型的计算方案具有简便、高效的特点。

1 无功补偿增量的泄流效应与泄流比定义

一般就综合控制性能而言，以在目标电压待控节点实施就地补偿或调节为宜。然而在实际系统中，常常受多种技术、经济因素决定，导致待控节点的无功补偿容量或电压调节能力有限，在其优先使用并耗尽自身容量或能力的情况下，往往需要寻求周边邻近变电站（应为具有剩余无功补偿能力的变电站，下文将其统一简称为补偿站）的无功支援。

在电网拓扑差异和实际工况的综合作用下，在邻近无功补偿站通过自身无功补偿或电压调节系统增发（或少发）无功功率对待控节点实施增援的同时，因补偿站存在多回与其他节点相连的进出线而形成潮流多点分流作用，无功增量一般难以全额（甚至无法做到高额）流向待控节点，即会出现不同程度地向增援对象以外节点泄流的现象。泄流程度高时，除会导致待控节点被增援的效果严重变差以外，甚至还会引起其他非待控节点原先正常的电压态势出现异常情况。因此，有必要在决策增援方案时考虑无功补偿增量的泄流效应及其不良影响。

设在电网一定运行状态下，某邻近补偿站i增发无功功率ΔQi后能够流向待控节点j的量为ΔQi，j（参见图1），则可定义式（1）形式的泄流比αi，j，以量化站点i对节点j实施无功增援时无功补偿增量的泄流程度。

图1 补偿站无功补偿量泄流效应Fig.1 Drainage effect of reactive power compensation of substation

由式（1）可知:在αi，j等于某一数值的条件下，若补偿站i的无功增量为ΔQi，则能够流向并对待控节点j实施有效增援的量为:

类似的，可求得流向其他可能最先或最严重引起电压态势异常且需重点监控的非待控节点（设为k）的无功增量ΔQi，k:

式中:αi，k为补偿站i对节点k实施无功增援调控时，能够量化无功补偿增量泄流程度的泄流比，主要用于考察可能发生的节点k电压越限问题。

αi，j和αi，k虽 然 数 学 意 义 相 同，但 二 者 的 物 理 意义不同:在增援调控过程中，前者用于考察站点i对待控节点j的泄流效应问题，而后者用于监视可能出现的非待控节点电压态势异常问题。在下文具体讨论的优选参与待控风电场PCC 电压增援调控任务的候选无功补偿站的应用中，可选择αi，j较小且αi，k较大的邻近站点i承担或分担增援调控量。

2 风电场PCC 电压系统侧增援调控站的优选方法

2.1 邻近补偿站参与增援调控的基本条件

设在一定的运行工况下，某邻近补偿站i增发无功补偿功率ΔQi后，会不同程度地引起节点i、待控风电场并网节点j和周边其他需重点监控的非待控节点k的电压幅值各自变化ΔVi、ΔVpcc，j和ΔVk，由此定义节点i的电压-无功调节自灵敏度系数［26］（自调压增益）、节点i对j的和节点i对k的电压-无功调节互灵敏度系数（互调压增益）分别为:

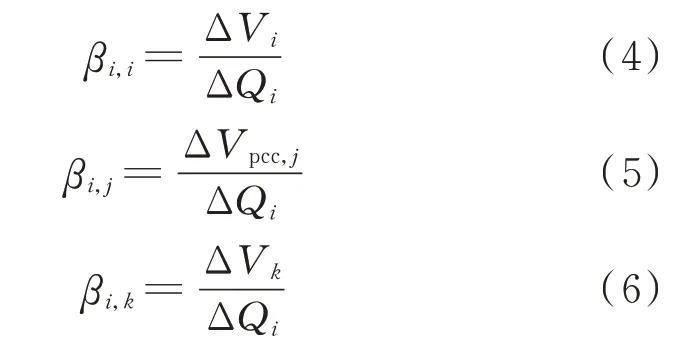
因为邻近无功补偿站i在增发无功补偿功率对待控风电场并网节点j提供调压能力增补时，前提条件是必须保证增补过程不能导致节点i和k的电压越限，故需要对式（7）中的补偿结果进行修正和限制。

考虑节点i和k的电压约束，补偿站i增发无功补偿功率ΔQi必须满足如下关系:

式中:Vi，max和Vi，min分别为节点i电压上、下限；Vk，max和Vk，min分别为节点k电压上、下限。

基于式（8）可推得对应的ΔQi允许范围如下:

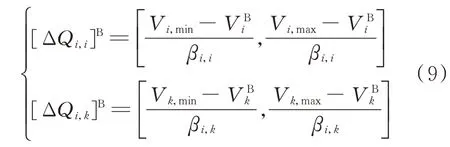
式 中:ΔQi，i和ΔQi，k分 别 为ΔQi中 实 际 对 节 点i和 节点k起到无功补偿作用的部分；[·]B表示在实施某次无功增援调控时物理量的允许取值范围。

记二者交集为:

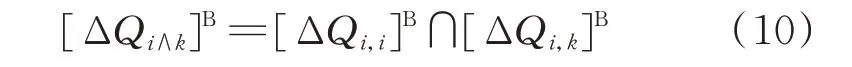
再追加无功补偿站i剩余的无功补偿容量裕度为:

于是，邻近补偿站i能否参与对待控风电场并网节点j增援调控的条件，若满足基本条件则可行的无功补偿功率增发空间应如何取值的判据如下。

1）当[ΔQi]B=∅时，禁止邻近补偿站i参与对待控风电场并网节点j的增援调控。

上述针对待控风电场并网节点j电压异常后，邻近无功补偿站i能否参与增援调控的问题，给出了判断的基本条件及参与增援调控时的可行空间取值判据。由此给出的ΔQdai，虽然某种程度上从供求两方面反映了风电场电压增援调控的综合需求，但本节内容目前仅仅讨论了单个无功补偿站i参与增援调控的问题。就实际工程来看，若单个无功补偿站i参与增援调控可以满足风电场并网节点j电压异常时的无功补偿需求，则无须制定更为复杂的增援调控策略；若不存在可以独立满足无功补偿需求的单个无功补偿站，则需考虑调控多个邻近无功补偿站协同参与增援补偿；若可以满足无功补偿需求的候选无功补偿站不止一个，则存在参与补偿优先级的问题。对后2 种情况，需要继续探讨候选无功补偿站参与增援调控时的排序与优选问题。此时，需要综合考虑多个候选无功补偿站增发无功补偿功率时的泄流效应。

2.2 考虑泄流效应的候选无功补偿站优选方法

2.2.1 主要优选指标

1）指标1:泄流比α

由第1 章分析可知:可选择αi，j较小且αi，k较大的邻近无功补偿站i独自承担或参与分担增援调控量。因此，具体筛选时采用的泄流比指标应同时包括αi，j和αi，k，且当泄流比不符合上述要求时，可将相应无功补偿站从候选集合中去除。

2）指标2:满足基本条件后的供给保障度指标ηi

设由参与待控风电场并网节点j电压异常增援调控的候选无功补偿站组成的集合为Ωj，其中的第i个候选补偿站独立承担增援调控任务时的无功可行增发空间为ΔQdai（可由2.1 节中的模型和方法计算得到），其对独立承担增援调控任务的无功需求ΔQdemi的供给保障度指标定义为:

ηi可以作为对参与调控无功补偿站优先级进行排序的指标之一，它衡量了在考虑无功裕度和电压约束条件下单个补偿站i参与PCC 节点j（PCCj）增援调控时，无功补偿站i补偿供给无功功率的能力，即其数值越大，表示无功资源保障能力越强，越有理由被赋予更高的优先级参与对待控风电场并网节点电压异常实施的增援调控任务。

在线应用时，ηi主要依据当前状态或预估状态距 目 标 电 压 值Vobjpcc，j的 偏 差 量ΔVobjpcc，j等 关 键 信 息 进行滚动计算。

3）指标3:满足基本条件后的电压支撑度γi,j

除ηi外，还可继续考虑第i个候选无功补偿站在增发无功补偿功率ΔQi时出现的泄流效应对增援调控的不良影响，并定义新的指标用于对参与调控无功补偿站优先级进行排序。

由式（5）形式可知，互灵敏度系数（互调压增益）βi，j考 察 的 是 无 功 补 偿 站i总 无 功 补 偿 功 率ΔQi与ΔVpcc，j的关系，但严格意义上能够改善电压变化ΔVpcc，j的无功功率只是其中的ΔQi，j部分，其余均可纳入泄流成分考虑。因此，为考察候选无功补偿站i实际无功输出ΔQi中流向待控节点j的量对ΔVpcc，j的调控效果，重新定义如下形式的互灵敏度系数（互调压增益）:

由式（2）可推出:

将式（19）最右端的系数定义为电压支撑度γi，j:

式（20）定义的电压支撑度综合了自调压增益βi，i、零 泄 流 互 调 压 增 益βdrai，j和泄流比αi，j的联合影响或作用，在零泄流互调压增益越大、自调压增益越小、泄流比越小的条件下，γi，j越大说明无功补偿站i对待控风电场并网节点j电压实施增援调控的灵敏性（增益）越高。由式（20）可知，在实际应用过程计算电压支撑度时，可以由互灵敏度系数βi，j和自灵敏度系数βi，i相除直接得到。

另由式（19）物理含义可知:电压支撑度系数反映在候选无功补偿站i电压允许最大上调/下调范围内，待控风电场并网节点j电压能够最大上调/下调改善的程度。对γi，j越大的候选站i，其被选为参与调控站的优先级应越高。

2.2.2 优选方法

对参与增援调控任务的无功补偿站进行优选的过程，主要分为初选和排序2 个阶段。

2.2.2.1 初选

初选的主要目的是确定Ωj的具体组成。一般的，初选只需秉承“不求选准、但求选对”的原则，即对候选集合Ωj中的任一无功补偿站，哪怕Ωj中只包含该补偿站一个元素，它也应该能够发挥比较正向的增援调控作用。

因此，本文基于补偿站剩余的无功裕度x1=[ΔQBi，sur，min，ΔQBi，sur，max]、补 偿 站 剩 余 的 电 压 调 整 裕 度x2=[ΔVdni，max，ΔVupi，max]、与 补偿站有 线路直接 相 连的邻近其他节点电压到限或近限程度x3、与待控风电场并网点间的电气距离［27］x4等信息，确定候选变电站集合Ωj。具体地，可将待控风电场周边具有较大x1、x2、x3和较小x4的无功补偿站纳入考虑范围。

在得到候选集合Ωj后，可以基于第1 章“选择αi，j较小且αi，k较大的邻近站点i承担或分担增援调控量”，将不符合此要求的无功补偿站从集合Ωj中剔除，以适当控制实际应用过程可能出现的Ωj元素过多的现象。在本文的第4 章算例中，将αi，j的阈值设定为0.44，即从Ωj中剔除αi，j大于0.44 的补偿站。

2.2.2.2 排序

在组成集合Ωj后，需要对其中的候选无功补偿站进行排序。具体排序可以基于不同的调控目标进行。

1）在以无功资源调控代价最小且保证消除ΔVobjpcc，j的前提下，将ΔQdemi较小且ηi最大的列为最高优先级，ΔQdemi较大且ηi最小的列为最低优先级，剩下的补偿站再按规律依次排序。对ΔQdemi较大且ηi很低的候选补偿站，可禁止其参与补偿。在本文的第4 章算例中，将ηi的阈值设定为30%，即从Ωj中剔除ηi低于30%的补偿站。

2）在追求电压支撑灵敏性、兼顾上调/下调鲁棒性（考虑风电场出力不确定性导致PCC 电压频繁在上调和下调间切换的需要）的前提下，将γi，j最大者列为最高优先级，次大者列为次优先级，其余依次类推。对γi，j数值非常小者，可列为禁止参与调控站。在本文的第4 章算例中，将γi，j的阈值设定为0.4，即从Ωj中剔除γi，j低于0.4 的补偿站。

最后，综合1）和2）的排序结果，将二者均排序靠前的候选无功补偿站置于较高优先级，将二者均排序靠后的候选无功补偿站置于较低优先级，若不存在二者均排序靠前或靠后的候选无功补偿站，则只需将其排在中等优先级（处于较高优先级和较低优先级之间），纳入候选集。然后基于下文所述的2 种决策方法，分别计算每个补偿站的无功补偿增量。

3 系统侧增援调控站无功补偿增量的决策方法

设在对集合Ωj进行排序和末位淘汰后，得到新的集合并将其命名为Ωj，new。对新集合，终选过程的主要任务是决策各补偿站具体增发/少发多大的无功功率ΔQi。对此问题，本文设计了如下2 种决策方法。

3.1 基于综合排序结果的启发式决策方法

由2.2.2 节综合排序方式可知，高优先级的无功补偿站具有更小的无功需求ΔQdemi、更高的需求保障度ηi和更高的电压支撑度γi，j，它们理应更多地承担增援调控任务。

基于上述分析，定义分配总增援无功调控量ΔQT的综合权重系数ωi如下:

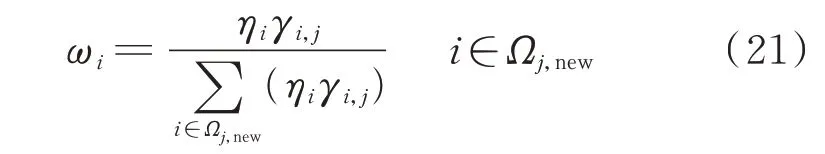
式（21）定义的综合权重系数ωi综合考虑了无功保障度ηi和电压支撑度γi，j的影响，评估了参与电压增援调控的补偿站的重要程度，即综合权重系数越大，补偿站补偿效果越好，因此补偿站应分摊到的无功补偿量就越多。

依上述权重系数ωi分配ΔQT后应使待控风电场并网节点j的电压偏差ΔVobjpcc，j得以消除，即应满足如下等式关系:

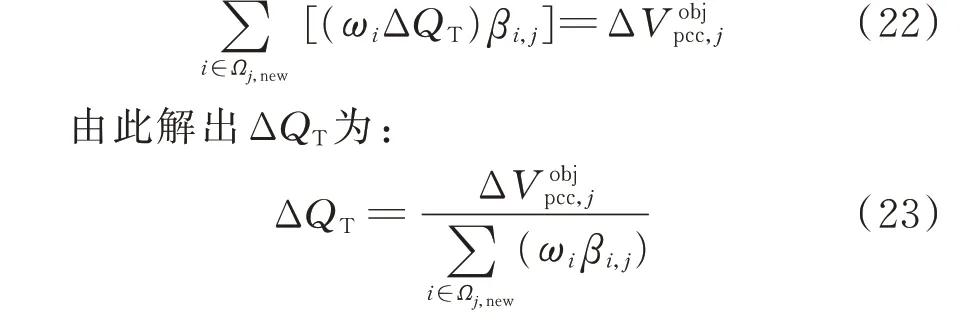
于是可得决策结果为:

3.2 基于线性规划模型的优化决策方法

ΔQi的决策问题还可由如下线性规划模型［28］加以解决。

1）目标函数

式中:ci为无功补偿站i的控制代价，单位元/Mvar。

2）约束条件

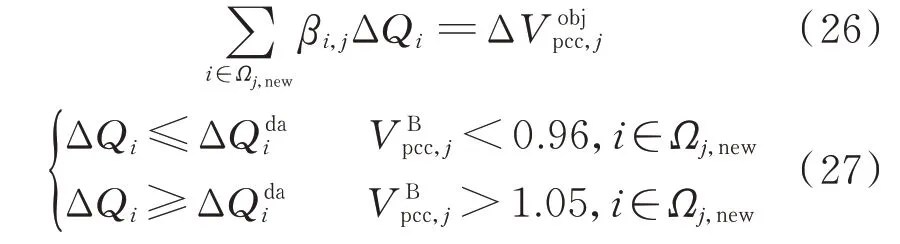
式（25）目标函数追求控制代价最小化。当将Ωj，new中所有参与调控无功补偿站的ci均设为相等时，控制代价最小化将等价于控制总量最小化。

式（26）为待控风电场并网节点j的电压偏差均由参与调控无功补偿站通过增援调控方式改善时的等式约束；式（27）为反映各参与调控无功补偿站增发/少发的无功功率不超过由其独立承担增援调控任务时的量的不等式约束。由于ΔQdai已经考虑了电压Vi和Vk的限值要求，在满足约束式（27）的条件下，节点i和k的电压幅值会自动处于对应的上、下限范围内，故约束条件中不再显性包含该不等式约束。

由于本节中搭建的是低维线性规划模型，故很容易快速求解出ΔQi（i∈Ωj，new）。

3.3 决策方法的算法步骤与实现流程

图2 所示为系统侧对某风电场并网节点电压实施增援调控时的具体决策过程。

图2 增援调控决策流程图Fig.2 Decision-making flow chart of reinforcing dispatch and control

该流程适用于如下2 种模式:对短期预防性决策模式，即基于短期发电及负荷预测数据，进行潮流计算预估相应预防性决策时窗内的电压走势；对超短期预防性决策模式，即基于超短期内风电出力波动的预测数据，能量管理系统进行潮流计算预估相应预防性决策时窗内的电压走势。对于其中任意一种决策模式，若并网节点j电压正常，则决策模块一直处于待命状态；若风电场并网节点j的电压越限，则继续以下步骤。

步骤1:判断风电场j是否发出增援调控请求，若没有则该模块处于待命状态，若发出请求则执行步骤2。

步骤2:计算ΔVobjpcc，j=Vobjpcc，j-VBpcc，j。

步骤3:基于2.2.2 节对系统侧参与调控无功补偿站进行优选。

步骤4:基于3.1 节或3.2 节中提出的方法，分别计算参与调控补偿站的决策量。

步骤5:对计算结果进行潮流校核，通过后将无功补偿增量任务分摊给有关补偿站执行。

步骤6:判断风电场并网节点j是否发出新的请求，若发出请求则会发出新一轮增援调控请求信号，若未发出请求则模块重新进入待命状态。

步骤7:判断参与调控补偿站的无功裕度是否充足，若余量为0 则执行步骤8，若有余量则返回步骤2。

步骤8:实施辅助调压措施，调节该风电场或其他风电场的无功出力，或请求其他常规电源参与增援调控。

步骤9:并网节点j电压恢复至系统规定的范围内则调压结束。

4 算例分析

4.1 基础数据

算例系统在IEEE 39 节点系统基础上进行部分改动后获得（见图3），基准电压为345 kV，基准功率为100 MVA。要求增援调控策略实施后，并网点电压恢复至0.97～1.05（标幺值）。具体改动包括:①在节点16（PCC）处接入1 个等效电源，同时取消该节点原先的负荷，该等效电源为计及风电场内机组输出、场内无功源输出、场内线路损耗以及场用电（含就地负荷）形成的等效模型；②设参与风电场并网节点电压增援调控的候选无功补偿站为邻近的节点15、17、19、21 和24，每个补偿站内无功补偿设备不限于静止无功补偿器（SVC）、电容器组、调相机，且后文计算出的补偿站决策解为该节点无功源的总无功输出。

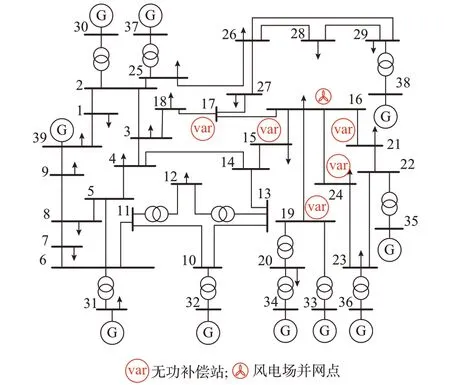
图3 改进的IEEE 39 节点系统Fig.3 Modified IEEE 39-bus system

4.2 模拟工况

在4.1 节给出的系统模型数据基础上，模拟4 种系统运行工况。负荷总有功和无功消耗与风电场等效有功和无功输出见表1，每个节点的有功和无功负荷具体见附录A 表A1 至表A4。

表1 4 种模拟工况下的系统状态信息Table 1 System state information under four simulated conditions

在表1 的4 种模拟运行工况下，候选无功补偿站所在节点15、17、19、21 和24 及其周边部分节点的电压水平列于表2。表中同时给出了节点的电压限值。

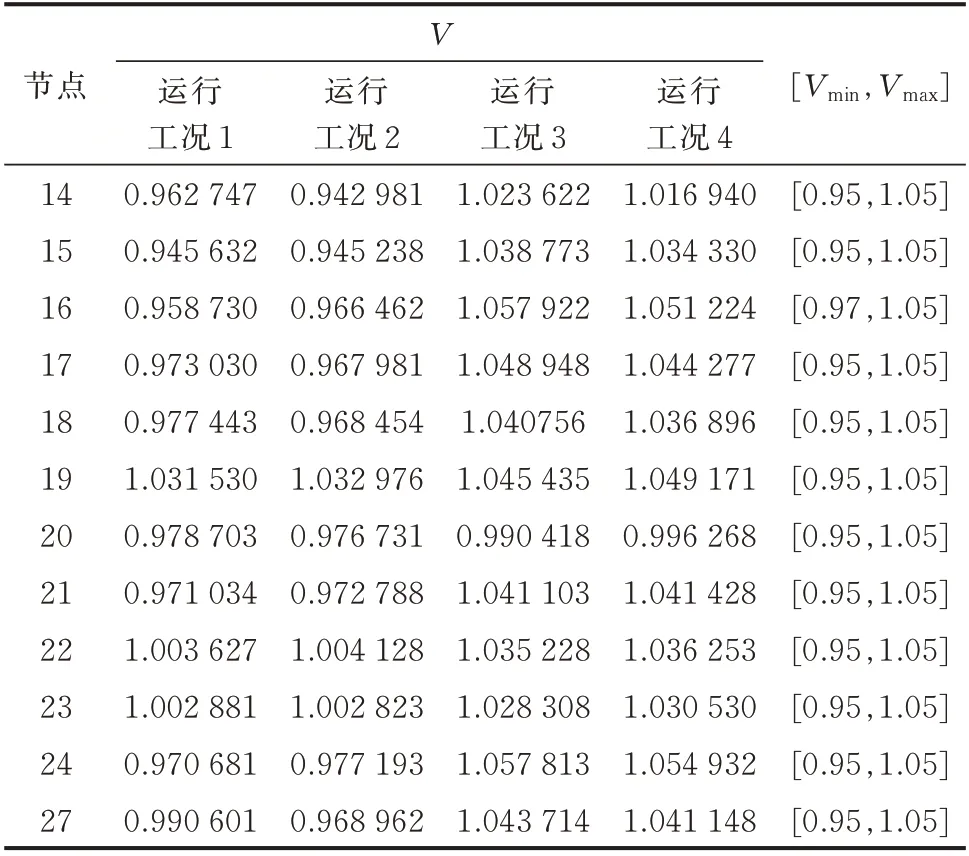
表2 4 种模拟工况下的部分节点电压Table 2 Voltage of partial nodes under four simulated conditions

4.3 增援调控决策过程计算结果

由表2 可知，4 种运行工况下的风电场PCC 电压均不在电压规定范围内。此时，若希望通过网侧无功补偿站的增援调控辅助风电场PCC 电压能够恢复至0.99（标幺值），则需要从候选的5 个站点中进行优选决策。为验证本文创新点，针对所提出的2 种方法，基于附录B 中阐述的2 种方法（方法3 和4）设置了2 组对比算例。

4.3.1 候选站优选指标计算结果

1）泄流比指标α与电压-无功调节自（互）灵敏度系数β计算结果

在模拟工况下，令5 个补偿站增发的无功功率为0.01（标幺值），基于式（1）与无功增发前后的系统潮流结果，计算出5 个候选无功补偿站的泄流比指标，具体结果见附录A 表A5。由表A5 可见，在运行工况1 下，以候选补偿站15 为例，若令该站增发无功功率，则只有67.17%流向风电场（节点16），剩余的32.83%流向了周边的节点14。若只考虑运行工况1 下的5 个补偿站的泄流比结果，选择调控候选站24 增补无功功率，相对于其他候选站效果更佳。

在模拟工况下，令每个补偿站增发0.01（标幺值）的无功功率，基于式（4）至式（6）、式（14）与无功增发前后的系统潮流结果，计算出5 个候选无功补偿站的电压-无功自（互）灵敏度系数指标，计算结果见附录A 表A6。

2）供给保障度指标η计算结果

由式（7）可求出某无功补偿站单独承担增援调控任务时的无功增发量ΔQdemi，以及考虑补偿站剩余的无功容量裕度、补偿站和周边变电站节点电压限值约束后的可行增发空间ΔQdai，从而利用式（13）求出无功需求保障度指标，指标结果见附录A表A7。

3）电压支撑度指标γ计算结果

由式（20）可求出无功补偿站对风电场并网点电压实施增援调控时的电压支撑度，指标结果见附录A 表A8。

4.3.2 补偿站优选结果

由于本算例需要使风电场PCC 电压调整至电压规定范围内，而风电场周边具有电压调整空间且具有无功增发潜力的邻近变电站只有15、17、19、21和24，故将它们全部纳入初选范畴。于是，接下来分别针对4 种模拟运行工况，对5 个补偿站进行优先级排序。

以模拟运行工况1 为例，由附录A 表A5 泄流比指标排出5 个候选站参与调控优先级由高到低依次为:站24、站15、站17、站21、站19；由表A5 保障度指标排出的优先级为:站15、站21、站24、站17、站19；由表A6 支撑度指标排出的优先级为:站24、站17、站15、站21、站19。依据设定的泄流比、保障度和支撑度的阈值，剔除不满足条件的无功补偿站，即确定模拟运行工况1 中最终参与增援调控的补偿站为站15 和站24。并依据以上方法，形成每一个模拟运行工况下的补偿站候选集合Ωj，new。

4.3.3 补偿站增援调控量决策结果

1）基于综合排序结果的启发式决策方法的决策解

根据保障度ηi和电压支撑度γi，j，分别计算得出4 种运行工况下补偿站的综合权重系数ωi列于附录A 表A9。另外，不考虑泄流效应的影响，只考虑电压灵敏度定义的ω′i的计算结果也列于表A9。依照前文所述，综合表A9 中ωi的计算结果和补偿站候选集合Ωj，new计算出4 种运行工况下的补偿站决策解（启发式解1、2、3、4），以及不考虑泄流效应的补偿站决策解（灵敏度解1′、2′、3′、4′）如图A1 所示，每个补偿站决策量数值见表A10。

由附录A 图A1 可知，相比于只考虑补偿站的电压灵敏度，基于综合排序结果的启发式决策方法计算出的补偿站总决策量较小，参与增援调控的补偿站数目较少，若每个补偿站调节成本一致，则基于启发式决策方法的补偿站调节总成本低于只考虑补偿站电压灵敏度的决策方法的补偿站调节总成本。

将启发式决策解和灵敏度解分别代入潮流程序进行检验，可得施加增援调控后4 种模拟运行工况下的系统状态，如附录A 表A11 所示。可见，仅从技术特性而言，2 种决策结果中风电场PCC 电压均与设定的目标值0.99（标幺值）非常接近（最大相对误差发生在启发式解4 中，为0.515 1%），符合工程应用要求。另外，在补偿站实施增援调控的过程中，其周边非待控节点的电压也未发生越限的情况。

2）基于线性规划模型的优化决策方法的决策解

假设5 个补偿站调控成本相同，则控制代价最小化将等价于所有补偿站无功增量绝对值的总量最小化。基于线性规划模型计算补偿站候选集合Ωj，new中4 种运行工况下补偿站决策解（线性规划解1、2、3、4），以及不考虑泄流效应的补偿站决策解（线性规划解1′、2′、3′、4′）如附录A 图A2 所示，每个补偿站决策量数值见表A10。

将附录A 图A2 中2 种线性规划模型的决策结果代入潮流程序进行检验，可得施加增援调控的系统状态，如表A12 所示。可见，2 种决策结果对应的风电场PCC 电压均与设定的目标值0.99（标幺值）非常接近（最大相对误差发生在线性规划解4′中，为0.551 0%），符合工程应用要求。另外，针对线性规划解1～4 对应的系统调控效果，未发生非待控节点电压越限的情况。针对线性规划解3′和4′对应的系统调控效果，出现周边邻近节点（节点15）的电压越限情况。

通过调压方法的算例对比，验证了本文所提出方法的有效性。又因为在风电场内部增加无功补偿装置导致产生了额外的设备投入成本及维护成本，本文方法中调节成本的产生来源于主网侧补偿站内富裕无功设备的动作。这类调节成本低于前一种方法中的总经济成本，且在时效性方面能及时解决风电场并网点电压越限的问题，因此本文提出的方案优于在风电场内部增加无功补偿设备的方案。

4.3.4 分析与讨论

本文研究的风电场并网点电压增援调控问题，重点关注的是风电场并网点及其周边节点（即定义的非待控节点）的电压质量问题，属于局部电网（节点）的电压重点调控问题，因此，所建立的求解模型只需为实现局部系统优化的小型模型。

另外，模型中只有节点电压-无功调节灵敏度系数等相关物理量的基础信息，来自常规潮流计算结果，其余无须依赖更为复杂的全网无功调度模型及其优化结果［29-30］。因此，方法既考虑了全网运行条件变化后的关键潮流信息，保障决策结果具有对电网运行方式变化的适应性，又降低了不必要的复杂计算，有利于重点针对风电场PCC 电压调控问题精准施策。

因此，本文在建模复杂度和计算规模均降低的情况下，做到了面向技术指标及面向技术和经济指标综合要求时的高效决策，其电压调控效果经全网潮流计算检验，能够满足风电场并网点电压增援调控决策的需要。

5 结语

本文针对调控系统侧无功资源对风电场并网点电压实施增援的问题，从考虑无功补偿增量泄流现象出发，研究并提出了参与调控补偿站的筛选方法和调控任务分配决策方法。所得结论主要如下。

1）对无功资源缺乏的风电场并网点电压实施系统侧增援调控时，无功泄流比较小的补偿站应优先考虑列入参与调控补偿站集合。

2）在参与调控补偿站满足增援调控基本条件的前提下，无功供给保障度和电压支撑度大者优先考虑参与增援调控并承担较大补偿份额。

3）针对筛选出的参与调控补偿站集合进行增援调控任务分配时，启发式决策方法更侧重于对技术性能的考虑，而线性规划模型决策方法可综合考虑技术、经济两方面性能，是二者决策的结果，只要参与调控补偿站提供的总调控能力足够，均可使并网点电压调整至设定的目标值；结合问题特点采用的线性规划模型具有简便、高效决策的特点，能够适应局部电网并网点电压控制问题的需要。

4）本文方法可推广应用于无功薄弱的负荷或电源（待控）节点周边（中等电气联系紧密度）存在的这样一类补偿站:自身具有富裕无功补偿资源且对待控节点进行增援补偿的无功泄流比较小；当电网局部存在多个待控节点和多个补偿站节点，且相互之间影响关系复杂，或增援调控决策结果受运行方式影响多变时，方法相对于传统大规模无功优化方法的优势将变弱。

本文受到智能电网保护和运行控制国家重点实验室资助的开放课题（新能源高渗透率区域电网多无功源协调控制方法研究，SGNR0000KJJS1907537)的资助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。