多回LCC-HVDC分区馈入电网中柔性直流接入位置的确定方法

曹 昕，韩民晓，邵红博，于琳琳，周光阳

（1. 华北电力大学电气与电子工程学院，北京市102206；2. 国网河南省电力公司电力科学研究院，河南省郑州市450052）

0 引言

大力建设基于电网换相换流器的高压直流（line commutated converter based high voltage DC，LCC-HVDC，以下简称传统直流）输电工程是贯彻“西电东送”和“新基建”国家战略的主要方式之一［1-2］。但随着传统直流建设，中国华东电网和南方电网形成了多回传统直流密集馈入的区域电网［3］。

截至2018 年底，有8 回传统直流馈入华东电网［4］、10 回馈入南方电网［5］。上述2 个电网中，传统直流换流母线之间电气距离较近。交流故障极易引起多个换流站同时发生换相失败，严重时会引起多次换相失败甚至停运。省级电网中，有两回传统直流馈入河南省网，且电气距离较近，引起同时换相失败的交流故障区域范围较大［6］。山东电网也存在两回传统直流分层馈入、电气距离较近的问题［7］，发生同时换相失败的可能性也较大。

扩大交流系统规模是解决上述问题的方法之一。但是，文献［8］指出同步电网的规模受频率稳定、低频振荡频率和同步支持效应的约束，仅扩大交流系统可能会带来其他问题。

南方电网拟采用基于电压源型换流器的高压直流（voltage source converter based high voltage DC，VSC-HVDC，以下简称柔性直流）输电技术使传统直流分区馈入［9］。文献［10］提出将广东电网分区、异步运行、柔性直流连接的方案。文献［11-12］针对广东电网2030 年规划，比较了多种分区方案，认为采用柔性直流分区运行在多馈入有效短路比、交直流相互影响和短路电流抑制方面表现较好。河南电网也开展了采用柔性直流优化运行的研究［13］。

通过柔性直流互联实现电网分区运行是解决多馈入传统直流系统容易发生同时换相失败等问题的较好方案。但是，现有文献针对这种场景下柔性直流接入位置的确定问题研究不足。文献［6］以柔性直流支撑断面的输电能力，分析断面的薄弱点并规划柔性直流。文献［14］通过校验正常和N-1 方式下，分区内线路是否过载等问题，从候选接入位置中选择所需柔性直流容量最小的节点作为接入点。两种方法均以柔性直流改造输电断面线路，没有考虑柔性直流接入更合理的位置。文献［15］针对城市电网分区以柔性直流改造现有交流联络线，提出了评价柔性直流接入位置的指标，但并未考虑传统直流馈入对各分区的影响。

本文采用以柔性直流对多馈入传统直流系统进行分区的方案，针对柔性直流在分区中接入位置的问题提出了评价指标及流程。首先，基于雅可比转移矩阵［16-17］建立了计及传统直流和柔性直流的全系统微增量模型，以计算柔性直流的运行阻抗，并推导出基于阻抗的有效短路比（impedance based effective short circuit ratio，IESCR）［18-20］的计算方法。针对柔性直流接入的系统拓扑，给出了理论计算简化处理方法，得到了柔性直流接入位置、柔性直流传输功率与IESCR 的关系。随后，考虑正常运行状态和N-1 运行状态，提出了包括IESCR 在内的9 个评价指标及其计算方法，给出了评价柔性直流接入位置的评价流程。基于IEEE 39 节点模型给出了算例。对3 个柔性直流接入位置计算出了各评价指标的值，并给出了3 个接入位置的得分，确定了其中的最优接入位置。

1 基于运行阻抗的短路比计算

1.1 系统拓扑

针对多馈入传统直流系统进行电网分区并以柔性直流互联各分区的场景下柔性直流接入位置的问题，可采用如图1 所示的简化拓扑进行理论分析。

图1 考虑柔性直流接入位置的系统拓扑Fig.1 System topology considering accessing locations of VSC-HVDC

图1 中:Pdc、Qdc分别为传统直流注入交流系统的有功、无功功率；Pl、Ql分别为传统直流经无功补偿后注入交流系统的有功、无功功率；P1、Q1和P2、Q2分别为注入和流出母线2 的有功和无功功率；PVSC、QVSC分别为柔性直流注入交流系统的有功、无功功率；接入位置1 表示柔性直流接入传统直流的换流母线处，即母线1 处，对应的电压为U˙1；接入位置2 表示柔性直流接入交流系统中任意节点，即母线2 处，对应的电压为U˙2，该节点至传统直流换流母线和至等效电源母线的阻抗分别用等效阻抗Z1和Z2表示；Zf为无功补偿装置的等效阻抗；Pf和Qf分别为无功补偿装置吸收的有功和无功功率。

1.2 IESCR

IESCR［18-20］可由下式计算:

式中:ul为传统直流换流母线的电压幅值；Zeq为计及柔性直流运行阻抗的系统等效阻抗，可以表示为

对于柔性直流的运行阻抗ZVSC，计算式如下:

式中:Δuvd、Δuvq和Δivd、Δivq分别为柔性直流换流站输出的电压和电流在dq坐标系下的微增量。

1.3 传统直流和柔性直流的微增量模型

下文以下标d、q分别表示对应变量的d轴和q轴分量；“Δ”表示微增量；下标“0”表示对应变量的稳态值。

1）传统直流的微增量模型可以描述为:

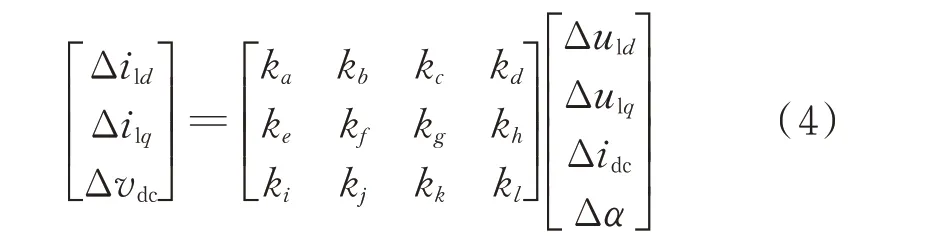
式中:参数ka～kl可由文献［21］提出的方法计算；idc和vdc分别为传统直流的直流电流和电压；il为传统直流注入交流系统的电流；α为触发角。

对于传统直流的逆变侧，其触发角可以描述为:

熄弧角γ和换相角μ的关系可以描述为:

式中:Xc为换相电抗；kT为换流变压器的变比。

当逆变侧采用定熄弧角控制即Δγ=0 时，将式（6）代入式（5），线性化并消去常数项可得:

其中

则式（4）可以简化为:

2）柔性直流的微增量模型

当柔性直流采用PQ控制时，其外环特性可以描述为:

式中:uv和iv分别为柔性直流输出电压和电流。

线性化式（11）并消去常数项可得:

1.4 基于雅可比转移矩阵的全系统微增量建模

由瞬时功率计算式线性化并忽略高次项，得到传统直流和柔性直流的有功、无功功率微增量，如下式:

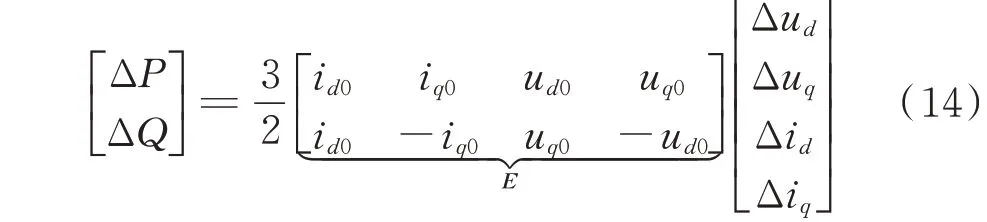
式中:u和i分别为节点电压和注入电流的模值；P、Q分别为注入节点的有功和无功功率。

系统节点电压的微增量模型可以表示为:

式中:θ为采用直角坐标系时节点的电压相角。

建立交流系统的雅可比转移矩阵［16-17］如下:

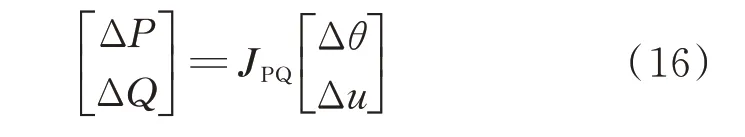
式中:JPQ为雅可比转移矩阵，下文给出计算方法。

交流系统中，任意两节点的计算式可描述为:

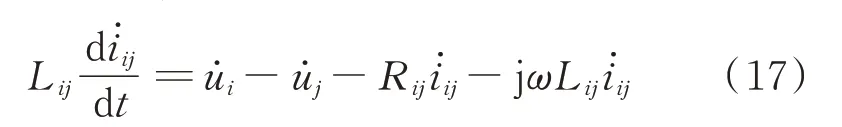
式 中:i˙ij为 流 过 节 点i、j之 间 的 阻 抗Rij+jωLij的 电流，其中Rij、Lij、ωLij分别为节点i、j之间的电阻、电感、电抗；u˙i、u˙j分别为节点i、j的电压。

对式（17）进行dq坐标变换、线性化并忽略高次项可得:

式中:θi和θj分别为节点i和j的电压相角。

联立式（14）、式（15）和式（18）即可得到式（16）中雅可比转移矩阵JPQ的元素。此时，基于雅可比转移矩阵建立起了考虑传统直流和柔性直流的交流系统微增量模型，整个计算流程如图2 所示。进而，可以求出Δuvd、Δuvq、Δivd和Δivq，由式（3）计算出ZVSC，再由式（1）计算出IESCR。

图2 基于雅可比转移矩阵的交流系统微增量模型Fig.2 Small-signal model of AC system based on Jacobian transfer matrix

2 柔性直流接入位置对IESCR 的影响分析

2.1 分析过程简化处理

以图1 所示的区域n+1 为分析对象，设置交流系统的等效阻抗Z1+Z2等于（3.78+j14.10）Ω；传统直流注入交流系统的有功功率为定值，熄弧角γ为17°，换 相 角μ为20°。换 流 母 线 的 电 压U˙1取230∠0° kV。柔性直流换流站采用定有功和定无功功率控制。这种做法简化了计算复杂度，原因如下。

1）通过给定柔性直流接入母线和等效系统母线电压，能够唯一确定系统的潮流分布，省略了迭代过程。同时，设置传统直流的母线电压为额定值，直流电压和直流电流都将保持恒定，即Δidc=0。

2）传统直流整流侧采用定功率控制、逆变侧采用定熄弧角控制，使得馈入交流系统的有功和无功功率恒定，忽略了直流控制对潮流计算结果的影响。

3）柔性直流采用定PQ控制，使得柔性直流注入交流系统的有功和无功功率恒定，即ΔPVSC=0、ΔQVSC=0。忽略了柔性直流注入功率变化对潮流计算和运行阻抗计算的影响。

4）以图1 所示等效系统为分析对象，简化了系统拓扑且降低了计算复杂度。通过分配Z1和Z2模值大小实现了对柔性直流不同接入位置的定性分析。

2.2 接入位置与柔性直流传输功率和IESCR 的关系

设置交流系统的等效电源电压E˙ 为215∠-15°，传统直流馈入交流系统的有功功率分别为1 000 MW 和1 100 MW，计算柔性直流换流站在不同接入位置处的IESCR。传统直流的IESCR、柔性直流注入的有功和无功功率如附录A 图A1所示。

由附录A 图A1（a）可以发现，当传统直流的馈入功率增大时会使IESCR 减小。同时，随着柔性直流接入位置逐渐远离传统直流的换流母线，IESCR呈下降趋势。由附录A 图A1（b）和（c）可以发现，随着柔性直流接入位置逐渐远离传统直流的换流母线，柔性直流注入的有功和无功功率的模值呈逐渐增大的趋势。

表1 和表2 分别给出了当传统直流分别馈入1 000 MW 和1 100 MW 功率时，部分Z1模值下对应的柔性直流注入有功、注入无功、IESCR 和柔性直流的运行阻抗。

表1 Pl为1 000 MW 时不同柔性直流接入位置处系统的部分运行参数Table 1 Partial operation parameters at different VSC-HVDC accessing locations when Pl equals to 1 000 MW

表2 Pl为1 100 MW 时不同柔性直流接入位置处系统的部分运行参数Table 2 Partial operation parameters at different VSC-HVDC accessing locations when Pl equals to 1 100 MW

定义2 个计算式分别如下:

式中:ΔPl为100 MW；ΔFIESCR等于当Pl为1 000 MW时的IESCR 减去Pl为1 100 MW 时的IESCR；ΔPVSC和ΔQVSC分别等于当Pl为1 000 MW 时的有功和无功功率减去Pl为1 100 MW 时的有功和无功功率；ΔS为柔性直流传输功率变化量；τ1和τ2没有实际意义，这里仅起到指代作用。

由式（19）除以式（20）得到了ΔFIESCR和ΔS的比值，其含义为某个柔性直流接入位置处，IESCR 的变化量与柔性直流传输功率变化量的比值。对表1和表2 的数据进行处理得到图3。

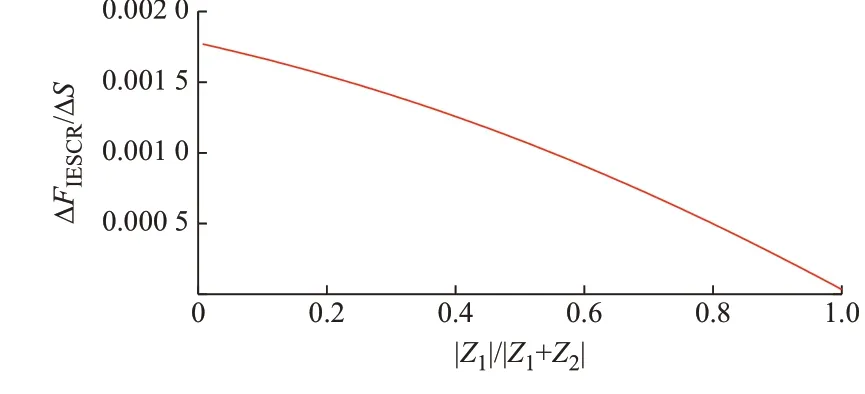
图3 不同接入位置处ΔFIESCR/ΔS 的值Fig.3 Values of ΔFIESCR/ΔS at different accessing locations

综上，随着柔性直流接入位置与传统直流的电气距离减小，柔性直流需要传输的功率有减小的趋势，IESCR 的提高有增大的趋势。

可以发现，仅以传统直流IESCR 的提高来评价柔性直流接入位置是不足的，需要考虑正常运行方式和N-1 运行方式下的其他因素。

3 柔性直流接入位置的确定方法

本章将提出包括IESCR 在内的评价指标及其计算或获取方法，并给出评价流程以确定柔性直流的最优接入位置。

3.1 柔性直流接入位置评价指标

多馈入传统直流系统分区运行并以柔性直流互联所形成的系统，其拓扑结构如图1 中的区域n+1所示。评价柔性直流接入位置需要考虑柔性直流对传统直流、对交流系统和对柔性直流自身的影响。例如，在正常稳定运行时，需要考虑柔性直流接入位置对传统直流IESCR 的提高程度、柔性直流需要传输的功率、分区最大供电能力、变压器负载变化量、各节点短路电流抑制等因素；在N-1 运行状态下，需要考虑柔性直流需要传输的最大功率、引起换相失败的N-1 方式个数、各节点电压变化量、支路潮流变化量等因素。将这些因素设定为评价指标，如表3 所示。

表3 柔性直流接入位置评价指标Table 3 Evaluation indices of VSC-HVDC accessing location

表3 中给出了评价柔性直流接入位置的9 个指标，下文对这些指标进行详细说明并给出计算方法。以下标“q”和“h”分别表示柔性直流接入前后的运行状态，以m表示第m个柔性直流接入位置。

对于短路比变化量F1评价指标，以正常运行状态下柔性直流的最优传输功率为基准，计算柔性直流接入前后IESCR 的差值来衡量，表示为:

式中:FIESCR，q，m和FIESCR，h，m分别为柔性直流接入第m个位置前、后的IESCR 值。

对于变压器负载均匀程度F2评价指标，以正常运行状态下柔性直流的最优传输功率为基准，计算柔性直流接入前后分区内各变压器负载变化的平均值来衡量，表示为:

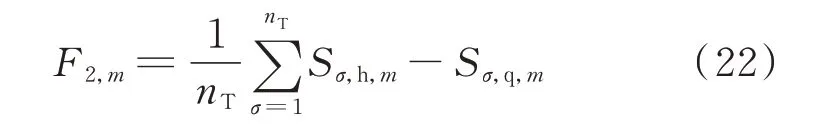
式 中:σ为 变 压 器 编 号；nT为 变 压 器 个 数；Sσ，q，m和Sσ，h，m分别为柔性直流接入第m个位置前、后变压器σ带负载时的视在功率。

对于短路电流水平F3评价指标，以正常运行状态下柔性直流的最优传输功率为基准，计算柔性直流接入前后各节点短路电流变化量的平均值来衡量，表示为:

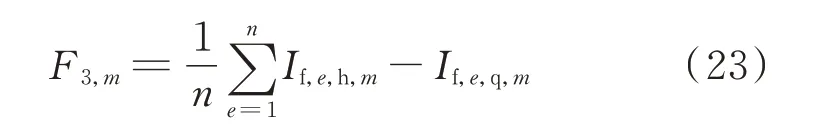
式 中:e为 节 点 编 号；n为 节 点 个 数；If，e，q，m和If，e，h，m分别为柔性直流接入第m个位置前、后节点e的短路电流。

对于最大供电能力F4评价指标，以柔性直流在正常状态下所供电的负载功率为基准，计算柔性直流以最大容量所能供电的最大负载与基准值的变化量来衡量。分别计及有功和无功负荷的变化量，表示为:

式 中:Pld，m，max和Qld，m，max分 别 为 柔 性 直 流 接 入 第m个位置并以最大传输功率运行时，最大供电负荷的有功和无功功率；Pld和Qld分别为正常运行时的负荷有功和无功功率。

需要指出的是，计算该指标时需要柔性直流以最大容量运行且不考虑支路开断，获取最大供电负荷。柔性直流的最大容量是由N-1 方式下柔性直流的最大传输功率计算出视在功率并向上取整获得的。

对于柔性直流传输功率F5评价指标，以正常运行状态下柔性直流最优传输功率的模值来衡量，表示为:

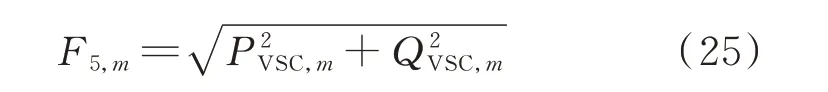
式中:PVSC，m和QVSC，m分别为正常运行方式下柔性直流接入第m个位置后传输的最优有功和无功功率。

对于N-1 运行状态的评价指标，首先需要在各种N-1 方式下对系统进行最优潮流计算，获取柔性直流需要传输的最大功率，再计算F7、F8和F9评价指标。以下标“N-1”表示N-1 运行方式。

柔性直流的最大传输功率可以用来确定柔性直流的容量。评价指标F9以柔性直流的最大传输功率和正常状态下的传输功率的比值来衡量，表示为:

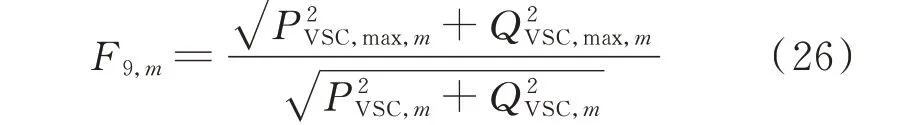
式 中:PVSC，max，m和QVSC，max，m分 别 为N-1 方 式 下 柔 性直流接入第m个位置后传输的最大有功和无功功率。

对于节点电压变化量F7评价指标，以正常运行状态下，柔性直流以最优传输功率接入后各节点电压幅值为基准，计算N-1 运行方式下各节点电压幅值变化量的绝对值再取平均来衡量，表示为:

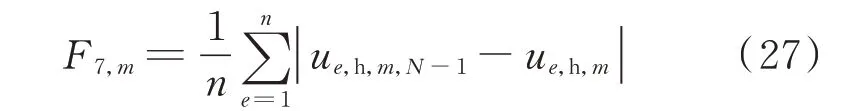
式中:ue，h，m，N-1为当柔性直流接入第m个位置后，在N-1 方 式 下 节 点e的 电 压 幅 值；ue，h，m为 当 柔 性 直 流接入第m个位置后，在正常运行方式下节点e的电压幅值。

对于支路潮流变化量F8评价指标，以正常运行状态下，柔性直流以最优传输功率接入后各支路潮流为基准，计算N-1 运行方式下各支路潮流的变化量的平均值来衡量。分别计及有功和无功功率的变化量，表示为:

式中:ρ表示第ρ条支路；nb为支路总数；Pρ，h，m，N-1和Qρ，h，m，N-1分别为当柔性直流接入第m个位置后，第ρ条支路在N-1 方式下，支路首端流出的有功和无功 功 率；Pρ，h，m和Qρ，h，m分 别 为 当 柔 性 直 流 接 入 第m个位置后，第ρ条支路在正常运行方式下，支路首端流出的有功和无功功率。

需要指出的是，根据N-1 方式的不同，F7和F8会有多组数据。本文通过对各种N-1 方式下获得的F7和F8数据取平均值以确定评价指标最终的值。

传统直流的换相失败发生次数需要借助PSDBPA 软件进行N-1 扫描获得。换相失败发生次数F6评价指标通过统计能够引起传统直流换相失败的N-1 方式个数与潮流能够收敛的N-1 方式个数之比来衡量。

3.2 评价模型搭建及计算流程

3.1 节给出了9 个评价指标，通过不断调整柔性直流接入位置计算和获取各个指标的值，直至遍历所有接入位置，随后代入评价模型计算最后得分。

柔性直流的接入位置对传统直流的IESCR 提高越大、最大供电能力的提高越大，则柔性直流的接入位置越好，而对于其他指标则是越小越好。因此，首先对指标F1和F4取倒数。随后，通过线性归一化函数对各个指标进行处理，即式（29），将数据映射到（0，1）区间。

式中:x代表各个评价指标数据，即F1，m～F9，m；xmax和xmin分别为x中的最大和最小值；y代表归一化后的各个指标数据，以F′1，m～F′9，m表示。

随后，建立线性加权评价模型，表示为:

式中:gm为柔性直流接入第m个位置时由评价模型得到的分数；kλ为第λ个指标的权重。

评价柔性直流接入位置的具体流程如下。

步骤1:计算柔性直流不接入时系统的最优潮流分布，计算传统直流的IESCR 并记录系统潮流分布、节点电压和节点短路电流等信息。

步骤2:给定一处柔性直流接入位置m。

步骤3:计算柔性直流接入后系统的最优潮流，记录柔性直流在正常运行状态下的传输功率、系统的潮流分布、节点电压和短路电流等信息，并计算出此时传统直流的IESCR。进而由式（21）、式（22）、式（23）和式（25）分 别计算评价 指 标F1，m、F2，m、F3，m和F5，m。

步骤4:对柔性直流接入位置m时进行N-1 扫描。轮流开断各个支路，计算系统的最优潮流分布，获取柔性直流的最大传输功率，记录各个N-1 运行状态下的潮流分布、节点电压、引起传统直流换相失败次数以及潮流不收敛次数等信息。进而由式（26）、式（27）和 式（28）分 别 计 算 评 价 指 标F7，m、F8，m、F9，m。随后，还需对各个N-1 运行状态下得到的F7，m和F8，m取平均值。同时，在PSD-BPA 软件中进行N-1 扫描，由引起传统直流换相失败的N-1方式个数与潮流能够收敛的N-1 方式个数之比获得评价指标F6，m。

步骤5:设置柔性直流的容量为最大传输功率时的视在功率并向上取整，在正常运行方式下不断提高负荷，直至达到系统的运行约束，记录此时的最大负荷值。随后，由式（24）计算评价指标F4，m。

步骤6:首先判断是否遍历完毕所有柔性直流可以接入的节点。若已完成则进行步骤7；若未完成，则返回步骤3。

步骤7:对F1，m和F4，m取倒数，由式（29）对各个数据进行归一化处理，再由式（30）计算评价得分。得分最小的结果即为柔性直流的最优接入位置。

整个评价流程如附录A 图A2 所示。

4 算例分析

第3 章对短路比变化量（F1）和柔性直流传输功率（F5）评价指标进行了理论分析。但是这两个指标没有充分考虑N-1 情况下柔性直流接入位置对系统的影响。本章将通过算例对评价指标进行分析，并结合评价流程给出最终的评分。

基于IEEE 39 节点模型，在PSD-BPA 仿真软件中搭建仿真模型；根据CIGRE Benchmark 传统直流模型，将38 节点连接的发电机改为传统直流，额定运行状态下向交流系统提供1 000 MW 和40 Mvar的功率；考虑柔性直流分别接入节点29、16 和6，对应着柔性直流与传统直流的电气距离由小到大；柔性直流采用定PQ控制；取节点32 为平衡节点。拓扑结构如图4 所示。

图4 基于IEEE 39 节点模型的算例拓扑Fig.4 Example topology based on IEEE 39-bus model

设置最优潮流计算的目标函数为运行成本最低，并设置各机组的发电成本相同，柔性直流传输功率的成本为机组发电成本的3 倍。对于实际系统可设置其他目标函数。

按照附录A 图A2 给出的评价流程，首先，分别计算柔性直流不接入、柔性直流接入节点29、柔性直流接入节点16 和柔性直流接入节点6，这4 种情况下系统的最优潮流。记录数据:柔性直流需要传输的功率、传统直流的IESCR、分别由式（21）和式（25）计算出的评价指标F1和F5，如表4 所示。

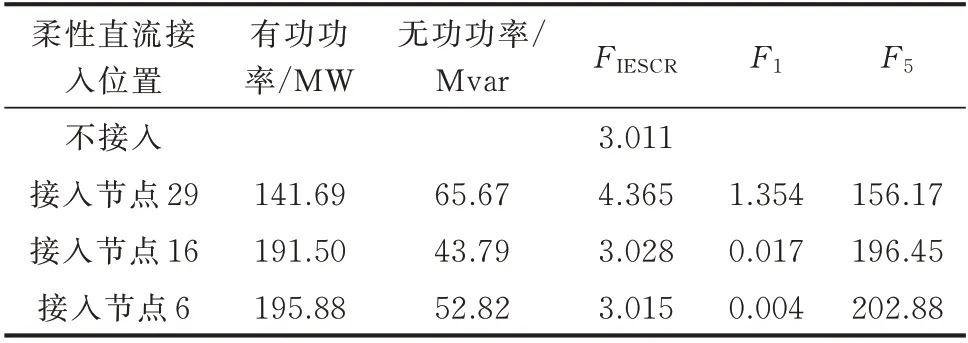
表4 正常运行时的数据和部分评价指标结果Table 4 Data and results of some evaluation indices during normal operation

由表4 可以发现，随着柔性直流与传统直流的电气距离逐渐增大，柔性直流需要传输的功率也逐渐增大，传统直流的IESCR 逐渐减小。这与上一章理论分析的结果相同。

同时，记录这4 种情况下变压器负载和各节点短路电流，由式（22）和式（23）分别计算出评价指标F2和F3。随后，对这4 种情况下的系统进行N-1 扫描，计算N-1 方式下系统的最优潮流。其中，柔性直流需要传输的功率如附录A 表A1 所示。统计柔性直流在N-1 方式下需要传输的最大功率、引起换相失败的次数以获取指标F6，并由式（26）计算指标F9，结果如附录A 表A2 所示。

由柔性直流在N-1 方式下的最大传输功率计算出视在功率并向上取整，记为柔性直流的容量。以此容量作为柔性直流的功率输出限值，在PSDBPA 软件中不断调整负荷的大小，直至系统不满足约束条件，记录此时的负荷大小即为最大负荷，再由式（24）计算出指标F4。在N-1 扫描的过程中，记录各种N-1 方式下的节点电压幅值和支路潮流，由式（27）和式（28）分别计算指标F7和F8，并对各个N-1 状态下计算出的数据取平均值，数据如附录A表A2 所示。

需要指出的是，在N-1 运行方式下，柔性直流接入节点29 会有10 次潮流不能收敛的情况，对应着开断支路两端的节点编号为2-30、6-31、9-39、10-32、16-19、17-18、19-20、26-29、28-29、29-38；没有能够引起换相失败的N-1 状态；其F6为0。柔性直流接入节点16 会有7 次潮流不能收敛的情况，对应着开断支路两端的节点编号为2-30、10-32、19-20、26-28、26-29、28-29、29-38；另外2-3 和25-26 断开会引起换相失败；其F6为0.051 3。柔性直流接入节点6会有8 次潮流不能收敛的情况，对应着开断支路两端的节点编号为2-30、10-32、19-20、25-26、26-28、26-29、28-29、29-38；另外2-3 断开会引起换相失败；其F6为0.026 3。

由表4 和附录A 表A2 可以发现，柔性直流接入位置越靠近传统直流（节点29），其正常运行状态下的评价指标结果越好，例如:短路比提高越大、传输功率越小、变压器负载越均衡、最大供电能力更强，并且换相失败次数为0。但是，其他N-1 运行状态评价指标均是最差的，且柔性直流容量利用率最低。接入节点6，即柔性直流接入点距离传统直流有一定距离，其指标结果与节点29 的结果正好相反，即正常运行状态下的评价指标较差，N-1 运行状态下的评价指标最好；节点16 的指标介于两者之间。

按照评价流程，对F1，m和F4，m取倒数，然后对所有指标进行归一化，数据处理结果如附录A 表A3所示。

假设所有指标权重均为0.111 1，则计算得分为:柔性直流接入节点29 为0.333 3；柔性直流接入节点16 为0.446 3；柔性直流接入节点6 为0.612 5。按照得分最小的方案为柔性直流的最优落点，柔性直流接入节点29 为本文提出的评价流程的最优落点。

对于实际系统，若关注于正常状态下的柔性直流运行，可增大正常状态下评价指标的权重；若系统发生故障的概率较大，则需要多关注N-1 运行状态，即可增大N-1 状态下评价指标的权重。

5 结语

针对多馈入传统直流系统密集馈入同一交流系统所产生的问题，本文研究了对交流电网进行分区，实现各分区间异步运行并以柔性直流互联各分区的方案。针对柔性直流在分区中接入位置的问题，首先，建立了传统直流和柔性直流的微增量模型，基于雅可比转移矩阵搭建了全系统的微增量模型，以计算柔性直流的运行阻抗进而计算IESCR。分析了柔性直流接入位置对柔性直流传输功率和IESCR的影响，并指出仅以IESCR 评价柔性直流接入位置并不充分。

因此，给出了IESCR 增加量、变压器负载均衡程度、短路电流水平、最大供电能力、柔性直流正常传输功率、引起传统直流换相失败次数、节点电压变化量、支路潮流变化量和柔性直流最大传输功率与正常传输功率比值共9 个评价指标，给出了评价指标计算和获取方法，以及柔性直流接入位置的评价流程。

基于IEEE 39 节点模型，给出了算例分析。对柔性直流的3 个接入位置计算了各指标的值，对应着柔性直流的接入位置与传统直流的电气距离由小到大。通过算例分析发现，柔性直流接入位置距离传统直流电气距离较小时，正常运行下的指标表现较好，多个N-1 运行状态下的指标表现较差。其指标的计算结果与距离传统直流较远的接入位置的结果基本相反。

通过本文设置的指标权重计算得分后，节点29为3 个接入位置中柔性直流的最优接入位置。对于实际系统，可以根据实际需求调整指标权重，以获取最优的柔性直流接入位置。

特别指出的是，广义短路比（generalized short circuit ratio，GSCR）［22-24］基于交流系统的扩展雅可比矩阵的最小特征根，定义传统直流的短路比。考虑到GSCR 的建立过程与本文提出的基于雅可比转移矩阵法建立全系统微增量模型的过程相似，采用GSCR 可以省略计算柔性直流运行阻抗的过程，进一步减少计算量。将以GSCR、传统直流的不同控制方式、柔性直流的不同控制方式作为下一步的研究内容。

此外，本文中的电网分区是指分区之间没有交流连接，这种分区方式对多回传统直流同时换相失败的抑制效果较好，而对于实际交流系统，这种场景较为理想。因此，后续将进一步研究交流联络线和柔性直流并列运行的场景中，柔性直流的接入位置确定方法。

本文在撰写过程中得到了瑞典ABB 合作研发中心、瑞典皇家理工学院兼职教师Lennart Harnefors 教授和瑞典皇家理工学院Han-Peter Nee 教授的帮助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。