基于HGDOB与RBFNN的回转支承试验台液压加载控制方法*
□ 都璐远 □ 陈 捷 □ 杨贵超
南京工业大学 机械与动力工程学院 南京 211800
1 研究背景
大型回转支承应用于大型机械中,是机械传动系统中的重要组成部分,其性能优劣直接决定大型机械能否正常作业。通过回转支承试验台可以检测回转支承的质量是否满足出厂要求,为回转支承综合性能的评价提供准确、可靠的试验数据,并为产品设计和改进提供参考[1]。
回转支承试验台以盾构机主轴承和风力发电机回转支承为试验对象,通过监测轴承内外圈位移、振动等信号,检验轴承的运行性能及疲劳寿命。在对回转轴承进行试验时,需要由回转支承试验台对回转轴承进行加载以模拟实际工况,不同的工况及试验对象对应不同的载荷谱。回转支承试验台以液压为动力源,通过油缸拉压顶盖对一对受试回转轴承进行加载,通过控制油缸内的压力来达到对回转轴承进行加载试验的目的。
目前国内的回转支承试验台在加载力控制精度、跟踪性能及响应速度方面还有待提高,在加载时会出现加载命令响应慢现象,控制精度也有10%的误差。笔者针对目前回转支承试验台的不足,设计了一种基于高增益扰动观测器和径向基神经网络的自适应控制算法[2-3],可以有效解决回转支承试验台加载控制精度低、响应慢的问题,对于实际运行中遇到的扰动有一定鲁棒性,具有较高的实用价值。
2 数学模型
回转支承试验台加载油缸如图1所示。回转支承试验台由两个相同的单出杆油缸进行加载[4],并且两个油缸独立加载,笔者针对其中一个加载油缸进行建模,如图2所示。加载顶盖为一整体铸件,对于受力顶盖以弹簧来代替。
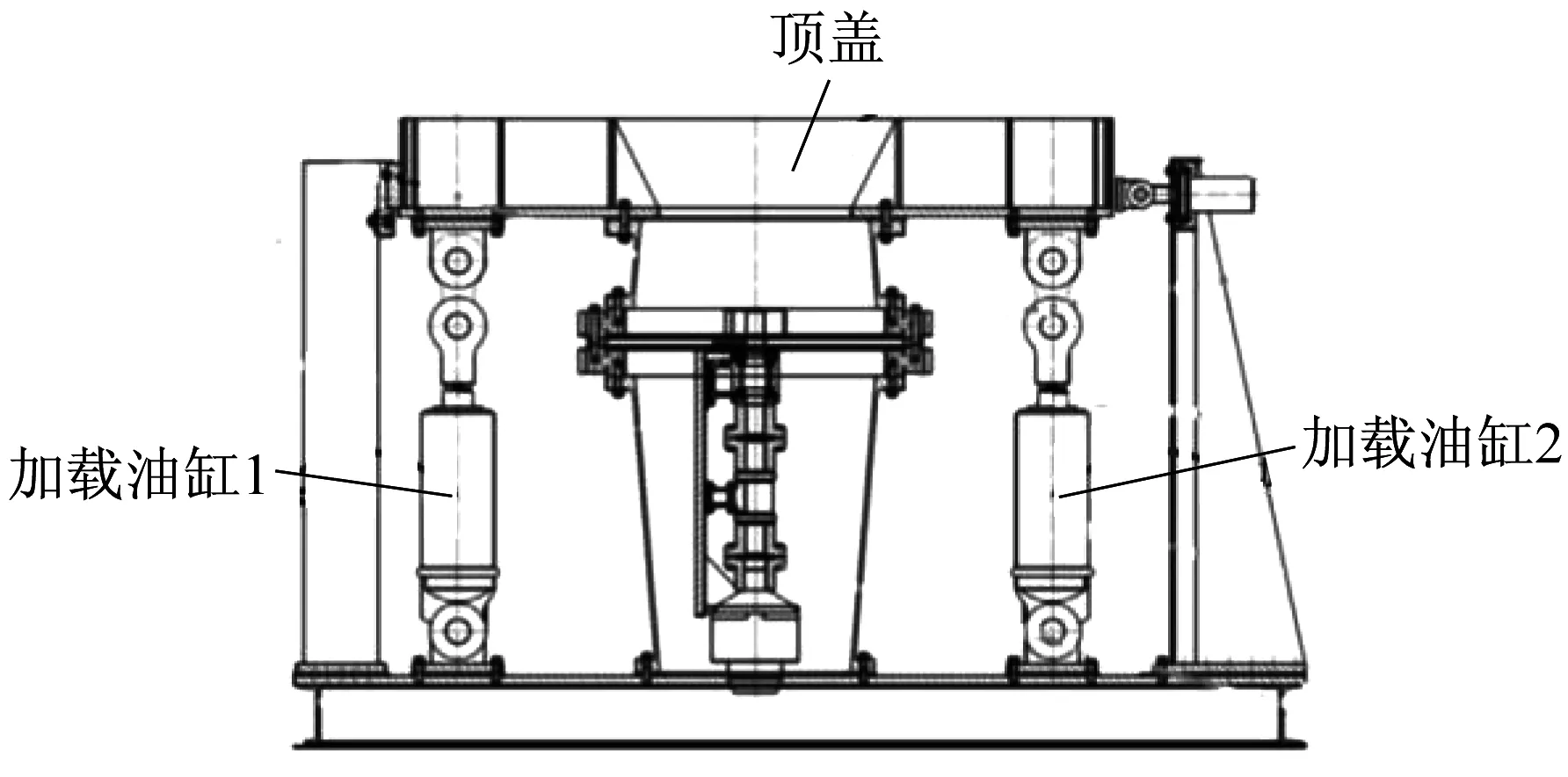
▲图1 回转支承试验台加载油缸
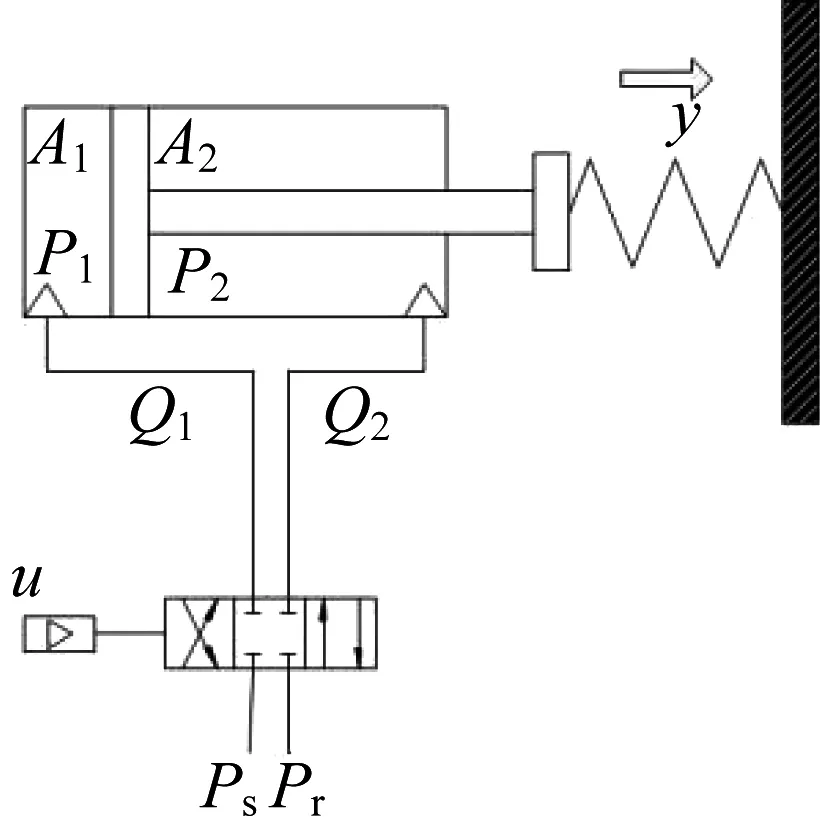
▲图2 加载油缸模型
根据牛顿第二定律,动力学方程为:
(1)
(2)
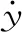
液压缸左右两腔压力动力学方程为:
(3)
(4)
V1=V01+A1y
(5)
V2=V02+A2y
(6)
PL=P1-P2
(7)

Q1、Q2与伺服阀阀芯位移xv有如下关系:
(8)
(9)
(10)
(11)
定义s(·)为:
(12)
式中:Kq1、Kq2分别为伺服阀阀芯位移左右两端流量增益;w1、w2分别为伺服阀阀芯节流孔左右两端面积梯度;Cd为伺服阀节流孔流量因数;ρ为液压油密度;Ps为系统供油压力;Pr为系统回油压力。
对于阀芯位移,用比例环节近似表达为:
xv=kiu
(13)
式中:ki为电压-阀芯位移增益因数;u为输入电压。
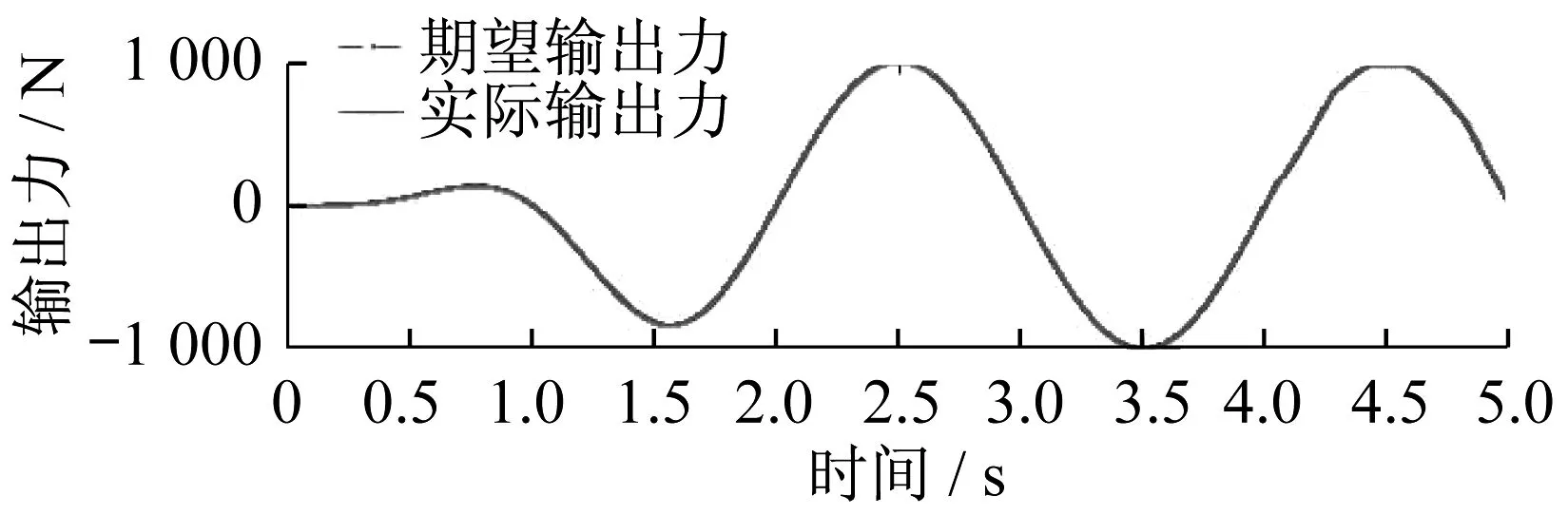
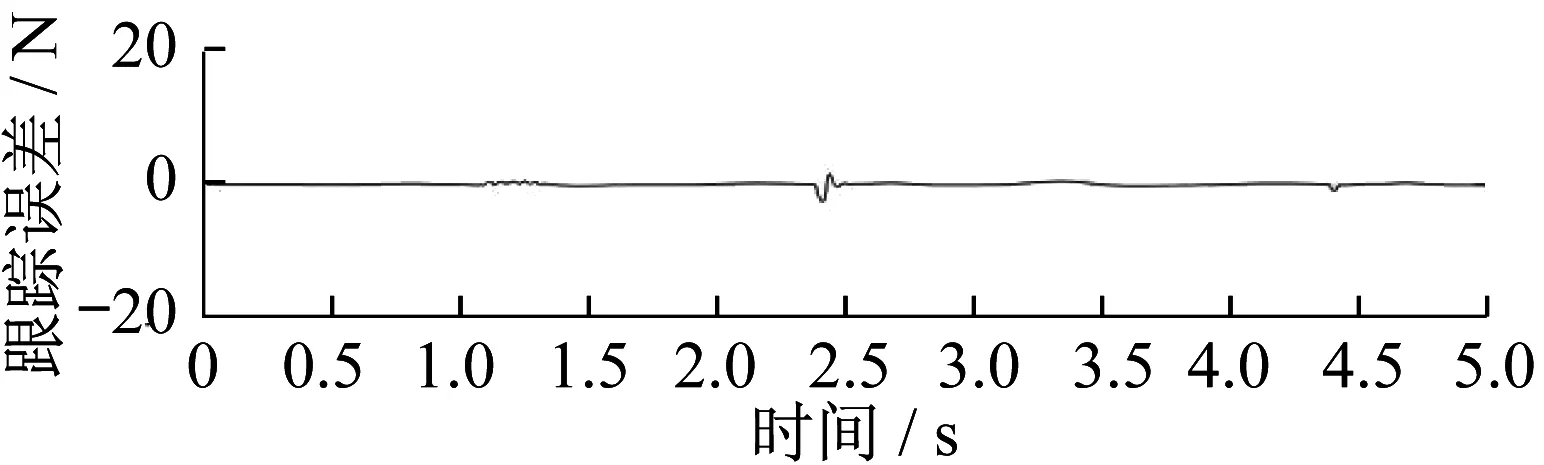
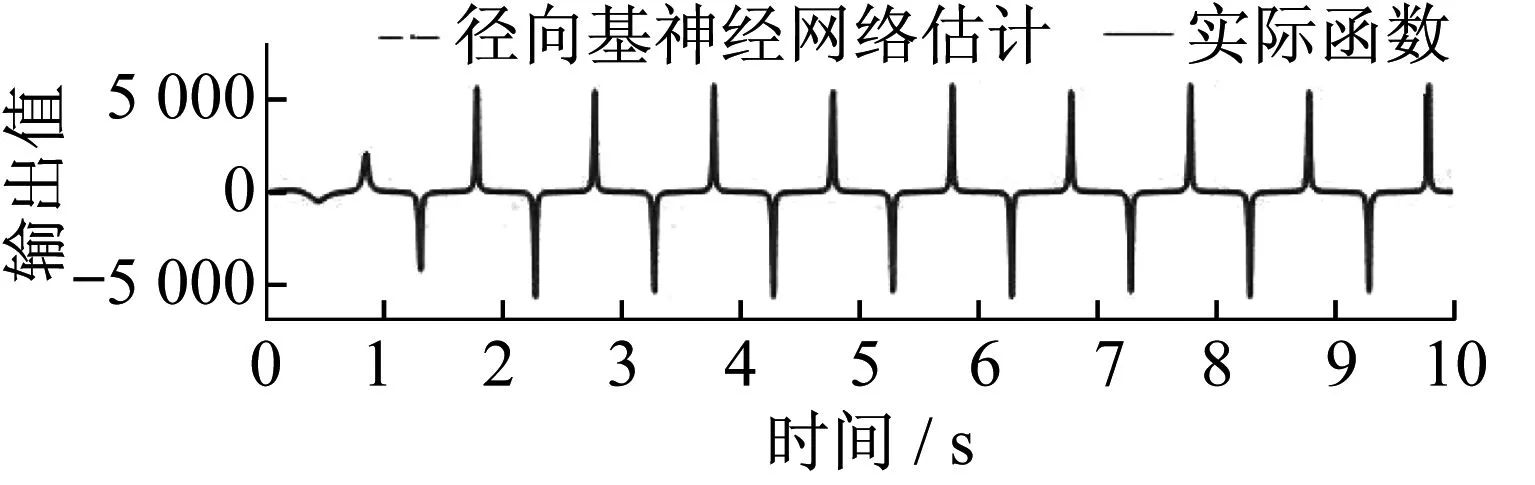
为方便描述系统动力学方程,进行如下简化:假设伺服阀是对称并且匹配的,即Kq1=Kq2=Kq;伺服阀响应速度快于设定值,即伺服阀频宽远高于系统频宽,简化伺服动态为比例环节,有s(xv)=s(u);实际液压系统工作在正常工况下,即液压缸左右两腔压力满足0 令: (14) (15) g=kqki (16) 式(8)、式(9)可描述为: Q1=guR1 (17) Q2=guR2 (18) 根据式(1)、式(2)、式(3)、式(4)、式(17)、式(18)可对力F求导: (19) 为方便描述,令: θ=[θ1,θ2,θ3]T≜[βeg,βe,βeCt]T (20) 规定: (21) (22) (23) 则式(19)可表达为: (24) (25) (26) (27) 式中:j为径向基神经网络隐含层数,x为径向基神经网络输入层向量;cj为中心向量;bj为宽度;hj为径向基神经网络激活函数的输出;ω为估计误差;W*为径向基神经网络隐藏层与输出层之间的最优输出权值。 (28) 则式(24)可以表达为: (29) (30) 式(29)可以表达为: (31) (32) (33) 扰动估计的动力学方程为: (34) 1/ε为扰动观测器的增益。 通常,关于扰动导数的先验信息是未知的,但是有界,至少是局部有界。 为了抑制扰动的有界导数,需要高增益,即ε为低值。 实际上,测量噪声出现在传感器中。如果使用高观测器增益,则噪声被高增益放大,这会导致观测器无法正常工作。为了解决这一问题,引入辅助状态变量ξ,为: (35) 辅助状态变量的动力学方程为: -θ3f3+W*Th(x)] (36) 结合式(32)、式(33)、式(34),可以得到扰动估计误差的动力学方程为: (37) 令: z=F-Fd (38) 式中:Fd为期望轨迹。 则有: =θ1f1u+θ2f2+θ3f3-W*Th(x) (39) 根据式(39)设计控制器[7]: (40) 式中:k1为线性鲁棒反馈增益。 为验证这一控制器的稳定性,引入李雅普诺夫函数VL1: VL1=z2/2 (41) (42) 令: (43) 式(42)可以改写为: (44) 定义李雅普诺夫函数VL2: (45) (46) 式中:γ为辅助变量。 可以得到W权值的自适应率为: (47) 定义李雅普诺夫函数VL3: (48) (49) (50) (51) 为检验所提出的控制策略的有效性,根据电液力伺服系统模型在MATLAB/Simulink软件中搭建系统仿真模型[8-9],系统各物理参数见表1。现实中油缸摩擦力为非连续函数,在仿真中采用连续函数代替,有: (52) 由d=20sint模拟外部扰动,期望输出为: (53) γ为500 000,1-7-1径向基神经网络输入为z,中心值c为[-3 -2 -1 0 1 2 3],宽度b为3。 表1 系统物理参数 输出力曲线如图3所示。 ▲图3 输出力曲线 跟踪误差曲线如图4所示。 ▲图4 跟踪误差曲线 径向基神经网络估计与实际函数对比如图5所示。 ▲图5 径向基神经网络估计与实际函数对比 径向基神经网络逼近误差曲线如图6所示。 ▲图6 径向基神经网络逼近误差曲线 由图3、图4可知,算法的瞬态响应及稳态跟踪性能都十分出色,跟踪误差为0.025%,完全满足实际工程应用要求,可以提高回转支承试验台的加载能力,满足回转支承需要的不同载荷谱[10]。 结合图5、图6得出,对于未知非线性摩擦,径向基神经网络可以精准地进行估计,从而补偿至控制器,提高控制器的跟踪性能。虽然图6中还存在一定的估计误差,但是误差对控制器控制精度的影响很小,对于整个控制器而言是可以接受的。还可以通过增加径向基神经网络隐含层数量和调整中心值的方法来提高径向基神经网络的估计精度,但这同时会增加控制器的计算负荷。 针对回转支承试验台加载过程中因非线性摩擦导致的实际输出与期望输出的误差,笔者提出由径向基神经网络进行估计,并加入补偿,可以实现对非线性摩擦的准确估计,从而消除系统中因非线性摩擦导致的跟踪误差。 笔者提出的算法可以将跟踪误差保持在0.025%以内,大大提高了回转支承试验台加载系统的性能,优于目前试验台4%的跟踪误差。 笔者提出的算法结合了高增益扰动观测器,对系统所受到的扰动及传感器反馈信号中的测量噪声有一定抑制作用,更加贴合实际工况,使算法有更好的实际应用价值。3 神经网络

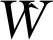
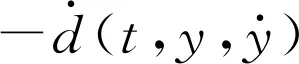
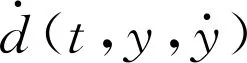

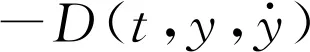
4 高增益扰动观测器

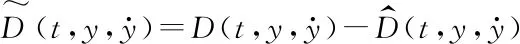

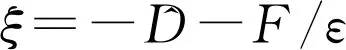

5 控制器设计

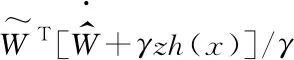
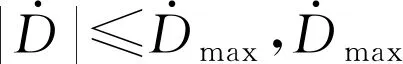
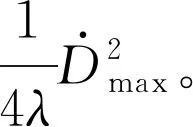
6 仿真分析


7 结束语

