基于极限学习机的电动汽车锂离子动力电池外部短路热模型研究

杨瑞鑫，熊瑞 *，Weixing Shen ，Xinfn Lin

a National Engineering Laboratory for Electric Vehicles, School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China

b Faculty of Science, Engineering and Technology, Swinburne University of Technology, Hawthorn, VIC 3122, Australia

c Department of Mechanical and Aerospace Engineering, University of California, Davis, CA 95616, USA

1.引言

推广电动汽车（EV）是减少全球对化石燃料依赖和减轻环境污染的一项重要举措。可充电锂离子动力电池被认为是电动汽车目前可行的能量来源[1–4]。随着电动汽车的广泛应用，由锂离子动力电池引起的电动汽车安全事故逐渐增多，这些事故对电动汽车和动力电池制造厂商的声誉造成一定影响，损害了公众接受电动汽车的信心。这些安全事故中部分事故是由动力电池的一种电气故障引发的，即外部短路故障。外部短路故障可在某些情况下发生，如电动汽车碰撞导致电池包机械变形、电池包密封失效导致浸水或灰尘进入、动力电池连接线束磨损等。当外部短路故障发生后，动力电池内部发生剧烈的电化学反应，电池温度会急剧升高，可能会进一步触发电池热失控[5,6]。因此，有必要研究动力电池发生外部短路后的温度行为，从而可以有效地进行动力电池安全管理。

1.1.文献综述和本文动机

动力电池在滥用条件下会产生大量热量，众多学者研究了动力电池滥用过程中的放热反应机理和生热特性[7–9]。Ren等[10]开发了一种电化学-热耦合模型，以量化动力电池从过充电到热失控过程中的生热速率。Zhao等[11]利用多尺度电化学-热耦合模型，分析了动力电池针刺过程中的生热行为和电化学反应过程之间的强耦合关系。Chen等[12]提出了一种多层次三维热模型以描述动力电池发生内部短路后电池内外部温度分布。Zhu等[13]通过开展动力电池过充电实验研究了过充电触发热失控的过程，发现电池副反应在发生热失控之前对于温度上升起主导作用。在上述研究中，通过建立复杂的电化学-热耦合模型来描述电池在滥用条件下的热行为。然而，这些模型计算量较大，不能满足电动汽车实际应用中计算效率高的需求。

在动力电池外部短路研究中，学者主要关注外部短路实验方法、热-电行为特性和危害分析、建模和故障诊断等方面[14–21]。Rheinfeld等[14,15]采用准等温外部短路测试方法研究电池材料传输特性对电池外部短路特性的影响，并建立了均质化物理模型来描述外部短路过程。在文献[16,17]中，作者开展了外部短路实验，研究了不同环境温度、电池初始荷电状态（SOC）和外部电阻条件下的电池外部短路的热-电行为特性。Kupper等[18]提出了一种伪三维多尺度模型，分析了在外部短路故障下电池主反应和副反应中的热力学以及动力学过程。本研究团队在前期工作中，建立了分数阶模型来研究外部短路条件下动力电池的电气特性，并提出了外部短路故障的三步诊断方法[19]；提出了针对动力电池组的外部短路在线故障诊断方法，该方法具备较好的准确度和鲁棒性[20]。在文献[21]中，本团队提出了一种基于人工神经网络的外部短路电流预测方法，利用电池电压信息来估计外部短路电池单体的电流。

然而，以上研究缺乏有效的热模型来描述外部短路故障条件下动力电池的温升行为，因此有必要开发一种理想的模型以实现预测精度和计算成本之间的平衡。在电动汽车的实际应用中，由于电池系统空间和制造成本的限制，并非所有动力电池单体都配备温度传感器，因此电池温度应尽可能仅使用电流或电压信息来进行估算。这激励我们开发了一种新颖的电池热模型，以高精度和低计算量来预测外部短路条件下的电池温度，从而完善动力电池外部短路领域的研究。

1.2.原创贡献

本文的创新点包括以下三个方面：①在不同初始SOC值（20%、40%和80%）和不同环境温度（–10 ℃、10 ℃、20 ℃和40 ℃）条件下开展动力电池外部短路实验，并构建外部短路故障数据库，用于建立和验证所提出的电池热模型；②建立基于极限学习机的生热模型（简称ELMT模型）来预测电池发生外部短路后的温度行为。与经典极限学习机相比，ELMT模型中激活函数被集总参数热模型取代，从而更精确地刻画电池温度变化；③在模型拟合和预测精度以及计算成本方面，使用外部短路实验数据对提出的ELMT模型进行验证。为了证明ELMT模型的有效性，比较了ELMT模型与通过遗传算法（GA）优化的MLT模型的性能。

1.3.本文架构

第2节将介绍动力电池外部短路实验平台和分析实验结果。第3节将提出并详细说明ELMT模型。在第4节中，使用不同初始SOC值和环境温度下的外部短路数据验证所提出的模型。第5节为本文结论。

2.实验研究

为研究外部短路条件下动力电池的电、热行为特性，本文在不同实验条件下开展了电池外部短路测试。这些条件涵盖了高、中和低的环境温度（分别为40 ℃、20 ℃、10 ℃和–10 ℃），以及高、中和低的电池初始SOC值（分别为80%、40%和20%）。在每种实验条件下，重复进行两次外部短路测试，实验结果分别用第1组和第2组实验结果表示。将实验数据用于训练和验证本文提出的模型。表1为本文所使用的18650型Li(Ni0.5Co0.2Mn0.3)O2电池的详细规格。

表1 镍钴锰三元材料锂离子电池规格

2.1.外部短路实验平台

本文进行了如图1所示的外部短路实验，该平台用于开展动力电池外部短路实验并研究电池外部短路行为特性。在前期工作[20]中，我们已经建立了一种电池组外部短路实验平台并已对其进行详细阐述。本文重点关注动力电池单体外部短路实验，该平台主要包括以下几部分：① 气动电池外部短路实验控制主机；② 为控制主机提供气源的空气压缩机；③ 防爆高低温试验箱；④ 电流、电压和温度传感器；⑤ 高精度数据采集仪。

在数据采集仪器开启并记录实验数据后，接触器（图1）由外部短路主机控制闭合，接触器闭合后动力电池的正极和负极在电池外部直接连接，从而模拟电动汽车在实际应用中的外部短路故障。同时，电池电流、电压和温度信息由相应的传感器测量并存储至数据采集仪。当电流和电压降低到0 A和0 V时表示电池已损坏，此时手动开启接触器，实验结束。

图1.动力电池外部短路实验平台。

2.2.实验结果分析

动力电池外部短路电流和温度的实验结果如图2和图3所示。图2（a）、（b）分别显示了在环境温度20 ℃和40 ℃，初始SOC值20%、60%和80%的条件下第1组实验中的电池电流和温度结果；图2（c）、（d）分别显示了在环境温度10 ℃和–10 ℃，初始SOC值20%、60%和80%的条件下第1组实验中电池电流和温度结果。同理，图3显示了在不同环境温度和不同初始SOC值下动力电池第2组的外部短路实验结果。如图2和图3所示，当发生外部短路后，动力电池电流在1 s内迅速增加，峰值电流可达到近150 A（约61 C-rate）。大电流自放电产生的焦耳热积聚在电池内部，导致电池温度迅速升高。电池电流达到峰值后，逐渐减小。如文献[18]所述，电流达到峰值后逐渐减小的原因是，高温可能导致电池隔膜产生“闭孔”效应，从而降低了锂离子的扩散和迁移速率。随后，电池经历了“放电平台期”（discharge plateau），最后电流降至0 A，表明电池已损坏。

从图2和图3的实验结果可以得到以下结论：①相同环境温度和初始SOC值条件下，两组的实验结果显示出良好的可重复性；②在相同的环境温度下，初始SOC值较低的电池的放电时间比初始SOC值较高的电池更长；③具有较高初始SOC值的电池在所有环境温度下的温升速率相对较大。此外，我们前期的研究工作也总结分析了其他外部短路相关测试结果[19–21]。

3.电池建模与生热行为估计

3.1.集总参数热模型

集总参数热模型可以用来描述动力电池的生热行为，该模型假设电池内部温度分布均匀。根据能量守恒定律，电池总产热量等于对流换热量与生热量之和，具体可以表示为：

式中，h为对流换热系数；Tamb为环境温度；T为电池温度；Cp、V、A、ρ和t分别表示电池比热容、体积、表面积、密度和时间；q为电池生热量，根据文献[22,23]，可以由下式计算：

图2.不同温度和初始SOC值下动力电池电流和温度结果（第一组）。（a）20 ℃和40 ℃下的电流；（b）20 ℃和40 ℃下的温度；（c）–10 ℃和10 ℃的电流；（d）–10 ℃和10 ℃的温度。

图3.不同温度和初始SOC值下动力电池电流和温度结果（第二组）。（a）20 ℃和40 ℃下的电流；（b）20 ℃和40 ℃下的温度；（c）–10 ℃和10 ℃的电流；（d）–10 ℃和10 ℃的温度。

式中，i表示不可逆反应生热；ILT(dU0/dT)表示可逆反应生热；IL为电流；Ri为电池内部总内阻；Uo表示电池开路电压。总体来说，不可逆反应生热包括以下两个部分：① 电流流经集流体和固态电解质界面（SEI）膜所产生的焦耳热；②由过电势带来的极化反应产热。可逆反应生热主要由电池电化学反应产生，是由锂离子在电池内部的正、负极材料中的嵌入或脱嵌过程所引起的。

在公式（2）中，研究人员已经证明了在外部短路条件下电池可逆反应生热远小于不可逆反应生热[16]。在本文中，为进一步证明可逆反应生热占比较小，我们利用第一组实验中的电池外部短路数据（初始SOC值为40%，环境温度为20 ℃）来计算和对比可逆与不可逆反应生热。图4（a）、（b）分别表示了测量得到的熵热系数dU0/dT以及可逆与不可逆反应生热的对比结果。

图4.动力电池生热测试与计算结果。（a）熵热系数；（b）可逆与不可逆反应生热。

从图4（b）可以看到，不可逆反应生热i远大于可逆反应生热ILT(dU0/dT)。因此，公式（2）中的ILT(dU0/dT)可以被忽略。随后，将简化后的公式（2）代入公式（1）中可得到

式中，Tk表示k时刻下的电池温度；Δt为采样时间间隔。

3.2.极限学习机

Huang等[24]首次提出了经典极限学习机，极限学习机克服了单隐含层前馈神经网络的部分缺点，即训练速度慢、容易陷入局部极小值以及对学习速率敏感等。经典极限学习机的结构如图5所示。由于连接输入层与隐含层之间的权值以及隐含层中的阈值可随机生成，训练过程中无需迭代调整，只需根据训练数据确定隐含层与输出层之间的连接权值，因此该方法计算效率较高 [25]。

极限学习机的输入向量X和输出向量Y可以定义为

式中，x和y分别为输入和输出数据；n和m分别表示输入层和输出层的总数据量。

极限学习机的构建流程如下：

步骤1：确定隐含层神经元节点数量，l。

步骤2：随机生成输入层与隐含层之间的连接权值w以及隐含层中的阈值b。权值矩阵w和阈值向量b可以表示为

步骤3：选择一种激活函数用于计算输出层的输出。

图5.经典极限学习机结构图。x和y表示输入和输出数据；n和m为输入层和输出层的总数据量；w为输入层和隐含层之间的连接权值；βjs为隐含层和输出层之间的连接权值；g(∙)表示激活函数；b表示隐含层中的阈值；i表示第i个输入数据；j表示第j个隐含层神经元；s表示第s个输出数据。

式中，βjs为隐含层和输出层之间的连接权值；s为输出层第s个节点（s= 1, 2,...,m）；i为输入层第i个节点；j为隐含层中第j个节点。如果定义连接权值矩阵β为

公式（6）可以表达为矩阵形式

步骤4：确定隐含层与输出层之间的连接权值。权值矩阵β可以通过求解以下方程组的最小二乘解获得，其中Y*为测量数据矩阵。

其解为

式中，H+为输出矩阵H的Moore-Penrose广义逆。

3.3.基于极限学习机的电池热模型

在经典极限学习机中，激活函数通常是高度非线性且连续可微的，包括S型函数、双曲正切函数和高斯函数等[24]。但通过学者多年的深入研究，已经证明激活函数可以是任意非线性函数，甚至可以是不连续或不可微的形式[25–28]。

在本文中，结合具备实际物理意义的集总参数热模型与经典极限学习机，提出一种基于极限学习机的生热模型，即ELMT模型，来描述动力电池在外部短路条件下的温度行为。具体来说，将经典极限学习机中的激活函数替换为3.1节中介绍的集总参数热模型。ELMT模型的结构如图6所示，其中使用L个集总参数子模型。将电流Ik作为模型输入，温度Tk+1作为模型输出(k= 1, 2,…,N–1)，N–1表示温度输出数据的总量。L个集总参数子模型可以被视为极限学习机中的激活函数。

基于集总参数热模型公式（3）和极限学习机公式（6），电池温度Tk+1可以表达为

式中，j表示第j个子模型（j= 1, 2,...,L）；Hk,j为隐含层中第j个子模型的输出。其他参数在3.1节中已经介绍。Hk+1,j的迭代形式可以表达为

因此，公式（11）可以表达为

图6.基于极限学习机的生热模型原理图。

公式（13）表达了每一时刻温度的输出结果可以通过L个子模型输出加权后求和得到。在每个集总参数子模型中，可以直接测量电池质量、表面积A和环境温度Tamb。未知的参数矩阵P可以表达为

在L个子模型中共有3 ×L个参数有待确定。根据极限学习机的原理，上述参数可以在一定范围内随机生成且训练过程中无需迭代调整，这样可以极大降低模型参数化的计算复杂度。上述参数范围可以根据先验知识获得[29,30]，例如，h在强制对流换热条件下的取值范围为10～200 W·m–2·K–1。因此，参数取值范围如表2所示，通过设定较宽的参数取值范围以涵盖各种电池外部短路条件并取得最优解。

表2 集总参数热模型参数取值范围

隐含层与输出层之间的连接权值βj可以通过拟合实测温度与模型输出之间的最小二乘解确定。在本文中，考虑计算复杂度与模型精度，集总参数子模型数量可以设置为20，即L= 20。

ELMT模型的优势如下：

（1）与一般的机器学习模型相比，ELMT模型极大地提高了计算效率，原因是其在训练过程中无需迭代调整公式（14）中的参数；

（2）由于ELMT模型是一种神经网络模型，因此与简单集总参数热模型相比，通过拟合训练数据可以获得更高的模型精度；

（3）与经典极限学习机相比，ELMT模型采用集总参数热模型来代替激活函数，因此更具有实际物理意义，同时可以基于先验知识确定模型参数中w和b的取值范围；

（4）将热模型和经典极限学习机结合的方法扩展应用到其他难以确定参数的电池模型中，如电化学模型，通过设置合理的参数取值范围，可以使模型精度较高。

3.4.多集总参数热模型

为了证明ELMT模型的优势，将MLT模型作为对照模型。MLT模型的结构与图6所示的ELMT模型相同，然而Ri、h、Cp和βj需要进行迭代调整以逼近实验数据。为公平比较，MLT模型由5个集总参数热模型组成，因此MLT模型中共有20个可调参数，这与ELMT模型中的可调参数（连接隐含层与输出层之间的20个权重βj）相同。

MLT模型参数采用遗传算法辨识得到，遗传算法是一种常用的非线性启发式优化算法[29]。在遗传算法中，不断优化模型参数以最小化以下目标函数：

式中，Test为估计温度；Tmea为测量温度。

综上所述，ELMT模型和MLT模型中共有20个可调参数，两模型之间的主要区别在于参数的获取方法：ELMT模型参数是通过单次最小二乘求解获得的，无需迭代调整；MLT模型的所有参数是通过不断迭代优化获得的。

4.模型验证与评价

在本节中，使用第2节中得到的动力电池外部短路实验数据来验证和评价所提出的ELMT模型。利用第1组实验数据对模型进行训练，以检验模型拟合动力电池外部短路温度的精度；利用第2组实验数据评价模型对动力电池外部短路温度的预测精度。在所有模型拟合和预测的评价中，对ELMT模型和MLT模型进行对比分析。

4.1.拟合精度分析

为评价模型描述外部短路条件下电池温度行为的性能，利用第1组实验数据检验ELMT模型拟合电池温度的精度。图7显示了在环境温度为40 ℃和20 ℃以及初始SOC值为80%，40%和20%的条件下，ELMT模型和MLT模型的温度拟合结果；图8显示了在环境温度为10 ℃和–10 ℃以及与图7相同的初始SOC值条件下，两模型的温度拟合结果。此外，在每个子图中，插图（i）表示ELMT模型的温度拟合误差，插图（ii）表示MLT模型的温度拟合误差。可以看出，ELMT模型的温度拟合误差均小于4 ℃，而MLT模型的温度拟合误差可以高达25 ℃。

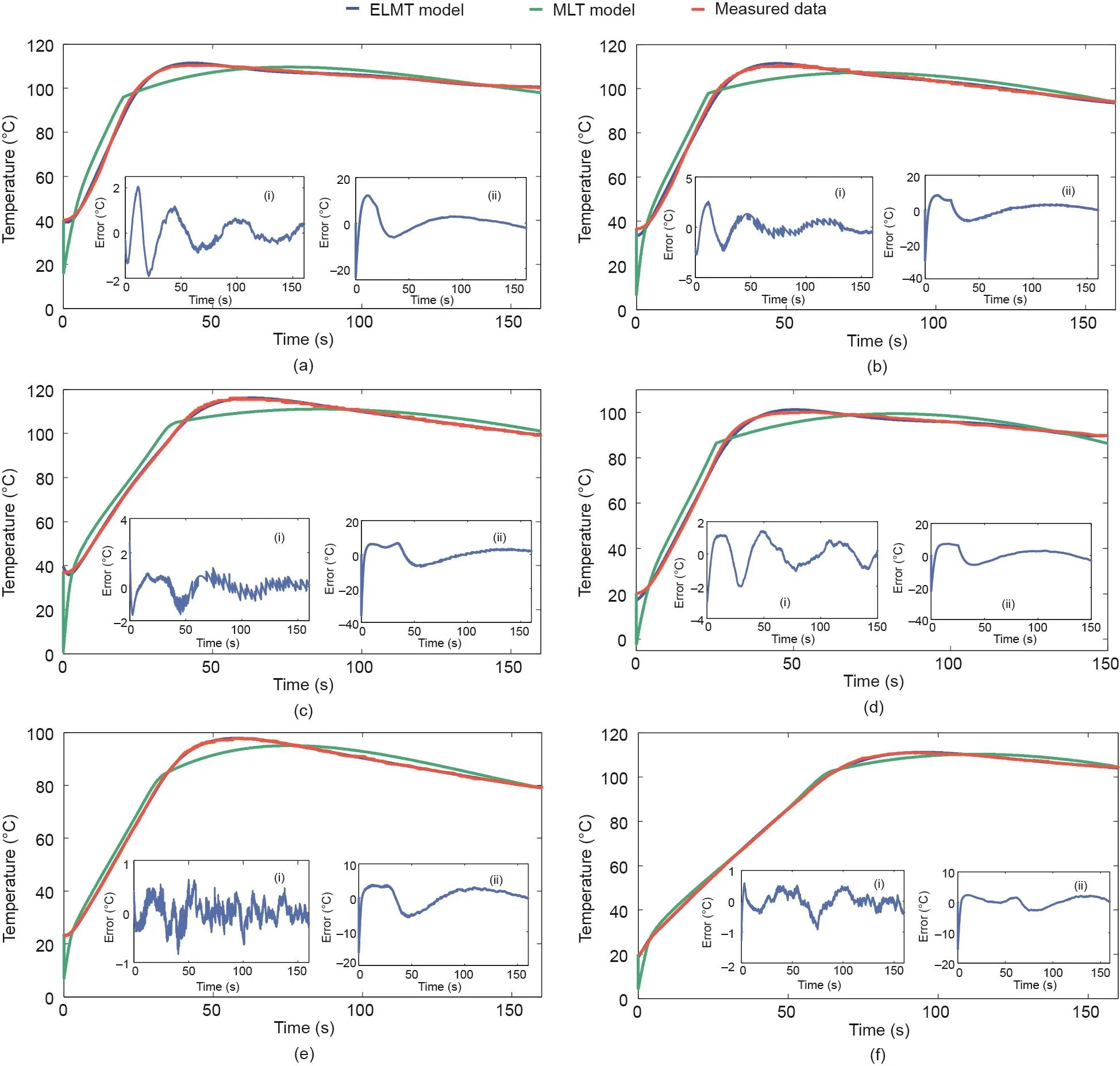
图7.不同初始SOC值和环境温度（40 ℃和20 ℃）下模型的温度拟合结果。（a）40 ℃时80% SOC；（b）40 ℃时40% SOC；（c）40 ℃时20% SOC；（d）20 ℃时80% SOC；（e）20 ℃时40% SOC；（f）20 ℃时20% SOC。

表3比较了两种模型在不同条件下的温度拟合结果与实测温度之间的均方根误差（RMSE）；表4列出了每种环境温度以及所有条件下两种模型温度拟合的RMSE平均结果。可以看出，在所有条件下，ELMT模型比MLT模型具有更好的拟合精度，其中，ELMT模型的RMSE平均值为0.65 ℃，而MLT模型的RMSE平均值为3.95 ℃（表4）。因此，与具有相同数量可调参数的MLT模型相比，ELMT模型拟合不同条件下动力电池外部短路的温度行为具备更优异的性能。

表3 不同条件下模型温度拟合的RMSE结果对比

表4 不同环境温度下模型温度拟合的RMSE平均结果对比

进一步分析两种模型训练过程的计算效率。在不同外部短路条件下，两种模型的训练时间如表5所示。训练时间是基于MATLAB 2013b（MathWorks, USA）平台，计算从程序开始到结束的所用时间。程序运行使用的计算机配置为Thinkpad T470（Intel®CoreTMi7-7700HQ CPU 2.8GHz, RAM 16GB, SSD 500G）。

表5 不同条件下模型的计算时间对比

显然，ELMT模型相比MLT模型的训练所用时间更少。如前所述，ELMT模型具有更高计算效率的原因在于大部分参数在训练前随机生成，无需在训练过程中迭代调整。相比之下，MLT模型参数是通过使用遗传算法不断迭代求得的。

4.2.预测精度分析

由于第2组外部短路实验数据未参与模型训练过程，因此使用第2组实验数据评价ELMT模型对于动力电池外部短路温度预测的准确性。同样地，利用MLT模型进行对比分析。

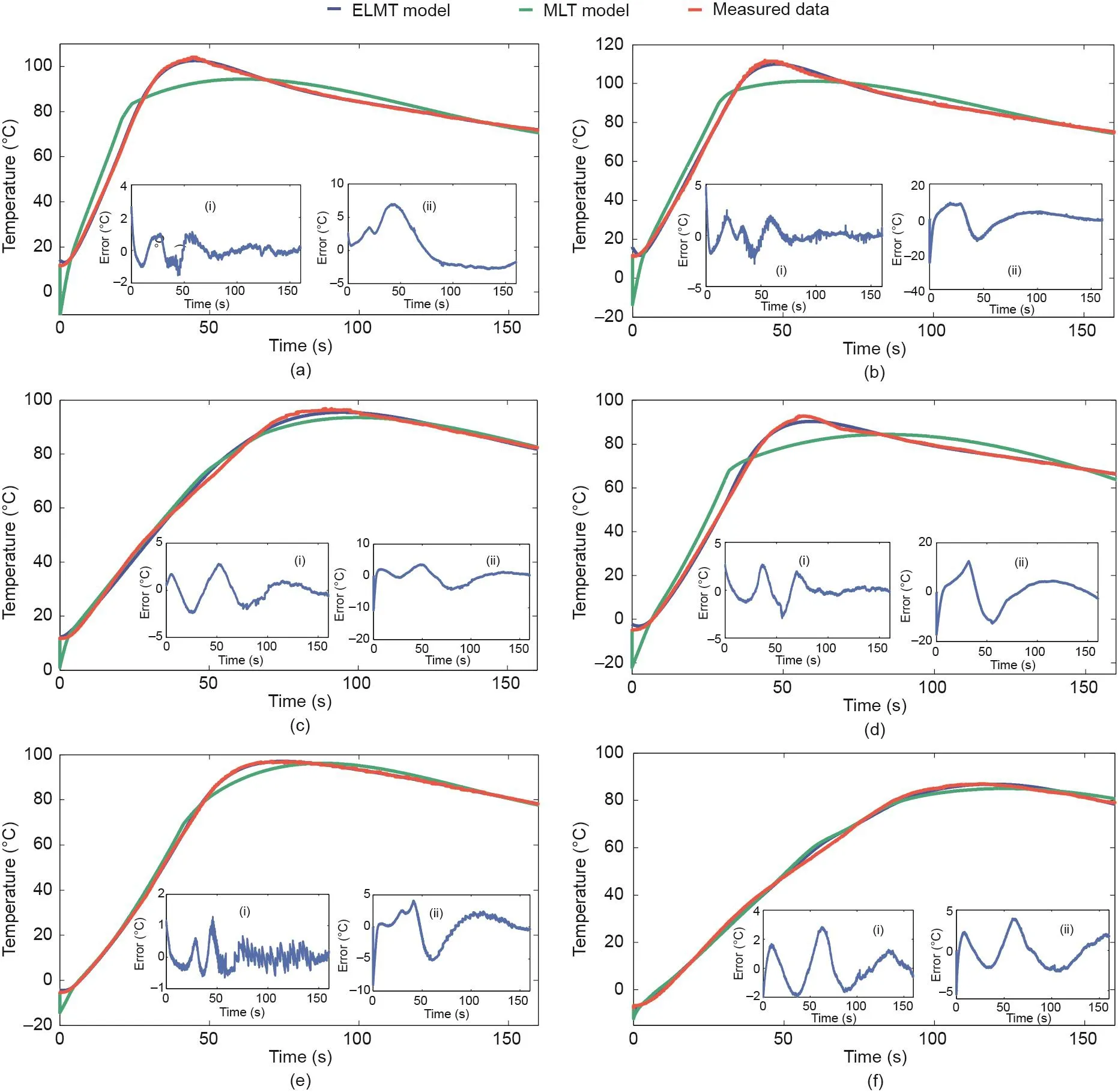
图8.不同初始SOC值和环境温度（10 ℃和–10 ℃）下模型的温度拟合结果。（a）10 ℃时80% SOC；（b）10 ℃时40% SOC；（c）10 ℃时20% SOC；（d）–10 ℃时80% SOC；（e）–10 ℃时40% SOC；（f）–10 ℃时20% SOC。

图9显示了两种模型在40 ℃和20 ℃以及在三种不同初始SOC值条件下的电池温度预测结果。图10显示了在10 ℃和–10 ℃以及相同SOC值条件下的电池温度预测结果。在图9和图10子图中，插图（i）表示ELMT模型的外部短路温度预测误差结果；插图（ii）表示MLT模型的外部短路温度预测误差结果。

表6显示了两种模型在不同SOC值和环境温度下的温度预测值与测量值之间RMSE结果的比较。表7显示了在不同环境温度以及所有条件下温度预测的RMSE平均结果比较。如表7所示，ELMT模型所有条件下的RMSE平均值仅为3.97 ℃，而MLT模型所有条件下的RMSE平均值为6.11 ℃。可以发现，ELMT模型相比MLT模型具有更高的温度预测精度。

表6 不同条件下模型预测的RMSE结果对比

表7 不同环境温度下模型预测的RMSE平均结果对比

图9.不同初始SOC值和环境温度（40 ℃和20 ℃）下模型的温度预测结果。（a）40 ℃时80% SOC；（b）40 ℃时40% SOC；（c）40 ℃时20% SOC；（d）20 ℃时80% SOC；（e）20 ℃时40% SOC；（f）20 ℃时20% SOC。

图10.不同初始SOC值和环境温度（10 ℃和–10 ℃）下模型的温度预测结果。（a）10 ℃时80% SOC；（b）10 ℃时40% SOC；（c）10 ℃时20%SOC；（d）–10 ℃时80% SOC；（e）–10 ℃时40% SOC；（f）–10 ℃时20% SOC。

5.结论

本文提出了一种ELMT模型以刻画在不同外部短路条件下动力电池的温度行为，在ELMT模型中，利用基于物理意义的集总参数热模型替代经典极限学习机中的激活函数。在不同环境温度（40 ℃、20 ℃、10 ℃和–10 ℃）和电池初始SOC值（80%、40%和20%）下系统地开展了动力电池的外部短路实验，构建了外部短路故障数据库以建立和评估所提出的模型。为证明所提出模型的优势，比较了ELMT模型与遗传算法参数化的MLT模型。通过使用两种模型拟合训练数据（第1组实验数据）中电池外部短路后的温度，比较了两种模型的拟合精度。在所有实验条件下，ELMT模型拟合温度的RMSE平均值为0.65 ℃，MLT模型拟合温度的RMSE平均值为3.95 ℃。此外，还比较了两种模型的计算时间，并证明了ELMT模型相比MLT模型具有更低的计算成本。在模型预测电池外部短路温度方面，使用第2组外部短路实验数据进一步评估两个模型的预测精度。在所有实验条件下，ELMT模型预测温度的RMSE平均值为3.97 ℃，而MLT模型预测温度的RMSE平均值为6.11 ℃。以上结果表明，与MLT模型相比，ELMT模型具有更好的拟合和预测精度以及较高的计算效率。

未来的研究工作包括：① 研究外部短路过程中电池阶段性损伤特性；② 提高ELMT模型的泛化能力以更好地预测电池内部温度。

致谢

本研究得到了国家重点研发计划（2018YFB0104100）和国家留学基金委员会的支持。动力电池外部短路实验在北京理工大学先进储能科学与应用（AESA）课题组实施完成。

Compliance with ethics guidelines

Ruixin Yang, Rui Xiong, Weixiang Shen, and Xinfan Lin declare that they have no conflict of interest or financial conflicts to disclose.