汽轮机转子钢低周疲劳数据批量化处理方法

代海燕 田 宇 王丽艳 马新博

(哈尔滨汽轮机厂有限责任公司，黑龙江150046)

近年来，随着大功率高容量机组的增加以及电站频繁调峰的需求，对汽轮机转子体积、启停和变工况次数提出了更高的要求[1]。汽轮机转子作为大型铸锻件，不仅体积庞大、结构复杂，转子表面还存在一些容易引起应力集中的非平滑过渡区域。而汽轮机启动、停机、变工况和超速运转过程中，由于热应力、离心力等联合作用，应力集中区的局部应力往往超过转子材料的屈服应力，使应力集中区进入塑性状态，形成一个或大或小的塑性区[3-4]。在低频交变载荷的作用下，塑性区首先形成低周疲劳裂纹源，材料在远低于屈服强度的应力水平下就会发生疲劳破坏[5-6]。因此，汽轮机转子钢的低周疲劳寿命分析一直是汽轮机设计部门和生产测试部门研究的重要课题。

汽轮机转子钢的低周疲劳性能评价和构件寿命预测都依赖于材料或构件的低周疲劳试验。尤其是新型转子钢，如14Cr9Mo1.5Co1.2NbNB、13Cr10.5Mo1.5NiVNbN、14Cr10.5Mo1W1NiVNbN等不同温度等级的转子钢，其转子钢材料在各个温度下的低周疲劳试验测试量很大，试验结果分析处理过程中需要输入的试验数据量非常大。

传统的低周疲劳数据分析方法一般使用Basic语言、C语言等，使用时需手动输入试验值，而微应变需要输入小数点后四位，而寿命值可能需要输入5位数字，因此容易出现输入错误的情况，影响试验分析结果；且传统编程方法所得到的图像不能进行二次编辑，处理过程的变量值不直观，拟合曲线数值不能直接导出。本文中的低周疲劳数据分析方法，可以实现对大规模数据的可复制输入，并且处理结果过程中能得到可以直接进行编辑的图像模式，处理过程的变量值直观，能够导出拟合曲线数值，稳定高效地实现了汽轮机转子钢低周疲劳数据的批量化处理。

1 理论模型

低周疲劳试验的主要目的是得到测试材料的应变和寿命之间的关系。由于转子钢材料以恒定的应变幅加载时，施加在材料上的应力和设定的实验应变值之间存在一定的滞回关系，因此低周疲劳试验数据分析处理的主要方法是采用Masson-Coffin公式[7-8]。总应变Δεt、弹性应变Δεe、塑性应变Δεp满足以下关系：

Δεt=Δεe+Δεp

(1)

Δεe=2σf′(2Nf)b/E

(2)

Δεp=2εf′(2Nf)c

(3)

式中，E为扬氏弹性模量，σf′、b分别为疲劳强度系数和疲劳强度指数，εf′、c分别为疲劳延性系数和疲劳延性指数。

比较稳定应力-应变曲线与静拉伸应力-应变曲线，便可显示出循环引起材料的变形特性和程度，以此判断材料是循环软化还是循环硬化。循环应力-应变特性可表示为Ramberg-Osgood公式[5]：

Δσ=2K′(ΔεP/2)n′

(4)

式中，K′为循环强度系数，表征材料产生单位循环塑性变形时的真实应力；n′为循环应变硬化指数，表征材料产生塑性变形的能力。

2 程序设计

2.1 原始数据分块

根据低周疲劳试验过程中MTS试验机获得的试验记录数据，对试验报告中记录的总应变量，疲劳寿命，最大应力，最小应力，弹性模量数组信息复制后生成总数据矩阵D；总应变Et为矩阵D的第一列，D1；疲劳寿命halfNf为矩阵D的第二列，D2；试验中的最大应力max_stress为矩阵D的第三列，D3；最小应力min_stress为矩阵D的第四列，D4；弹性模量E为矩阵D的第五列，D5。

将总数据矩阵D中各个列处理成Masson-Coffin公式指数形式的所需数值后分别存为各个列矩阵。

相关的编程程序语句为：

Et=Data(:,1);

halfNf=Data(:,2);

max_stress=Data(:,3);

min_stress=Data(:,4);

E=Data(:,5);

Nf=halfNf*2

2.2 调用拟合函数

调用polyfit函数，对弹性应变Ee-2倍的疲劳寿命Nf做线性拟合，p(1,1)为拟合直线的斜率，即为疲劳强度指数b，p(1,2)为拟合直线的截距，可转化为疲劳强度系数Dfe；对塑性应变Ep-2倍的疲劳寿命Nf做线性拟合，q(1,1)为拟合直线的斜率，即为疲劳延性指数c，q(1,2)为拟合直线的截距，可转化为疲劳延性系数Ef；对应力均值stress-塑性应变Ee做线性拟合，r(1,1)为拟合直线的斜率，即为循环应变硬化指数，r(1,2)为拟合直线的截距，可转化为循环强度系数K。

相关的编程语句为：

Ee1=log(Ee)/log(10);

Nf1=log(Nf)/log(10);

p=polyfit(Nf1,Ee1,1);

b=p(1,1);

Dfe=10^p(1,2);

Ep1=log(Ep)/log(10);

q=polyfit(Nf1,Ep1,1);

c=q(1,1);

Ef=10^q(1,2);

stress1=log(stress)/log(10);

r=polyfit(Ep1,stress1,1);

n=r(1,1);

K=10^r(1,2)

2.3 生成曲线

设置空的结果矩阵，将疲劳强度性能数据所得到的数值存入矩阵当中；设置横坐标点，计算弹性应变-疲劳寿命曲线绘图点的纵横坐标值；调用plot函数，设置绘图的线型、颜色等，绘制弹性应变-疲劳寿命图；绘制塑性应变-疲劳寿命图。

相关的编程语句为：

plot(x,y33,′k-′,x,y11,′r-′,x,y22,′b-′,′linewidth′,2.0);

hold on;

plot(Nf,Et,′ko′,Nf,Ee,′ro′,Nf,Ep,′bo′);

set(gca,′Yscale′,′log′);

set(gca,′Xscale′,′log′);

xlabel(′2Nf/cylcle′);

ylabel(′strain/mm/mm′);

legend(′总应变′,′弹性应变′,′塑性应变′,3);

figure

plot(Ep,stress,′ro′);

hold on;

plot(x2,yy,′r-′);

set(gca,′Yscale′,′log′);

set(gca,′Xscale′,′log′);

xlabel(′Ep/mm/mm′);

ylabel(′Stress/MPa′)

3 程序运行

基于某转子钢高温下的低周疲劳试验时MTS试验机记录的数据结果见表1。

带入编制的处理程序后，运行窗口和结果显示如图1所示。

经本低周疲劳试验处理程序后的试验结果为Dfe=0.0033542，结果上限为0.0034256，下限为0.0032843；b=-0.045145；Ef=0.47909，结果上限为0.61692，下限为0.37206；c=-0.1897；K=665.62，结果上限为684.2，下限为647.54；n=0.069185。

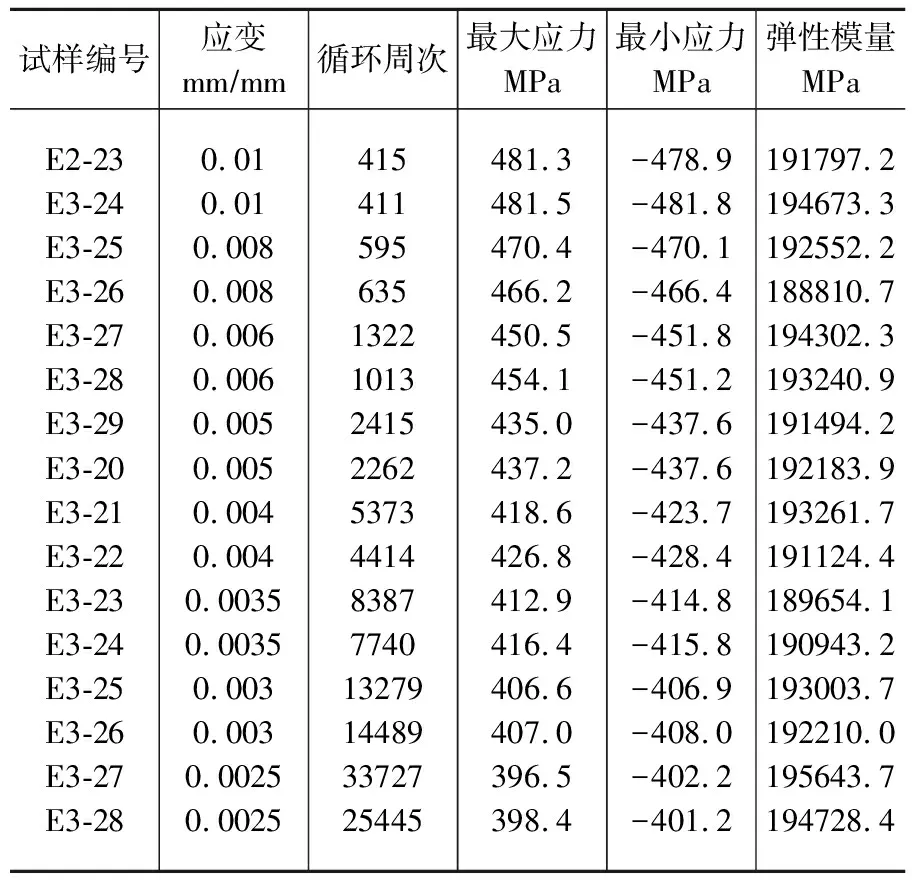
表1 MTS试验机记录的低周疲劳数据结果Table 1 Low cycle fatigue data recordedby MTS testing machine

图1 数据处理程序执行窗口Figure 1 Data processing program execution window

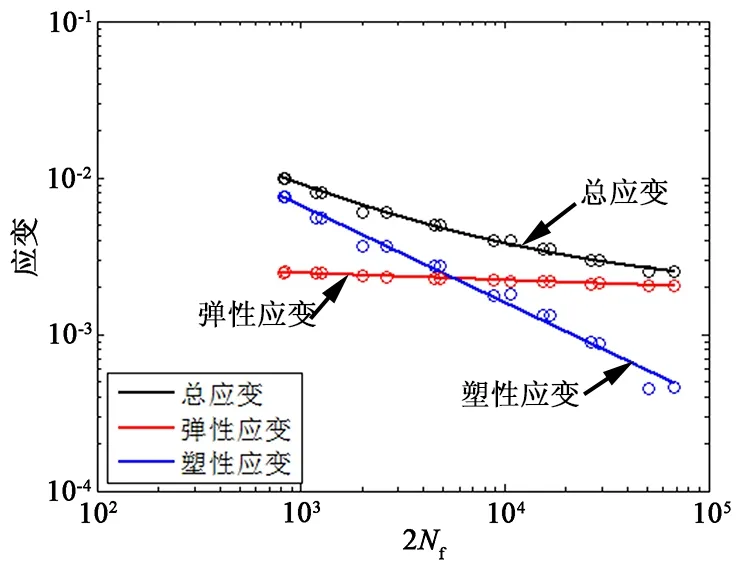
图2 寿命-应变曲线Figure 2 Life-strain curve

绘制疲劳寿命-应变图像上的散点。保持绘图界面不动，绘制三组散点，其中疲劳寿命-弹性应变散点组、疲劳寿命-塑性应变散点组、疲劳寿命-总应变散点组里各点的纵横坐标值分别来源于列矩阵Nf2和列矩阵Ee、列矩阵Nf2和列矩阵Ep、列矩阵Nf2和列矩阵Et，设置散点的形状，得到寿命应变曲线如图2所示。

调用数据处理程序中figure命令再新建一个绘图窗口，以列矩阵Ep和列矩阵stress分别为曲线上点的横坐标值和纵坐标值，调用plot函数绘制塑性应变-稳定循环应力曲线图，如图3所示。

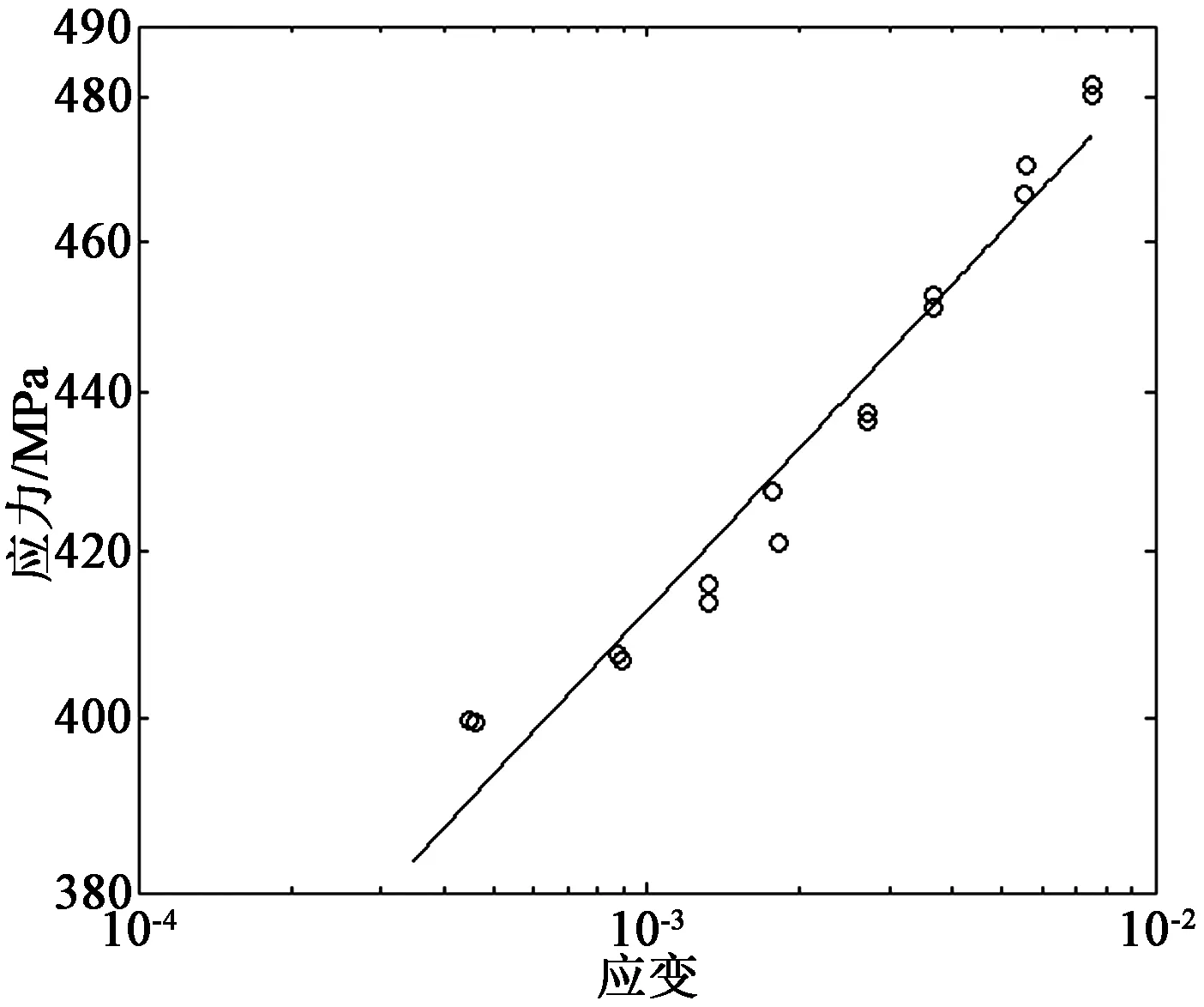
图3 塑性应变-应力曲线Figure 3 Plastic strain-stress curve

4 总结

利用数据处理程序进行低周疲劳数据处理编程，简化输入过程，可以高效地得到疲劳强度指数，将数据存成各个列向量，数据处理结果更加直观，方便导出；程序自绘图后调用图像工具箱，利用工具箱强大的图像编辑处理功能直接处理曲线，避免了导出数据到origin/excel等画图软件再次编辑的麻烦，为高效快速的低周疲劳数据处理分析提供了技术手段。