地震作用下考虑桥台-土相互作用的多跨简支板梁桥碰撞效应研究
邓育林 魏 征 葛 雄
(武汉理工大学交通学院 武汉 430063)
0 引 言
震害调查表明,梁体与桥台背墙间的碰撞是桥梁典型震害表现,碰撞易引起桥台多种破坏,包括台身倾斜、台后土体失效、台背墙断裂以及桥台桩基破坏等[1].且由于桥台的失效与破坏,主梁还可能因为过大的地震位移而发生落梁[2-3].为了解碰撞对桥梁结构抗震性能的影响,国内外学者进行了大量研究,Bi等[4]研究了模块化伸缩缝(MEJ)在桥台和桥面板之间避免碰撞所需的最小总间隙;邓育林等[5]采用非线性时程法对地震作用下大跨度桥梁伸缩缝处碰撞效应进行了研究;王军文等[6]采用三维精细化计算模型分析了地震作用下斜度、摩擦对斜交简支梁桥纵向碰撞响应的影响;陈彦江等[7]对简支梁桥碰撞效应的影响因素进行了动力非线性时程反应分析;Rezaei等[8]采用概率地震评估方法,研究了碰撞对四种不同高度不平顺混凝土箱梁桥抗震性能的影响;Shi等[9]对比分析了桥梁桥台碰撞常用的间隙单元法和非光滑动力学法;何雄君等[10]对地震作用下大跨高墩钢-混结合梁斜拉桥主、引桥梁体之间的碰撞效应进行了分析.
尽管目前对桥梁的碰撞效应进行了一些研究,但对于梁体与台背墙间碰撞研究还不多见,对地震下桥台碰撞失效机理还缺乏了解.为此,文中以一座三跨简支空心板梁桥为例,建立考虑桥台-土相互作用的多跨简支板梁桥碰撞分析模型,分析地震作用下梁体与台背墙间碰撞对桥梁结构的影响以及桥台碰撞失效机理,研究成果可为完善该类桥梁抗震设计提供参考.
1 工程背景与有限元模型
以一典型三跨简支梁桥为例,桥梁整体布置见图1,其跨径布置为3 m×20 m,为先简支后桥面连续结构,桥宽11.75 m;上部结构主梁采用标准跨径20 m的预应力混凝土空心板梁,梁高0.75 m,横桥向由2片边梁和8片中梁并排组成,混凝土强度等级为C50;下部结构为双柱式桥墩、钻孔灌注桩,桩接帽梁式桥台;桥墩盖梁处设置普通板式橡胶支座,桥台台帽处设置四氟滑板橡胶支座连接.
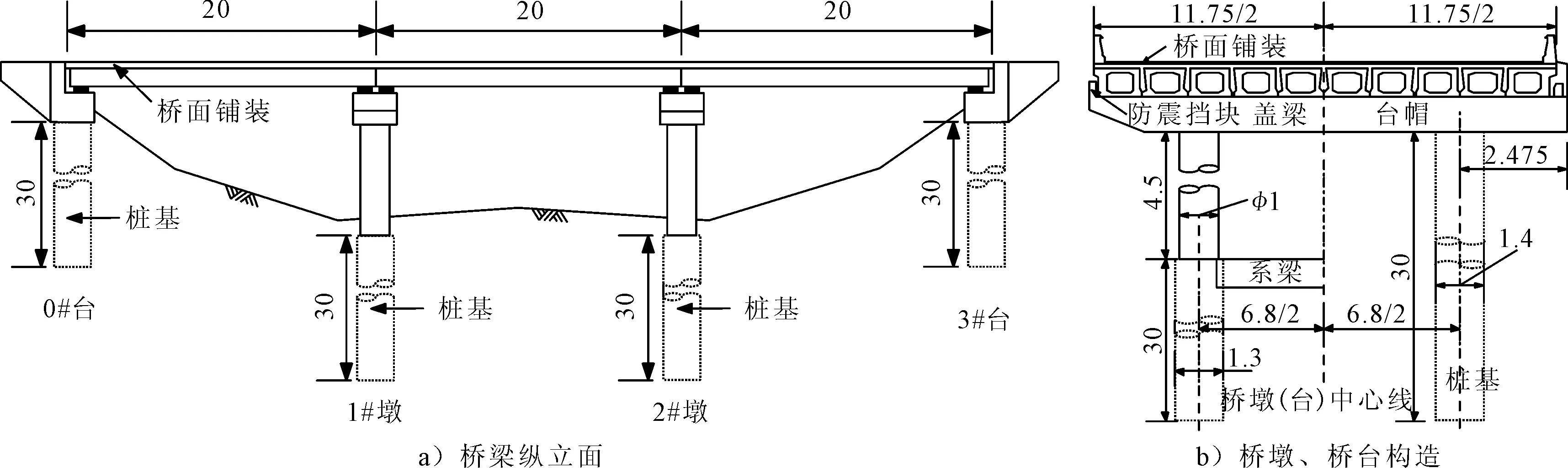
图1 三跨简支梁桥概况(单位:m)
采用开放式地震模拟软件OpenSees建立全桥结构动力分析模型,上部结构、盖梁、台背墙采用弹性梁单元(elastic beam column element)模拟;墩柱、桩基用采纤维梁单元模拟,其中,混凝土的应力-应变本构关系采用Concrete01材料,钢筋的本构关系采用Steel02材料;板式橡胶支座和四氟滑板支座采用理想弹塑性单元模拟,采用双线性模型模拟支座与上部结构之间的滑移效应,根据JTG/T B02-01—2008《公路桥梁抗震设计细则》[11],桥台四氟滑板支座动摩阻系数为0.02,桥墩板式橡胶支座摩阻系数为0.2;采用线性接触单元模拟梁体与桥台的碰撞作用,碰撞刚度K=2.0×106kN/m,伸缩缝初始间隙为d0=6 cm,分析假定桥台背墙不破坏.
采用基于Duncan双曲线模型模拟桥台与台后填土的力-位移关系;采用非线性p-y曲线法建立桥台桩基-土动力相互作用计算模型,其中,非线性p-y弹簧模拟桩周土水平相互作用,非线性t-z弹簧模拟桩侧土竖向摩擦作用,非线性Q-z弹簧模拟桩端土竖向支撑作用.桥梁结构的有限元模型见图2.

图2 桥梁有限元模型图
2 地震动输入
在进行桥梁结构非线性时程地震反应分析时,从美国太平洋地震工程研究中心的强震数据库(PEER)选取20条场地类别接近的实测地震加速度时程(见表1),并将每条地震波的峰值加速度(PGA)调整为0.2g.
3 碰撞对结构地震反应的影响
在建立的有限元模型的基础上,分别考虑以下工况:工况I,不考虑梁体与台背间的碰撞效应,不激活碰撞单元;工况II,考虑梁体与台背间的碰撞效应,激活碰撞单元,初始间隙d0=6 cm.针对工况I和工况II分析模型,在纵桥向分别输入表1所选20条地震波进行非线性时程分析.

表1 所选地震波
3.1 梁体-台背墙碰撞力
图3为工况II模型在20条地震波作用下,上部结构梁体与0号台背墙碰撞力峰值分布.图4为No.1,No.6,No.15地震波作用下对应的碰撞力时程曲线.由图3~4可知,在所选20条地震动作用下梁体与台背墙均发生了碰撞,且产生较大的碰撞力;从碰撞力时程曲线上可以看出,在地震发生过程中梁体与台背墙将发生多次碰撞.
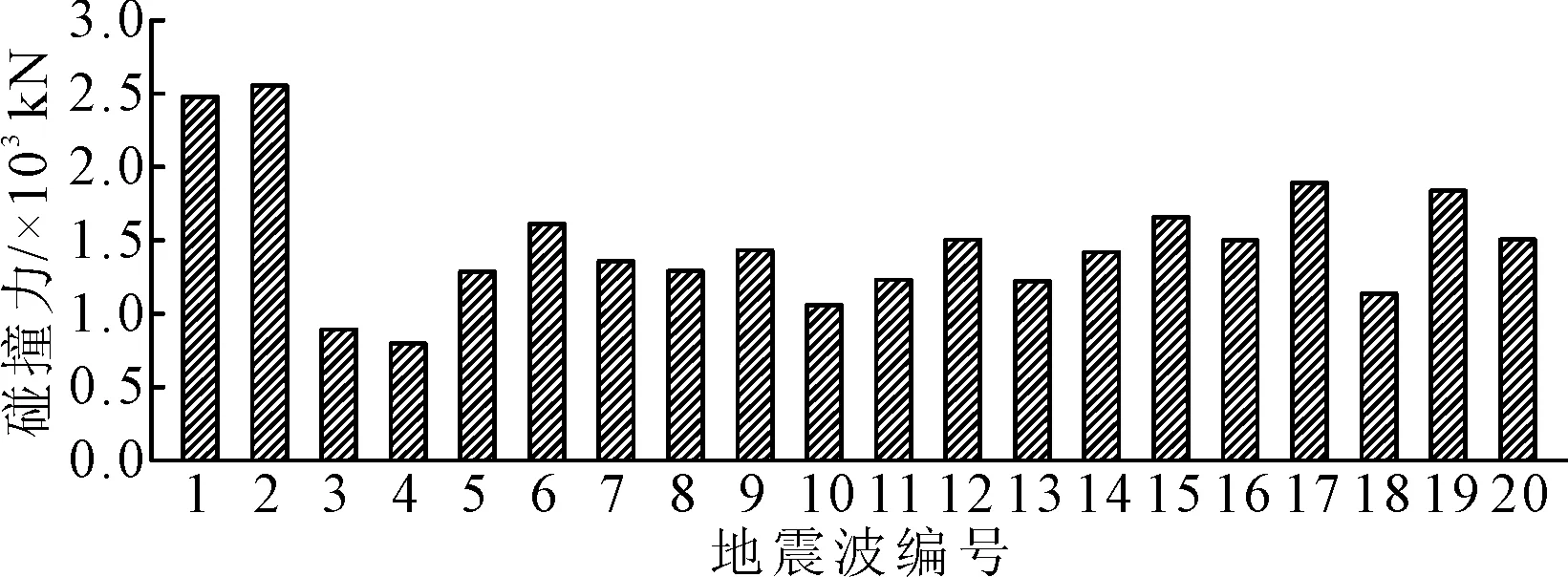
图3 上部结构-桥台碰撞力最大值(工况II)

图4 上部结构-桥台碰撞力时程曲线(工况II)
3.2 主梁位移
图5为在20条地震波作用下,两种工况计算得到的主梁最大位移(绝对值)比较;图6为在No.1,No.6,No.15地震波作用下,两种工况计算得到的主梁纵向位移时程曲线比较.

图5 主梁位移最大值

图6 主梁位移时程曲线
由图5~6可知:考虑上部结构与台背墙的碰撞作用后,由于台背墙对梁体的约束作用,主梁在桥台处不能纵向自由滑动,主梁位移有所下降.台背墙可起到对梁体的限位作用,避免落梁震害的发生,但这是以桥台受到较大的撞击力为代价的,撞击产生的巨大撞击力,对桥台抗震性能不利,台背墙和桩基都有可能发生破坏.
3.3 台背墙底部地震力
图7~8为在20条地震波作用下,工况II计算得到的0号桥台背墙底部产生的弯矩与剪力峰值分布;而工况I,即不考虑碰撞时,台背墙底部地震力很小,其结果未示出.图9为在No.1,No.6,No.15地震波作用下,工况II计算得到的0号台背墙底部的弯矩与剪力时程曲线.

图7 桥台背墙底部弯矩最大值(工况II)

图8 桥台背墙底部剪力最大值(工况II)

图9 桥台背墙底部弯矩、剪力时程曲线(工况II)
由图7~9和图4可知,上部结构梁体与台背墙一旦发生碰撞,台背墙底部将产生很大地震力;且台背墙底部的剪力、弯矩时程曲线与碰撞力的时程曲线形状一致,其峰值数量与峰值时间也基本相同.在地震作用下,桥台背墙是直接承受梁体撞击力的构件,撞击使得台背墙底部产生较大内力,而台背墙底部相对薄弱,这正是历次地震中台背墙破坏较为普遍的原因.
3.4 台后填土变形
图10为在选取的20条地震波作用下,两个工况计算得到的0号台背墙顶部纵向位移最大值比较;图11为在No.1,No.6,No.15地震波作用下,两个工况计算得到的0号台背墙顶部纵向位移时程曲线比较图;图12为在No.1,No.6,No.15地震波加载下,工况I、工况II计算所得0号桥台背墙后填土被动土压力-位移滞回曲线对比图.

图10 桥台背墙顶部位移最大值
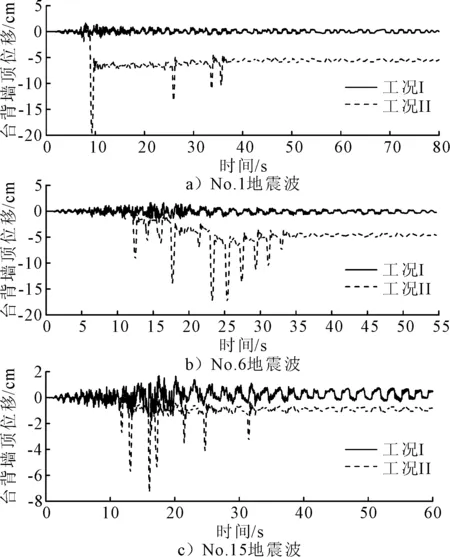
图11 台背墙顶部位移时程曲线

图12 桥台背墙后填土的被动土压力-位移滞回曲线
由图10~12可知,不考虑碰撞时,台背墙纵向位移、台后填土的变形与被动土压力均很小,台后土体基本处在线弹性状态;而如果上部结构梁体与台背墙发生碰撞,巨大的撞击力冲击台背墙,使得台背墙纵向变形增大,并通过台背墙纵向变形将碰撞力一部分传递到台后填土,使得台后填土塑性变形明显增大,台后填土被动土压力-变形滞回曲线非线性特征明显增强.因此,过大的撞击力有可能导致台后土失效,引起桥台倾斜,而且撞击力还将会通过台背传递给桩基础,引起桩基础的震害.
3.5 桥台桩基地震力
对于桥墩墩柱与桩基,由于板式橡胶支座的隔振效果,无论碰撞是否发生,其地震力与变形都不大,篇幅所限,本文不作讨论.以下主要分析碰撞作用对桥台桩基地震力的影响.
图13为在20条地震波作用下,工况II与工况I模型计算所得0号桥台桩基最大地震弯矩、剪力和轴力的比值.由图13可知,碰撞使得桥台桩基弯矩增大了5.1~16.5倍,剪力增大了2.8~10.5倍,轴力增大了1.2~1.8倍;碰撞发生后,撞击力通过台背墙传递给桩基,导致桥台桩基内力显著增大.
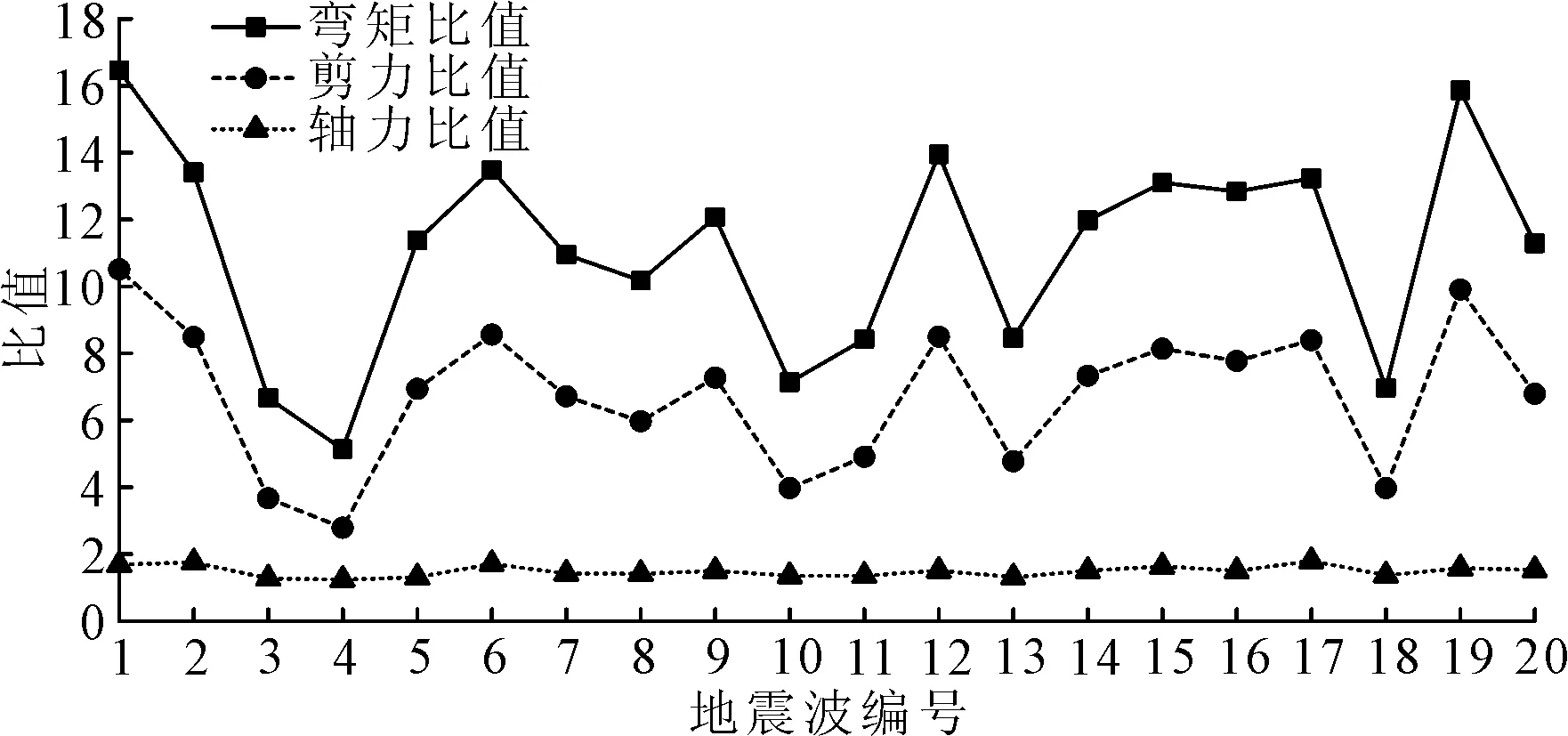
图13 工况II桥台桩基弯矩、剪力、轴力最大值与工况I的比值
图14为在No.1地震波作用下0号桥台桩基的弯矩和剪力包络图;图15为在No.1地震波作用下,0号桥台桩基地震弯矩最大截面处(桩顶下2.0 m)的弯矩时程曲线;图16为在No.1地震波作用下,0号桥台桩基地震剪力最大截面处(桩顶)的剪力时程曲线.由时程图可见,桥台桩基弯矩和剪力时程结果与图4a)的梁体-桥台碰撞力时程结果具有较高的一致性,在碰撞时刻,桥台桩基的地震内力出现峰值,且地震力响应要远大于无碰撞时刻响应.
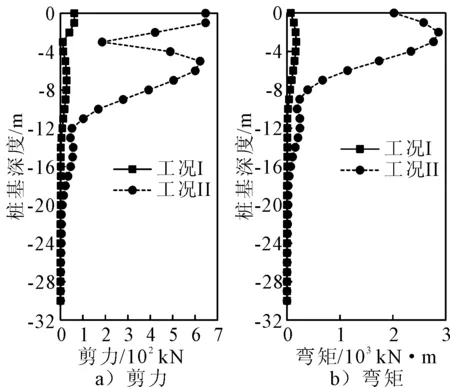
图14 桩基弯矩、剪力包络图(No.1地震波)

图15 桩基深度-2 m截面弯矩时程(No.1地震波)
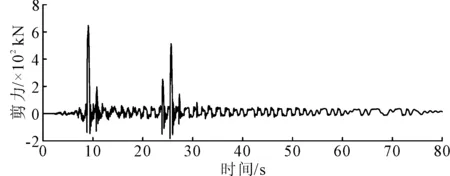
图16 桩顶截面剪力时程(No.1地震波)
4 结 论
1) 地震作用下,不考虑梁体-桥台碰撞时,主梁的纵向位移、残余位移相对较大,桥台桩基地震弯矩、剪力、轴力等很小,台后填土的被动土压力、位移也较小.
2) 地震作用下梁体与台背墙的碰撞作用会有效减小主梁位移和残余位移,即台背墙可起到对梁体的限位作用,但是以桥台受到较大的撞击力为代价.
3) 地震作用下桥台背墙是直接承受梁体撞击力的构件,梁体撞击使得台背墙底部地震弯矩和剪力显著增大,易引起台背墙屈服或剪坏.
4) 地震作用下如果上部结构梁体与台背墙发生碰撞,产生巨大的撞击力,并通过台背墙纵向变形将一部分碰撞力传递到台后填土,使得台后填土塑性变形明显增大,引起台后填土失效、桥台倾斜.
5) 地震作用下梁体对台背墙的撞击力还可传递到桥台基础,使得桥台桩基地震弯矩和剪力显著增大,易引起桥台桩基损伤.

