艏艉型线对参数横摇薄弱性的影响分析
马 坤 梁舒凡 王志宇
(大连理工大学船舶工程学院 大连 116024)
0 引 言
船舶稳性安全是船舶航行安全的重要保障,一直以来受到国际海事组织(IMO)的高度关注.IMO基于大量的事故统计资料和静力学理论,制定了强制性的完整稳性规范,即《2008年国际完整稳性规则》[1].然而许多满足现行完整稳性衡准的船舶在航行时发生了事故,为此IMO有针对性地开展了第二代完整稳性衡准的制定工作.作为第二代完整稳性的五种失效模式之一,参数横摇衡准包含三层,第一层和第二层为薄弱性衡准,第三层为直接计算[2-3].在2019年2月船舶设计与建造分委会(SDC)第6次会议上国际海事组织通过投票初步确定了参数横摇薄弱性衡准规则,下一步的工作除了进行大量的样船计算及验证第一层和第二层的一致性外,还需要研究船型对参数横摇薄弱性的影响,以期在新一代完整稳性规范实施后为船舶设计提供指导.
目前针对船型对参数横摇薄弱性的研究主要集中在船舶主尺度和船型系数等方面,关于船体型线对参数横摇薄弱性影响的研究还很少.因为参数横摇的发生机理与船在波浪中的复原力臂的变化密切相关,而船体型线直接影响到船的复原力臂曲线,因此有必要研究船体型线对参数横摇薄弱性的影响.
文中选取实际航行中发生过参数横摇的C11集装箱船作为母型船,应用船型变换函数调节船体B样条曲面控制点对艏部外飘程度和艉框轮廓线升高高度进行变形,再利用本课题组前期开发的参数横摇薄弱性衡准评估软件对母型船和型线变换后的船进行一、二层薄弱性计算,最后通过对比计算结果得出艏艉型线对参数横摇薄弱性的影响规律.
1 参数横摇薄弱性衡准
参数横摇薄弱性衡准评估分为两层,其中第一层评估通过计算纵向规则波经过船体时,船舶初稳性高的变化幅值来判断是否满足衡准要求,为
(1)
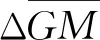
参数横摇薄弱性衡准第二层校核,又分为C1和C2两种不同的计算方法,C1为计算船在给定的16种波浪条件下的失效概率.C2为计算船在北大西洋海浪谱(或船舶航行海域的海浪谱)所给定的海况下,以不同航速,航向角航行时的失效概率.公式[4-6]如下.
(2)
(3)
式中:Wi为权重值;Ci为0或1,当通过计算在某海况下认为容易发生参数横摇则取1否则为0;Vsi为航速,kn;βh、βf为迎浪和随浪.
当满足C1<0.06或C2<0.025的条件时则认为通过第二层校核.具体计算方法见参考文献[7].由于C2方法考虑海况数更多,且需要通过求解横摇运动方程来计算横摇幅值,所以C2计算更为精确,因此本文在进行参数横摇薄弱性衡准第二层校核时仅采用C2方法.
2 生成系列船型
2.1 母型船
选取在实际航行中发生过参数横摇的C11集装箱船为母型船,其主要船型参数见表1,图 1为该船的型线图和艉框轮廓线.由图1a)可知,该船艏部在设计水线附近外飘程度较大,船艉横剖线底部基本为水平线,抬升非常缓慢,由图1b)可知,艉框轮廓线在设计水线附近升高高度较低.以上因素使得C11集装箱船在不同船波相位下水线面面积变化较大,容易发生参数横摇[8].
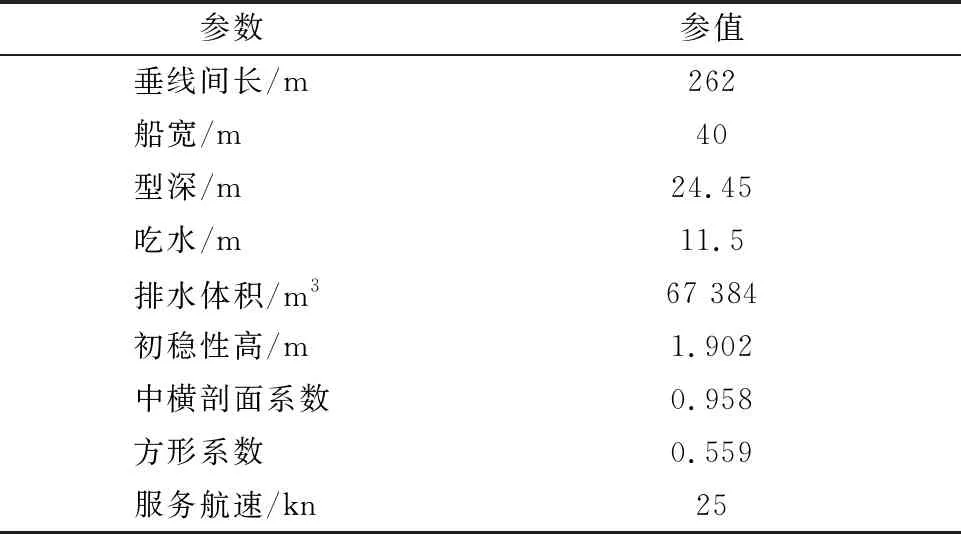
表1 C11集装箱船主要船型参数
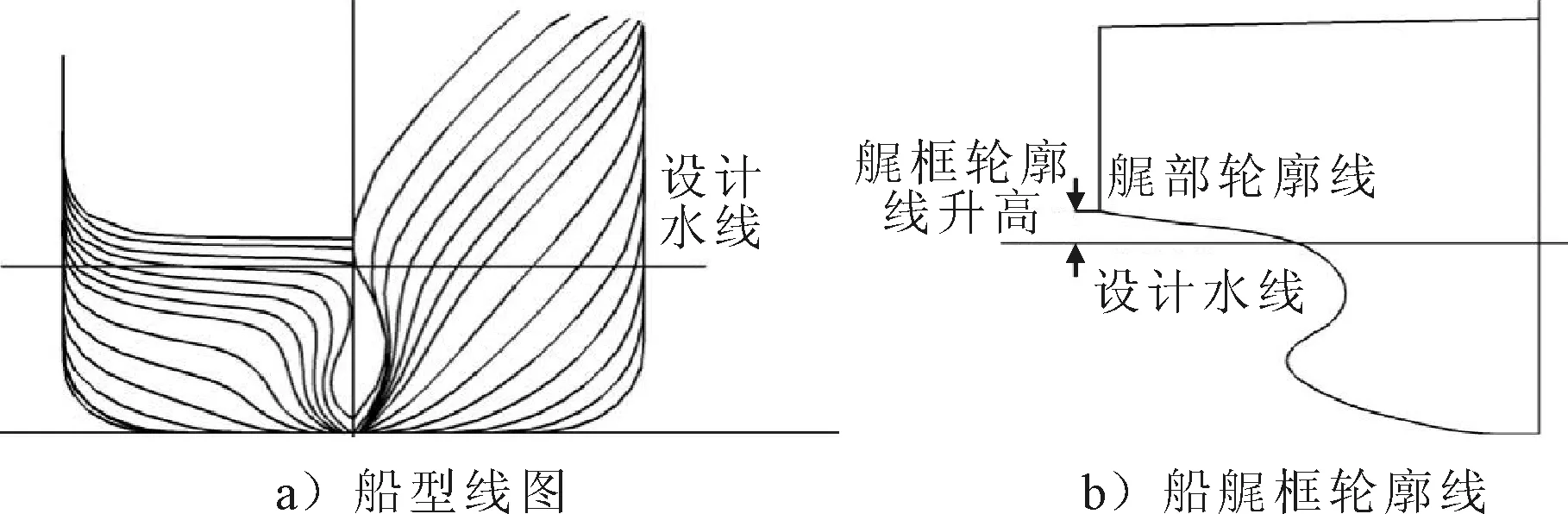
图1 C11集装箱船型线图和船艉框轮廓线
2.2 船型变换方法
船体曲面表达采用B样条曲面.B样条方法具有统一、通用、有效的标准算法,以及强力的配套技术,是目前最广泛流行的形状数学描述方法之一,也是目前关于工业产品几何定义的国际标准,该方法已被广泛应用于船舶、航天、机械制造等众多领域[9-10].k×l次B样条曲面张量积为
(4)
u∈[uk,um+1],v∈[vl,vn+1]
式中:p(u,v)为B样条曲面上的点;di,j为曲面控制点;Ni,k(u),N
调节B样条曲面控制点方法的如下:①由船体型值点反算船体曲面控制点和节点向量;②选定船型变换函数变换船体曲面控制点;③由变换后的船体曲面控制点正算船体曲面型值点.
2.3 船型变换函数
为便于描述船型变换函数,定义坐标系如下,坐标系原点取在中横剖面、基平面和中纵剖面的交点处;X轴沿船长方向指向船艏为正;Y轴沿型深方向指向甲板为正;Z轴沿船宽方向指向右舷为正.分别调节前半体和后半体B样条曲面控制点高度实现对船艏外飘程度和艉框轮廓线升高高度的变换.控制点的高度增量使用拉格朗日插值,插值函数为
(5)
式中:Δy为控制点在Y轴方向的增量;y为控制点在Y轴的坐标;yu、zu为控制点所在剖面内最高控制点的Y轴坐标和Z轴坐标;α为给定系数,α为正时减小设计水线附近及以上船体的外飘程度,增加艉框轮廓线升高高度,α为负时增加设计水线附近及以上船体的外飘程度,降低艉框轮廓线升高高度,|α|越大控制点在Y轴方向变化量越大,型线变化越大;yd为Δy为0时对应的高度值;yc为|Δy|为最大值时对应的高度值,yc满足yu>yc>yd.
2.4 系列船型
应用上述方法,保持船舶主尺度不变,分别对C11集装箱船前半体和后半体进行变形,生成2个系列船型,I系列船型为对前半体进行变形,改变艏部设计水线以上外飘程度后所得的系列船型, 编号从0到4号船艏外飘程度增加,图 2为I系列0号、4号船型线图.II系列船型为对后半体进行变形,改变艉框轮廓线升高高度后所得的系列船型,编号从0到4号艉框轮廓线升高高度逐渐降低,图 4为II系列0号、4号船型线图.2个系列船型的主要船型参数见表 2~3.
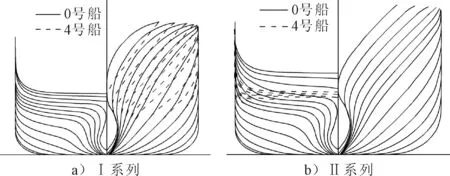
图2 I、II系列0号、4号船型线图
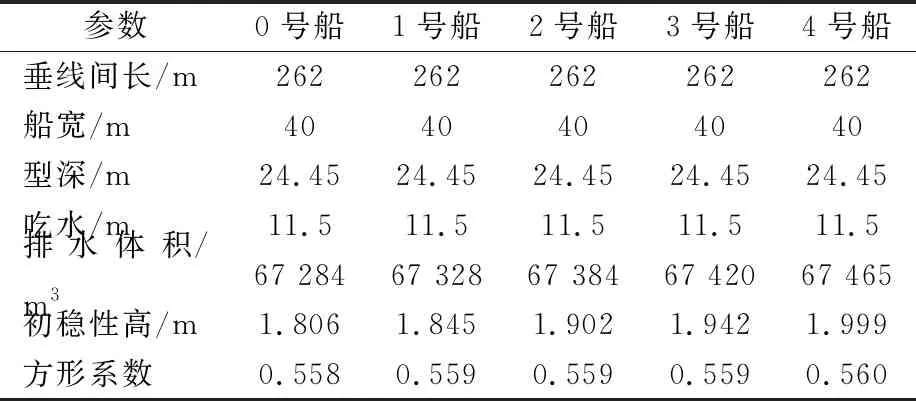
表2 I系列样船主要船型参数
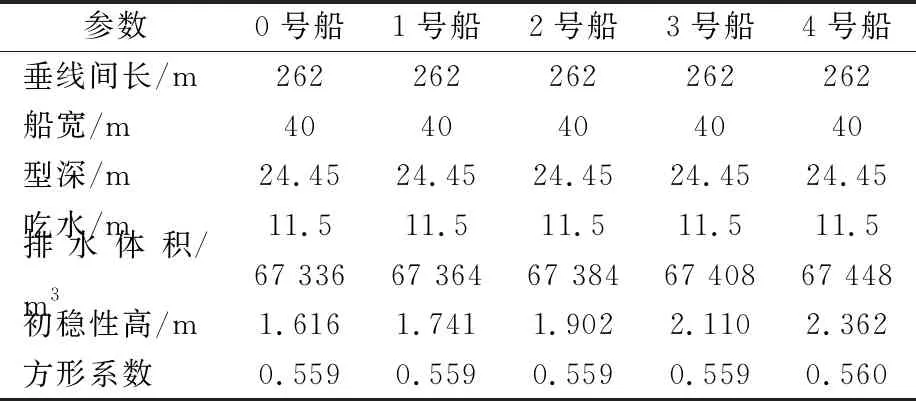
表3 II系列样船主要船型参数
3 艏艉型线对参数横摇薄弱性的影响分析
3.1 船艏外飘对参数横摇薄弱性第一层影响
研究船艏外飘对参数横摇薄弱性第一层校核结果的影响,选取I系列样船为研究对象,采用本课题组前期开发的参数横摇薄弱性校核程序进行计算,在计算时假设同一系列样船重心、吃水等参数相同,且未设置舭龙骨.计算结果见表4.
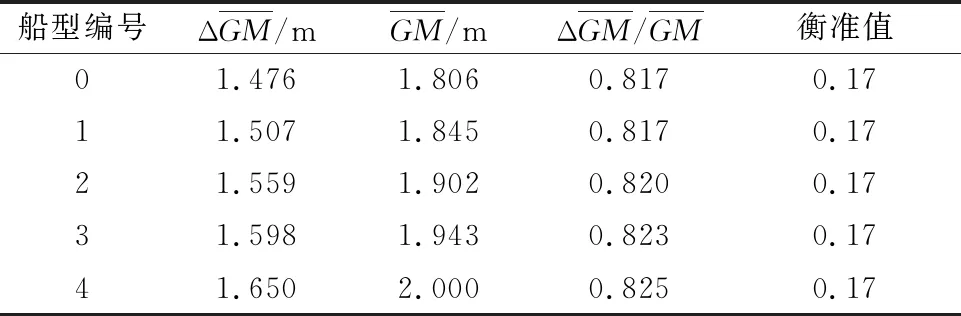
表4 I系列样船第一层计算结果
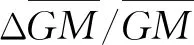
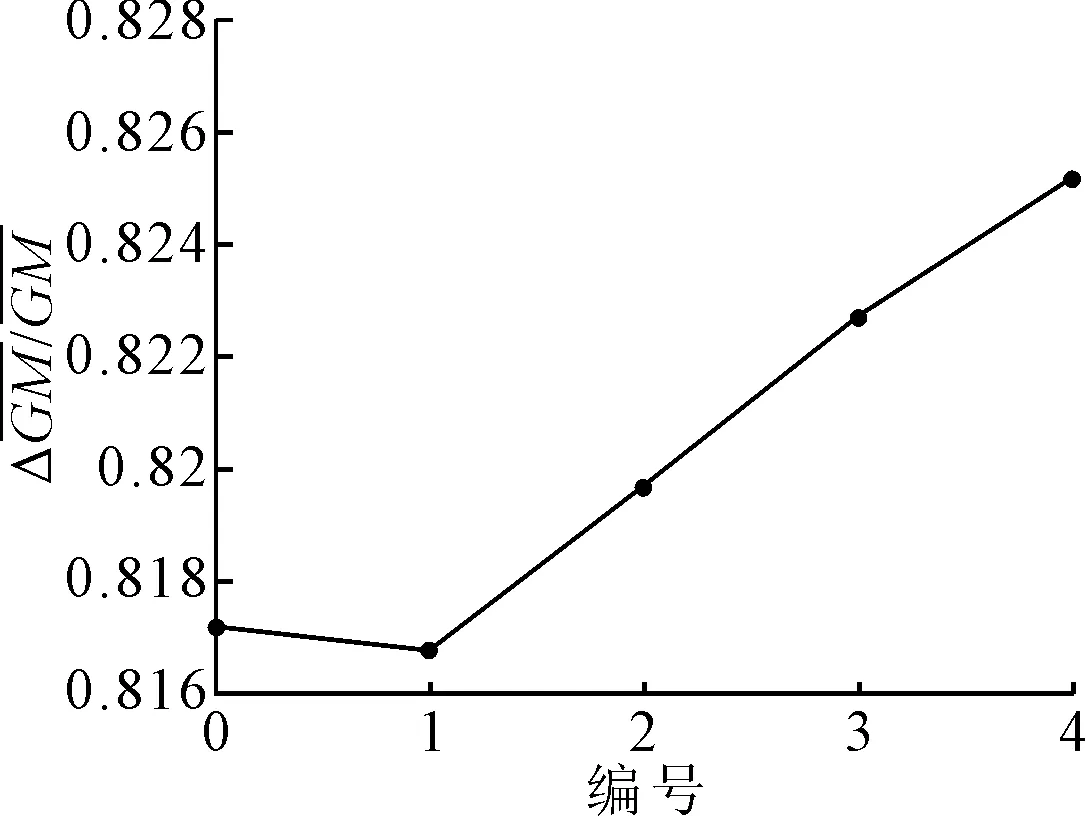
图3 I系列样船第一层计算结果
3.2 艉框轮廓线升高高度对参数横摇薄弱性第一层影响
研究艉框轮廓线升高高度对参数横摇薄弱性第一层校核结果的影响,选取II系列样船为研究对象,采用本课题组前期开发的参数横摇薄弱性校核程序进行计算,在计算时假设同一系列样船重心、吃水等参数相同,且未设置舭龙骨.计算结果见表5.
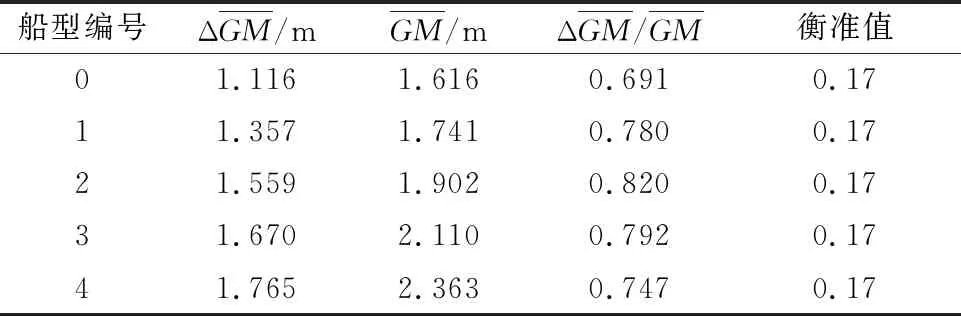
表5 II系列样船第一层计算结果
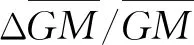
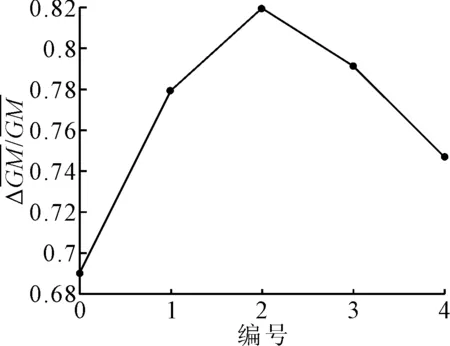
图4 II系列样船第一层计算结果
3.3 船艏外飘对参数横摇薄弱性第二层影响
研究船艏外飘对C11集装箱船参数横摇薄弱性第二层C2计算结果的影响,对I系列0~4号样船进行参数横摇薄弱性第二层校核,采用本课题组前期开发的参数横摇薄弱性校核程序进行计算,在计算时假设系列样船航速、重心、吃水等参数不变,阻尼系数采用池田法计算,自摇周期应用《2008年国际完整稳性规则》中公式计算,横摇幅值采用平均法计算,计算结果见表 6.

表6 I系列样船第二层C2计算结果
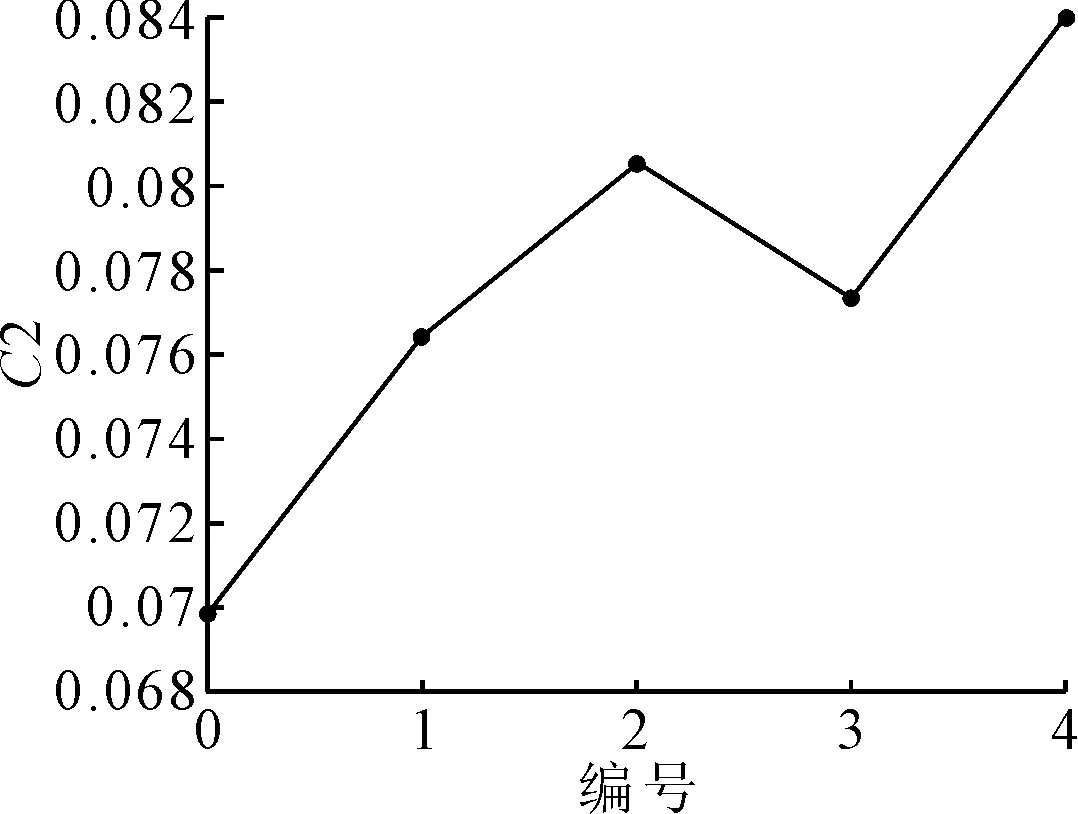
图5 I系列样船第二层C2计算结果
3.4 艉框轮廓线升高高度对参数横摇薄弱性第二层影响
研究艉框轮廓线升高高度对C11集装箱船参数横摇薄弱性第二层C2计算结果的影响,对II系列0~4号样船进行参数横摇薄弱性第二层校核,采用本课题组前期开发的参数横摇薄弱性校核程序进行计算,在计算时假设系列样船航速、重心、吃水等参数不变,阻尼系数采用池田法计算,自摇周期应用《2008年国际完整稳性规则》中公式计算,横摇幅值采用平均法计算,计算结果见表 7.

表7 II系列样船第二层C2计算结果
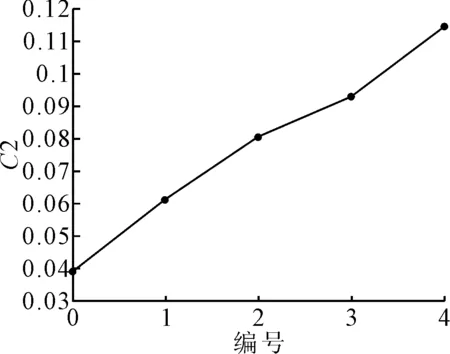
图6 II系列样船第二层C2计算结果
4 结 论
1) 对于参数横摇薄弱性第一层衡准,艏部外飘程度加大或艉框轮廓线升高高度降低,将导致船舶在波浪中初稳性高变化幅值逐渐减小,船舶不容易发生参数横摇.
——福船

