基于可靠度指标的页岩气井水平段套管安全评价*

赵亚婷，樊 恒 ，冯 春，刘沛杭，杨尚谕

(1. 西安石油大学电子工程学院 陕西 西安 710000；2. 中国石油集团石油管工程技术研究院 陕西 西安 710077)

0 引 言

随着油气开采技术的发展与社会需求的提升，常规的油气资源将无法满足未来的能源需求，页岩气作为一种理想的接替能源，逐渐成为各国的重点开采对象。页岩气所处的地质环境较为复杂，地层多以沉积岩层为主，裂缝分布广，井下管柱易受岩石地层滑移发生剪切变形。在页岩气勘探开发中，水平井钻井技术及压裂技术是关键技术，开采过程需开展多级压裂，长期的高强度压裂施工造成了一定套损隐患[1-2]。同时，页岩储层还具有易水化膨胀、易破碎、井壁不稳定、完井困难等特点，进一步导致套管损坏频发[3]。因此，结合页岩气井的服役特点分析其管柱的强度性能及应变特点，建立页岩气管柱的安全评价模型具有重要的工程意义。

相关研究表明，页岩气井套变主要来源于水力压裂时流体压力传递至地层发生剪切滑移，井下水平段水泥环对应力的吸收量与管柱自身的抗形变量之和不足以抵抗地层的双向应力时，管柱则发生断裂。在威远地区的页岩气井现场统计数据中发现，经过调整壁厚来提高套管抗挤安全系数后的套管在地层滑移的影响下仍无法避免损坏[4-6]。此外，在固井质量越好的井段，由于套管与地层耦合良好直接提高了地层剪切力向套管的传递。可见，地层剪切滑移量是页岩气井下管柱应变评价的重要参量。

目前国内外对套管的可靠性校核，是针对套管所受外载的工况，选用确定的校核准则进行安全评价，包括最大拉应力准则、最大剪应力准则、最大Mises应力准则等确定性方法[7-9]。然而，运用确定性的方法进行安全评价，不能定量分析套管所受荷载及其强度的不确定性，也无法定量描述某一段套管有可能出现的失效概率[10-12]。对此，本文结合结构可靠度设计及评价理论，建立一种基于可靠度指标的页岩气井管柱可靠度安全评价模型，从强度及应变两个角度，探讨页岩气井水平段各不确定性因素对管柱可靠度指标的影响规律，为页岩气井管柱的设计及套变安全防治提供技术支撑，对实际工程提供更好的指导作用。

1 页岩气井水平段套管可靠性评价模型

页岩气水平井管柱长期受到储层天然裂缝及地层滑移的影响，多级压裂施工更进一步升级了外载对井筒结构的威胁。对此，以页岩气水平井套管在地层滑移作用下最易发生的剪切变形为背景，从强度与应变两方面对其进行可靠性评价，分析水平段套管的强度-应力分布规律及地层-水泥环-套管之间的应变位移关系，建立了页岩气井水平段套管的可靠性评价模型，如图1所示。

根据结构可靠性理论，在一般情况下，总可以将影响结构可靠性的因素归纳为两个综合量，即结构或结构构件的荷载效应S和强度R。

Z=g(R,S)=R-S

(1)

式中，Z为结构功能函数。实际工程中的荷载效应S和强度R均为随机变量，因此Z也是一个随机变量。对此，总可能出现下列3种情况：Z>0，结构可靠；Z<0，结构失效；Z=0，结构处于极限状态。下式称为结构极限状态方程。

注：图中为描述方便，采用统一参数Xi为功能函数基本变量。图1 页岩气井水平段套管可靠性评价框图

Z=R-S

(2)

根据可靠度指标的定义，用参数μZ、σZ分别表示状态值Z的平均值与标准差。则可靠度指标β为：

(3)

由于μZ、σZ精确求解比较困难，故采用功能函数Z的解析表达式进行求解。假设S*、R*为S、R在验算点P的值。将Z在验算点处进行一次线性展开，则

(4)

假定功能函数Z的表达式中所有参数均符合正态分布，此时可靠度指标β可表述如下：

(5)

定义荷载和强度敏感度系数分别如下：

(6)

(7)

则验算点的值可以描述为

S*=μS(1+βδSαS)

(8)

R*=μR(1+βδRαR)

(9)

式中，μs、σs和μR、σR分别为套管荷载S和强度R的平均值和标准差，δS=σS/μS、δR=σR/μR为套管荷载和强度的变异系数。

由于验算点P未知，一般假设初始验算点为套管强度与荷载的均值处(μR、μS)，利用图1的方法进行迭代计算，直至前后两次的计算结果误差满足给定的容许值ε=10-3，即可认为最后一次的迭代计算结果为该处可靠度指标。

2 页岩气井水平段套管强度评价

页岩气井水平段分布较长，不同井段对应的储层性质差异大，多级注水施工带来的复杂荷载使水平段套管长期处在复杂极端的力学环境中，套变问题严峻[13-15]。西南地区页岩气井在2014～2018年期间水平段套管变形日趋严重，如图2所示。2018年套变井比例接近50%。

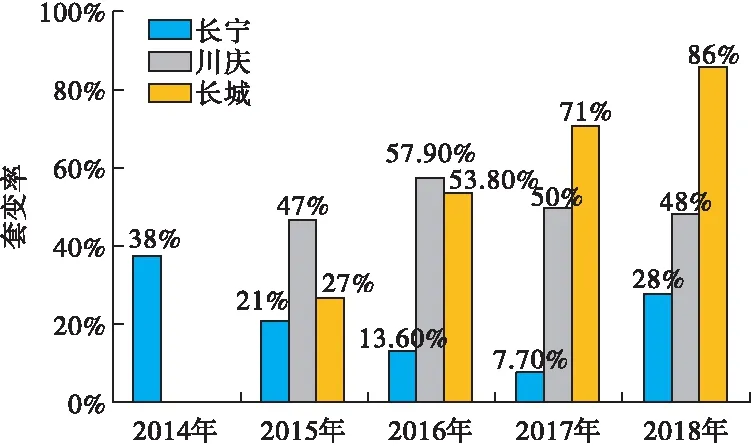
图2 川南页岩气区块2014～2018年套变发生比例

长宁、威远区块套管变形平均40%，威远长城风险区套变比例高达86%。以威远-长宁为例，在水平段A点附近变形比例为62.5%，中间段变形占比37.5%，B点附近未出现变形点。

与常规油气井(直井)相比，页岩气井水平段套管的强度性能更易受弯曲应力及压裂施工带来的地层剪切应力的影响，对其进行强度评价时，主要针对固井后服役过程中水平段套管所受到的外挤应力S与其自身强度承受力R建立功能函数，极限状态方程表示为：

Z=g(R,S)=R-S

(10)

式中，R泛指套管材料强度设计值，此处主要指抗外挤强度；S泛指套管所受荷载作用设计值。

由于在对套管进行评估时，套管已服役，故将套管抗挤强度按照塑性抗挤强度进行计算，根据SY/T 5724规范中的计算方法，采用的抗挤强度R计算公式为(式(11)～(14)分别为塑性抗挤强度、屈服抗挤强度、过渡抗挤强度、弹性抗挤强度)：

(11)

(12)

(13)

(14)

式中，Yp为套管屈服强度， MPa；(a/δ)为塑性挤毁与过渡挤毁交点的径厚比；a为套管外径，mm；δ为套管壁厚，mm；其余参量含义及计算见SY/T 5724规范。

由于地处天然裂缝带，页岩气井水平段套管的外部荷载主要来源于压裂施工后裂缝扩张引起的流体压力积聚，当地层滑移带来的剪切应力大于缝隙压力与套管-水泥环临界抗力之和时，套管则会发生剪切滑移变形。结合文献[13]建立的地层-裂缝-套管系统受力模型，本文主要探究外部剪切挤压荷载对水平段套管的作用。对于投入生产阶段的套管，此处考虑固井完成后地层裂缝被压裂液充分撑开后缝隙间岩石无摩擦的情况，当前套管-水泥环结构受到的外部剪切荷载S[13]为：

(15)

(16)

式中，σH、σh分别为最大、最小水平主应力，MPa；Af为天然裂缝面的面积；Ac为井筒与裂缝截面处水泥环及套管所围的圆环面积；R为井筒半径；r1为套管内径；α和θ分别对应裂缝逼近角和井筒逼近角。

3 页岩气井水平段套管应变评价

多项研究表明，页岩储层中的天然裂缝、多级压裂施工、地层滑移是导致页岩气井套管变形的主要原因[16]，对此，相继有学者从套管强度与应力场分布等角度探索套损机理并对套变规律进行分析与评价。其中发现，页岩气井水平段套变以屈服、剪切破坏为主，地层-水泥环-套管组成的井筒结构在外部荷载下发生的形变多为塑性形变，对于特定的复杂地层荷载，要从增强对地应力的吸收能力入手，提高固井水泥的“顺从性”[17-21]。相反，增强套管强度性能及固井质量无法从根本上缓解套变问题。因此，研究页岩气水平井的套变除从强度-应力的角度外，还应结合套管的应变特点综合分析地层应力向井筒结构的传递作用。

页岩储层中的裂缝在压裂后会聚积流体，此时产生的地层剪切应力通过固井水泥环并传递至套管上，水平段的套管在上下两侧非对称应力的共同作用下发生剪切变形。作为井筒结构的重要组成部分，水泥环连接了地层与套管，在地层滑移产生位移后，套管外侧的水泥环将吸收部分应力削弱套管外载。对此建立页岩气井水平段套管应变功能函数，极限状态方程为：

Z=g(Ld,Ls,Lt)=Ld-(Ls+Lt)

(17)

式中，Ld、Ls、Lt分别为地层滑移量、水泥环吸收形变量、套管形变量。根据极限状态方程可发现，在地层滑移量一定的情况下，水泥环对应力的吸收量越大，套管形变量则越小。

此处，地层滑移量Ld将根据现场实际测量数据所得的拟合曲线选取其平均值。

近年来，伴随经济的快速发展，中国城镇化进程不断加快。2011年，中国城镇人口超过乡村人口，1978-2017年，城镇常住人口从1.7亿人增加到8.1亿人，城镇化率从17.9%提升到58.5%。河南作为一个人口大省，到2017年年底，全省总人口达到10 852.85万，城镇化率首次突破50%。在城镇化的发展过程中，城乡融合逐渐深入，但乡村空心化、公共服务滞后、发展动力不足等问题并未得到有效解决，传统的乡村治理体系面临严峻的挑战，亟须建立与城镇化相适应的新的乡村治理体系。

套变量Lt的计算模型选取文献[13]建立的复合型裂缝模型，由于含裂缝地层产生的滑移剪力成因复杂，水平段套管在此应力作用下产生的形变量近似等于地层裂缝在切向的滑移量，计算公式为：

(18)

式中，υ为岩石泊松比；a为地层裂缝长度的一半，m；τ为套管受到的剪切应力，MPa；E为岩石弹性模量；k′为k点在X轴上的坐标值(此处可理解为验算点在X轴的坐标值)，m。

图3为页岩气井水平段剪切变形示意图，从井筒截面图可看出，水泥环在井筒结构中主要起到连接套管与地层的作用。当地层应力作用在井筒结构上时，固井水泥环将“吸收”部分应力缓解套管变形[22-23]。对此，相关学者提出通过增加水泥环厚度或采用高柔性(弹性)材料来增加水泥环对地层应力的抵抗能力。本文将根据文献[24]中建立的力学模型并结合拉梅公式计算页岩气井水平段水泥环的位移量(吸收量)：

(19)

式中，μi(i=1～3)依次为套管、水泥环、地层的泊松比；Ei(i=1～3)依次为套管、水泥环、地层的弹性模量，GPa；此处只计算水泥环的形变量，根据文献[24]，此时需取i=2，则对应的第一界面(水泥环-套管)应力p2与第二界面(地层-水泥环)应力p3分别为：

(20)

(21)

式中，k1～k8为与套管、水泥环及地层相关的中间参数，其计算及相关含义见文献[24]。

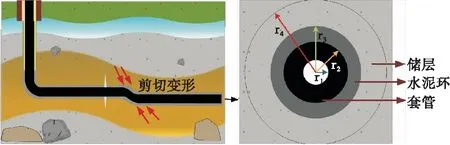
注：r1～r4分别对应套管内径、套管外径(水泥环内径)、水泥环外径(地层内径)、地层外径。图3 页岩气水平井剪切变形(左)、井筒截面(右)示意图

4 应用实例

以页岩气水平井为例，该井的地面海拔145.42 m，总井深3 932 m，最大最小水平主应力分别为30 MPa与25 MPa，该井的井筒相关参数信息见表1，套管强度及应变评价相关设计参数见表2。根据上文建立的评价模型，按图1的流程分别计算套管强度及应变的可靠度指标，对于不符合正态分布的基本参数，结合概率论与数理统计的方法对其进行当量正态化，获得当量正态均值及方差后带入迭代过程，即可求得可靠度指标。

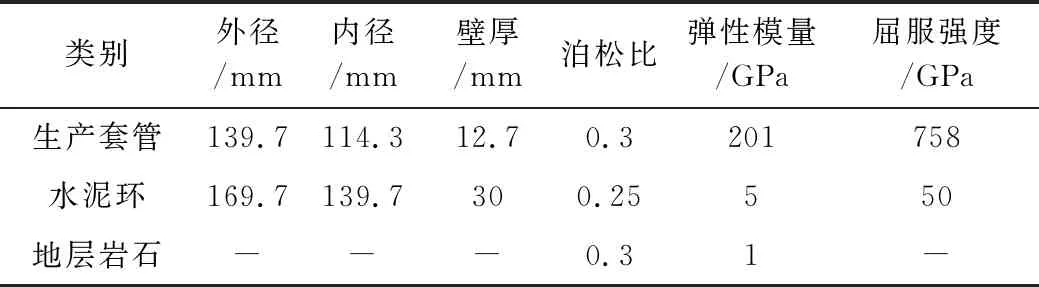
表1 页岩气水平井井筒参数表

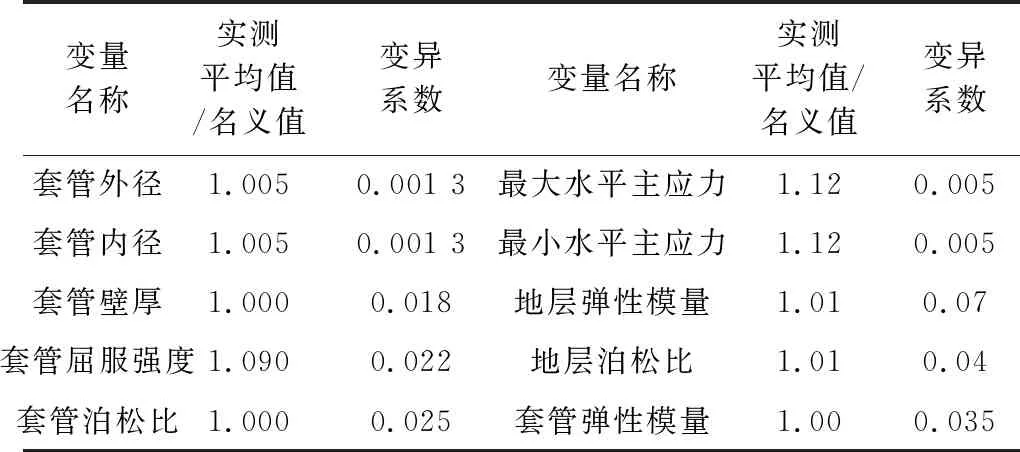
表2 套管强度/应变评价设计参数表

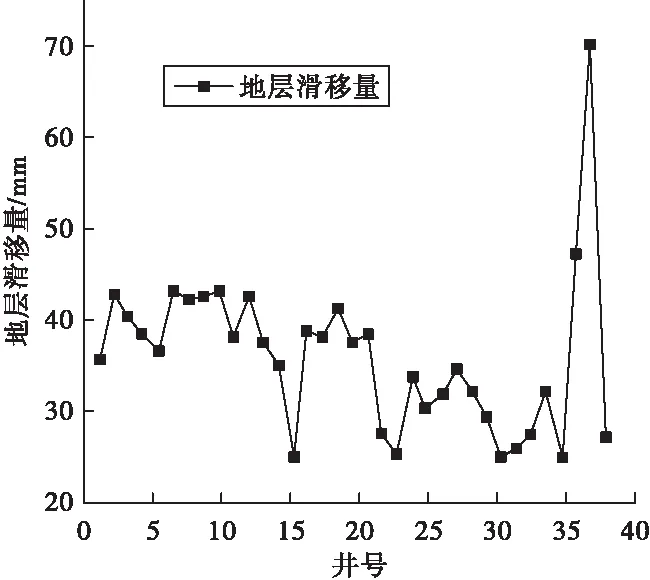
图4 套变尺寸统计曲线

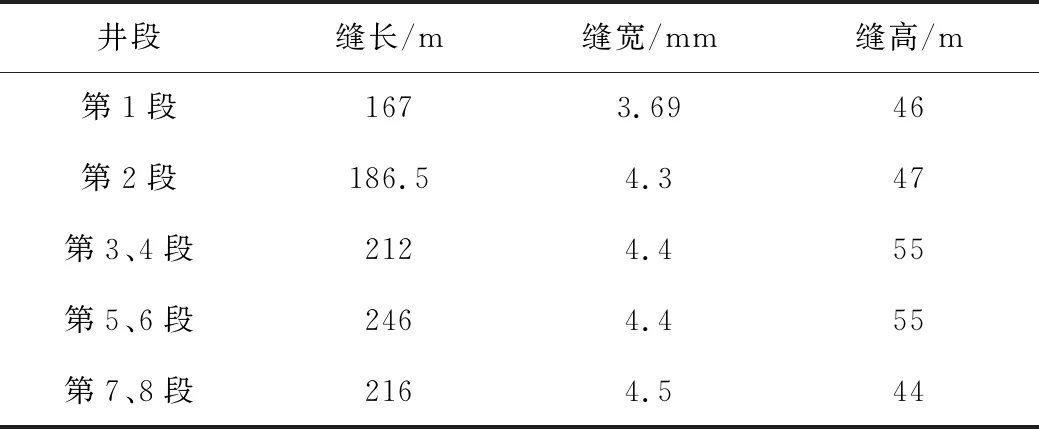
表3 页岩气井水平段裂缝信息

分别选取功能函数中各变量的平均值为初始验算点进行计算，水平井不同位置套管的抗挤强度的计算、套管内压、地应力等中间变量依据SY/T 5724求取。经迭代计算后，最终求得该水平井第1段至第8段套管强度评价可靠度指标均为10.56。应变评价的可靠度指标见表4。

表4 可靠度指标计算结果

从表4的计算结果可看出，与强度评价相比，页岩气井水平段套管的应变评价可有效计算不同井段套管的可靠度指标，从形变位移的角度分析了地层-水泥环-套管结构的可靠性，实现对水平段套管服役状况的定量评价。

5 结 论

1)结合页岩气水平井套损特点及页岩储层的滑移特点，基于可靠度指标建立了水平段套管安全评价模型，从强度与应变两方面选取相关变量并建立了结构功能函数。

2)在强度评价中，不同井段套管的抗挤强度因管柱规格一致而取定值，外挤荷载则考虑了储层天然裂缝及其与井筒逼近角等因素，在建立的评价模型下迭代计算得出了水平段套管的可靠度指标，实现了套管强度与荷载的定量评价。

3)在应变评价中，根据微地震监测数据与软件模拟发现裂缝分布对不同井段套管形变量影响显著，借助套变尺寸获取了地层滑移量统计数据，经迭代计算得出了水平段套管的可靠度指标，从形变位移的角度定量评价了地层-水泥环-套管结构的可靠性。

4)通过对比套管强度评价与应变评价结果可发现，应变评价能更好地反映水平段不同位置套管的可靠性，本文建立的评价模型对实际工程具有一定的指导意义。