基于分布式光纤传感的盾构隧道沉降监测方法研究
武 建,王 涛,李 波,曾强东,姚彦东,2
(1.华设集团股份有限公司水下隧道智能设计、建造与养护技术与装备交通运输行业研发中心,南京 210014;2.河海大学土木与交通学院,南京 210098)
随着城市现代化的进程,地铁轨道交通呈现快速发展的趋势,以满足城市发展的需要,其中,盾构隧道是地铁的主要维护结构.由于临近基坑开挖[1-2]、地表的加载卸载[3-4]、近距离隧道的穿越[5-7]及地质变化等因素,容易引起土体的附加应力,不利于隧道结构的沉降稳定,过大的沉降还会导致安全问题.因此,相关学者提出了盾构隧道结构健康监测[8-9],并进一步进行预测预警研究,保障盾构隧道运营安全.
针对盾构隧道沉降监测,现阶段的相关技术主要有以下几类:①精密水准测量技术,已在隧道建设中得到大量运用,如宁波轨道交通3号线等[10-11],测量精度高,但作业效率低,强度大,难以实现自动化;②全站仪,如梅文胜等[12-13]利用全站仪监测隧道的整体沉降并建立自动化系统,测量精度高,但仪器价格昂贵无法大面积布设;③静力水准仪,如孙泽信等[14]采用静力水准仪监测隧道运营期沉降,但该系统存在水头损失等长期性能问题;④三维激光扫描技术,如李宗平等[15-17]应用三维激光扫描技术进行点云拼接监测隧道沉降,该方法自动化程度高,高效快速,但精度不足;⑤电水平尺监测技术,如赵太东[18]应用这一技术监测地铁的运营沉降,该方法安装简单,数据自动传输,但价格较为昂贵,难以大范围布设.总而言之,既有技术难以兼顾低成本大规模布设和准确测量.
分布式光纤传感技术具有传感距离大、稳定性好、耐久性强等优势,在隧道结构监测方面前景广阔.涂传圣[19]初步研究了分布式光纤传感技术在盾构隧道不均匀沉降方面的应用,但只能定性而不能定量判断隧道沉降.基于梁变形理论[20]和分布式光纤传感技术[21],本文提出了隧道沉降的分布式监测方法,并通过缩尺模型进行了试验验证.
1 分布式光纤传感技术
1.1 传感原理
布里渊散射是光在光纤内传输引起的一种散射现象.通过研究发现,布里渊散射散射光的中心频率变化与光纤(产生散射位置的)的应变和温度成线性相关,因此,可用来进行应变或温度测量.
基于受激布里渊散射机理的测量系统称为BOTDA(Brillouin Optical Time Domain Analysis),其基本原理如图1所示.典型系统如日本光纳株式会社(Neubrex Co.Ltd.,)的NBX-6050,其应变测量精度为7.5με,温度测量精度为0.75℃,空间分辨率为10 cm,数据采样间隔5 cm,本文的研究基于此展开.
1.2 应变传感性能
采用悬臂梁静力加载的方式(图2),对分布式光纤应变传感性能进行了验证.采用环氧树脂将光纤黏贴在悬臂梁上表面,为了对比,在悬臂梁上表面跨中位置还布设了一支电阻应变片.通过在自由端悬挂重物的方式对悬臂梁实施加载,依据荷载大小不同,分为7个工况,即工况1~工况7.
应变测量结果如图3所示,结果表明:测量获得的应变分布与理论分布趋势一致;同时,跨中位置的光纤应变测量值与应变片应变测量值接近,误差范围为-5~13με,误差比理想状态下大,主要原因是BOTDA技术对于空间分辨率内复杂应变的测量精度会有所下降.

图1 BOTDA技术的基本原理Fig.1 The basic principles of BOTDA technology

图2 试验装置Fig.2 Experimental device
2 盾构隧道沉降变形的监测理论

图3 应变结果Fig.3 Strain results
目前,盾构隧道纵向性能分析时常采用等效刚度模型和梁-弹簧模型,其中等效刚度模型概念明确、便于解析推导.此外,基于应变的盾构隧道沉降计算方法主要有单位荷载法和共轭梁法,其中,共轭梁法无须知道隧道的刚度参数,可以直接得到隧道沉降的整体分布,而单位荷载法需逐点计算.因此,本文采用了纵向等效刚度模型,并基于共轭梁法开展隧道沉降监测方法研究,其计算模型如图4所示.

图4 隧道沉降计算模型Fig.4 Tunnel settlement calculation model
为了简化,本文将监测区域内沉降槽两端(即应变基本不变化的位置)视为简化梁的支座,两端沉降基本为零,故简化为简支支座.沉降槽中间的地基反力视为外部荷载加于模型结构上,即将复杂的连续梁问题转化成单跨梁问题.
根据共轭梁方法的原理,共轭梁上的荷载分布p是实际梁上的曲率分布,即

式中:x是传感器到梁左端部的距离;y是传感器到梁中性轴位置的距离;ε(x)是传感器在梁x位置处测量的应变;p(x)是施加在共轭梁x位置处的荷载.
实际梁的挠度分布D就是共轭梁的弯矩分布M,为了计算弯矩分布M,需要首先计算左端支座反力Q0,

式中:L是梁的长度;dx是x的微分量.
进一步地,共轭梁的弯矩分布M可表达为

式中:M(x)是共轭梁x位置处的弯矩;t是计算荷载p(t)产生的弯矩时,新设的位置变量,与x含义相同.
上式计算的共轭梁弯矩分布在数值上即为实梁的沉降分布.
3 室内模型试验研究
3.1 试验概况
本试验采用一根长3.8 m左右的塑料管模拟隧道,其外径为20 mm,壁厚为1 mm.采用玻璃制作一个尺寸为4 m×0.8 m×0.5 m的容器,里面堆细砂,高度为0.6 m,模拟隧道周边的土体.塑料管埋设在砂土中间,其表面沿纵向轴线粘贴一根分布式光纤传感器,两端通过光纤引线连接数据采集设备NBX-6050.为了进行比较,在塑料管中间及其两边各0.5 m位置布设了三个位移计,位移计的测量精度为0.01 mm,具体如图5所示.
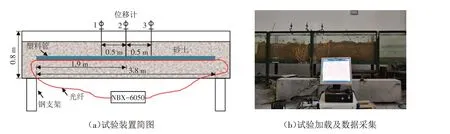
图5 室内隧道模型试验装置Fig.5 Indoor tunnel model test facility
为了使隧道产生位移,采用在塑料管中间位置上部对砂土加压力,使土层挤压,从而使塑料管产生沉降.加压区域在中间位置左右各0.2 m范围内,以位移计2的数值作为加压参考值;按照沉降大小不一样,分为5个工况,即工况1~工况5.
3.2 试验结果
3.2.1 应变结果 图6显示了不同工况下的应变测量结果,从结果中可以发现:以加压位置为中心,应变对称分布;加压区域的应变变化最为显著,其中加压下方出现应变正号峰值,在左右两边各约0.3 m的位置出现应变负号峰值;在1.15~2.9 m范围内,应变分布与5跨连续梁在中间跨加载情况下的应变分布类似,而1.15~2.9 m范围以外,应变变化很小,因此,取沉降的影响范围是1.15~2.9 m.
3.2.2 沉降结果 通过对应变分布式情况的分析,取1.15 m处和2.9 m处分别为隧道简化模型(简支梁)的两端支座,其沉降为零,并将应变分布代入公式(1)~(3)计算沉降分布,结果如图7所示.结果表明:计算沉降与理论分析的沉降横向分布形状一致;在工况1和工况2中,部分区域出现了向上的位移(即反拱).

图6 应变测量结果Fig.6 Strain measurement results
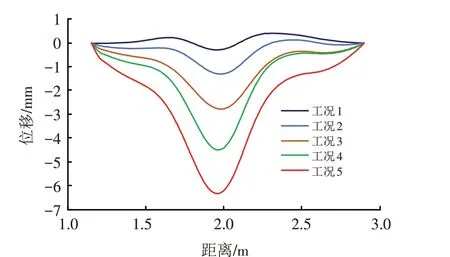
图7 沉降分布计算结果Fig.7 Settlement distribution calculation results

图8 沉降结果比较Fig.8 Comparison of settlement results
提取与位移计布设位置相同的沉降计算值,并与位移计测量值进行比较,结果如图8所示.结果表明,光纤测量获得的沉降与位移计测量的沉降数值接近,发展趋势一致.但是,两者之间也存在差异,其中最大差异不超过0.5 mm.分析误差产生主要原因,包含:①简化模型与实际模型存在差异;②在局部复杂应变分布下,BOTDA应变测量精度下降.在实际监测中,沉降影响的范围较大(一般在几米或几十米),在BOTDA的空间分辨率范围内光纤的应变变化梯度不会太大,可以保证应变测量精度,即可以提升沉降监测精度.
4 结论与建议
本文通过静载试验,验证了分布式光纤传感技术应变传感性能,并基于共轭梁理论和分布式应变测量,提出了盾构隧道沉降监测方法,最后通过模型试验验证了其有效性,得到了以下结论:
1)分布式光纤传感技术具有优良的应变传感性能,可大范围布设、测量精度高,适用于盾构隧道结构这类长距离分布结构的分布式监测;
2)结合共轭梁方法和分布式应变测量,可以建立盾构隧道沉降监测的理论和方法,模型试验验证了其优良的测量效果;
3)在复杂应变分布下,可进一步提升BOTDA技术的应变测量精度,以满足某些特殊情况下的盾构隧道沉降高精度监测需求.

