智能车辆路径跟踪与稳定性的模型预测控制

邹旭东，贾志强，张丽霞

(青岛理工大学 机械与汽车工程学院，山东 青岛 266520)

路径跟踪是智能车辆运动控制的核心问题之一，如何在跟踪目标路径的同时保持车辆的行驶稳定性也是车辆控制领域的研究热点[1]，国内外许多专家学者都对此展开了研究。邹凯等[2]为了提高整车模型精度，将轮胎模型Pacejka-98在每个控制周期都进行线性化，基于车辆的线性时变模型，设计了带有控制量和控制增量等约束的模型预测控制器(MPC)，跟踪精度较高，但是没有考虑跟踪过程中车辆的稳定性问题。陈特等[3]设计了一种兼顾路径跟踪与稳定性控制的滑模控制器，并提出一种轮胎力优化分配方案，在良好路面上实现了期望轨迹跟踪，但是未对冰雪路面上的稳定性控制进行研究。孙跃东等[4]将汽车横摆角速度名义值与实际值之差作为控制器的参考量，设计了以模糊比例积分微分(PID)算法为基础的车身电子稳定系统(ESP)控制器，对汽车高速行驶在干燥沥青路面上的工况进行联合仿真分析，达到了较好的稳定性控制效果。王艺等[5]通过对车辆三自由度模型进行线性化，并加入控制量和控制增量约束，设计了一种MPC路径跟踪控制器，并考虑质心侧偏角等约束，在中低速下实现了较好的路径跟踪效果。上述研究中均未对车辆在冰雪路面上跟踪期望路径的工况展开研究，这显然与我国北方冬季经常出现冰雪路面的实际情况不相符[6]。

本文中基于线性时变模型，设计充分考虑冰雪路面上车辆行驶稳定性的MPC路径跟踪控制器，考虑到车辆在附着系数较小的路面上行驶时易发生侧滑的情况，在控制前轮转角进行路径跟踪的同时引入附加横摆力偶矩来矫正车身姿态，并根据一定的分配逻辑分别计算4个车轮上的制动力矩输出给车辆模型，以保证一定的路径跟踪精度，同时充分保障车辆的稳定性和安全性。

1 车辆模型

1.1 车辆二自由度模型

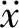
根据牛顿第二定律，二自由度模型车辆动力学方程为

(1)

(2)

xoy—车辆坐标系；XOY—惯性坐标系；车辆在x轴方向的速度；车辆在y轴方向的速度；车辆横摆角速度；β—车辆质心侧偏角；Fcf、Fcr—前、后轮胎的侧向力；αf、αr—前、后轮胎的侧偏角；δf—前轮转角；a、b—车辆质心到前、后轴的距离。图1 车辆二自由度模型

1.2 轮胎模型

轮胎作为车辆与路面接触的唯一介质，结构复杂并有高度非线性动力学性能，因此选择准确且便于应用的轮胎模型是进行车辆建模和动力学仿真的关键。本文中选择经典魔术公式作为轮胎模型。

轮胎侧向力Fc与轮胎侧偏角α的关系如图2所示。从图中可以看出，在轮胎侧偏角α较小时，轮胎所受侧向力Fc与α呈线性关系。

图2 轮胎侧向力与侧偏角的关系

前、后轮胎所受侧向力Fcf、Fcr公式[8]为

(3)

(4)

式中Ccf、Ccr分别为前、后轮侧偏刚度。

将上述简化后的轮胎模型式(3)、(4)代入式(1)、(2)，并将车辆坐标系xoy转换成惯性坐标系XOY，在前轮转角δf较小时，基于线性轮胎模型，得到车辆动力学非线性模型为

(5)

(6)

(7)

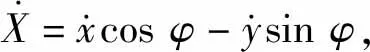
(8)

2 MPC设计

2.1 MPC原理

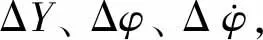
由于MPC原理推导过程已有很多学者进行了详细介绍，因此仅给出必要的文字叙述及关键公式。车辆的非线性动力学模型的状态空间表达式为

(9)

车辆在高速行驶时，对控制器实时性要求更严格，非线性模型预测控制不能满足需求，因此需要对式(9)即车辆非线性模型进行近似线性化。设参考点为(Xr,ur)，在该点对式(9)进行一阶泰勒展开。虽然无法直接将状态变量与控制量变成线性关系，但是可以对状态变量和控制量误差进行线性化。误差的连续状态空间方程为

(10)

线性化后的连续状态空间方程无法进行MPC的递推运算，因此采用一阶差商的方法对模型进行离散化，并作转换

(11)

得到k时刻基于控制增量的状态空间表达式为

(12)

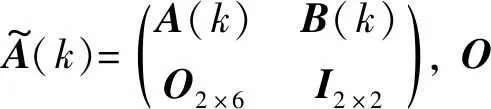
为了说明线性时变模型对车辆未来时刻输出的预测，对所得到的基于控制增量的状态空间表达式进行迭代，可得预测输出表达式。最终都可以转化为带有控制量极限约束和控制增量约束的二次规划问题[9]，即

J[ζ(t),u(t-1),ΔU(t)] ,

s.t. ΔUmin≤ΔUt≤ΔUmax,

Umin≤ΔUt+Ut≤Umax,

yhc,min≤yhc≤yhc,max,

ysc,min-εI3Np×1≤ysc≤ysc,max+εI3Np×1,

ε>0 ,

(13)

式中：J为MPC优化目标函数；u(t-1)为上一时刻控制量；ΔUt、ΔUmax、Umin分别为t时刻的控制增量及其上、下限；Ut、Umax、Umin分别为t时刻的控制量及其上、下限；yhc、yhc,max、yhc,min分别为硬约束输出量及其上、下限；ysc、ysc,max、ysc,min分别为软约束输出量及其上、下限；Np为预测时域；ε为松弛因子，防止控制周期内无法求出最优解。

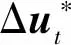
(14)

在每个控制周期循环此过程，即可实现车辆对期望路径的跟踪。

2.2 附加横摆力偶矩控制机理及分配逻辑

(15)

aFcf-bFcr+2cFlr=0，

(16)

式中c为轮胎到车辆纵向中轴线的距离，即轮距的1/2。

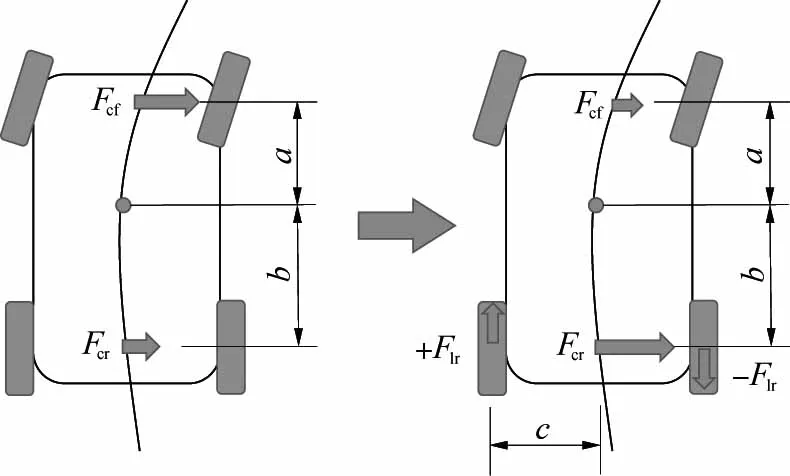
Fcf、Fcr—前、后轮胎的侧向力；a、b—车辆质心到前、后轴的距离；c—轮胎到车辆纵向中轴线的距离，即轮距的1/2；Flr—附加作用力。图3 稳态转向行驶时车辆受力平衡

从式(16)中可以看出，此时Fcf减小，Fcr增大；相应的前侧偏角αf减小，后侧偏角αr增大，车辆的不足转向量减小。如果作用相反的横摆力偶矩M，则车辆的过度转向量减小，因此，作用于车辆的横摆力偶矩M可以改变前、后车轮地面侧向反作用力Fcf、Fcr的大小，并改善车辆的稳态转向特性，显著改善车辆的操纵稳定性。

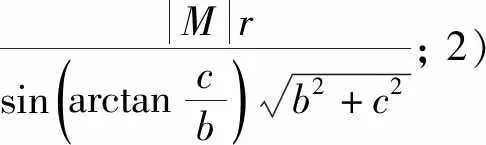
设附加横摆力偶矩M逆时针方向为正，该逻辑采用单轮制动，并且基于下列已知事实：1)左、右车轮制动比前、后车轮制动对车辆转向影响更明显；2)外侧车轮制动可有效改善转向过度，而内侧车轮制动可有效改善转向不足。

3 仿真与分析

基于车辆模型的建立，结合MPC的设计思路，采用CarSim与MATLAB Simulink软件联合仿真，对车辆在冰雪路面(附着系数μ=0.3)和干燥沥青路面(μ=0.85)上以不同车速(54、72 km/h)跟踪双移线轨迹的情况进行分析，联合仿真控制器结构如图4所示。

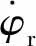
φr—期望横摆角；期望横摆角速度；Yr—期望轨迹；车辆在x、y轴方向的速度；φ—车辆横摆角；车辆横摆角速度；X—行驶距离；Y—实际轨迹； Tfl、Trl、Tfr、Trr—左前轮、左后轮、右前轮、右后轮制动力矩；δf—前轮转角；M—附加横摆力偶矩。图4 车辆模型的联合仿真控制器结构

MPC求解出最优的前轮转角δf和附加横摆力偶矩M，并将附加横摆力偶矩以上述分配逻辑分配给4个车轮制动力矩，并输出给车辆模型，实现闭环最优控制。仿真车辆关键参数和模型预测控制器参数如表1、2所示。

表1 仿真车辆关键参数

3.1 中低速行驶工况仿真

车辆以车速54 km/h行驶，跟踪一段双移线轨迹，通过设置不同的路面附着系数，分析车辆在不同路面上对期望轨迹的跟踪性能和控制稳定性。不同路面上路径跟踪、各轮胎滑移率仿真结果如图5、6所示。

表2 模型预测控制器参数

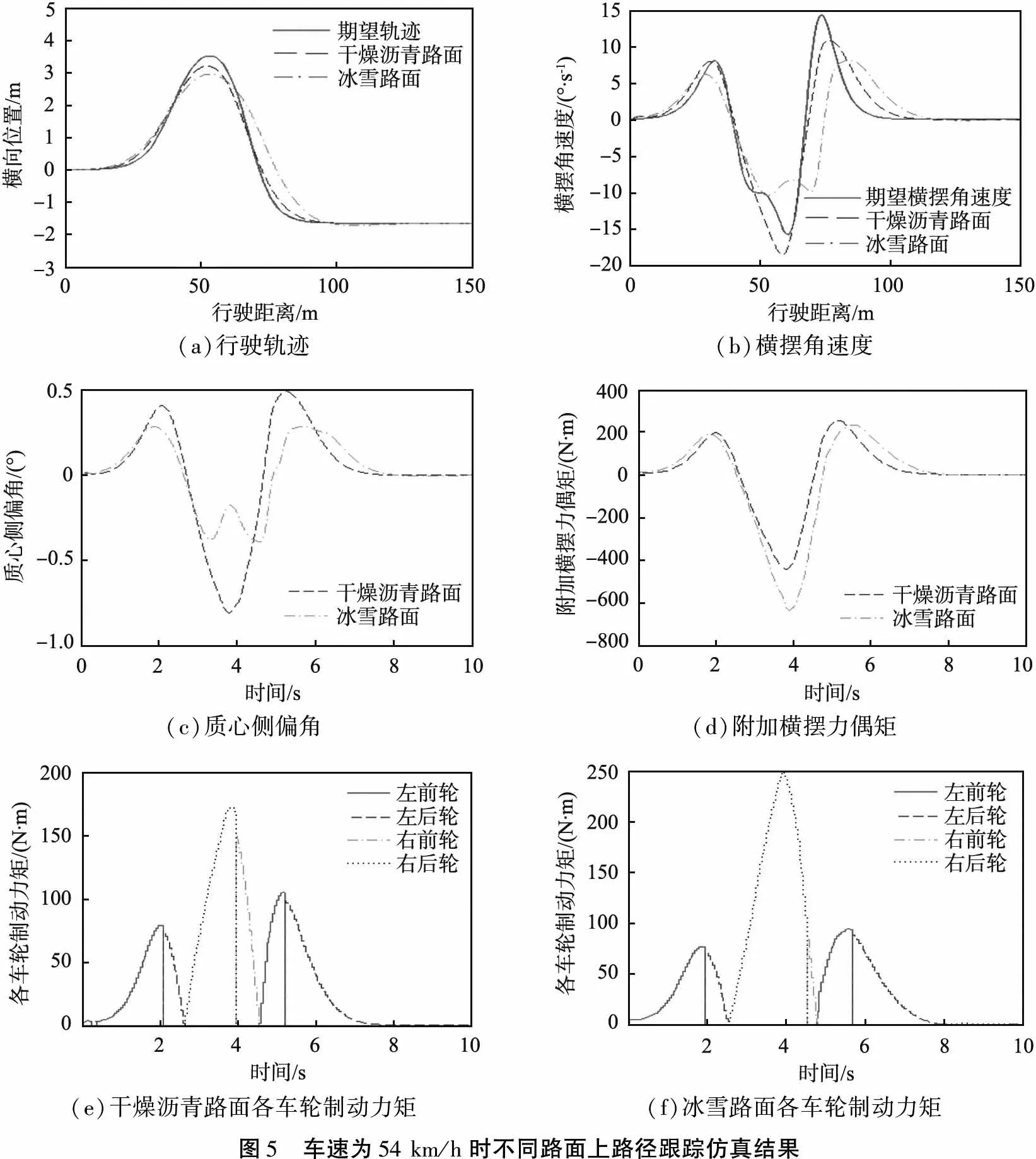
从图5(a)、(b)、(c)中可以看出，当车辆中低速行驶时，在2种路面条件下的跟踪效果仍然良好，冰雪路面上的横摆角速度较小，横摆角速度保持在-10～10 (°)/s，有利于车辆的操纵稳定性，干燥沥青路面上的横摆角速度稍大，约为冰雪路面上的1.55倍，但是车辆仍然稳定；质心侧偏角稳定控制在-1°～0.5°，符合质心侧偏角在冰雪路面上的极限值约束。从图5(d)、(e)、(f)中可以看出，车辆行驶在冰雪路面上时制动力矩较大，原因是滑移率增大，制动力矩效率下降，干燥沥青路面上的制动力矩约为冰雪路面上的80%；结合图5(a)、(d)中的转向和制动曲线可以看出，在0.5 s时车辆开始左转向，在同一时间控制器中，通过制动左侧轮胎给予车辆一个正的附加横摆力偶矩；在2.5 s时车辆右转向，控制器释放左侧的制动，在右侧制动，以产生负的附加横摆力偶矩；从4.5 s开始车辆再次左转向，车辆需要一个正的附加横摆力偶矩，因此制动左侧轮胎。上述结果说明，在控制器的作用下转向和制动实现了良好配合。

从图6中可以看出，车辆在过弯道的极限工况下，2种路面上各车轮的滑移率出现不同程度的震荡，干燥沥青路面上各车轮的滑移率均为-0.3%～0.3%，冰雪路面上最大滑移率出现在右前轮，为1.4%，在合理范围内。

3.2 高速行驶工况仿真

车辆以车速72 km/h行驶，不同路面上路径跟踪、各轮胎滑移率的仿真结果如图7、8所示。

从图7(a)、(b)、(c)中可以看出，当车辆以较大车速行驶时，在干燥沥青路面上仍有较高的跟踪精度，而在冰雪路面上则有一定的跟踪误差，但是质心侧偏角更小，约为干燥沥青路面上的60%，有利于车辆的稳定性控制。从图7(d)中可以看出，车辆在冰雪路面上行驶时需要更大的附加横摆力偶矩来矫正车身姿态。图7(e)、(f)的不同之处不仅在于各轮制动力矩的极值，而且体现在车辆2 s后开始过第2个弯道，干燥沥青路面上过弯道时间仅为1 s，而冰雪路面上则持续了2 s，过弯道时间更长，转弯半径更大，这是控制器为了保证车辆稳定性而对前轮转角和附加横摆力偶矩所进行的优化处理。

从图8(a)中可看出，滑移率被限制在-0.4%～0.6%，制动效率更高。从图8(b)中可以看出，冰雪路面上最大滑移率为1.8%，出现在3 s时的道路曲率最大处。

4 结论

本文中根据具有2个控制输入量的六阶简化自行车模型和附加横摆力偶矩作用原理，设计了MPC路径跟踪控制器，在CarSim和MATLAB Simulink软件联合仿真平台上验证了控制器在不同车速、不同路面附着系数工况下的控制效果。

1)当车辆以中低速行驶时，控制器在2种路面条件下都有很好的跟踪效果以及较强的稳定性，并且具有很强的鲁棒性，横摆角速度均被限制在-20～15 (°)/s，车辆质心侧偏角保持在-1°～0.5°。

2)当车辆以较高车速行驶时，在干燥沥青路面上的跟踪效果仍然较好。在冰雪路面上虽然仍然保持了行驶稳定性，但是牺牲了一定的跟踪精度，原因是车辆模型不够精确。后续将通过采用更大自由度的车辆模型以及更全面的控制算法来解决该问题。