基于LQR/PID控制飞机俯仰角的仿真研究

李卫卫，李 凌

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

飞机在空中飞行时，飞行参数会受到高度、马赫数的影响，而且俯仰姿态也会发生变化.因此，为使飞机能够平稳飞行就需要设计合适的控制器.现阶段国内外有很多对飞机俯仰姿态的研究，现代飞机的设计主要依靠自动控制系统来控制飞机各个子系统.自动控制系统的进步在飞机的发展中发挥了重要作用.通常，飞机的飞行运动包含3个旋转运动和3个平移运动，飞机的控制策略可分为横向控制和纵向控制[1].其中，俯仰控制是一种纵向控制，因此可以采用飞机纵向模型设计飞机的俯仰角控制器.在纵向控制中，俯仰角被控制，飞机的俯仰可以看作绕侧轴旋转，它是水平线上的速度方向与垂直平面之间的夹角，另外，偏转角用于控制位于飞机后部的俯仰.在过去，许多研究人员做过控制飞机的俯仰、滚转和偏航以稳定飞机的研究工作，这一课题至今仍是一个具有挑战性的问题[2-3].针对飞机俯仰姿态以及俯仰角的控制已经有多种方法，例如基于遗传算法的LQR和PID控制器[4]，模糊PID控制[5]，GA调谐LQR和PID控制器[6]，混合EKF和NDO的鲁棒自适应控制器[7]，串级 PID 控制方案所设计的P-PID和PD-PI控制器[8]，H∞控制理论应用于飞机俯仰角控制系统的设计[9]等.

本文主要介绍了飞机俯仰角的基本控制方法LQR控制器和PID控制器.LQR控制响应速度快，跟踪性能好，在LQR的设计中，可手动调节增益k的值，使性能指标J被优化，但是会存在不确定性，这时将预补偿器加入控制回路中，利用MATLAB仿真对LQR控制器进行整定，得到了控制器Q矩阵的最优值，主要目的是减少上升时间、稳定时间和峰值超调.在PID控制器设计中，通过P，PI，PID仿真结果分析对比，可发现PID控制器的控制回路结构简单，当系统中出现扰动时，PID控制器可使系统平稳，并且通过参数整定可使上升时间和调节时间加快，稳态误差和超调量都减小.以飞机的俯仰角为输出，在MATLAB环境下对这两种控制方案进行仿真分析并与原系统进行比较，讨论2种控制策略对飞机系统性能的影响，给出了飞机俯仰角响应的MATLAB仿真结果，并以飞机俯仰角响应的上升时间、峰值超调和稳态误差为指标进行性能测试.

1 系统建模

飞机运动方程是一组非常复杂的6个非线性耦合微分方程组,而且飞机俯仰角的模型是时变、非线性的.假设飞机的速度和高度是恒定的，而且俯仰角的改变不会影响飞机的速度，它们可以解耦并线性化为纵向和横向方程.飞机俯仰受纵向动力学控制，这里将设计一个自动驾驶仪来控制飞机的俯仰.

如图1所示，假设重力、阻力、升力和推力在x,y方向上，并且在高空飞行时俯仰角的改变不会影响飞机的速度.文中主要研究飞机的俯仰角θ以及偏转角δ，通过推导[10]可得出飞机的纵向运动方程：

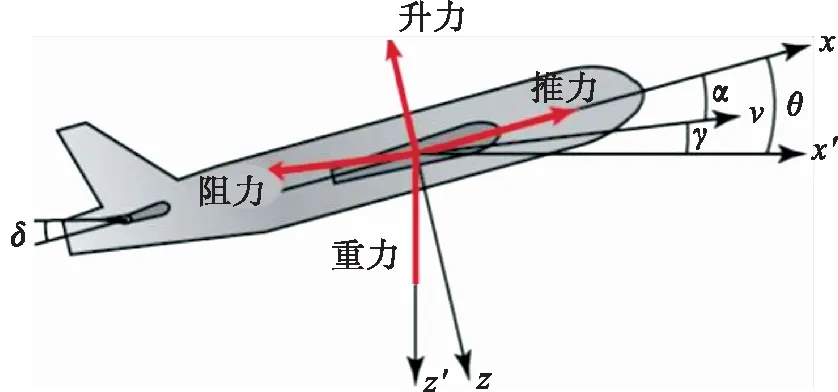
图1 飞机受力分析Fig.1 Aircraft force analysis

(1)

[CM+σCM(1-μCL)]q+

(ηCWsinγ)δ],

(2)

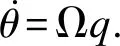
(3)

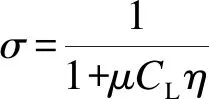
(4)

(5)

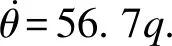
(6)

在零初始条件下，经过拉普拉斯变换可以得到传递函数：

(7)

将其整理成状态空间模型：

(8)

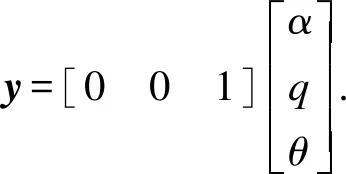
(9)

根据状态空间模型(8)、(9)，通过SIMULINK搭建出控制对象，在开环状态下，当输入为一个阶跃响应时，其输出如图2所示，由图2可见，俯仰角是没有趋于稳定值的，即系统是不稳定的.而为了使飞机能够平稳的飞行，将设计反馈控制形成闭环，使飞行中实际俯仰角的控制能够满足表1中各个参数的基本要求.

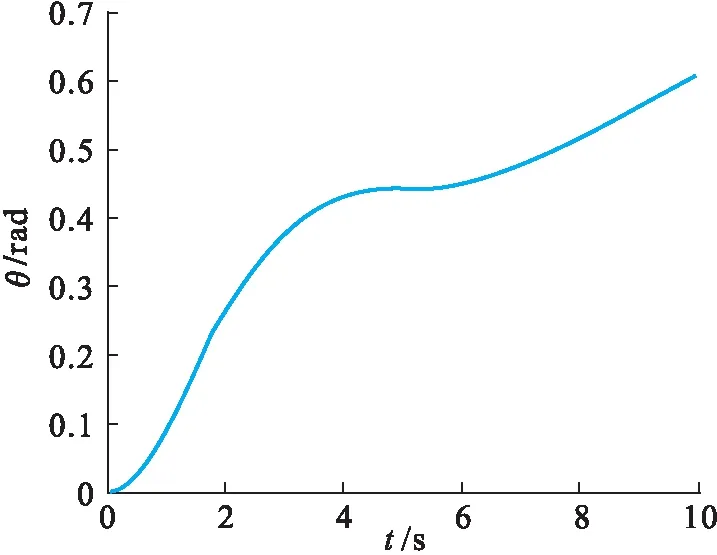
图2 开环阶跃响应Fig.2 Open-loop step response

表1 性能指标要求Table 1 Performance requirement

2 控制器设计

2.1 LQR控制器

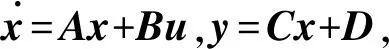
(10)

线性定常系统可通过状态反馈控制实现n个极点任意配置的充要条件是被控系统∑0(A，B，C)态完全能控.通过验证rank[B,AB,A2B…An-1B]即rankQc，或用MATLAB环境编写命令，若满秩则为完全能控.系统的能控矩阵是3×3，经计算秩为3，则系统可控，可以设置一个全状态反馈控制系统(见图3)实现极点的任意配置.

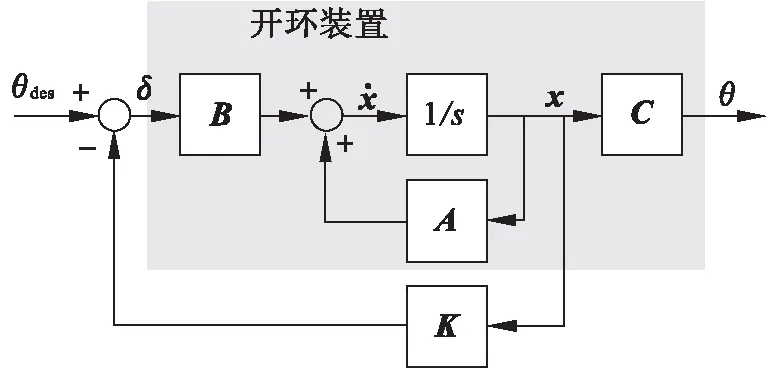
图3 全状态反馈系统原理Fig.3 Full state feedback system schematic diagram

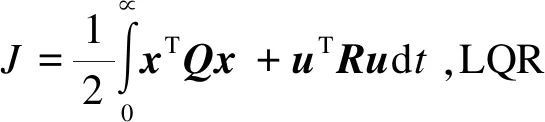
2.2 PID控制器

图4为控制系统的基本结构，其中PID控制器[13]的传递函数为

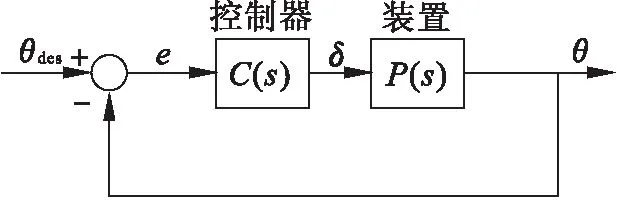
图4 系统结构模型Fig.4 System structure model

(11)

通过MATLAB仿真观察输出响应，判断PID是否满足飞机俯仰角的4个性能要求.

首先，加入P控制器C(s)=Kp，可以提高系统的开环增益，减小系统的稳态误差从而提高系统的控制精度.设定参考阶跃响应为0.2 rad，设置比例系数Kp=1，判断此时所产生的波形是否稳定.若不稳定，需要多次反复检验.若是控制器满足了上升时间稳态误差以及超调量的要求，但是调节时间过大，此时需要在控制器中加入微分或积分项以加快响应满足要求.

3 系统仿真研究

假设飞机是在恒定的速度以及高度下驾驶，而且飞机俯仰角θ的改变不会影响飞机的速度，通过SIMULINK设计一个自动驾驶仪，采用LQR控制以及PID控制对比分析效果.为使飞机能够平稳驾驶，对θ进行研究，使其满足超调小于10 %，上升时间小于2 s,调节时间小于10 s，稳态误差小于2 %.

3.1 LQR控制器

建立SIMULINK[14]闭环状态下的模型观察响应是否满足要求.在模型的建立中，阶跃响应终值设置为0.2，状态空间模块使用飞机状态空间模型的参数.作为单入单出系统，示波器显示的是飞机俯仰角θ的变化.

图5所示为闭环控制系统结构，在开环系统的基础上增加一个反馈控制增益，这个增益由线性二次调节器LQR[15]设计，可以先使用Riccati方程求解，或用MATLAB环境lqr命令，具体值K=[-0.643 5，169.695 0，7.071 1]，此时示波器所产生的波形如图6所示.由图6可以看出飞机俯仰角θ是稳定的，调节时间、上升时间、超调量都满足要求，但存在稳态误差，需要在闭环系统的基础上添加预补偿器，如图7所示.

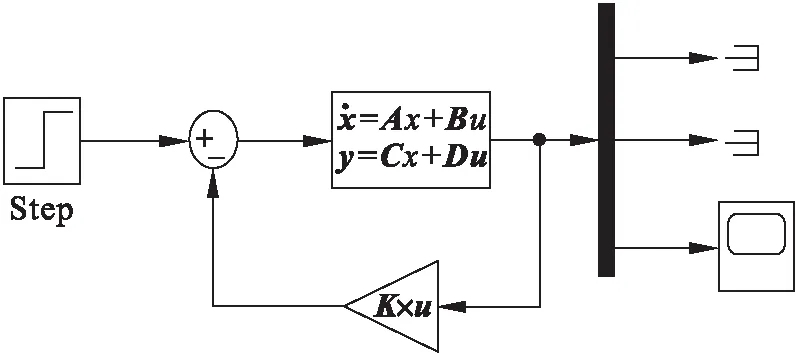
图5 闭环控制系统Fig.5 Closed-loop control system

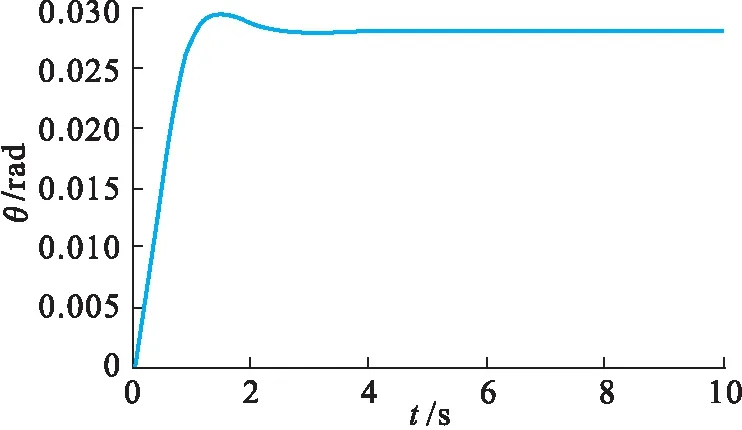
图6 闭环阶跃响应Fig.6 Closed-loop step response

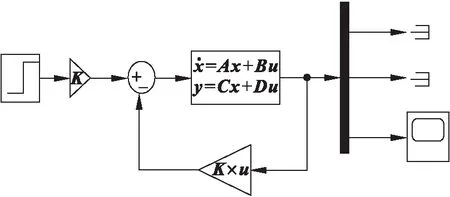
图7 添加预补偿器Fig.7 Added pre-compensator

在线性二次调节之后，稳态误差过大，需要缩放基准输入，使输出在稳态下等于基准.其中缩放因子可以通过MATLAB用户自定义函数自动生成，在这里缩放因子N=7.071 1.此时，波形如图8所示，俯仰角θ超调量为5 %，上升时间为1.15 s，调节时间为2 s，稳态误差为0.2 %，满足各项要求.

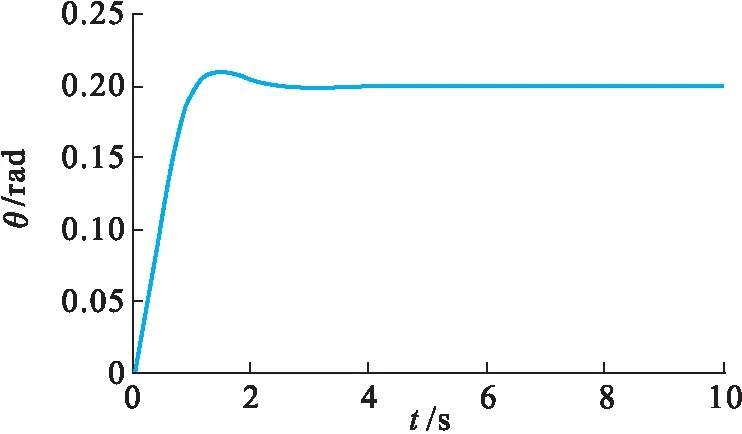
图8 预补偿后输出θ波形Fig.8 Waveform output after adding pre-compensator

3.2 PID控制器

因为预补偿器是根据被控对象的模型计算的，而且位于反馈回路之外，所以预补偿器存在弊端.当系统存在误差或未知扰动时，预补偿器不能将其校正，会存在稳态误差.为了消除误差，需要添加PID控制器[16]进行自动整定.

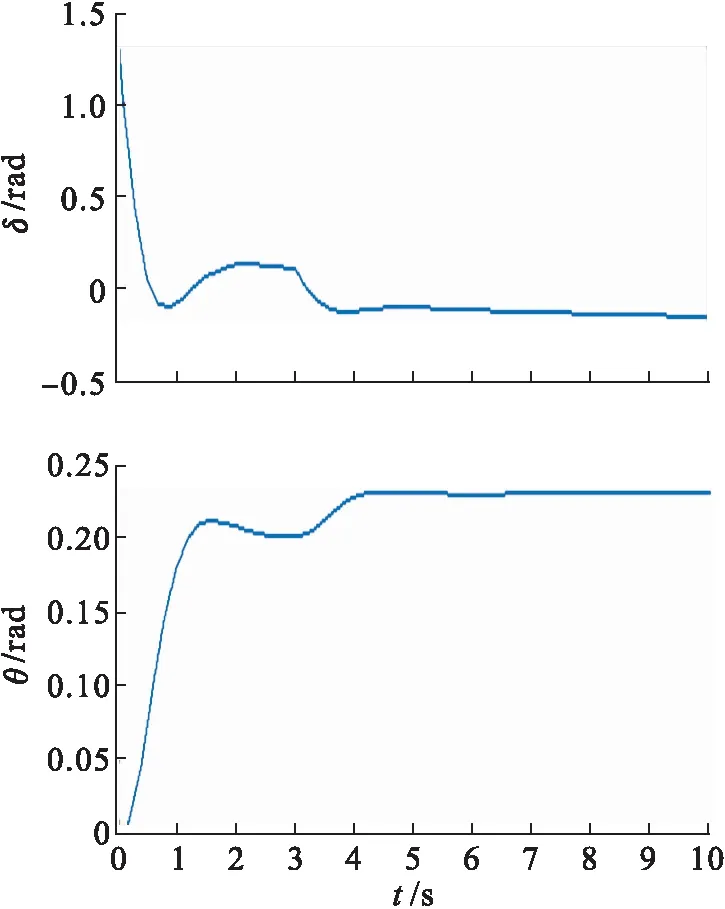
图9 添加扰动后波形Fig.9 Added disturbance waveform

将LQR控制器与PID控制器的控制效果进行对比分析，如表2(表2的参数值是由图6、图8和图10的波形分析计算得出)所示，与闭环控制系统相比，在PID控制器以及LQR控制器下的飞机俯仰角的控制系统的确能够较好地消除飞机在飞行中受到干扰时的俯仰角偏差，缩短飞机在飞行中趋向稳定的时间，加速响应，减少了上升时间，并且LQR与PID相比较效果更好.

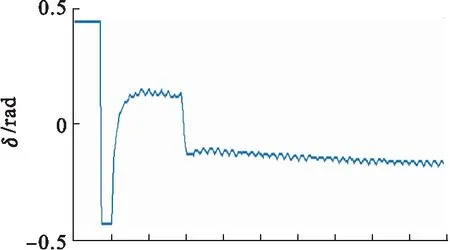
图10 PID系统产生波形Fig.10 Waveform generated by PID system

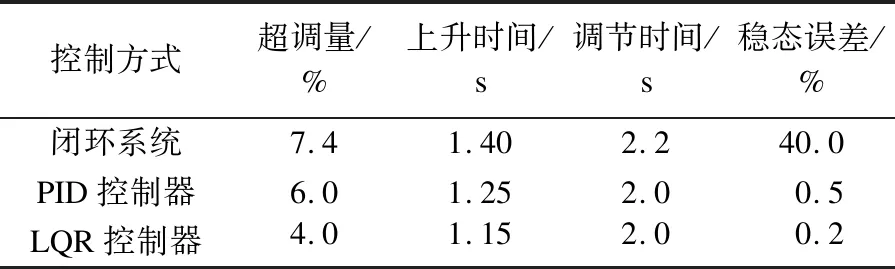
表2 性能指标对比Table 2 Comparison of performance indexes

4 结 论

由于周围环境等诸多因素，飞机会受到干扰和噪声的影响，从而导致系统的振动、稳态误差和响应时间的延长.本文通过设计LQR控制器和PID控制器来实现对原系统的控制，LQR控制器提供了最小的可能振动和更好的响应速度，它需要加入预补偿器缩放输入基准；为了测试PID控制器的性能，要通过添加扰动来实现.

在2种控制方法中，PID控制器的控制效果稍差一些，由于PID控制器的比例、积分、微分参数靠经验或者多次实验获得，当系统性能发生变化或者遇到干扰后，整定的参数不一定适用，但PID控制器因具有结构简单、设计原理易于掌握和鲁棒性强等优点，广泛应用于工业控制中.LQR控制器是通过对系统进行局部线性化的方法进行控制的，其抗干扰性和鲁棒性效果较好，LQR控制器比PID控制器能更好地实现对俯仰角的控制，具有响应快，超调小，稳态误差小的优势，能够更好地满足要求，使飞机处于平稳状态，飞行更加舒适安全.