含减震外挂墙板的装配式框架结构协同抗震性能研究

种 迅，侯林兵，解琳琳，王心宇，陈 曦

(1.合肥工业大学土木与水利工程学院，合肥 230009；2.北京建筑大学土木与交通工程学院，北京 100044；3.北京市建筑设计研究院有限公司，北京 100045)

预制混凝土夹心保温外墙板被广泛应用于各类装配式建筑结构中[1−3]，这主要是由于其工业化程度高且具有良好的保温和耐久性能。当该类墙板用于钢筋混凝土结构时，我国常采用刚性线连接方式，即墙板顶部通过钢筋与叠合钢筋混凝土梁进行连接，底部通过限位连接件(允许一定滑动变形)与下层梁进行连接[4−6]。

鉴于墙板与主体结构间会产生一定程度的相对水平变形，笔者提出了新型减震外挂墙板(energy dissipation cladding panel，EDCP)，即采用U型金属阻尼器取代底部的限位连接件形成一种柔性耗能减震连接，该墙板可有效利用主体结构和围护墙板之间的相对水平变形耗散地震能量，使得两者协同工作共同抗震。研究团队开展了含EDCP的足尺装配式壁式框架子结构抗震性能试验研究，验证了该协同抗震体系的合理性[7]。在减震外挂墙板领域，国外部分学者也开展了相关研究工作，Baird等[8]在一个单层单跨的弹性柱底铰接框架和外挂墙板间顶部采用U型阻尼器，底部采用承重连接，并对这一结构进行了拟静力试验研究，结果表明带有U型阻尼器的结构与原来的弹性柱底铰接框架结构相比，耗能能力、承载力和刚度有了明显提高；Karadoğana等[9]在外挂钢筋混凝土板的底部和外挂板间同时布置U型阻尼器，顶部采用了单点连接引导板体摇摆变形，这种连接方式可增大两处U型阻尼器的相对变形，但也会引起底部阻尼器的竖向拉压。值得注意的是，上述研究中，前者的主体结构为较特殊的弹性框架，仅依靠阻尼器耗能，且墙板与主体结构间连接方式也与本文有明显区别。后者则仅是针对于外挂墙板耗能连接本身展开研究，并未对外挂墙板与主体的协同抗震展开研究。更重要的是，上述研究均未对该类结构的减震特征开展深入研究。

为了探究上述含EDCP结构的抗震性能和协同减震机理，本研究首先基于前期开展的含EDCP的装配式壁式框架结构试验[7]，提出并验证了适用于该类结构的多尺度数值模拟方法。在此基础上，设计了一栋8层RC框架结构，基于多尺度数值模型对比了传统框架结构和含EDCP的框架结构的地震响应异同，初步明确了该类结构的协同减震效果和地震损伤特征。为了充分明确关键设计参数(刚度比和屈服力比)对结构减震机理的影响规律，本研究设计了28个具有不同设计参数的减震案例，重点分析了关键设计参数对减震效果、各类构件塑性耗能特征和主体结构损伤控制的影响规律。本文的研究成果可为主体和围护协同一体化工作的高性能结构体系研发和抗震性能研究提供重要参考。

1 含EDCP的装配式壁式框架数值模拟方法

1.1 试验简介

研究团队前期设计制作了一足尺单层单跨含EDCP的装配式壁式框架结构试件，进行了低周反复荷载下的抗震性能试验研究。同时对结构试件中所采用的U型金属阻尼器开展了抗震性能试验研究。上述系列试验信息详见文献[7]，下面简要介绍用于数值模拟方法研究的关键信息。

U型阻尼器(图1(a))的平直段有效长度L为95 mm，钢板宽度B为70 mm，钢板厚度t为12 mm，圆弧段中心线半径R为66 mm，钢材等级为Q235，实测屈服强度、极限强度和伸长率均值分别为268 MPa、331 MPa和28.4%。试验全过程中仅圆弧段与平直段交界处附近的钢板表面出现较轻微的裂纹，整体未见其他破坏现象，呈现出较理想的履带式变形，试验所得滞回曲线如图1(b)所示，结合试验现象可以看出所采用的U型阻尼器具有良好的耗能能力。

图1 U型金属阻尼器尺寸及试验滞回曲线Fig.1 Dimensionsof U-shaped steel damper and tested hysteretic curve

含EDCP的装配式壁式框架结构试件截面尺寸和配筋如图2所示。为保证外挂板能与梁共同变形，设计外挂墙板与梁之间的连接时，沿着梁长设置了连接钢筋和抗剪键槽。为了避免外挂板对梁端受弯产生影响，在进行连接时避开了梁两端塑性铰区。外挂墙板下方设置4个U型阻尼器，阻尼器两两一组对称布置于墙板下方2个预留的孔槽内，与基础底座及外挂墙板间均采用螺栓连接。混凝土强度等级均为C30，实测预制剪力墙、梁混凝土立方体抗压强度和预制夹心保温外挂墙板混凝土立方体抗压强度分别为42.91 MPa和28.51 MPa。钢筋强度等级均为HRB400，钢筋材性如表1所示。

表1 钢筋材性Table 1 Mechanical properties of reinforcement

图2 结构试件截面尺寸和配筋Fig.2 Dimensionsand reinforcement detailsof specimen

试件设计轴压比为0.2，对应的轴力为343 kN。水平荷载采用荷载-位移混合控制加载。试件关键损伤特征包括：1)试件顶点加载至2.81 mm时，阻尼器首先进入屈服，此时梁和墙肢纵筋均未屈服，结构整体处于弹性状态。整个加载过程中，连接阻尼器和结构的螺栓未出现松动和滑移，阻尼器仍可维持履带式变形，且变形与顶部位移基本一致，能够稳定耗能；2)在试件顶点位移达到8 mm和9 mm时，墙肢根部和梁端分别形成塑性铰。顶点位移达到60 mm时，墙肢根部混凝土压碎。试件破坏整体呈现出较为明显的梁铰机制破坏特征；3)外挂墙板仅在加载后期在洞口角部和下方出现轻微裂缝，整体损伤程度较轻。试件最终破坏情况如图3所示。

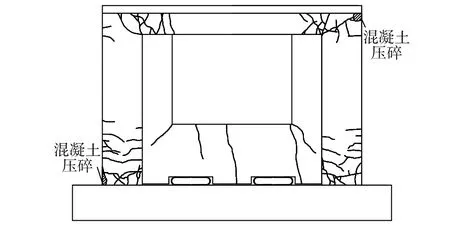
图3 试件破坏示意图Fig.3 Failure mode of specimen

1.2 数值模拟方法

结合试验破坏特征，本文提出了适用于该类结构的多尺度数值模拟方法(如图4所示)，并基于Perform-3D建立模型。具体而言：

1)墙肢和梁采用纤维模型模拟[10]，这主要是由于两者整体呈现出明显的弯曲破坏特征，传统纤维模型可以较好地反映该类特征，墙肢离散为9个纤维单元，梁离散为8个纤维单元，墙肢和梁的截面纤维网格划分方案如图4所示。钢筋采用双折线模型，材料性质与试验数据保持一致，混凝土采用修正的Kent-Park模型计算约束和非约束混凝土本构参数。

2)外挂墙板采用刚性柱模拟，这主要是试验中外挂板未出现明显损伤且刚度较大，能够有效协调主体结构和U型阻尼器的变形。

3)U型阻尼器采用弹簧单元模拟，本构采用双折线模型，可较好地模拟其水平滞回受力特征。由于阻尼器的竖向变形和竖向刚度均较小，忽略阻尼器竖向力对结构的影响。

首先基于既有公式标定弹簧模型关键参数，需要明确阻尼器的初始刚度K0、屈服承载力Fy及屈服后刚度KF。本研究在此采用Baird等[11]提出的初始刚度和阻尼器全截面进入屈服时强度的理论式(1)和式(2)计算。

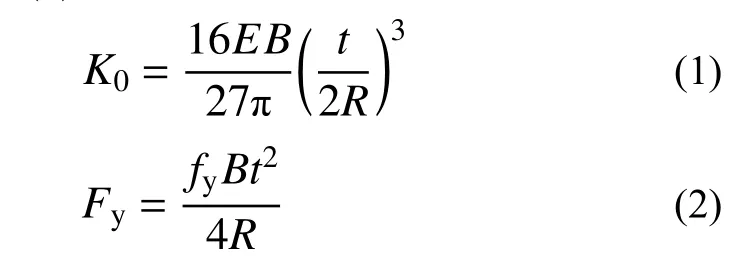
式中，E为钢材的弹性模量。阻尼器屈服后刚度KF取为0.03K0[12]。采用上述方法模拟的滞回曲线与试验曲线对比如图5所示。从图5可以看出，两者骨架曲线吻合良好，滞回耗能特征略有差异，但总累积耗能能量误差约为4%，整体还在工程应用可接受范围内。

图5 阻尼器模拟与试验结果对比Fig.5 Comparison between simulated and experimental resultsof tested damper

基于上述模拟方法，本研究对试验试件在低周反复荷载作用下的受力行为进行了模拟，其滞回曲线与试验曲线对比如图6所示。总体上两者滞回曲线吻合较好，阻尼器首先屈服，塑性铰首先出现在墙肢根部，随后出现在梁两端，最终因墙肢混凝土进入退化引起构件承载力降低，整体损伤演化模式与试验基本一致，验证了本文建议的方法具有一定的合理性和可靠性。

图6 试件模拟和试验滞回曲线对比Fig.6 Comparison between simulated and experimental hysteretic curvesof tested specimen

2 含EDCP的装配式框架减震特征

2.1 抗震结构的地震损伤特征

本研究设计了一栋8层钢筋混凝土框架结构，长28.8 m、宽15.9 m、高29.7 m，底层、第2层和其余楼层层高分别为4.2 m、3.9 m和3.6 m。设防烈度为8度(0.20g)，场地类别为Ⅱ类场地，设计地震分组为第一组，场地特征周期为0.35 s。相应的平面图和立面图如图7所示。第1层、第2层～8层柱截面尺寸分别为650 mm×650 mm，600 mm×600 mm，梁截面尺寸均为300 mm×650 mm。混凝土强度等级均为C35，钢筋强度等级为HRB400，楼板厚度均为110 mm。

图7 结构示意图/mFig.7 Schematic diagram of structure

基于Perform-3D，采用上文建议方法建立整体结构模型，计算结构前3阶周期分别为1.176 s(X向平动)、1.102 s(Y向平动)和1.01 s(扭转)。为充分揭示抗震结构和减震结构的地震响应特征，本文根据《建筑抗震韧性评价标准》[13]建议，选取了11条地震动(包括8条天然波和3条人工波)对结构进行抗震性能分析，天然波信息如表2所示，相应地震动的加速度反应谱与规范设计反应谱的对比如图8所示。需要说明：本研究在选取地震动时综合考虑该抗震结构和后续减震结构分析需求，控制其在1.176 s(抗震结构周期)和0.678 s～0.950 s(系列减震结构周期段)内各地震动反应谱值与规范反应谱在统计意义上相符，单条谱值误差不超过35%，均值误差不超过20%。

表2 地震波信息Table 2 Information of ground motions

将上述地震动沿X轴方向输入进行罕遇地震下的动力时程分析。计算所得的11条地震动下结构最大层间位移角及其平均值如图9(a)所示，11条地震动下最大层间位移角均值为1/106，满足规范[14]要求。为了进一步明确含减震外挂墙板框架结构的地震耗能模式和构件损伤的控制能力，本研究在此统计了11条地震动下结构的各类构件塑性耗能沿高度方向的均值分布以及达到不同损伤等级的构件数目，相应结果分别如图9(b)和图9(c)所示。梁柱构件的损伤等级确定采用《建筑抗震韧性评价标准》[13]中建议的方法确定，对于梁柱均基于钢筋和混凝土应变判定其损伤程度，包括完好、轻微、轻度、中度和重度。从图9(b)中可以看出，地震下梁构件损伤主要集中于1层～4层，柱构件的损伤主要集中于第1层。从图9(c)可以看出，绝大部分柱均处于完好状态，底层的8根柱达到了轻微损伤状态，仅2根柱进入了中度损伤状态，这是由于在某一条地震动下底层柱损伤程度较大。对于X向的框架梁，有23根、54根和5根梁分别进入了轻度、中度和重度损伤状态，29根和17根梁处于完好和轻微损伤状态。相对于柱构件，梁构件损伤较为严重，反映了结构满足“强柱弱梁”的设计要求。

图9 抗震结构分析结果Fig.9 Analysisresultsof seismic structure

2.2 含EDCP的减震结构的地震响应特征

在上述抗震框架结构的基础上，附加减震外挂墙板，对应布置方案如图10所示。具体而言，每跨布置一块减震墙板，安装4个相同的U型阻尼器，每层共32个阻尼器，阻尼器设计参数如表3所示，表中参数含义见1.1节。阻尼器采用Q235钢材，弹性模量为2×105MPa，屈服强度设计值fy为215 MPa，根据1.2节校验过的公式预测阻尼器屈服荷载为21.03 kN，初始刚度为8.371 kN/mm。

图10 减震外挂墙板布置方案Fig.10 Setup of energy dissipating cladding panels

表3阻尼器设计参数Table 3 Design parametersof damper

基于Perform-3D，采用1.2节校验的模拟方法建立减震结构的弹塑性模型，结构前3阶周期分别为0.950 s(X向平动)、0.910 s(Y向平动)和0.635 s(扭转)。对结构X轴方向输入2.1节中的11条地震动进行罕遇地震下的动力时程分析。计算所得的11条地震动下结构最大层间位移角及其平均值如图11(a)所示。11条地震动下最大层间位移角均值为1/137，与抗震结构相比减小了22.3%。为评估增设阻尼器对结构地震力的影响，本研究统计了抗震结构与减震结构中的主体结构11条地震动下最大楼层剪力的均值，如图11(b)所示。从图中可以看出，在阻尼器对结构刚度和阻尼两个参数的复合影响下，减震结构中主体结构与抗震结构的楼层剪力相差不大，在较高楼层减震结构楼层剪力较小。

表4统计了地震总输入能量、阻尼耗能以及梁、柱和阻尼器塑性耗能的均值，从表4可以看出两者地震总输入能量基本相当，减震结构响应小导致阻尼耗能明显减少。减震结构总塑性耗能显著大于抗震结构，其中84.8%的塑性耗能由减震墙板所含的阻尼器耗散。本研究在此对比了各类构件塑性耗能均值沿结构高度方向分布如图11(c)所示，从图中可以看出除顶层外所有阻尼器均屈服耗能，峰值出现在第2层，向上和向下呈递减趋势。相比于抗震结构，结构第5层～8层梁基本无损伤，第1层～4层梁的塑性耗能得到了显著降低，底层柱仍存在一定程度损伤。

表4 结构能量信息/(kN·m)Table4 Information of structural energy

为进一步明确减震控制效果，本研究统计了各类构件的损伤程度，如图11(d)所示，减震结构中保持完好的构件数目显著增多，重度损伤构件为0，柱均处于完好和轻微损伤状态，中度损伤的X向框架梁由54根降为39根。

图11 减震结构分析结果Fig.11 Analysisresultsof energy dissipation structure

3 协同减震关键设计参数影响规律

3.1 分析案例

阻尼器的设计参数是影响结构减震机制的关键因素，本节主要探讨阻尼器设计参数对围护-主体协同减震结构减震机理的影响规律。由于该结构呈现出较为明显的双重屈服机制，本文借鉴已有研究[15−18]，以整体结构中减震外挂板刚度和屈服力与主体结构刚度和屈服力比值(下文简称为刚度比和屈服力比)为关键设计参数，设计不同案例研究其减震规律。在此过程中，保持主体结构方案不变，且假定结构各层阻尼器方案保持一致。

1)刚度比SR：本文采用整体结构周期来表征刚度比，如式(3)所示，式中TF和TDF分别是空框架结构和含减震外挂墙板的框架结构的一阶周期。

2)屈服力比YFR：通过刚度比和屈服位移比的乘积计算得到，屈服位移比为阻尼器屈服位移与楼层屈服位移(偏于保守按1/550的层高考虑)比值。由于算例结构各层层高不同，本文根据首层的屈服位移计算。

本研究在此考虑了4种刚度比，对于每种刚度比均设计了7种屈服力比，共28个分析案例(如表5)。28个案例均可保证减震墙板的屈服位移不超过主体结构的屈服位移，可保证减震结构先进入屈服耗能。

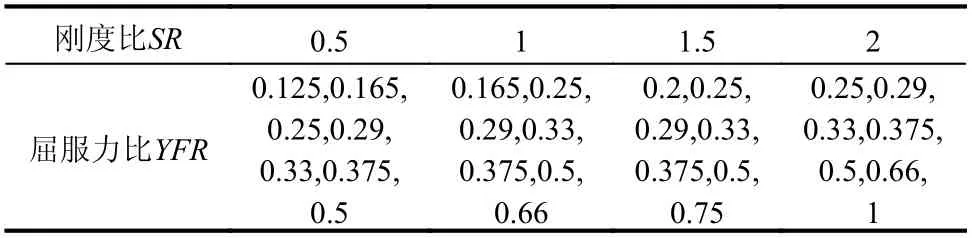
表5 分析案例参数Table 5 Parameters of study cases

3.2 减震率影响性分析

采用第1节建议的模拟方法建立上述28个案例的弹塑性模型，其结构周期介于0.678 s～0.950 s，因此可采用2.1节的11条地震动进行罕遇地震下的动力时程分析。限于篇幅，本文不再列出各案例的层间位移角结果，直接给出各案例的减震效果(damping effect，DE)如图12所示。式(4)中，DrF和DrDF分别为空框架结构和含减震外挂墙板的框架结构的最大层间位移角均值。

从图12可以看出，28个案例的减震率介于18.4%～56.3%，整体随着刚度比和屈服力比的增大而增大。在给定的刚度比下，在屈服力比较小时，随着屈服力比的增大减震率显著提升，当达到一定值后则趋于平稳，如刚度比为0.5时，屈服力比达到0.25后减震效果趋于稳定。随着刚度比的增大，屈服力比的影响规律基本一致，但减震率趋于平稳所需的屈服力比逐渐增大。从图12也可以看出，在相同的屈服力下，减震率的增量随着刚度比的增大有逐渐减小的趋势，刚度比为1.5和2的差别已相对不明显。

图12 刚度比和屈服力比对减震效果的影响Fig.12 Influence of stiffnessratio and yield force ratio on reduction effect

3.3 地震损伤控制影响性分析

为深入研究不同参数对主体结构损伤控制效果的影响，本研究统计了11条地震动下各案例中各类构件塑性耗能沿高度方向的均值分布。限于篇幅，现仅列出刚度比为0.5时，屈服力比分别为0.125、0.25(减震率趋于平稳点)和0.5案例的统计结果，以及刚度比为1时，屈服力比分别为0.165、0.33(减震率趋于平稳点)和0.66案例的统计结果，如图13(a)和图13(b)所示。

从图13可以看出，阻尼器耗能占总塑性耗能的比例较高，且随着屈服力比的增加，这个比例逐渐增大；在给定的刚度比下，随着屈服力比的增加，梁柱塑性耗能逐渐降低，最后趋于平稳。设计参数的变化不会显著改变主体结构的损伤耗能分布特征，梁构件损伤集中于第1层～4层，柱构件损伤只出现在底层，阻尼器耗能峰值出现在第2层，向上和向下呈递减趋势。但阻尼器的耗能分布模式会有所差别，由于阻尼器屈服力的增大，即使薄弱层的位移减小但耗能仍会有所增大，其余楼层则显著减少。

图13 各类构件塑性耗能分布Fig.13 Distribution of dissipated plastic energy of various components

此外，28组案例中的柱均未出现中度和重度损伤，保持完好的梁柱构件数随着刚度比和强度比的增大而增大，中度损伤的梁构件显著减少，柱基本处于轻微损伤状态，个别进入轻度损伤状态。

4 结论

为研究含减震外挂墙板的装配式框架结构的抗震性能，揭示其协同减震机理和关键设计参数对减震机理的影响规律，本文基于前期试验提出了适用于该类结构的多尺度数值模拟方法，通过一栋RC框架结构明确了该类结构的协同减震机理，基于28个案例揭示了刚度比和屈服力比对其减震机理的影响规律。主要结论如下：

(1)提出的多尺度数值模拟方法可较好模拟该类结构的损伤演化模式和主要受力特征，具有一定的合理性和可靠性。

(2)减震墙板中所配置的U型阻尼器可先于主体结构屈服耗能，有效控制结构响应，显著降低损伤梁柱构件的数目和程度，但不改变主体结构损伤演化模式，验证了减震围护墙板与主体结构共同工作且消能减震的可行性和有效性。

(3)随着减震墙板与主体结构刚度比和屈服力比的增大，结构层间位移角减震率和阻尼器耗能与总塑性耗能比增大，当刚度比和屈服力比达到一定值后，该减震率和阻尼器耗能趋于稳定。