H型钢梁与矩形钢管混凝土柱平齐式端板单边螺栓连接节点弯矩-转角分析模型

赵均海，樊军超，高伟琪

(长安大学建筑工程学院，西安 710061)

钢管混凝土节点设计是钢管混凝土组合框架设计的重要组成部分[1−2]。由于外围钢管对混凝土的约束作用，使得钢管混凝土柱具有承载力高、延性好、外形美观和便于施工等优点[3−5]。螺栓端板连接在实际工程中得到广泛应用，特别是在装配式钢结构或避免现场焊接的情况下[6−7]。因此，本文研究的钢管混凝土平齐式端板单边螺栓连接节点(CFSTCEPBB)充分利用了钢管混凝土(CFST)柱和螺栓连接的优点。CFSTCEPBB通过平齐式端板和单边螺栓连接钢梁和普通钢管混凝土柱或复式钢管混凝土柱，构造详情如图1所示。试验结果表明，CFSTCEPBB具有很好的抗震性能和延性[8−10]。

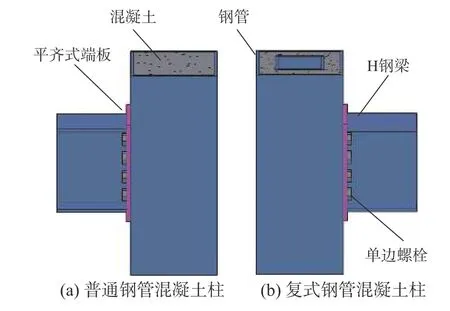
图1 CFSTCEPBB构造Fig.1 Configuration of CFSTCEPBB

节点弯矩-转角关系曲线能够直接反映节点的性能，从该曲线可以得到节点的极限弯矩和初始转动刚度。此外，可以根据节点弯矩-转角曲线的初始斜率确定节点类型，理想刚性节点的初始斜率无穷大，理想铰接节点的初始斜率为零；试验结果表明CFSTCEPBB弯矩-转角曲线的初始斜率介于无穷大和零之间[8−10]，因此CFSTCEPBB可看作半刚性节点。目前，获取节点精确的弯矩-转角关系曲线常用的方法是通过试验研究或有限元分析[11−14]，但是这两种方法的缺点是会产生大量的时间、资金和人工成本，假如节点构造中某一参数改变，则需要进行更多的试验研究和有限元分析，不利于实际工程应用。考虑到实际工程中每个节点构造并不完全一样，理论模型可高效解决节点参数变化的问题。Yee和Melchers[15]提出了钢结构中端板螺栓连接节点弯矩-转角关系四参数模型，并给出了每个参数详细的确定方法。Ataei等[16]通过有限元分析建立组合框架结构中单边螺栓平齐端板连接节点的弯矩-转角关系模型，与试验结果吻合良好。陈学森等[17]基于组件法提出大容量端板节点弯矩-转角关系非线性模型，与试验结果吻合较好，但该模型为分段模型且模型复杂。Zhou等[18]根据节点可能破坏模式建立基于极限弯矩和初始转动刚度的双参数指数模型，基于模型的预测结果和试验曲线吻合较好，但未考虑节点构造形式对节点性能的影响。以上文献中的弯矩-转角关系模型仅适用于特定的节点类型，因此，非常有必要建立适用于CFSTCEPBB的弯矩-转角关系模型。

节点的极限弯矩值和初始转动刚度值是建立弯矩-转角关系曲线模型时所需的2个重要参数[6,19]。对于节点的极限弯矩，考虑所有可能破坏模式下节点的抵抗弯矩，取其最小值作为节点的极限抵抗弯矩[15,18]。确定节点初始转动刚度的方法主要有2种：一种是基于欧洲规范EC3[20]，在节点弯矩-转角曲线中，取M=2/3Mj,RD时的割线刚度作为节点的初始转动刚度，其中Mj,RD为节点的极限抗弯承载力；另一种是基于组件法建立节点初始转动刚度计算模型[21−23]。以上文献中关于极限弯矩的计算方法和初始转动刚度的分析模型均不适用于本文研究的两种CFSTCEPBB，因此对于图1节点类型有必要提出简便、准确的极限弯矩计算方法，建立初始转动刚度分析模型，为建立弯矩-转角关系模型奠定基础。

本文提出了一种新的三参数指数模型，通过确定节点极限弯矩和初始转动刚度、选取节点形状参数预测CFSTCEPBB弯矩-转角关系曲线。考虑CFSTCEPBB的可能破坏模式，建立节点极限弯矩计算模型，基于组件法建立CFSTCEPBB的初始转动刚度计算模型。此外，与试验结果对比验证本文模型的正确性，并给出结论。

1 节点弯矩-转角模型

在半刚性框架结构设计中应充分考虑节点弯矩和转角的关系，然而目前尚未有关于图1所示2种常见CFSTCEPBB的弯矩-转角关系模型，因此有必要建立能够精确预测该类节点弯矩-转角关系的理论分析模型。实用而精确的弯矩和转角关系模型应具备以下特点：1)力学和数学理论基础；2)模型简单，参数较少且容易确定；3)与试验结果吻合良好，能够很好地解释节点的力学特性。

Ramberg-Osgood模型是常用的非线性模型，因为它形式简单，如式(1)所示。

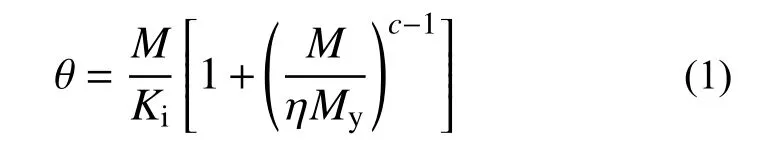
该模型考虑节点的转动刚度Ki、屈服抗弯承载力My、形状参数c以及引入考虑极限弯矩影响的形状系数η，通过选取适当的η和c，预测曲线和试验结果吻合较好。然而该模型不能明确定义节点的弹性阶段和极限状态[17]。

Yee等[15]提出钢结构中半刚性梁柱节点弯矩和转角关系的四参数指数模型，如式(2)所示，式中塑性抗弯承载力Mp，应变强化刚度Kp和初始转动刚度Ki均可通过模型计算，形状系数c通过试验数据回归得到，该模型参数较多且参数确定过程复杂。

在钢结构中节点的Kp/Ki不超过2%[24−25]，CFSTCEPBB的Ki大于钢结构节点，则CFSTCEPBB的Kp/Ki不超过2%。式(2)所示的模型中采用塑性抗弯承载力Mp，因此需引入应变强化刚度Kp来预测节点的极限状态，但确定Kp的过程复杂，增加预测弯矩-转角模型的工作量。研究表明对不同类型的节点采取适当的c值[15]，使得基于模型的预测结果精度更高，因此不应忽略形状系数c的影响。

基于以上分析，提出预测CFSTCEPBB弯矩-转角关系的三参数指数模型：

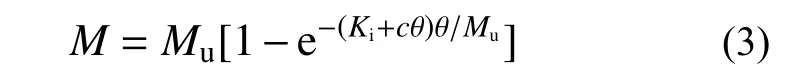
由于节点形式不同，极限弯矩Mu和初始刚度Ki不能通过已有的计算模型确定，将在下节提出适用于CFSTCEPBB极限弯矩的计算方法，建立初始刚度Ki分析模型。通过已有试验结果回归得到2种节点类型形状参数c的最优取值[8−10]，详情见表1。

表1 参数c取值Table 1 Value of parameter c

如图2所示，所提出的弯矩-转角关系模型满足以下4个特征：1)θ=0时，M=0，即曲线通过原点；2)θ=0时，dM/dθ=Ki，即曲线原点处的斜率等于节点的初始转动刚度；3)θ=θu时，M=Mu，即曲线通过极限状态点；4)θ=θu时，dM/dθ=0，即曲线在极限点处的斜率为0。

图2 弯矩-转角关系曲线示意图Fig.2 Schematic diagram of moment-rotation relation curve

2 节点极限弯矩计算方法

本节基于已有的钢结构螺栓端板连接节点[15]和钢管混凝土贯通螺栓端板连接节点的极限抗弯承载力分析模型[18]，提出CFSTCEPBB的极限弯矩计算方法。

Zhou等[18]提出钢管混凝土柱-钢梁端板贯通螺栓端板连接节点极限弯矩的计算方法为：

式中：hb为钢梁截面高度；tbf为钢梁翼缘厚度；F为节点破坏时钢梁翼缘拉、压力。F由以下5种破坏模式确定：1)端板受弯，Fep；2)螺栓受拉，Fbo；3)柱横向受压，Fc；4)核心区受剪，Fpz；5) 钢梁受弯，Fb；F=min(Fep,Fbo,Fc,Fpz,Fb)。

文献[18]中17个节点试件的研究结果表明，在节点破坏模式的预测结果和试验结果中均未出现钢管混凝土柱横向受压、核心区受剪的破坏模式；此外，Wang等[8−10]已对CFSTCEPBB进行试验研究，结果表明2种节点破坏时，钢管混凝土柱未出现明显的受压和剪切破坏。因此，为了方便实际工程应用，计算CFSTCEPBB的极限弯矩时不考虑钢管混凝土柱横向受压、核心区受剪2种破坏模式，仅考虑以下3种可能的破坏模式：1)端板受弯；2)螺栓受拉；3)钢梁受弯；如图3所示。根据常用的单边螺栓平齐式端板连接节点构造，假定：1)每排有2个螺栓；2)节点处的弯矩以钢梁翼缘中心处的轴力形式传递给柱。

图3 CFSTCEPBB的可能失效模式Fig.3 Possible failure modes of the CFSTCEPBB

基于以上分析，首先计算各破坏模式下钢梁翼缘拉、压力，然后通过式(4)得到各破坏模式下的极限弯矩，最终选取最小的极限弯矩作为2种CFSTCEPBB的极限弯矩，即：

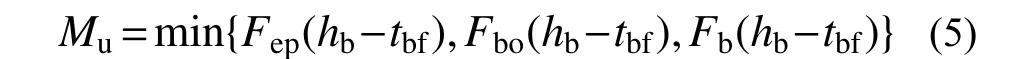
2.1 平齐式端板弯曲屈服破坏时钢梁翼缘的拉、压力F ep

CFSTCEPBB的钢梁和端板采用焊接连接，试验结果表明[8−10]，随着节点处荷载增大直至破坏，端板弯曲和螺栓拉伸幅度不断增大，但端板和钢梁的焊缝处均未出现撕裂现象，焊缝抗拉刚度远大于端板抗弯刚度。此外，对于贯通螺栓端板连接节点，未考虑焊缝影响，基于简化模型的预测结果和试验结果吻合很好[18,21]。因此，不考虑焊缝对节点性能的影响。当节点受弯矩作用时，翼缘力F通过焊接节点直接传递给端板。对于钢结构中通过平齐式端板螺栓连接的节点，端板抗弯承载力采用屈服线理论确定[26]，屈服模式如图4所示。

图4 平齐式端板屈服线模式Fig.4 Yield line mechanism of the flush endplate

CFSTCEPBB与钢结构梁柱节点仅柱形式不同，前者刚度较后者更大，使得端板能够更好的发挥抗弯能力。因此基于屈服线理论得到平齐式端板受弯屈服破坏时的钢梁翼缘力为[26]：

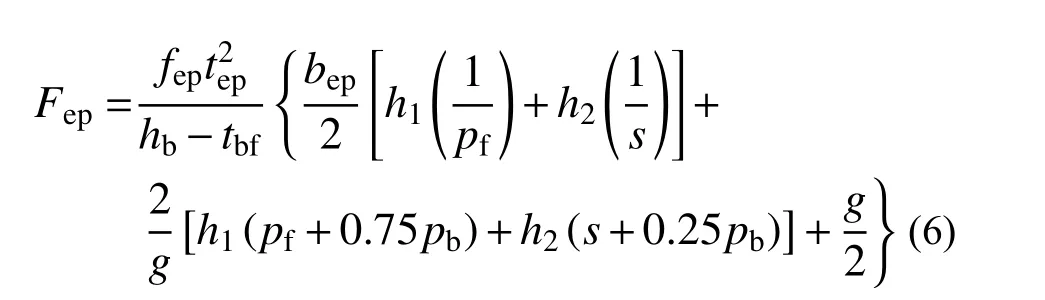
式中：fep是端板的屈服强度；tep是端板厚度；其他参数如图4所示。

2.2 螺栓受拉破坏时钢梁翼缘力F bo

梁柱节点采用平齐式端板和单边螺栓连接的钢管混凝土结构在遭受水平荷载作用时，钢梁承受水平力通过端板传递给螺栓，进而传递给钢管混凝土柱。当节点弯矩达到一定值时，受拉区端板会与柱壁分离，受拉区螺栓承受由钢梁翼缘拉力和撬力引起的轴向力。考虑撬力影响，螺栓受拉破坏时钢梁翼缘力为[20]：

式中：nt为受拉区螺栓数目；fbo,u和fep,u分别是螺栓和端板的极限抗拉强度；Abo是螺栓截面面积；dm是螺栓头的直径。

2.3 钢梁受弯屈服破坏时翼缘力F b

若钢管混凝土结构承受地震荷载时在框架柱内形成塑性铰，会引起整体结构破坏，造成大量经济和生命损失。为避免此类问题出现，在结构抗震设计时应使塑性铰出现在梁端，满足“强柱弱梁，强节点弱构件，强剪弱弯”的设计原则。

当钢梁受弯屈服时，由力学知识得钢梁翼缘力为：

式中：fb是钢梁屈服强度；Wz是钢梁弯曲截面系数，与横截面的形状和尺寸有关。

3 节点初始刚度分析模型

节点初始转动刚度是反映荷载初期节点变形能力的重要指标，目前确定半刚性节点的初始转动刚度通常采用试验或数值模拟的方法，消耗大量的人力物力，不具有实用性。因此，建立一种简便、实用且适用于CFSTCEPBB的初始转动刚度分析模型具有重要意义。组件法常被用来建立半刚性组合节点的初始转动刚度分析模型[21−23]，作如下假定：

1)各组件均处于弹性状态且为小变形；

2)仅考虑节点受拉区变形，忽略受压区变形；

3)节点的转动中心位于钢梁受压翼缘中心线处；

4)平截面假定。

节点受弯矩作用后变形如图5所示，由于受压区变形很小，可忽略受压区变形。节点转动主要由端板弯曲变形δep、螺栓受拉变形δbo和柱核心区剪切变形δc组成，根据小变形假设，节点转角为：

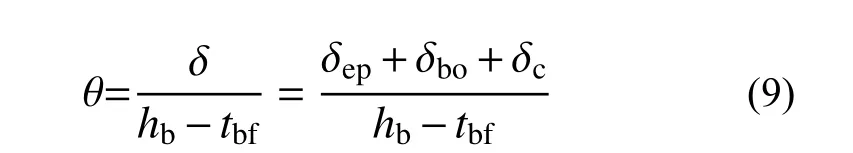
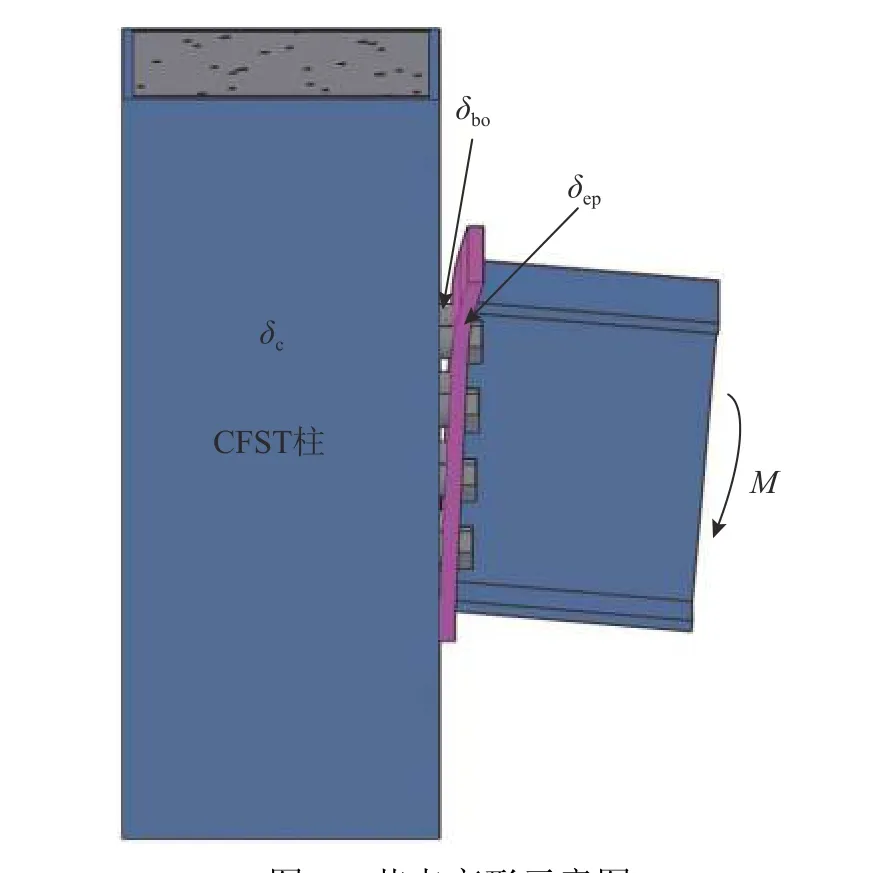
图5 节点变形示意图Fig.5 Schematic diagram for deformation of the CFSTCEPBB

根据材料力学知识，计算文献[8−10]中8个钢梁试件横截面翼缘对中性轴的惯性矩与腹板对中性轴的惯性矩之比，其值为5∶1～6∶1；此外，将梁端弯矩简化为作用于上、下翼缘的力偶，并未影响钢管混凝土柱与H型钢梁延伸端板贯通螺栓连接节点初始转动刚度模型的正确性[21]。因此，建立本文研究节点的初始刚度分析模型时，认为梁端弯矩主要由钢梁上、下翼缘承受，故可将节点处弯矩等效为作用于钢梁上、下翼缘处的力偶，如图4所示。则等效力大小为：

将CFSTCEPBB的端板、螺栓和柱核心区各部件简化为相应的等效弹簧，节点受拉区钢梁翼缘受等效力F作用时，各部件等效弹簧受力分别为Fep、Fbo和Fc，各弹簧变形分别为δep、δbo和δc，如图6所示。

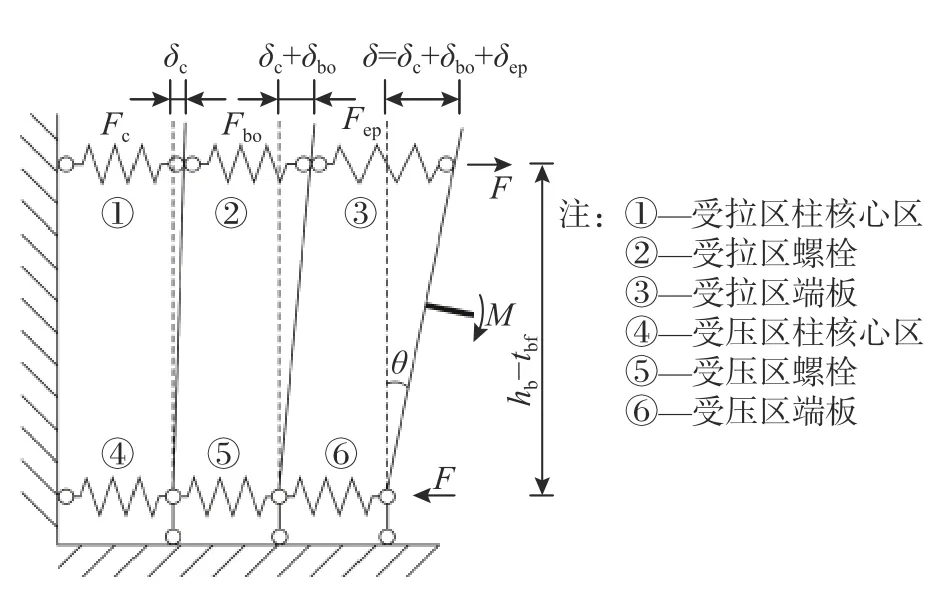
图6 节点等效弹簧变形图Fig.6 Deformation diagram of equivalent springs

根据胡克定律，各构件刚度为：

对节点处端板进行受力分析，如图7所示。端板与钢梁翼缘通过焊接连接，因此端板受钢梁翼缘传力为F，即Fep=F。由于端板处每根螺栓规格相同，且施加的预紧力相等，因此荷载初期受拉区每根螺栓对端板的压力T相等，由式(14)～式(15)确定。柱核心区受力仅由螺栓传递，故Fc=Fbo。由转动中心力矩平衡得：

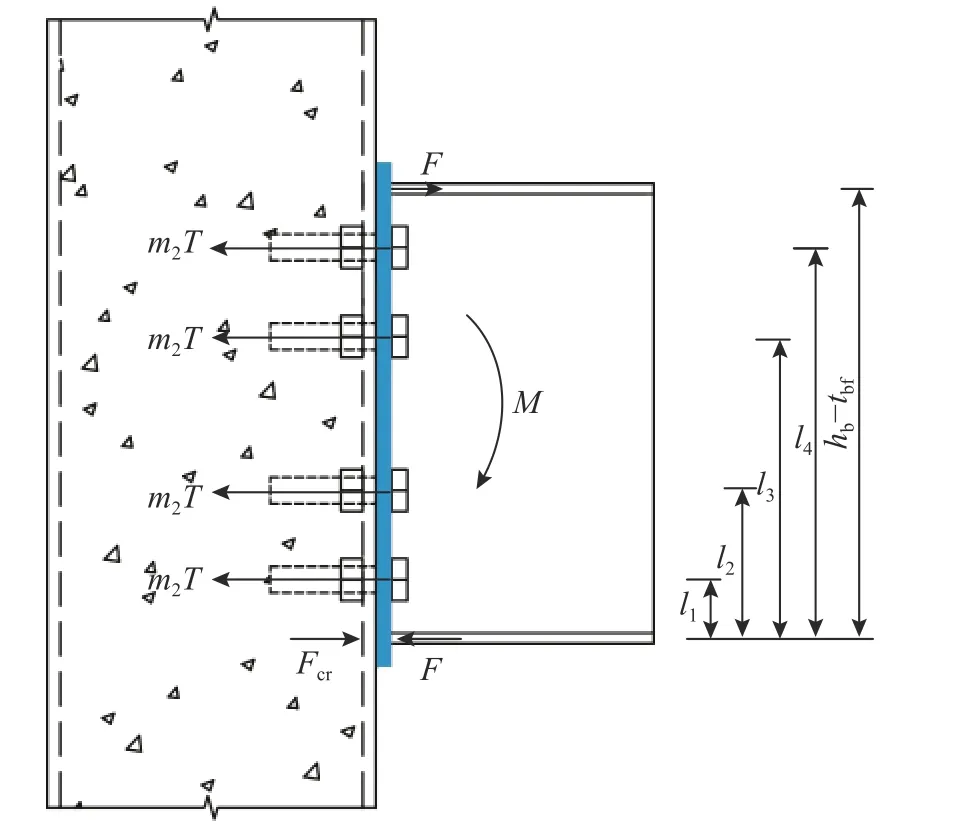
图7 平齐式端板受力图Fig.7 Forcesanalysisof theflush endplate

其中：

由式(14)～式(15)得：

式中：m2为每排螺栓数目；n为受拉螺栓数目。

由式(9)～式(16)得CFSTCEPBB的初始转动刚度为：

3.1 平齐式端板抗弯刚度K ep

端板受钢梁翼缘拉力变形如图8所示，端板通过螺栓预紧力与钢管柱壁紧密结合。荷载初期，由于对螺栓施加较大的预紧力，端板在螺栓处转动极小可忽略[22]，故可将平齐式端板受钢梁翼缘拉力简化为悬臂梁受集中荷载作用力学模型，如图8所示。

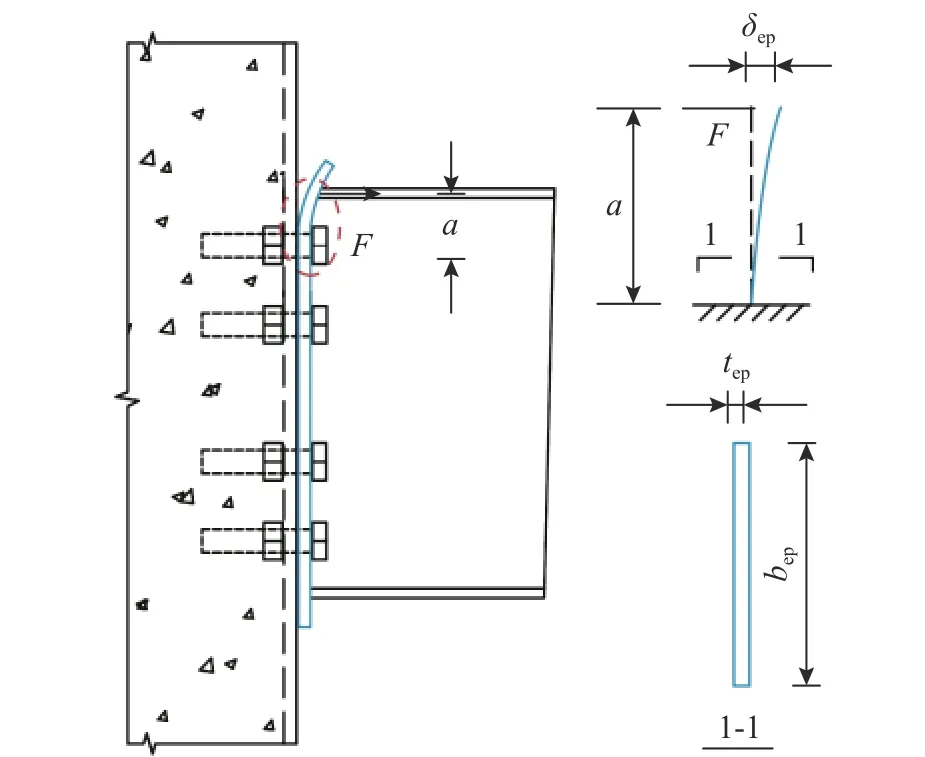
图8 平齐式端板受力简化模型Fig.8 Simplified mechanical model of the flush endplate

由力学知识得平齐式端板变形为：

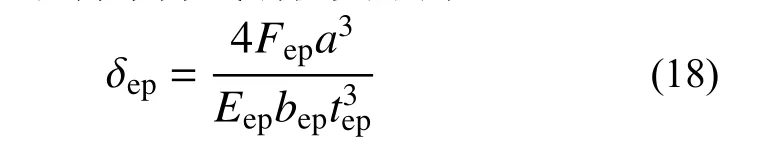
由式(11)和式(18)得CFSTCEPBB中平齐端板抗弯刚度为：

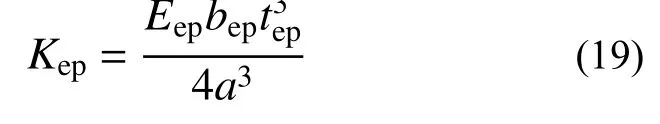
3.2 螺栓抗拉刚度K bo

计算端板抗弯刚度时，假定螺栓处为固定约束，端板在螺栓处无水平位移，然而螺栓受轴向外力作用会产生轴向变形，进而使端板产生水平位移，因此螺栓受拉变形是节点变形的重要组成部分。EC3[20]给出了螺栓轴向抗拉刚度为：

式中：0.8为考虑撬力的影响系数；Ebo为螺栓弹性模量；Abo为受拉螺栓有效截面面积；Lbo为螺栓穿过的有效长度。

有研究表明[22]撬力一般在外拉力达到预拉力50%时才开始出现，因此研究节点初始转动刚度时可不考虑撬力影响，故CFSTCEPBB中螺栓轴向抗拉刚度为：

3.3 柱核心区抗剪刚度K c

本文研究的节点类型采用单边螺栓，该类螺栓未穿过钢管混凝土柱的全截面。在螺栓拉力作用下，柱抗剪核心区的钢管柱腹板的剪切变形方向和钢管柱翼缘的弯曲变形方向均与混凝土剪切变形方向一致；此外，在小变形假定下，混凝土和钢管管壁无较大相对变形。因此，为简化节点初始刚度模型可不考虑混凝土和钢管管壁之间的相互作用。

在复式钢管混凝土柱-钢梁节点中紧固件采用单边螺栓[10]，如图9所示。由于混凝土硬化后对螺栓产生极大的握裹力[27]，螺栓拉力先作用于内层钢管柱单侧柱壁和夹层混凝土，进而传递给外层钢管柱壁。为使节点初始转动刚度理论计算结果偏于安全，假定荷载初期柱核心区有效抗剪截面面积如图9所示。其传力路径与普通钢管混凝土平齐式端板贯通螺栓连接节点相同，故将荷载初期复式钢管混凝土柱核心区抗剪简化为如图10所示的节点类型。

图9 复式钢管混凝土柱Fig.9 CFDSTcolumn

如图10所示，该类节点螺栓穿过柱全截面，荷载初期柱核心区变形可由钢管柱翼缘、腹板和核心混凝土三部分变形共同组成，以剪切变形为主[21]。因此，荷载初期柱核心区抗剪刚度由钢管柱翼缘抗弯刚度、钢管柱腹板抗剪刚度和核心混凝土抗剪刚度共同组成，根据不考虑受压区变形的基本假定，将柱核心区受力可简化为固定端短柱受力模型，如图10所示。

图10 复式钢管混凝土柱核心区抗剪简化力学模型Fig.10 Simplified mechanical model of CFSTcolumn in shear

柱节点核心区各抗剪部件受力和变形满足：

式中：Fcf、Fcw和Fcc分别为钢管柱翼缘、钢管柱腹板和核心混凝土受力；δcf、δcw和δcc分别为钢管柱翼缘、钢管柱腹板和核心混凝土变形。

由力学知识得各部件变形如下：

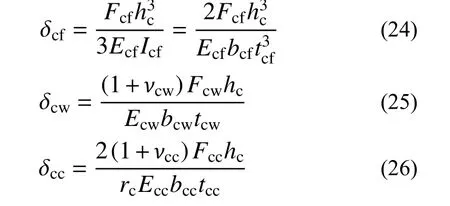
式中：Icf为钢管柱翼缘截面惯性矩；Ecw、Ecf、Ecc分别为钢管柱腹板、钢管柱翼缘、混凝土弹性模量；νcw、νcc分别为钢管柱腹板、混凝土泊松比；rc为考虑螺栓孔的混凝土抗剪刚度折减系数，按式(27)确定[28]；hc为柱核心区抗剪有效高度，按式(28)确定。

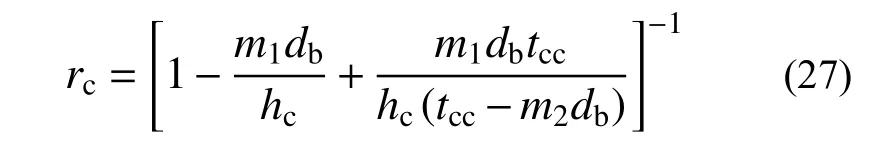
式中：tcc为柱核心混凝土厚度；m1为核心区螺栓排数；db为螺栓孔直径。

柱核心区受力主要由螺栓提供，螺栓传递拉力在钢管柱翼缘宽度方向沿45°扩散角传递[22]，因此柱核心区有效高度hc按下式确定：

式中：l1为受拉区最外排螺栓中心到钢梁受压翼缘中心的距离；af为螺栓中心到钢管柱翼缘边缘的距离，如图10所示。

由式(13)、式(22)～式(28)得CFSTCEPBB(复式钢管混凝土柱)柱核心区抗剪刚度为：

在普通钢管混凝土柱-钢梁节点中，核心混凝土抗拉强度低，混凝土硬化后的粘结效应会对螺栓产生极大握裹力[27]，螺栓没有穿过柱截面。荷载初期另一侧钢管柱翼缘和腹板不受螺栓拉力，因此不考虑核心区无螺栓部分混凝土、钢管柱腹板和另一侧翼缘对节点初始转动刚度的贡献。钢管柱角部对钢管柱翼缘平面外变形的约束与钢梁受压翼缘中心处对钢管柱翼缘的约束相比较小，同理将钢管柱翼缘受力作用简化为悬臂梁受集中荷载作用的力学模型，参与抗剪的混凝土简化为固定端短柱抗剪模型，如图11所示。

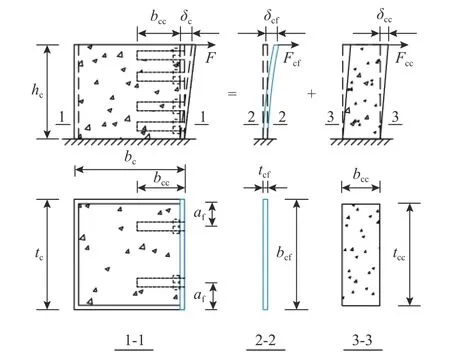
图11 普通钢管混凝土柱核心区简化力学模型Fig.11 Simplified mechanical model of ordinary CFST column in shear

钢管柱翼缘和混凝土受力分别为Fcf、Fcc，变形分别为δcf、δcc，满足：

该类节点仅考虑单侧钢管柱翼缘对柱核心区抗剪刚度的贡献，因此δcf为：

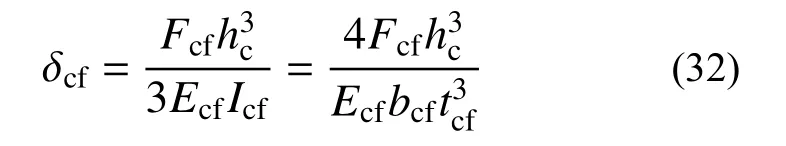
混凝土剪切变形计算同式(26)，由式(13)、式(26)、式(28)、式(30)～式(32)得普通钢管混凝土柱核心区抗剪刚度为：

4 模型正确性验证

4.1 极限弯矩和初始刚度计算模型

Wang等[8−10]对6个CFSTCEPBB试件进行了试验研究，试件端板形式为平齐式端板，螺栓为单边螺栓。其中试件SDSJ1-1和SDSJ1-2为复式钢管混凝土柱-钢梁节点，其余试件为普通钢管混凝土柱-钢梁节点。试件MTF1和MTF2采用单调加载方式；其余试件采用循环加载方式。

为了验证所提出的极限弯矩计算方法和初始刚度分析模型的正确性，基于本文研究结果得到每个试件极限弯矩和初始转动刚度的预测值，基于EC3[20]得到试件的初始转动刚度预测值，与试验结果进行对比结果见表2。所有试件的详细尺寸及试验详情见文献[8− 10]。

表2 计算结果和试验结果对比Table 2 Comparison of calculation results and test results

由表2可知，所有试件的预测破坏模式均为端板弯曲屈服破坏，各试件试验破坏结果如图12所示[8−10]，与本文对节点破坏模式的预测结果进行对比，结果表明基于本文极限弯矩计算方法对节点破坏模式的预测是合理的。

图12 试件试验破坏模式Fig.12 Failuremode of specimens in experiments

基于本文提出的极限弯矩计算方法的预测值与试验值之比的平均值为1.00，标准差为0.06，表明本文提出的极限弯矩计算方法适用于CFSTCEPBB，且预测误差很小。基于本文建立的初始转动刚度分析模型的预测结果和试验值之比的平均值为1.10，标准差为0.08；基于EC3的预测结果和试验值之比的平均值为0.62，标准差为0.37。因此本文提出的初始转动刚度计算模型能够准确地预测CFSTCEPBB的初始转动刚度，且与EC3的确定方法相比，预测精度有较大提高。

4.2 弯矩-转角关系模型验证

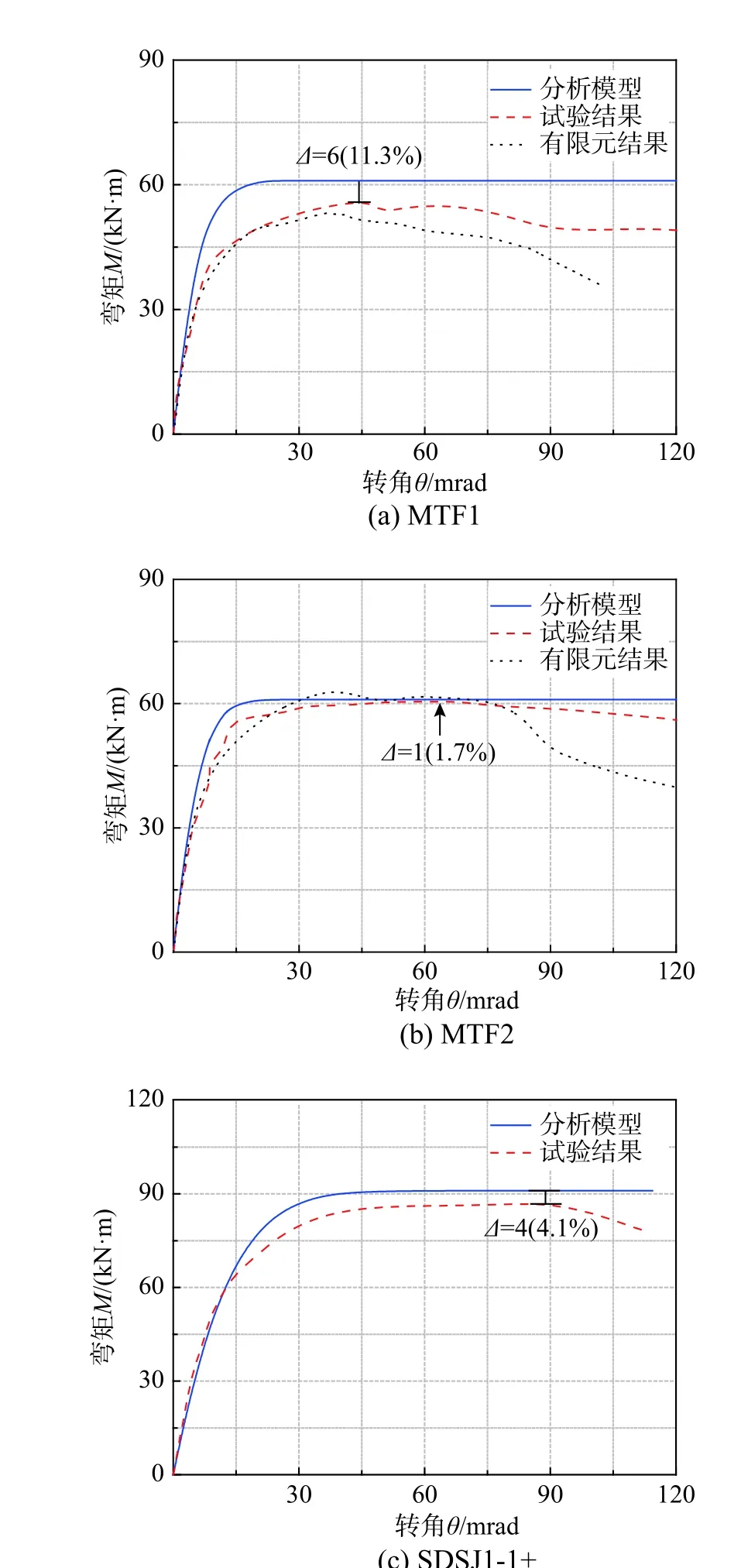
为了验证本文提出的弯矩-转角关系模型的正确性，基于模型得到试件的弯矩-转角预测曲线，与试验得到的弯矩-转角关系曲线[8−10]对比，结果如图13所示。

从图13的对比结果可见，基于本文提出的模型能够合理地预测试件的弯矩-转角关系曲线，预测曲线与试验曲线在弹性阶段基本吻合，主要差异在于对极限弯矩的预测，但误差较小。模型中的参数Ki和Mu分别在弹性阶段和塑性阶段具有特定的意义，因此本文提出的弯矩-转角模型能够适用于CFSTCEPBB的结构分析和设计。

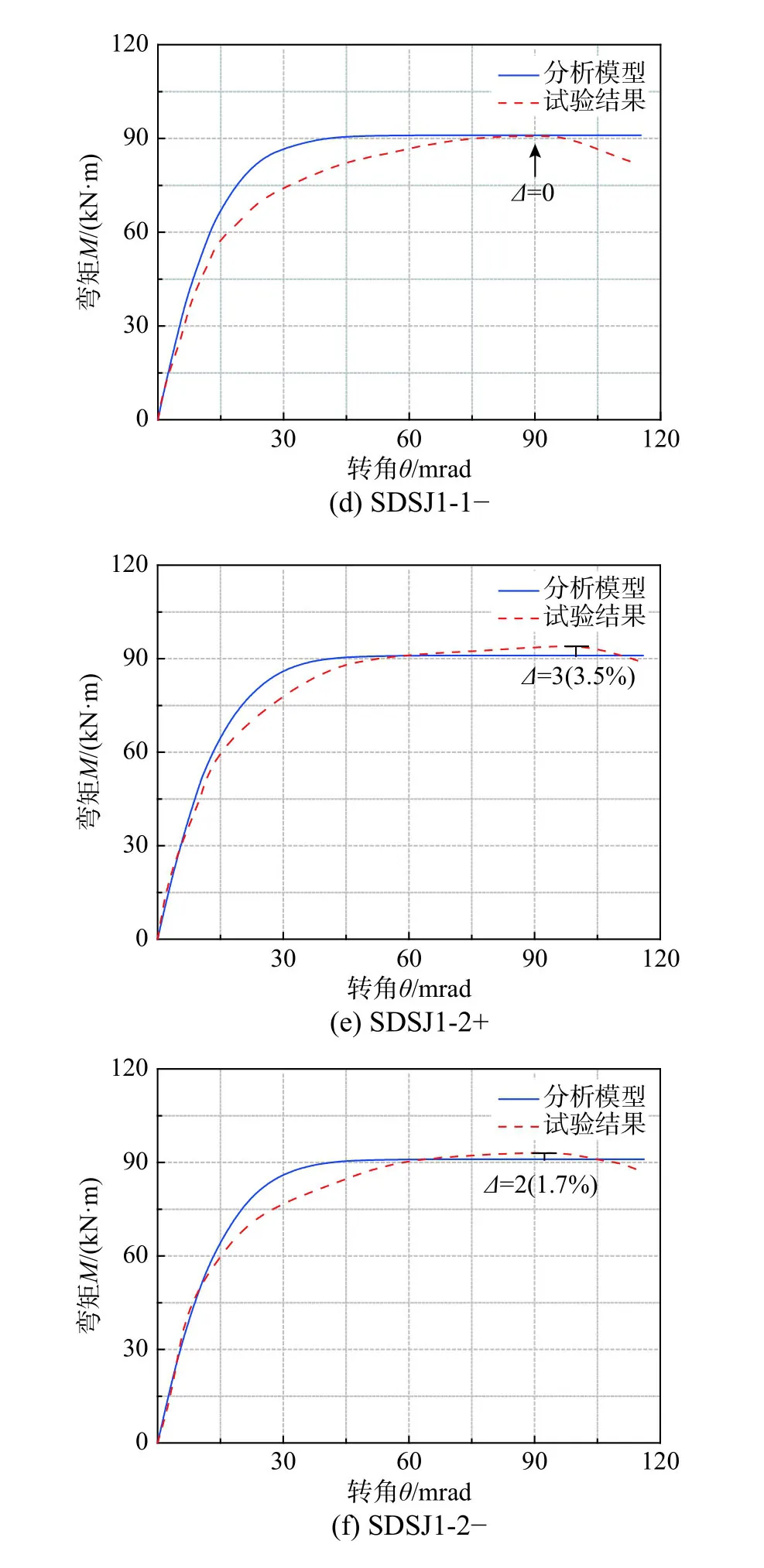
图13 弯矩-转角关系预测曲线与试验结果对比Fig.13 Comparison between prediction curves and test results of moment-rotation

4.3 数值模拟

通过ABAQUS6.14软件建立试件MTF1和MTF2[8]的有限元模型并进行分析。钢管柱、钢梁和端板的弹性模量、屈服强度和极限强度由试件的材性试验得到，螺栓采用10.9级高强螺栓；混凝土的相关材料参数根据立方体抗压强度试验结果确定。有限元模型中的钢材和混凝土本构关系分别采用强化的双折线模型和混凝土塑性损伤模型[29]。

有限元模型中钢管采用八节点线性六面体单元(C3D8R)和六节点三棱柱单元(C3D6)，其余钢材和混凝土均采用八节点线性六面体单元(C3D8R)。有限元模型及节点处网格划分详情如图14、图15所示。在相互作用设置中，钢材和混凝土之间、钢材之间的摩擦系数分别取0.6、0.3。

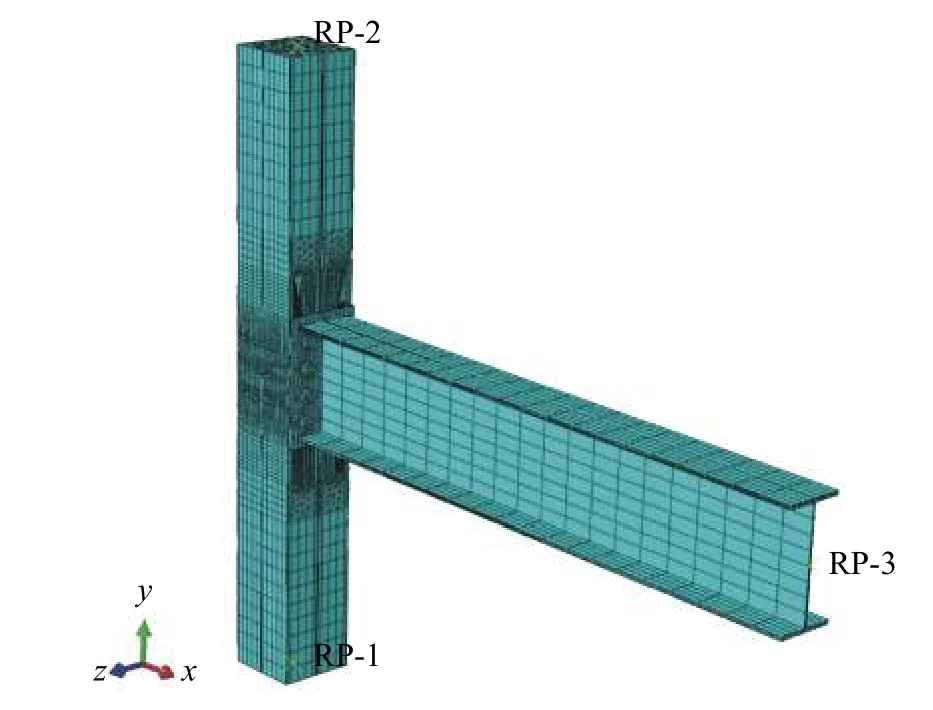
图14 节点有限元模型Fig.14 Finite element model of joints

图15 节点有限元模型网格划分Fig.15 Mesh generation of finite element model of joints

试件MTF1和试件MTF2的拟静力试验通过设置多个分析步实现，首先施加螺栓荷载，然后在钢管混凝土柱顶端施加与试验相同的竖向荷载，最后在梁端施加竖向单向荷载。其中，螺栓荷载分三步施加：步一，施加较小螺栓荷载；步二，施加螺栓实际预紧力；步三，固定螺栓当前长度。

通过有限元计算，得到节点试件MTF1和MTF2加载破坏后的变形和应力分布，如图16所示。有限元计算结果的节点破坏现象与图12(a)、图12(b)所示的试验破坏现象一致。此外，有限元分析所得节点的弯矩-转角关系曲线与试验弯矩-转角曲线和基于本文节点弯矩-转角关系模型的预测曲线在极限点之前吻合，如图13(a)、图13(b)所示。

图16 节点Mises应力分布及变形图Fig.16 Misesstressdistribution and deformation of joints

5 结论

本文对CFSTCEPBB的性能进行了理论分析，得到以下结论：

(1)建立预测2种CFSTCEPBB弯矩-转角关系的三参数指数模型(初始转动刚度Ki、极限弯矩Mu和形状参数c)，与试验结果对比表明该模型能够合理地预测节点的弯矩-转角曲线。此外，该模型参数少，且基于本文研究结果便于确定，可以灵活解决节点参数变化问题，便于在实际工程中应用。

(2)基于CFSTCEPBB的3种可能破坏模式，提出该类节点的极限弯矩计算方法，预测结果与试验结果之比的平均值为1.00，标准差为0.06，表明本文提出的极限弯矩计算方法的正确性。该计算方法中对节点破坏模式的预测与试验结果一致。

(3)基于组件法建立CFSTCEPBB的初始转动刚度计算模型，基于该模型的预测值与试验值之比的平均值为1.10，标准差为0.08；基于EC3的预测结果和试验值之比的平均值为0.62，标准差为0.37。对比结果表明本文提出的初始转动刚度计算模型的正确性，预测精度较EC3的方法有较大提高，且该模型中对柱核心区抗剪截面的假定是合理的。

(4)建立了试件MTF1和MTF2的有限元模型并分析，有限元计算结果中节点的破坏形态和试验现象一致，节点弯矩-转角曲线与试验曲线，基于本文节点弯矩-转角模型的预测曲线在极限点之前吻合，表明本文H型钢梁与钢管混凝土柱平齐式端板单边螺栓连接节点弯矩-转角分析模型的正确性。