光伏系统中ASI Boost变换器的稳定性分析与控制

顾志铭，周宇飞，熊向晖

(安徽大学电气工程与自动化学院，安徽合肥 230601)

在光伏系统中，常在光伏电池阵列与DC-AC 逆变器之间增加DC-DC 功率变换器，以提供稳定输出的直流电压[1]。Boost 等传统DC-DC 变换器在提高电压增益上能力有限，而开关电感(switched-inductor)单元和有源网络(active network)结构因其较高的电压增益、较小的开关管及二极管电压应力等优点在Boost 电路拓扑改进上得到广泛应用[2-3]。其中，适用于光伏系统前级变换器的有源开关电感(active switchedinductor，ASI)Boost 变换器[4]及其相关拓扑可以显著提高系统升压能力[5]。

光伏系统中的DC-DC 变换器属于强非线性系统，其内部参数的变化往往使变换器产生失稳现象[6-7]，通过建立变换器的离散模型，有利于揭开变换器失稳机理，对进一步采用控制方法使系统达到稳定具有重要作用。针对光伏系统变换器在峰值电流模式控制下因占空比大于0.5 产生的次谐波振荡和混沌现象，常用斜坡补偿法来拓宽稳定范围[8]，但往往造成平均输入电流下降、瞬态响应速度变慢等影响。基于参数共振微扰原理[9]，正弦信号经相位优化后可避免电流峰值偏离参考信号[10]。

本文对峰值电流模式控制下的有源开关电感Boost 变换器进行研究，分析电路参数变化对变换器工作性能的影响；设计了一种单周期复位积分网络产生的类正弦信号对系统进行优化控制，研究该控制方案在消除次谐波振荡和混沌现象、降低输入电流及输出电压纹波，提升瞬态响应性能等方面的有效性和可行性，使变换器工作性能得到改善。

1 光伏系统中有源开关电感Boost 变换器的工作原理和离散建模

1.1 有源开关电感Boost 变换器的工作原理

有源开关电感Boost变换器如图1所示。上下两组开关电感单元(左区域虚线)通过有源网络交错对称连接，4 个电感大小相等，设电感参数为L。假设电感电流处于连续工作模式，在每个时钟周期的开始时刻，时钟信号Clock 促使RS 锁存器置位，驱动所有开关管(S1、S2)导通，系统处于模态1，此时二极管D1、D2、D3、D4导通，D12、D34、D5截止，4个电感并联充电，电容向负载R供电，电感电流iL上升；当电流上升到参考电流iref时，锁存器复位，驱动所有开关管断开，系统处于模态2，此时D1、D2、D3、D4截止，D12、D34、D5导通，4个电感串联向电容和负载供电，在下个时钟信号到来之前，电感电流iL下降。

图1 有源开关电感Boost变换器

由变换器的工作原理可知电感电流上升速度m1和下降速度-m2分别为：

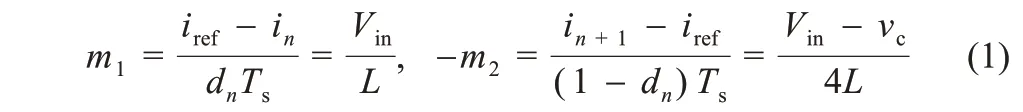
式中：dn为第n个时钟周期的占空比。由式(1)在一个时钟周期内电感伏秒平衡可知电压增益为：vc/Vin=(1+3dn)/(1-dn)，相比传统Boost 变换器，系统升压能力显著提升。

1.2 系统离散映射建模

因变换器4 个电感大小相等，基于变换器工作原理对系统进行降阶分析，其二阶微分方程：

其中状态矢量x=[iL，vc]T，系统矩阵为：

利用频闪映射法建立式(2)对应的离散迭代映射模型[11]。设xn=x(nTs)和xn+1=x[(n+1)Ts]分别为同一时钟周期开始时刻和结束时刻的状态变量，可得一个周期完整的离散模型：

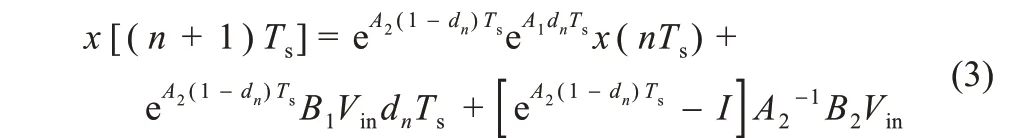
根据开关切换条件定义切换函数S3，其中K1=[-1，0]。

于是，式(3)和式(4)共同构成了有源开关电感Boost 变换器的离散映射模型。

2 光伏系统中有源开关电感Boost 变换器的失稳现象和稳定性分析

2.1 有源开关电感Boost 变换器的失稳现象

基于有源开关电感Boost 变换器的离散映射模型，在Simulink 搭建相应电路，选取参数：Vin=10 V，L=0.1 mH，C=100 μF，R=10 Ω，Ts=100 μs。定义Ib=iref-VinTs/L，它是时钟周期结束时电流iL刚好上升到iref，对应同一时钟周期开始时刻的电流iL数值。

以参考电流iref为变化参数的分岔图如图2(a)、(b)所示。可以看出，随着参考电流iref不断增大，当iref增大到11.9 A 时，系统因倍周期分岔失稳，由稳态进入周期二态；当iref继续增大到15 A 时，电感电流iL轨道与Ib(虚线)发生碰撞，系统从周期二态进入混沌。图2(c)、(d)对应参考电流分别为13 和25 A时，电感电流及电容电压的时域波形，可见系统失稳后电感电流和电容电压纹波较大，系统性能大幅下降。图3 为L和Vin为变化参数的电感电流分岔图，其参数变化使系统同样经历了倍周期分岔和混沌状态。

图2 iref为变化参数的分岔图及相应时域波形

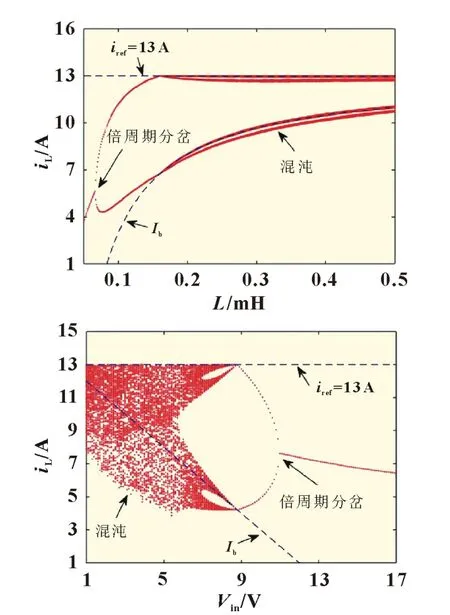
图3 L和Vin为变化参数的电感采样电流分岔图(iref=13 A)

2.2 稳定性分析

基于系统离散模型，令xn+1=xn=xQ，通过数值计算得到系统平衡点xQ。根据隐函数定理，在系统平衡点xQ处构造式(5)所示Jacobian 矩阵J，并代入det[λI-J]=0 中，求得对应的特征值λ。

通过数值计算求出图2 对应iref在5～12 A 变化时系统两个特征值的运动轨迹，如图4 所示。

图4 随iref变化的特征值运动轨迹

从图4 可以看出，当参考电流iref不断向11.9 A 增大时，其中特征值模|λ1|不断向1 靠近；当iref=11.9 A 时，|λ1|=1.001 1>1，此时系统失去稳定性，发生了倍周期分岔，从而验证了图2 的正确性。由此可见，电路参数的变化易使变换器失稳从而产生复杂的不稳定现象，因而需要对系统进行控制使其重回稳态。

3 稳定控制

针对传统斜坡补偿等控制的不足，基于参数共振微扰原理，本文设计一种易于实现且瞬态响应速度快的控制方案：将电感电流iL与可调基准稳态信号Ic的误差，利用图5(a)所示可复位开关的周期置零及电容充放电过程产生的类正弦信号对系统进行稳定控制，补偿信号is由图内虚线结构产生，图5(b)为对应is补偿波形，其数学表达式为：

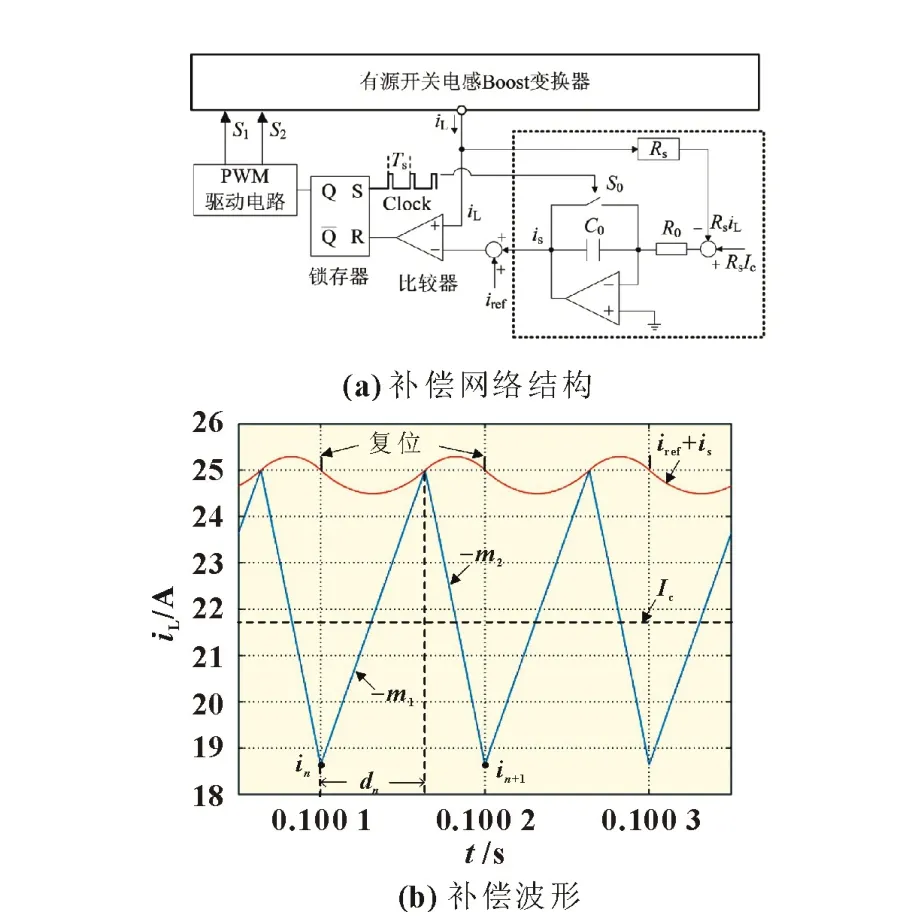
图5 单周期复位积分补偿

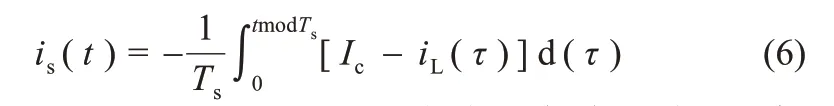
选取增益电阻Rs=1 Ω，R0C0=Ts。控制可复位开关S0在每个周期Ts开始时刻闭合，其余时间断开，补偿信号is在每个时钟周期开始时刻重置为零。考虑到变换器系统时间常数远大于时钟周期Ts，电容电压vc在一个周期内可看作近似恒定，由系统输入输出能量守恒可得：

假设变换器由模态1 向模态2 转换瞬间，电感电流iL峰值能达到参考电流iref，此时应有以下关系：

由式(8)解得Ic=iref-0.5m1dnTs。当系统处于准稳态时，可知Ic此时为电感稳态平均电流，根据补偿后的切换条件，将式(1)写成小扰动形式并只考虑瞬态变量，可得式(9)：

将Ic=iref-0.5m1dnTs代入式(10)后，λ=-1 和λ=+1 分别对应系统稳定下限和上限，因此可得系统稳定判据：

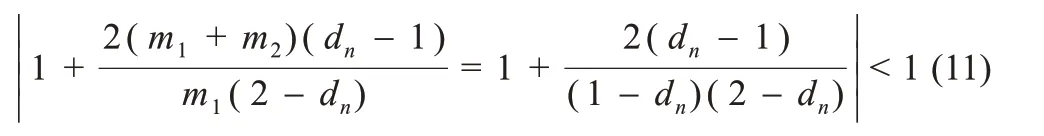
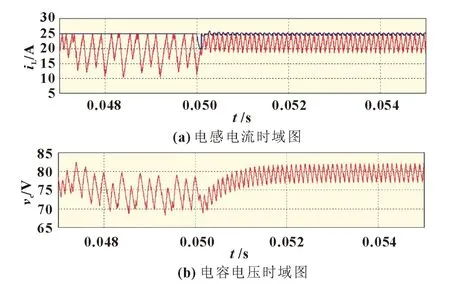
由0

于是，基于式(1)和式(7)求出iref对应的稳定占空比dn(0

图6 电路参数变化对稳态基准信号Ic的影响

4 仿真验证

为验证上述控制方案的有效性，以所绘图2 参数及参考电流iref=25 A 为例，在PSIM 搭建仿真模型，结合式(1)、式(7)和式(8)求得此时Ic=21.824 5 A。为更加直观地比较斜坡补偿、正弦补偿(相位优化后)和单周期复位积分补偿对系统性能的影响，在相同初始失稳条件下，t=0.05 s 时刻分别对系统施加上述前两种能满足稳定条件的最低控制强度的补偿信号(避免控制过强使电流与参考信号偏离过大)，并与加入单周期复位积分补偿后的控制效果进行比较，补偿前后的时域波形如图7、图8 所示。

图7 加入斜坡补偿、正弦补偿前后的电感电流时域图

图8 加入单周期复位积分补偿前后的电感电流和电容电压时域图

从图7可以看出，控制前的电流波形有着明显的不规则现象，电流纹波较大；在t=0.05 s 时刻加入斜坡补偿后，电流iL经过大约0.027 2 s由失稳达到稳定状态，但电流iL与参考信号偏离依然明显，以致电感平均输入电流较低；在t=0.05 s 时刻加入相位优化后的正弦补偿，系统稳定后的电流纹波降低且电流峰值与参考信号没有偏离，但瞬态响应速度仍然较为缓慢；相比于前两种补偿，从图8 可知在t=0.05 s 时刻加入单周期复位积分补偿后，电感电流峰值精确追踪参考信号且系统达到稳态更为迅速，电感电流和电容电压纹波降低，有效地提高了变换器的电压增益。表1 为三种控制方案在不同参考电流下仿真结果的性能比较，可以明显看到，单周期复位积分补偿在电感平均输入电流及控制时间等性能上更具优势。

表1 三种控制方案的性能比较

5 结论

基于有源开关电感Boost 变换器在峰值电流模式控制下的工作原理和离散映射模型，详细分析了电路参数对变换器稳定性的影响并揭示了系统失稳机理，针对斜坡补偿及正弦补偿的不足，设计了单周期复位积分补偿对系统进行优化控制。研究结果表明，此控制方案瞬态响应速度迅速，有效消除了系统次谐波振荡和混沌现象，电流峰值能精确追踪参考信号并有效降低了输入电流和输出电压纹波，对有源开关电感Boost 变换器的正确设计和稳定运行具有指导意义。