捕鱼策略优化SVR的城市需水量预测模型
郑 辉, 梁晓龙, 刘东岳
(石家庄职业技术学院 食品与药品工程系,河北 石家庄 050081)
随着城市化进程的加快,水资源逐渐成为制约城市发展的瓶颈.城市需水量的科学预测,有利于水资源优化配置,更好地发挥水资源效益.序列法、回归分析法等[1-2]的预测结果具有一定的波动性,且精度不高;灰色理论[3]在使用过程中需要构造大量的白化函数,工作量大,且普适性、通用性较差;BP(Back Propagation)神经网络法[4]不但存在容易陷入局部极值的问题,而且对BP神经网络隐节点个数的确定缺少理论依据.
支持向量机(SVR)模型[5-7]可以将复杂、高维的非线性问题映射到线性空间,用于解决高维、非线性、小样本的问题,模型在优化过程中具有收敛速度快,泛化能力强的特点.捕鱼策略优化算法是模拟渔夫捕鱼行为而提出的一种集群优化算法[8],具有搜索速度快,不易陷入局部极值,优化精度高的特点,在调度、管理、TSP(Traveling Salesman Problem)求解等方面有广泛的应用.
本文将捕鱼策略优化算法与SVR模型相结合,优化SVR模型参数,进行城市需水量预测,以期为优化水资源配置提供参考.
1 预测模型的构成
1.1 SVR模型
SVR模型的工作机理是:在线性可分空间中寻找一个分类超平面,在保证精度的前提下使待分类数据与超平面之间的空白区域最大化,SVR在理论上可以寻找到线性可分数据的分类超平面;引入核函数可以将线性不可分数据变换到多维线性空间,实现对线性不可分数据的线性分类.在此基础上引入Lagrange乘子法能将优化问题转化为线性方程组的求解问题,见公式(1).
(1)
简化得到的SVR模型(LS-SVR模型)表达式为:
(2)
在公式(1)、公式(2)中,b为待优化常量;αi为待优化支持向量;C为惩罚因子;k(xi,x)为内积核函数,一般选取径向基核函数,公式为:
(3)

1.2 捕鱼策略优化算法
渔夫在捕鱼时,总会自觉地向鱼密度更大的方向移动,移动过程中沿途捕鱼,发现鱼密度较大的位置,渔夫就会移到此处,以新的位置为中心重复撒网操作.
捕鱼策略优化算法有寻优撒网、收缩撒网和加速撒网三种.为了简化捕鱼策略优化算法,引入一个递减函数控制撒网半径,将加速撒网与收缩撒网融为一体,在搜索迭代中,撒网半径也会随之缩小,从而实现收缩撒网.捕鱼策略优化算法在解空间的搜索公式为:
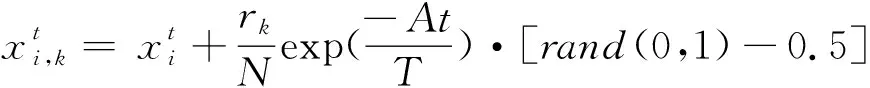
(k=1,2,…,p;i=1,2,…,N)
(4)
1.3 捕鱼策略优化算法的实现步骤
步骤一,初始化

步骤二,迭代搜索

步骤三,输出结果
当搜索到符合精度要求的解或者达到迭代阈值T(为避免陷入死循环而预先设定的数值)时,搜索停止,输出搜索到的最优解xi及最优解的适应度值f(xi);否则返回执行步骤二.算法的实现流程图见图1.
将捕鱼策略优化算法用于SVR城市需水量预测模型优化时,需要对捕鱼策略优化算法参数进行设置,经反复调试,各参数设置情况见表1.

表1 捕鱼策略优化算法的参数设置
2 捕鱼策略优化SVR的台州市需水量预测
2.1 台州市年总需水量影响因素及其归一化
影响总需水量的主要因素及其单位见表2.

表2 影响总需水量的因素及其单位
本文以台州市年总需水量[9]的拟合、预测为例.将各影响因素数值及年需水量数值用极差法进行归一化处理.为了提升模型的泛化能力,设置归一化因子收拢系数,对极差归一化公式中的最大值Zmax j和最小值Zmin j分别乘1.1和0.9的系数得到公式(5).
(5)
公式(5)中,Zmax j和Zmin j为所有样本中各因素j(或需水量y)的最大值和最小值.
经调整,各因素归一化数值均会向0.5有少量的靠拢.因此,在模型的预测中遇到略大于当前样本最大值Zmax j或略小于当前样本最小值Zmin j的数据时模型仍适用.台州市12年的年总需水量及7项主要影响因素数据见表3.

表3 台州市12年的需水量影响因素、实际用水量、拟合与预测值和相对误差数据
2.2 预测模型参数的优化
选取前9个年度序列(表3中1-9行)的台州市年需水量及其影响因素的归一化数据作为支持向量机的训练样本,用后3个年度序列(表3中10-12行)的数据作为模型的检验样本,检验SVR模型需水量的预测精度.各因素归一化数据见表4.

表4 样本各指标的归一化值和需水量的LS-SVR模型输出值
公式(2)中的参数C,σ,b,αi需要优化确定,本文采用捕鱼算法对其进行优化,目标函数公式为:
(6)
将目标函数公式(6)代入捕鱼策略优化算法中,对公式(2)中的αi,b,σ和C反复迭代优化.当迭代达次数达到迭代阈值T=10 000,目标函数值minQ=0.0036时,停止迭代,各输出参数的优化结果见表5.

表5 SVR模型参数优化结果
将优化得到的αi,b,σ和C代入公式(2),得到台州市年总需水量SVR预测模型的输出表达式为:
y=0.0441k1(x,x10)-0.5303k2(x,x20)+
0.4244k3(x,x30)+0.7387k4(x,x40)+
0.0472k5(x,x50)-0.8331k6(x,x60)+
0.1450k7(x,x70)+0.3203k8(x,x80)-
0.3563k9(x,x90)+0.4015
(7)
将表4所示需水量影响因素的归一化数据分别代入公式(7),再经归一化公式(5)的逆运算得出年总需水量的拟合值和预测值,并计算出相对误差值δi,结果见表3.由表3可以看出,台州市12年需水量的相对误差值均小于15%,其中有11年小于10%,6年小于5%,说明模型的拟合和预测精度相对较好.
3 结语
SVR模型优化速度快,泛化能力强,在解决高维度、小样本的非线性问题时具有明显优势.捕鱼策略优化算法具有多参数优化能力,不易陷入局部极值,可以使模型更精确.对台州市需水量的拟合、预测实例证明,该模型的拟合、预测精度均较高,既可以为水资源管理提供科学依据,也可以为其他预测模型的研究提供参考.

