基于LSTM+MIDAS深度学习模型的电力需求预测

洪小林

(河海大学 理学院，江苏 南京 210098)

电力需求预测是智能电网的重要组成部分。通过应用智能电网系统可以有效地管理电能并提高经济效益，智能电网中的电能调度管理要求预测不同设施的电力需求。电力需求波动性评估与智能需求响应相互作用，实时监测电能并管理电能需求[1]。预测电能使用量以确保充足的电能供应与提高电能效率密切相关，准确预测电能需求可以减少能源浪费，提高能源利用的可持续性。

文献[2]使用支持向量机(SVM)和用电数据对电力需求进行了预测。然而，仅使用机器学习算法无法识别特定时区的变化，因此仅从历史用电数据很难准确预测电力需求。文献[3]通过预测每个时区电力需求波动来提高准确性。同时，电力需求预测系统还需进行数据采集、预处理、特征提取等各个环节，因此电力需求预测系统需要耗费大量的时间和计算[4]。由于每个用电设施都有各自的使用模式，而且用电量、详细用电量和额定容量各不相同[5]，因此，还需通过深度学习对电力需求波动性进行分析。文献[6]按季节、日、月和小时对数据进行分析后发现电力需求的波动模式。

本文基于深度学习对每个用电设施进行了电力需求预测，以长短期记忆网络(LSTM)深度学习方法为基础，利用混合数据抽样(MIDAS)方法对自回归分布滞后(ARDL)进行改进，提出了LSTM+MIDAS模型的电力需求预测方法。通过收集住宅、工厂、医院和市政厅等4个设施的电力需求来计算每种电力需求使用模式的预测精度。该模型能够与实际使用情况相比较以此确定不合格的波动性，并提供高精度的预测结果，通过数值计算估计影响电力需求的不同数据形式。

1 ARDL方法与MIDAS逼近法

1.1 ARDL方法

ARDL利用分析时间序列数据的动态回归分析，可实现预测电力需求误差修正和协整。在电力需求预测中，ARDL方法假设月电力需求影响几年前的电力需求并包含自回归阶数，采暖度日和降温度日包含在上月的自变量中。统计显著性水平可以根据使用情况采用不同的模型来确定。因此，从周数据(xt)可以预测第t月第j周的月数据(yt)，则因变量Ay和自变量Ax的自回归度ARDL(Ay，Ax)模型为：

(1)

式中，μ为固定参数；αi和βj分别为月数据和周数据的系数；ut为滞后项。

假设月份固定为4周：j=1，2，3，4。由于用电需求的特点，电力需求预测对温度和季节因素非常敏感，历史数据越早，对预测数据的影响就越小[7]。因此，应为每个历史数据分配不同的权重，进而更准确地预测电力需求[8]。如果为式(1)中的周数据赋予不同的权重，则可以导出：

(2)

式中，a为固定参数；w为1周；bt为滞后项；βw，t-j为权重为w的周数据xw，t-j的系数。

利用式(2)计算ARDL(1，2)时，x的估计系数数量为8(2×4)。本文中使用的数据是日数据，因此假设每月30 d，则估计系数数量为60(2×30)。在这种情况下，由于自由度损失，模型本身的估计变得困难，结果的可靠性也很低。

1.2 MIDAS逼近法

与ARDL方法类似，使用MIDAS方法的电力需求预测系统通过回归模型对用电需求进行预测。MIDAS最大的优点是权重函数自动分配：

(3)

式中，θ为权重函数的参数向量；Nw为周数；Dy和Dx分别为每月和每周的天数。

式(3)中的MIDAS与式(1)中的ARDL相似，但包含函数φ(j；θ)，该函数对高频(滞后)施加不同的权重[9]。因此，当通过MIDAS逼近法预测电力需求时，可以通过考虑电力需求数据之外的各种外部因素来进行预测，而无需调整权重函数的参数。

为了根据频率分配不同的权重，采用MIDAS方法中的权重函数，通过将温度、工作日数设置为自变量，可以提高短期电力需求预测的准确性[10]。周六设置为半天，不包括节假日和周日，并将工作日数相加[11]。另外，由于可以通过分离工作日和周末电力需求数据来分析电力需求的波动模式。因此，可以在工作日和周末之间电力需求差异较大的设施进行预测。

2 数据集处理

2.1 模型框架

本文的数据集和LSTM电力需求预测模型框架结构，如图1所示。

图1 预测方法的框架结构

为了识别预测模式，本文将数据分为短期数据和长期数据。根据电力需求，通过收集每个设施的数据进行实验。通过测量3种实验方法的预测误差率，对不同时期(短期和长期)的数据来评估预测模型：①现有的电力需求预测MIDAS算法；②现有的LSTM模型；③本文提出的LSTM+MIDAS模型。利用这3种方法对短期数据和长期数据进行实验，从而比较预测精度的差异。对于具有较大变化电力需求模式的住宅设施，还需从季节、天气和假日等方面进行分析。最后，本文将LSTM+MIDAS模型的性能与其他现有研究进行比较。

不同设施的平均最大电力需求数据集如图2所示。

图2 不同设施的平均最大电力需求

在图2中，以住宅和市政厅为例，夏季(6月—8月)平均最大电力需求呈上升趋势，但市政厅平均最大电力需求较高，并且冬季(11月至次年1月)与夏季无差异。虽然各设施的电力需求差异较大，但工厂的平均最大电力需求最为相似，每年的用电量在600～700 kWh。医院的最大用电需求在4个设施中最高，在5月—9月气温上升期间，表现出最高的电力需求。然而，住宅在夏季和冬季的最大电力需求差异最大，在除夏季以外的其他季节中，最大电力需求表现出相似的模式。因此，本文对住宅的季节性电力需求预测进行进一步的实验。

2.2 数据集

2019年11月至2020年10月，通过安装在各类设施(住宅、医院、市政厅、工厂)的电力计量传感器收集电力需求。利用住宅、工厂、医院和市政厅等4个设施的电力需求来计算每种电力需求使用模式的预测精度。收集用电数据以每天5 min的频率共收集288个数据组成。数据集的输入和输出见表1。

表1 数据集的输入和输出

使用表1中的不同数据成分进行短期、长期和季节性预测。根据季节特征，将冬季划分为2019年11月至2020年1月，夏季为2020年6月—8月。

利用表1给出了输入和输出数据集的结构，在LSTM模块中，输入的训练数据与测试数据的比例为2∶1。由于一周中每天的电力需求模式相似，输入数据(训练数据和测试数据)和输出数据由同一天(7 d滞后)数据组成。在短期预测中，利用前3周的3个7 d滞后数据来预测下一周同一天的数据。在长期预测中，利用前12周的12个7 d滞后数据来预测未来4周内同一天的数据。例如，在预测未来4周内每周一的电力需求数据时，将前12周的数据用作训练数据和测试数据。同样，在季节性数据预测中，用前9周的7 d滞后数据来预测未来3周。根据3个模型的输入和输出数据提出的LSTM结构流程如图3所示。

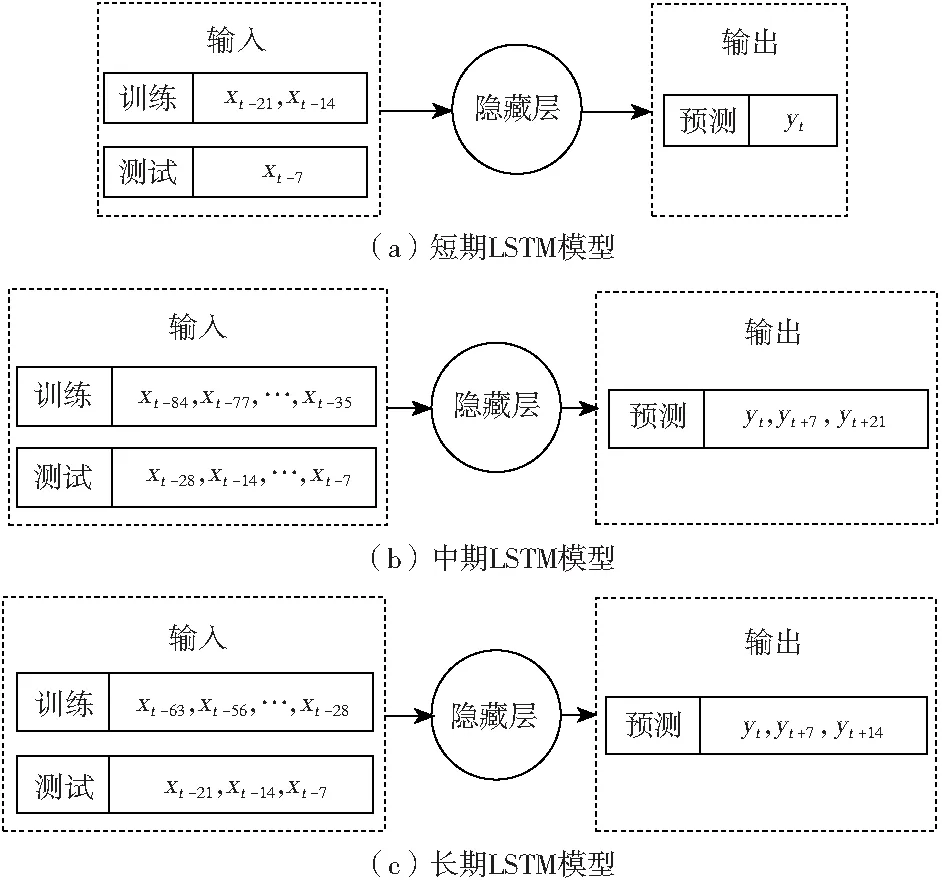
图3 各LSTM模型流程

2.3 数据预处理

在LSTM+MIDAS电力需求预测模型中，输入电力需求作为输入数据之前，通过对影响预测数据波动性的输入数据赋予不同的权重进行预处理。因此，使用MIDAS逼近法的权重函数对每天输入的数据进行加权，类似于预测的波动性。

(4)

利用式(4)对数据进行预处理：

(5)

式(4)为ALMOD指数函数，主要用作MIDAS回归方法的加权函数[12]。其中，θ为权重函数的参数向量。权重函数的形状和速度取决于θ值，为了实现权重的指数增加，将θ值设置在-0.002～0.010。W为W(n；θ)的向量矩阵；b为偏差系数。如果加权计算后的值与原始数据相差太大，则通过调整偏差值进行调整，偏差在-0.03～4.25。

3 基于LSTM的电力需求预测模型

3.1 LSTM+MIDAS模型

考虑到电力需求的波动性，本文采用能够反映现有MIDAS中使用的权重函数值来建立适合于时间序列预测的LSTM模型。使用的LSTM+MIDAS电力需求模型的结构如图4所示。

图4 LSTM+MIDAS模型的结构

在LSTM+MIDAS模型中，输入层的输入数据作为参数输入到输入门、遗忘门和输出门中。输入参数值通过计算权重和偏差值输入。在每个门处，根据时间计算不同的值。图4的LSTM结构如下：

(6)

(7)

(8)

(9)

(10)

(11)

3.2 每个模型的评估比较

为了评估LSTM模型的预测性能，本文使用平均绝对百分比误差(MAPE)、均方根误差(RMSE)和R2来测量统计分析。每个模型的评估公式如下：

(12)

(13)

(14)

R2的正常范围为[0，1]，并且越接近1，模型的预测能力越强[13]。由于本文中使用的电力需求数据在规模上因设施而异，因此计算R2来比较根据设施预测的结果。

3.3 训练环境

由于深度学习4J(DL4J)适合基于深度学习的时间序列数据预测，因此，本文使用DL4J构建基于LSTM的电力需求预测模型。DL4J的特点是易于构建可以使用图形处理单元(GPU)的环境。本文提出了一种基于DL4J方法和MIDAS相结合的LSTM模型，并用于电力需求预测的优化。

4 实验分析

4.1 参数设置

通过设置合适的参数可以获得良好的深度学习性能。根据数据的数量或目的来寻找最优的参数设置，如，最佳层数、节点数、迭代次数、激活函数等参数设置，在参数设置中总共进行了40次设置，得到了最优的结果。本文将隐藏层数设置为3，节点数设置为10，学习速率设置为0.01，并将迭代次数设置为180。采用双曲正切(tanh)和随机梯度下降分别作为LSTM层的激活函数和优化算法。在分类LSTM模型中，交叉熵(CE)和误差平方和(SSE)作为多类别分类进行预测的成本函数，但均方误差(MSE)主要用于对回归进行预测[14]。因此，本文使用MSE作为代价函数来降低预测误差。LSTM+MIDAS模型的参数设置值见表2。

表2 LSTM+MIDAS模型的参数设置值

由表2可见，寻找优化参数实验中获得最高准确率的3个结果。根据不同的设置显示出不同的预测结果，本文使用具有最高精度的设置3。

4.2 实验结果比较

短期预测结果见表3，长期预测结果见表4。在短期预测情况中，住宅、市政厅、工厂、医院用电需求预测的MAPE分别从21.04%下降到10.44%，从15.6%下降到2.73%，从7.21%下降到1.63%，从7.1%下降到1.96%。在长期预测情况中，不同预测方法的误差率无显著性差异。

表3 短期预测结果的误差率

表4 长期预测结果的误差率

住宅的季节性用电需求预测结果见表5。

表5 住宅季节性用电需求预测结果的误差率

由表5可见，与表3和表4中的短期和长期预测结果不同，在季节性用电需求预测实验中，不同预测方法表现出的误差率差异较大。在冬季实验中，预测的数据包括假期，这大大减少了电力需求。因此，在MIDAS方法中，本文给假日数据赋予更大的权重。但是，在LSTM方法中，未分配权重值，因此LSTM的性能最低。

4.3 统计结果

本文使用Friedman检验作为非参数统计检验，将LSTM+MIDAS模型与其他2种方法(LSTM、MIDAS)的短期、长期和季节性试验结果进行比较[15]。Friedman检验通常形式是使用秩而不是原始值，其中秩是通过分别对行进行彼此独立的排序而获得。所有预测MAPE结果的Friedman检验结果如下：总体MAPE结果(短期、长期和季节性)数量N为10；卡方为8.6；自由度(DF)为2；p值为0.018。Friedman的临界值设置为0.05的显著性水平。

4.4 性能分析

本文提出了LSTM+MIDAS混合模型只需使用历史电力需求数据的短期数据优化电力需求预测模型。电力需求预测的准确性取决于数据预处理和权重函数。此外，建立一个能够密切跟踪电力需求随时间变化的波动模式。在表4中，证实了LSTM+MIDAS模型比其他2种方法能够更好地反映电力需求波动。

综上所述，本文确定了住宅设施的预测性能最低，而工厂和医院设施的预测精度较高，且误差率相对较低。短期数据的LSTM+MIDAS模型的预测水平高于其他2种方法。同时，短期数据的结果也相对好于长期数据。与短期预测的最大MAPE相比，LSTM+MIDAS模型在住宅设施减少10.44%，市政厅下降12.87%，工厂下降5.58%，医院下降5.14%；在长期预测的情况下，住宅设施只下降了2.11%，市政厅下降了2.8%。长期预测并没有改善工厂和医院设施电力需求预测的错误率。利用短期数据进行电力需求预测更准确地反映电力需求的波动性，从而提高短期预测的准确性。然而，长期数据的预测受天气和外部因素的影响较大。因此，尽管由于数据集数量较多，总体精度较高，但该方法的精度没有太大差异。在长期电力需求预测中，预测的准确度并没有提高。由于电力需求数据与波动性相关，在波动趋势出现时，长期电力需求数据不能很好地预测。对受天气、季节和假日影响的住宅设施的电力需求预测，通过考虑特殊情况的权重对数据进行季节分类和预测，从而获得更高的精度。以6 h为间隔的3 d内住宅季节性电力需求预测如图5所示。

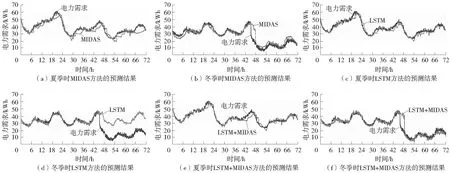
图5 以6 h为间隔的3 d内住宅季节性电力需求预测

该文将7月份的数据用于夏季预测，将夏季的住宅用电需求预测结果与文献[16]的LSTM预测结果进行了比较。本文提出的LSTM+MIDAS模型的MAPE为5.400%，LSTM模型的MAPE为8.935%。与LSTM相比，LSTM+MIDAS的误差率(MAPE)降低了39.564%。此外，通过Friedman检验，LSTM+MIDAS模型小于a(p<0.05)。因此，通过Friedman检验，LSTM+MIDAS模型的结果具有统计学显著性。

5 结论

本文提出了LSTM+MIDAS电力需求预测模型，只需利用历史电力需求的短期数据即可对电力需求进行预测模型。通过收集住宅、工厂、医院和市政厅等4个设施的电力需求来计算每种电力需求使用模式的预测精度，以较低的错误率预测电力需求。住宅受季节因素的影响较大。由于只考虑电力需求数据作为输入数据，住宅设施受天气影响的预测误差率比其他设施有所增加。同时，该模型能够确定不合格的波动性，并提供高精度的预测结果。