短期电力负荷预测的时间序列数据深度挖掘模型设计
董 亮,阚新生,邓国如,徐 杰,袁 慧
(1.国网湖北省电力有限公司信息通信公司,湖北 武汉 430077;2.中国联合网络通信有限公司武汉市分公司,湖北 武汉 430000)
短期电力负荷预测对于短期电力负荷预测水平的提高,可以帮助电力局提高电力管理水平,降低发电成本,可以为电力的管理和规划提供重要的管理依据[1]。而数据深度挖掘对于提取隐藏的数据信息和潜在有用的知识,并广泛用于各个企业,且取得了良好的经济效益[2]。因此,国内外众多研究者,都在短期电力负荷预测这一领域中,应用数据挖掘技术,并做了大量工作。尤其是近年来,国内外已经将人工智能技术,应用在对电力负荷预测中的数据挖掘技术中,如粗糙集、神经网络、Petri网等[3]。数据挖掘技术始于20世纪80年代末,且对于数据挖掘技术并未得到相应的重视,却在此后的时间里,快速发展数据挖掘技术,并将数据挖掘技术,与人工智能、数据库、机器学习等领域紧密结合[4]。随着对数据挖掘技术的开发,除国内外的研究学者外,各企业也开始加入数据挖掘研究的领域,并将数据挖掘技术进行细致的划分,如数据模型、数据类型、数据应用等[5]。文献[6]提出基于划分法的数据挖掘模型,预测短期电力负荷;文献[7]则提出基于层次法的数据挖掘模型,预测短期电力负荷。但是在上述的研究中,数据挖掘技术在预测短期电力负荷时,短期电力负荷预测存在数据时间序列紊乱现象,导致预测短期电力负荷精确度低,为此研究用于短期电力负荷预测的时间序列数据深度挖掘模型。
1 设计时间序列数据深度挖掘模型
1.1 数据预处理
采用时间序列数据深度挖掘技术,建立时间序列数据深度挖掘模型,预测短期电力负荷,需要促使此次建立的模型,具有数据预处理能力,可以在大量的电力数据信息中,提取预测短期电力负荷的数据,并对提取出的数据进行预处理,从而减轻时间序列数据深度挖掘模型,在预测短期电力负荷时的计算量。因此构建数据仓库体系,对电力数据进行预处理,其电力数据仓库体系结构如图1所示。

图1 数据预处理电力数据仓库体系结构
从图1中可以看出,此次对电力数据预处理而设计的电力数据仓库体系,分为数据源的数据获取层,数据抽取、转化和装载的数据处理层,操作型数据存储、中心数据仓库、数据集市、多维数据集等组成的数据存储层和用户访问分析的数据访问层。
在数据获取层,针对源数据的获取,在此次设计电力数据仓库体系,为降低数据处理步骤,根据数据来源,划分为相关数据、电力数据、历史数据和外部数据4个方面,根据不同的来源,对获取的电力数据,根据数据仓库的要求进行提取;清洗其中存在的错误数据或者填补其中缺少的数据,确保数据的完整性后;将数据转换成统一数据类型,保证数据格式的统一;此时,数据中会存在许多细节数据,需要对数据进行集成处理;经过上述的提取、清洗、转换、集成处理后,自动加载处理好的电力数据,完成合格数据入库过程[8]。
此时数据仓库中,所含有的数据信息包含电力体系的所有数据信息,并完成数据存储循环,促使电力数据存储层中的数据,与电力公司数据具有一致性,可以实时通过数据访问层,对数据信息进行访问,直接统计数据,挖掘数据中存在的相关性。
1.2 划分数据时间序列
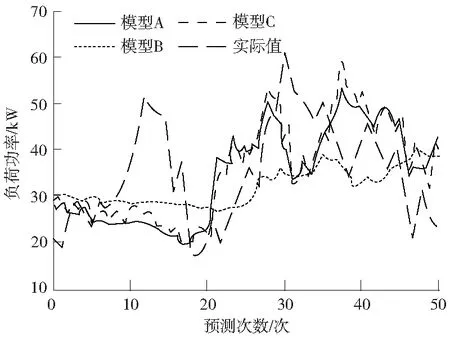
由图1电力数据仓库体系处理后得到的数据,进行数据时间序列划分,从而根据历史数据对短期电力负荷进行预测。因此,将通过数据访问层,提取数据存储层中的数据信息,将其中的数据数量设为n,其具有的时间序列为T,且T=〈t1,t2,…,ti,…,tn〉,其中i表示第i个数据,根据时间序列T设定的数据先后关系,将其时间序列的分界点数量设为K,当时间序列T具有K+1个分界点,设时间序列T的分界点为b,即当〈tb1,tb2,…,tbi,…,tbk+1〉(1=b1 在如图2所示的时间数据序列3种模式图中,设2个数据之间的相邻距离为l,则其相邻采样点为ti-l、ti和ti+l,其距离阈值为d,且d>0。此时,针对图中跳跃、渐变和尖峰3个模式,进行数学定义。跳跃模式时,2个数据之间的距离阈值为|ti+l-ti|≥d,其中ti-l 图2 时间数据序列3种模式 (1) 式中,Nt表示子序列Si中包含的数据个数。此时即完成数据时间序列的划分,但是在分割的过程中存在数据分割界限模糊问题,为了进一步提高数据划分质量,设子序列Si中的数据信息为标准数据信息。则可以将子序列Si中所有数据点的特征Fi定义为: Fi=(bi,Ni,Li,Ui) (2) 此时,根据式(1)和式(2),令子序列Sj中所有数据点的特征Fj=(bj,Nj,Lj,Uj),其中j表示第j个数据,将子序列Si和子序列Sj所有数据点特征合并为Sm,则Sm数据点的特征Fm为: Fm=(bm,Nm,Lm,Um) (3) 此时,式(3)的Fm等于Fi加Fj之和。因此,子序列Si和子序列Sj所有数据点特征合并序列Sm的第1个数据为bm=min(bi,bj),即是Si和Sj中的最小起点数据;个数和为Nm=Ni+Nj;则其数据点的线性和、有数据点的平方和为: (4) 综合式(1)、式(3)和式(4),即完成数据时间序列的划分。根据划分好的时间序列,综合电力数据仓库体系,即可构建实践序列数据深度挖掘模型,预测短期电力负荷。 综合1.1和1.2设计的数据处理电力数据仓库体系以及划分的数据时间序列,设计时间序列数据深度挖掘模型,预测短期电力负荷,其时间序列数据深度挖掘模型建模过程,如图3所示。 图3 时间序列数据深度挖掘模型建模过程 基于1.2设置的原始数据时间序列T=〈t1,t2,…,ti,…,tn〉,建立如图3所示的数据累加,则有: (5) 式中,T(1)为累加后的数据。此时的T(1)(k)为数据累加值[13]。 建立微分方程,则有: T(k)+az(1)(k)=c (6) 式中,a为发展系数;c为方程作用量;z为累加值参数[14]。 此时,根据式(6),计算微分方程的背景值,则有: (k=1,2,…,n-1) (7) 此时,建立数据时间序列的影子方程,则有: (8) 式中,d为方程的微分子,不可约分[15]。此时求解微分方程,则有: (9) 式中,T(1)v为原始数据累加后T(1)的映射值。此时,将式(9)代入,则T(1)的数据时间序列模型为: (10) 式中,e为无理数,此时,将(10)中累加的数据时间序列进行删除,则需要做一阶累减,形成原始数据序列的预测数据序列,则T(1)数据时间序列模型的还原值为: (11) (12) 为检测此次设计的时间序列数据深度挖掘模型,设计模型性能实验。此次实验数据选取某区域的电力局电力数据,采集该电力局近3年用户负荷功率数据和辅助输入数据作为此次的实验数据。短期电力负荷预测网络迁移变化如图4所示。 图4 短期电力负荷预测网络迁移变化 从图4中可以看出,该电力局共有36条支线路连接该区域的电力负荷,且电力用户多集中在这片区域中。因此,此次短期电力负荷采集时间间隔为15 min,负荷数据变换的时间序列为96维度。由于此次设计的时间序列数据挖掘模型,主要用来预测短期电力负荷变化情况,因此在此次实验中,验证时间序列数据深度挖掘模型性能,采用0~1标准化消除数据存在的幅值大小差异,提高数据采集使用效果。此时,针对得到的电网数据信息,需要进行聚类分析,得到电特性子集,获得数据聚类结果,对输入数据的时间序列进行分割,从而得到最终输入的该电力局电力数据。 上述数据为用户负荷功率数据,除用户负荷功率数据外,还需要辅助输入数据。即收集用户负荷功率数据时的日期、天气、温度等辅助输入数据信息,并对这些辅助输入数据信息进行量化处理,量化标准见表1。 表1 辅助输入数据量化标准 基于表1,对收集的辅助输入数据进行量化处理。此时,即可将采集到的用户负荷功率数据和辅助输入数据合并,即为此次实验需要的电力数据。基于上述流程收集到的电力信息,将此次实验设计的时间序列数据深度挖掘模型,放置在R730机架式服务器上运行。服务器的处理器为E5-2630 V3,运行频率为2.4 GHz,内存为32 GB。 基于此次实验设置的实验参数,将此次研究的时间序列数据深度挖掘模型作为A模型,将引言里提到的2种时间序列数据深度挖掘模型作为B模型和C模型。基于此次设计的时间序列数据深度挖掘模型,主要用于短期电力负荷预测,采用3种模型分别预测该电力局的短期电力负荷情况,从预测短期电力负荷功率和模型预测短期电力负荷的精确度2方面,分析3种时间序列数据深度挖掘模型,检测3种时间序列数据深度挖掘模型,预测短期电力负荷功率,与实际短期电力负荷功率是否一致;统计短期电力负荷功率预测结果,对比3组模型对短期电力负荷预测的精确度。为了保证此次实验模型对短期电力负荷预测的可靠性和真实性进行50次实验,并将所得短期电力负荷功率和模型预测短期电力负荷的精确度对比结果,按实验次序绘成图表,比较不同时间序列数据深度挖掘模型存在的差异。 基于上述设置的实验参数,分别采用3组模型对此次采集到的电力数据,进行短期电力负荷预测,并将预测结果与短期电力实际负荷进行对比。实验结果如图5所示。 图5 短期电力负荷对比结果 从图5中可以看出,经过50次预测结果,B模型对短期电力负荷预测与实际短期电力负荷值走势不一致,呈现平稳趋势,相较实际值,所预测的短期电力负荷功率值较低,未出现明显峰值;C模型对短期电力负荷预测,出现峰值较多,而在实际值中,仅在预测的第28次和36次存在峰值;而A模型与实际值的走势、峰值等较为接近,得到的负荷功率值也极为接近。由此可见,此次研究的时间序列数据深度挖掘模型,可以准确预测短期电力负荷。 预测效果如图6所示。 图6 预测效果 由图6可知,拟合电力负荷曲线上表现优异,预测数据在接近分割线部分预测较为准确,远离分割虚线处开始出现衰退。这是因为此处的输入预测数据为前一时间点的预测数据,通过计算得出下一时间点的预测数据,预测的误差开始叠加,导致精度下降,而接近分割线的部分由于是真实数据预测出的预测数据,故而较为准确。 在第1组实验的基础上,进行第2组实验。基于此次实验采集的电力数据,所采集到的181个样本数据,验证模型预测短期电力负荷精确度,收集第1组实验预测过程中,模型产生的规则数目变化、准确预测样本数、样本搜索的准确率、负荷的平均预测准确率等5个方面,对比模型在预测短期电力负荷过程中3组模型的精确度。 多变量的预测方式为每一日的同一时刻作为一个时间序列数据,同时预测 24 个时间序列的负荷值,多变量预测结果如图7所示。 图7 多变量数据预测效果 由图7可以看出,多变量预测时存在个别时间点预测误差较大,整体预测负荷与真实负荷拟合程度较好。其模型预测短期电力负荷精确度对比结果见表2。 表2 模型预测短期电力负荷精确度对比 从表2中可以看出,在验证同样的样本数目下,A模型对此次采集到的样本数据准确预测的样本高于B模型和C模型,对模型中的规则使用更是远远高于B模型和C模型,样本搜索准确率也高达90%以上,对短期电力负荷预测准确率更是达到了98%。由此可见,此次研究的时间序列数据深度挖掘模型对短期电力负荷预测精确度更高,对模型自身的规则设定的准确率更高。 综合上述2组实验可知,此次研究的时间序列数据深度挖掘模型,可以准确预测短期电力负荷功率,对模型设定的规则使用率高。 综上所述,通过此次研究的时间序列数据深度挖掘模型,可以得到数据时间序列的变化情况,从而预测短期电力负荷。但是,此次研究的时间序列数据深度挖掘模型未曾考虑负荷电价的敏感程度,对模型预测电力负荷产生的影响。因此,在今后的研究中,需要深入研究负荷电价变化,进一步提高电力负荷预测的准确率。


1.3 预测短期电力负荷

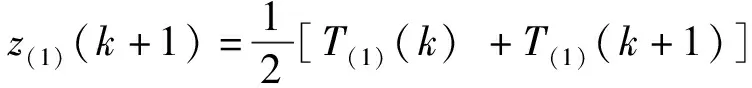

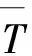
2 实验研究


2.1 第1组实验测试结果

2.2 第2组实验测试结果


3 结语

