基于机器学习的油菜籽含油量预测

周 圣

（武汉轻工大学 湖北武汉 430000）

我国是油料生产和消费的大国，主要的油料作物有油菜、大豆、向日葵、胡麻、芝麻等[1]。油料及其相关制品都具有非常丰富的营养功能成分，如蛋白质、脂肪酸、维生素等，为人类的正常活动提供了必需的能量和营养物质[2]。气相色谱法、液相色谱法、索氏提取法或联用技术是目前油料品质检测通常采用的方法。传统化学方法如字面一般，无一例外都需要使用化学试剂，操作较为烦琐，耗时较长，成本普遍偏高，且无法满足现场快速无损检测的需要。相较于这些传统化学方法，近红外光谱技术是一种绿色、无损的快速检测技术，具有操作简单、检测成本低、无须化学试剂、绿色环保，以及可实现多品质参数同步检测等优点，广泛应用于油料品质的无损快速检测。

近红外光谱区的波长范围介于中红外光谱区和可见光区域之间。近红外光谱主要是含氢基团伸缩和弯曲振动的倍频与合频吸收，通过透射和漫反射两种方式获得，主要用于分析固、液、气三态样品的物理化学性质[2]。

化学计量学方法同近红外光谱技术紧密结合，已广泛应用于油料产品品质的速测。近红外光谱技术在快速测定油料特异品质中发挥着更重要的作用，然而该技术无法像气相色谱等传统化学方法那样得到更加精确的数值，本文提出了一种基于LinearSVR（线性支持向量回归）的模型，用以快速预测油菜含油量，并取得了较好的结果。

1 预测模型

1.1 支持向量SVM

支持向量机（SVM）是机器学习中较为常见的一种分类算法，支持向量机作为二分类模型，寻找一个超平面（假若数据集是X维的，那么就需要X-1维的某个对象来对数据进行分割，这个分类的决策边界就被称为超平面）是它的最终目标。分割样本遵循的规则是使间隔最大化，最终问题的实质是对一个凸二次规划问题进行求解。在二维空间中的点仅能使用非线性的超平面才能分割开来，而映射到高维空间中，就能够使用一个线性的平面给分割开。支持向量机需要完成的任务就是在这些能够选择的直线中选择一条最优的直线作为分类的直线。遇到的情况分为几种：（1）对于线性可分的训练样本，学习一个线性可分支持向量机，采用硬间隔最大化的方法；（2）对于近似线性可分的训练样本，学习一个线性支持向量机，使用方法是软间隔最大化；（3）对于线性不可分的训练样本，学习一个非线性支持向量机，方法为软间隔最大化和核技巧。在它们当中，坐落在数据边界的两边超平面上的点称为支持向量，即对于点的“犯错”的忍耐度越大越好，通俗来讲就是函数的间隔越大越好，最终拟合线也是由这些点来确定的。

1.2 线性支持向量回归LinearSVR

超平面表达式：f(x) =wTx+b。其中f(x)表示目标超平面，b表示偏置参数，wT表示权重参数。在SVR中，认为只要f(x)与y偏离不大，即算预测正确，ε为拟合精度控制参数。

支持向量回归表示，凡是在虚线内部的值均可认为是预测正确，需要计算的只有虚线外部值的损失。在日常的实际任务中很难确定一个切合的核函数来使得训练样本在特征空间中线性可分，适逢找到了某一个核函数使得训练集在特征空间中线性可分，但也不能够肯定是不是由于过拟合所造成的这个似乎是线性可分的结果。容许支持向量机在某些样本上出现错误是解决这个问题的一个好办法，因此就需要软间隔（soft margin），即在前面介绍的支持向量机是要求在所有样本均满足超平面表达式的约束条件下，允许部分样本不满足约束，考虑到SVM中线性不可分的情形，引入拉格朗日乘数，得到线性拟合函数为：

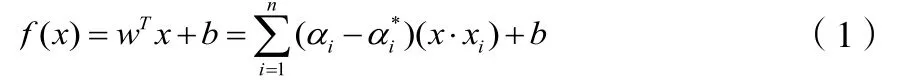
这之中αi、αi*表示拉格朗日乘子。在线性不可分的情况下，支持向量机首先是在低维空间之中完成计算，再将输入空间映射到高维特征空间，使用的方法是核函数，最后是构造，在高维特征空间中构造出最优分离超平面，从而把平面上那些本身并不好分的非线性数据分开。利用低维的输入空间，使其转换为高维空间，即将不可分离的问题转化为可分离问题，这些函数称为核。引入核函数，则得：

2 实验分析

文中使用的数据来自中国农业科学院油料作物研究所。由于影响油菜含油量的因素众多，在考虑各种的因素相关性之后，探究了油菜种子中脂肪酸组分同含油量的相关性，得到图1。

图1 相关系数热力图

关于误差的评价指标常用的有MAE、MSE、RMSE、statD、MAPE、VAF等。本文研究的内容是含油量的预测问题，指标之间是大同小异的，所以应当选取其中最为合适的指标来评价预测的误差。因此，本文仅选取MSE具有代表性的指标来评价模型的预测效果。

其中，yi为产品销量的预测值，为产品销量的实际值。MSE被称为均方误差，从表达式中也能够看出，MSE值越小，模型的预测效果越好。

选取C16-0、C18-0、C18-1、C18-2、C18-3、C20-1、C22-1、C22-1IN、C22-1LOW，共九项指标作为模型的输入，以油菜含油量这一项作为模型的预测输出。以LinearSVR预测模型进行分析，该模型的平均相对误差为1.725。表1为随机选取200 份材料中的10 份样本进行模型预测值与实际值的差值比较的结果。

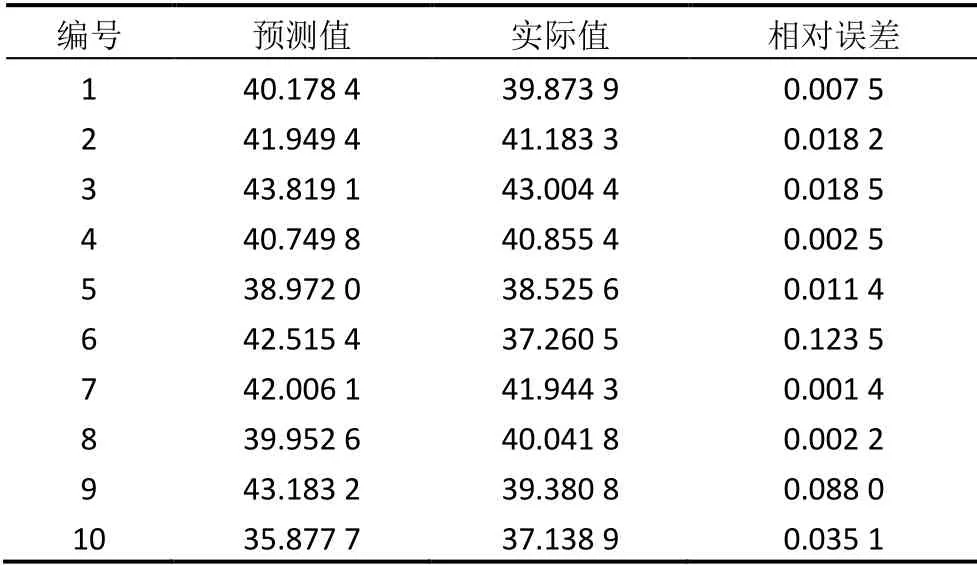
表1 模型预测值同实际值的差值比较

由表1可知，预测模型具有良好的预测精度。

图2是预测模型对随机选取的10 份样本的预测曲线图，图中的两条曲线是分别根据产品的预测含油量和实际含油量数据绘制而成，将其放置在一张图中能够更加直观地观察预测误差变化的情况。

图2 油菜含油量预测

3 结论

本文提出了基于LinearSVR的油菜含油量预测模型，SVR通过核函数将训练样本数据进行非线性映射至高维特征空间，并在此高维空间进行回归预测。实验表明，本文提出的基于LinearSVR的油菜含油量预测模型具有良好的预测准确度。与此同时，后续的改进及创新主要为：油菜含油量受多种因素影响，相互间的关系也较为复杂，接下来的工作中，可能考虑引入多目标的混合算法，通过对受多个因素影响的含油量进行最优规划，进而得到更加准确的模型预测值。