Exponential Growth of Solutions for Nonlinear Coupled Viscoelastic Wave Equations with Degenerate Nonlocal Damping and Source Terms

(Department of Mathematics,Henan University of Technology,Zhengzhou 450001,China)

Abstract:This paper is concerned with a system of nonlinear viscoelastic wave equations with degenerate nonlocal damping and memory terms.We will prove that the energy associated to the system is unbounded.In fact,it will be proved that the energy will grow up as an exponential function as time goes to infinity,provided that the initial data are positive initial energy.

Keywords:Exponential growth;Nonlocal damping;Positive initial energy;Viscoelastic wave equations

§1.Introduction

In this work,we consider a system of viscoelastic wave equations with degenerate nonlocal nonlinear damping and nonlinear source terms

wherek,l≥0,m,r≥1,Ωis a bounded domain inRn(n≥1)with a smooth boundary∂Ω,giandfi(i=1,2)are nonlinear functions,and||u||represents the norm ofuonL2(Ω),i.e.||u||2=dx.

The single wave equation of the form

is derived from the nonlocal plate equation proposed by Lange and Perla Menzala[11].Later,Equation(1.2)was studied by Cavalcanti et al[4]in a viscoelastic formulation,by adding a memory term-(g*Δu)(t).Equation(1.2)models the vibrations of viscoelastic beams and plates(whenn=1,2).The nonlocal nonlinearityis indeed a damping term.It models a frictional mechanism acting on the body that depends on the average ofuitself,which arises in the theory of viscoelasticity,physics and material science.Such type problems are interesting to study from the point view of mathematics.There is a large literature concerned with the plate or beam equation.More recently,Narciso[16]concerned with the well-posedness as well as the asymptotic behavior of solutions for the following model

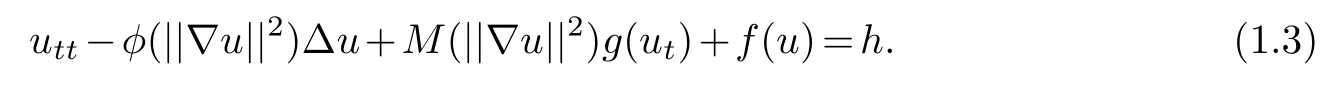
They proved that the energy associated with(1.3)is exponential stability whenh=0 by Nakao’s inequality.Li et al[12]proved a general energy decay property for solutions of(1.3)with frictional boundary damping.Zhang et al[25]consider a wave equation with nonlocal nonlinear damping and source terms.They prove a general energy decay property for solutions by constructing a stable set and using the multiplier technique.

WhenMin(1.3)is nondegenrate,that is,there existsm0＞0 such thatM(s)≥m0for alls≥0,then a full damping is in place and the exponential decay follows trivially[5].For the related study on this topic,one can see[4,13,15,16,20,21]and references therein.For the degenerate case(that is,M(s)≥0 for alls≥0),to our best knowledge,the only paper is given by Cavalcanti et al[5].They established a well-posedness result and an exponential decay result for solutions of equation(1.3)whenφ(||∇u||2)=1,M(||∇u||2)=||∇u||2andg(ut)=ut.More comments on the decay rates of energy in degenerate damping case can be found in[5].As pointed in[5],for the degenerate case,the exponential decay problem is a more challenging problem since the traditional multipliers do not work for this kind of wave equation with nonlocal damping term given by||∇u||2lut.Definitely the attempt at achieving the uniform stability for wave models with nonlocal damping such as||∇u||2lutturns out to be a very hard task.A natural question which arises is how does the energy behave whentgoes to infinity?

To the best of our knowledge,the systems of viscoelastic wave equations with degenerate nonlocal damping terms have not been well studied.In this paper,we investigate problem(1.1),in which the polynomial degenerate damping(i.e.M(||∇u||2)g(ut)=||∇u||2l|ut|ρut)and the presence of viscoelastic term will be considered.We prove the exponential growth of solutions for problem(1.1)with positive initial energy.We also prove the exponential growth of solutions for problem(1.1)when the initial energyE(0)of our solutions is negative,which means that our initial data are large enough.The key ingredient in our proof is a method used in Vitillaro[22]and developed in[18]for the following system of wave equations

with necessary modification imposed by the nature of our problem.The same idea has been used in[6,7,9,14,17,19,24].As a special case,fork=l=0,problem(1.1)becomes the system(1.4).The main difficult in this paper is to handle with the term(andthat arises from the degenerate damping term||∇u||2k|ut|m-2ut(and||∇v||2l|vt|r-2vt).

It is also worth mentioning that there is a wide literature which addresses hyperbolic models with nonlinear degenerate displacement-dependent damping terms similar toσ(u)g(ut),whereσ(u)is a positive function andgis nonlinear.Here,we cite[1–3,8,10]as examples.For more related works on this topic,one can see[5]for more details.We mention also that some special cases of the single wave equations with nonlinear damping and nonlinear source terms in the form

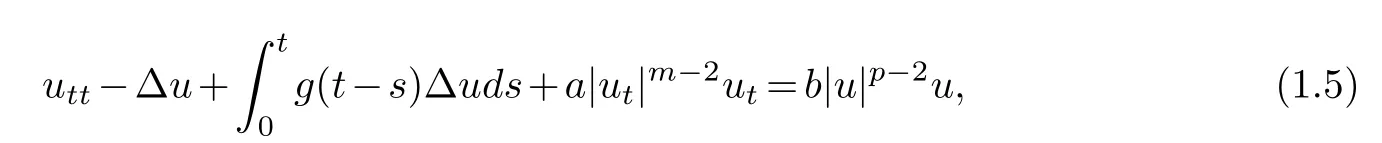
has been extensively studied and results concerning existence,blow up and asymptotic behavior of smooth,as well as weak solutions have been established by several authors over the past decades(see[23]for details).

Our plan in this paper is as follows.In Section 2,we present some lemmas and notations need later of this paper.In Section 3,we establish the energy will grow up as an exponential function as time goes to infinity,provided that the initial data are large enough.

§2.Preliminaries

Throughout this paper,for 1≤p＜∞,||.||pdenotes theLp(Ω)norm and we write||.||2by||.||for simplicity.The inner product inL2(Ω)is denoted by(.,.).We also consider the spacewith norm||∇.||.The constantsCi,i=0,1,2,...used throughout this paper are positive generic constants,which may be different in various occurrences.

In this paper,we consider the problem(1.1)with

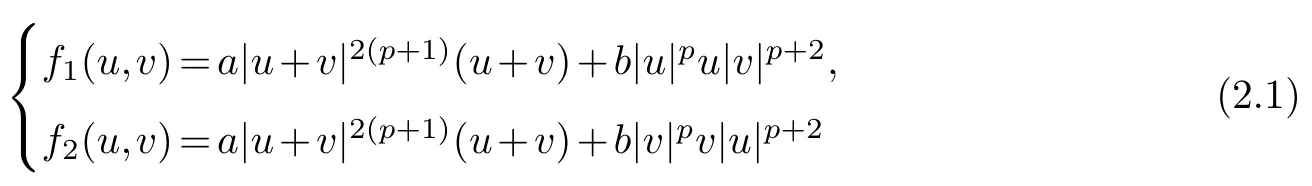
as source terms,in which the constantsa＞0,b＞0.We suppose thatpandmsatisfy

It is clear that from(2.1),we obtain

where

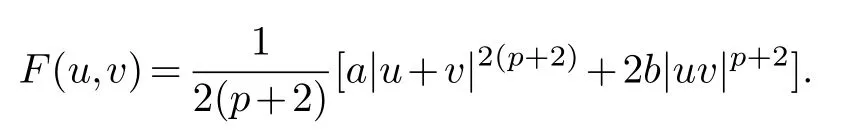
There are two positive constantsc0,c1such that

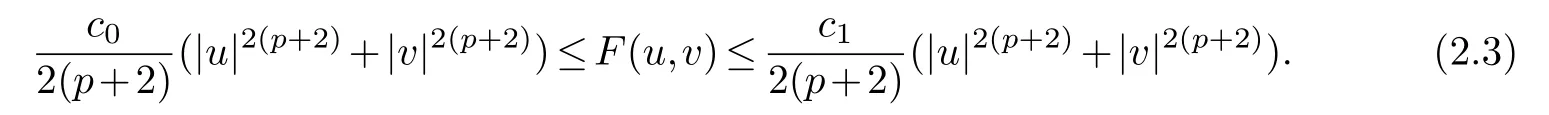
Now,we make the following assumptions on theC1-nonnegative and nonincreasing relaxation functionsg1andg2:

Furthermore,letρbe any fixed number such that 2＜ρ＜2(p+2),we assume that

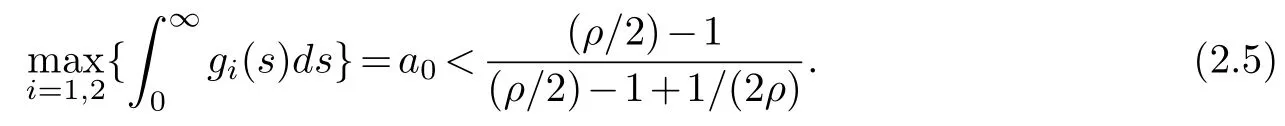
We introduce the energy functionalE(t)associated to our system

where

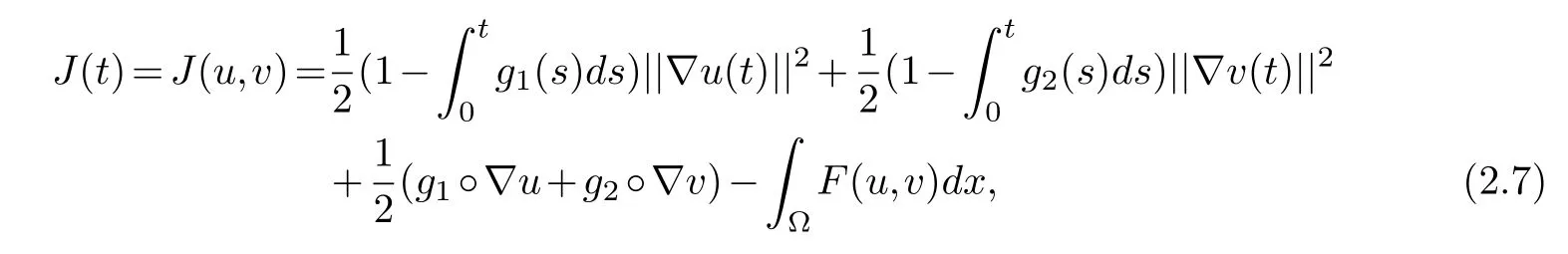
and

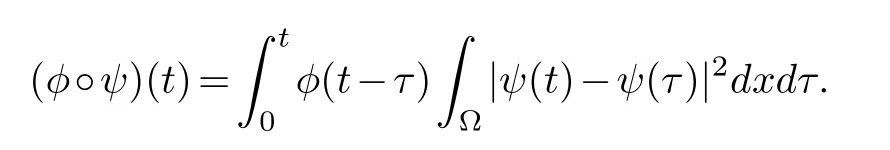
Let us define

Moreover,for any solution of problem(1.1)the energy functional satisfies

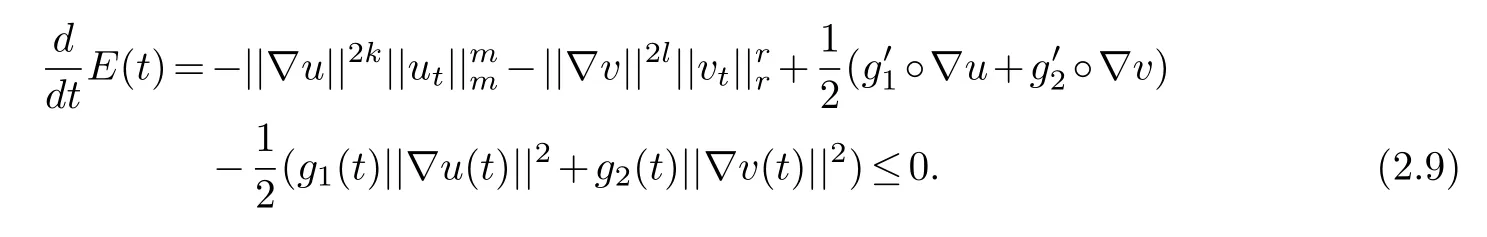
Now,we recall the following local existence theorem,which can be established by using the argument in[6,7,15,21].

Theorem 2.1.Assume that assumptions(2.2),(2.4)and(2.5)hold,if u0,v0∈H2(Ω)∩(Ω),u1,v1∈L2(Ω),then problem(1.1)possess a weak solution u in the class

where W2=H2(Ω)∩(Ω).In addition,it is possible to find that

In the next theorem we give the global existence result,its proof is based on the concept of socalled stable set.In our problem,the stable setWcan be defined as followsW={(u,v)∈(Ω)×(Ω),J(u,v)＜d,I(u,v)＞0},whered=inf{supλ≥0J(λu,λv),(u,v)∈(Ω)×(Ω)(0,0)}＞0,which is called the well depth.As mentioned in the introduction,the main difficult in this paper is to handle with the term||∇u||2k|ut|m-2ut(and||∇v||2l|vt|r-2vt),which is similar to that of[15,21]and so the approaches employed in[15,21]can be applied here with some modifications.However,the term||∇u||2k|ut|m-2ut(and||∇v||2l|vt|r-2vt)can not effect the stable set.In the following theorem,we show that if we restrict our initial data in the stable set,then our local solution obtained is global in time.It can be got by using of arguments in[23].Here,we don’t give the details.

Theorem 2.2.Suppose that(2.2),(2.4)and(2.5)hold,and(u,v)is a local solution of problem(1.1)-(1.3)on[0,T).If(u0,v0)∈W,u1,v1∈L2(Ω)and E(0)＜d,then(u,v)is a global solution of the problem(1.1).

§3.Exponential growth of the solutions

In this section,we will prove that the energy will grow up as an exponential function as time goes to infinity,provided that the initial data are large enough.Our techniques of proof follow very carefully the techniques used in[6,7,17–19,24].

We shall need the following lemma.

Lemma 3.1.[19]Suppose that(2.2)holds.There existsη＞0,such that for any(u,v)∈(Ω)×(Ω),the inequality

holds.

In order to prove our result and for the sake of simplicity,we takea=b=1 and introduce the following:

whereηis the optimal constant in Lemma 3.1.The following lemma will play an essential role in the proof of our main result,and it is similar to a lemma used first by Vitillaro[22].

Lemma 3.2.[19]Assume that(2.2)and(2.5)hold.Let(u,v)be the solution of problem(1.1).Assume further that E(0)＜E1and＞α1.Then there existsa constantα2＞α1such that

Here,we denote

Theorem 3.1.Let2(p+2)＞,0≤k,l＜1,u0,v0∈(Ω),and u1,v1∈L2(Ω).Then the solution to problem(1.1)grows as an exponential function in L2(p+2)(Ω)-norm providedthe initial data satisfying the condition of Lemma 3.2.

Proof.We define

By(2.9),we have

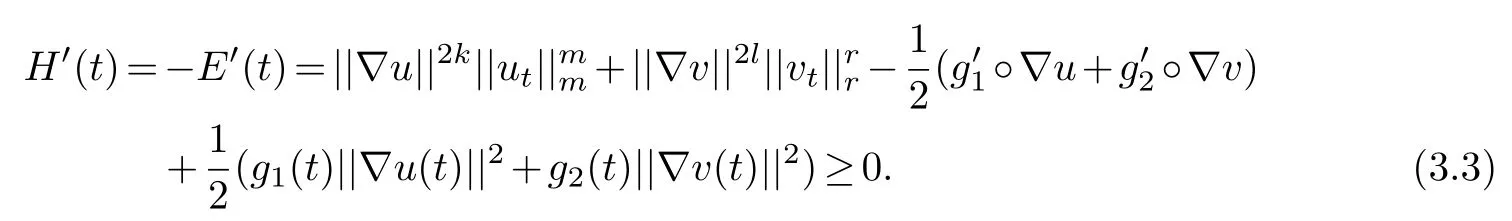
Consequently,from(2.4),(2.6),(2.3)and Lemma 3.2,we have

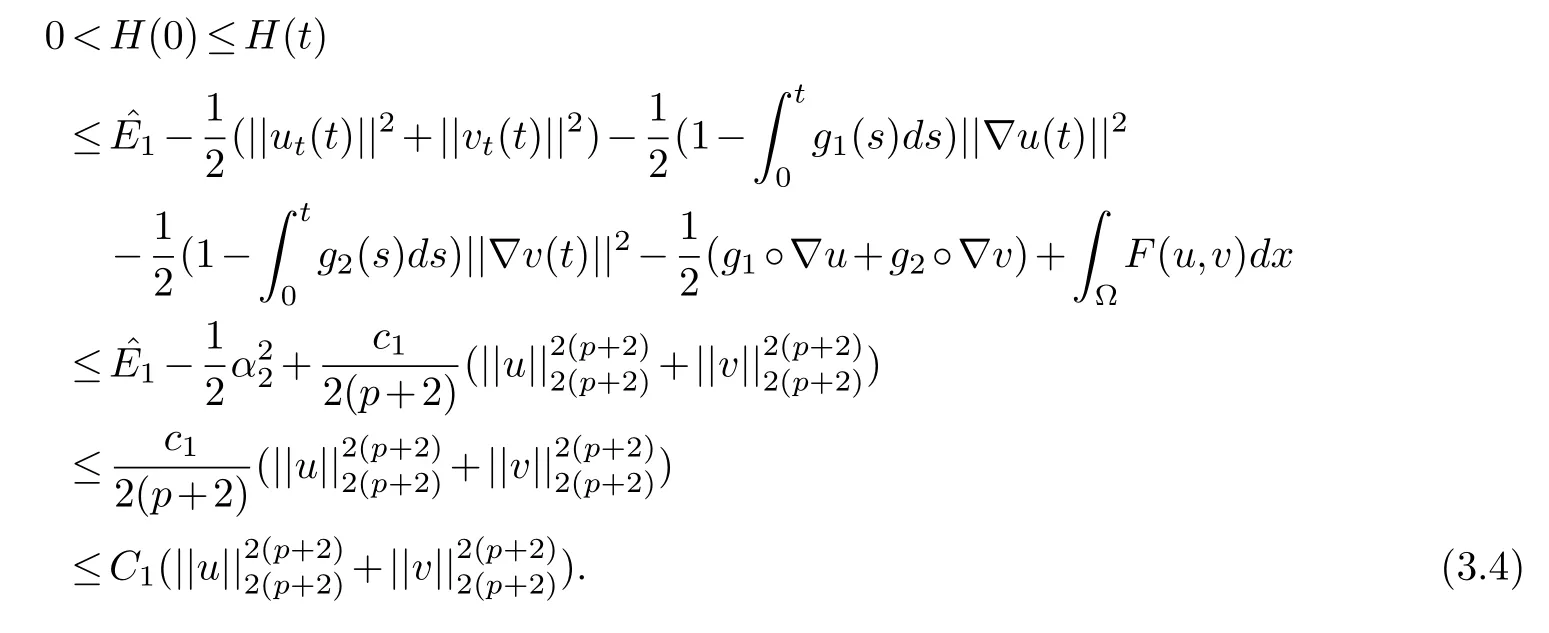
Now,we introduce the main auxiliary function

where∈is a small positive constant to be fixed later.

By differentiating with respect tot,using(3.5)and problem(1.1),we have

where,for simplicity,we denote

By the definition ofE(t)and(3.2),we obtain

Using Cauchy-Schwarz and Young’s inequalities,we get

for anyλ＞0.Similarly,we obtain

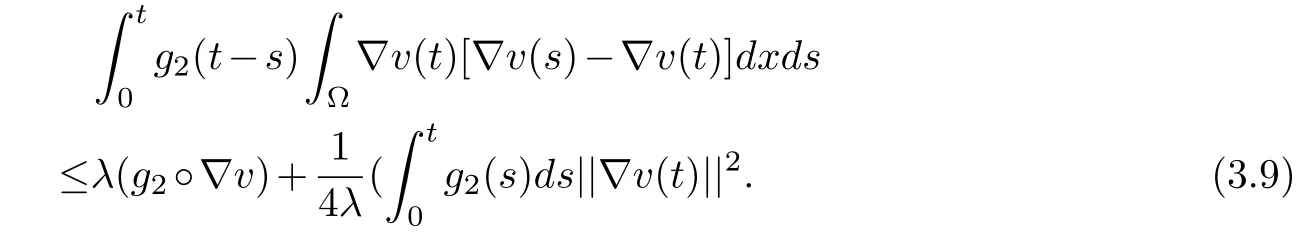
Taking into account(2.5),substituting(3.7),(3.8),(3.9)and(2.3)into(3.6),we get

for some 0＜λ＜ρ/2.For the termG(t)in(3.10),by applying Holder’s inequality,Young’s inequality,and(3.3),we obtain

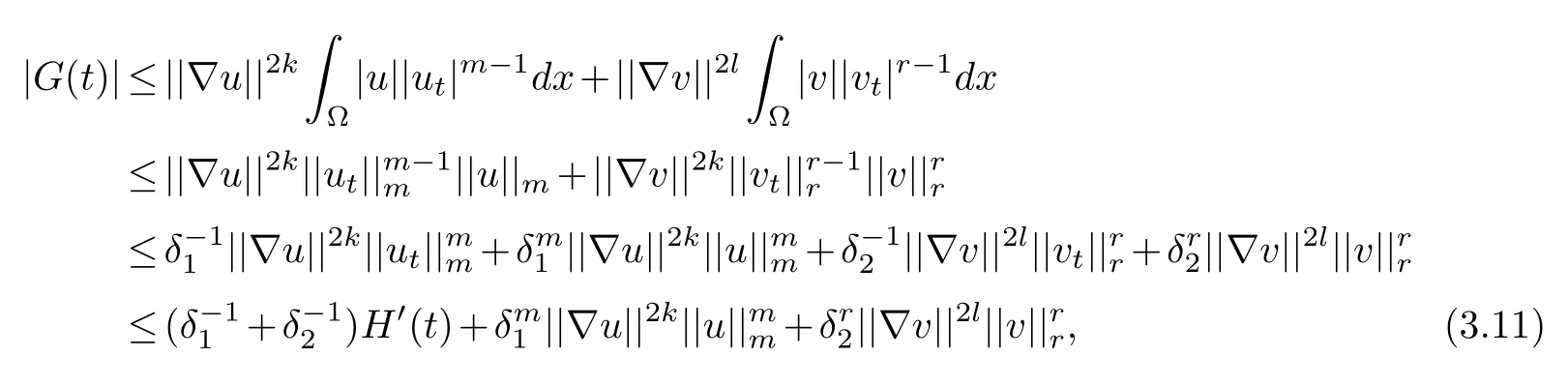
for anyδ1,δ2＞0.

By using(3.11),then(3.10)becomes

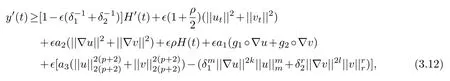
whereHere,we have used the fact that

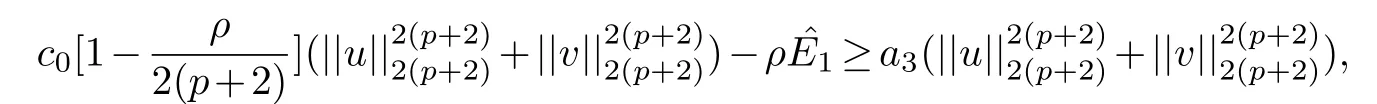
which can seen from Lemma 3.2,and one can easily check thata3＞0,sinceα2＞α1and the definition ofE1andα1.

Now,we estimate the last two terms in(3.12).Since 2(p+2)＞max{m,r},we have

Then,by using embedding theorem,Lemma 3.2,2(p+2)＞max,(3.4)and(3.13),we get

We can chooseδ1,δ2＞0 such that

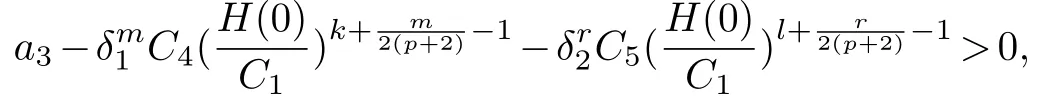
then,we arrive at

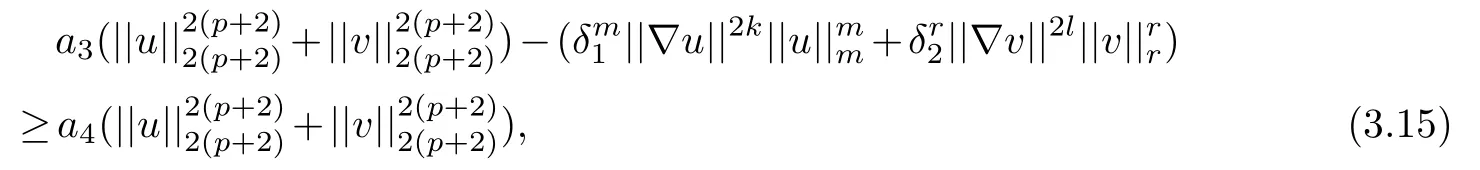
wherea4=.Onceδ1,δ2＞0 are fixed,we pick∈small enough so that＞0 andy(0)≥0.Then,taking account into(3.15)and(3.3),we can find positive constantsC6such that(3.12)becomes

Then,we have

Sincep＞2,using the algebraic inequality

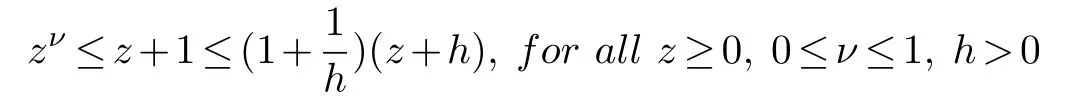
and(3.4),we get

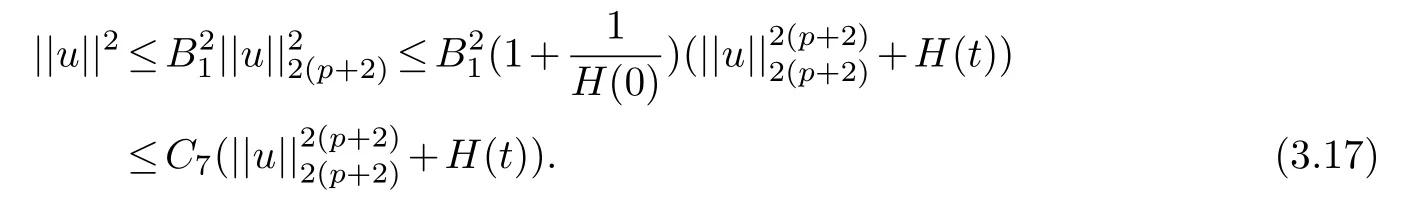
On the other hand,sincep＞2,Holder inequality and(3.17)implies

Similarly,we have

Hence,from(3.18),(3.19)and the definition ofy(t),we arrive at

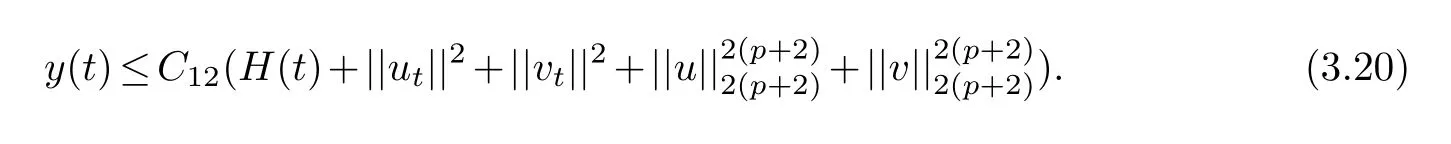
Thus,(3.16)and(3.20)show that

Integrating the differential inequality(3.21)between 0 andtgives following estimate fory(t)

On the other hand,from the definition of the functiony(t)(and for small values of the parameter∈),it follows that.

From the two inequalities(3.21)and(3.22),we conclude the exponential growth of the solution(u(t),v(t))to problem(1.1)inL2(p+2)(Ω)norm,which implies the conclusion desired.