Entropy and Similarity Measure for T2SVNSs and Its Application
(1.Foundation Department,Sichuan Institute of Industrial Technology,Deyang 618500,China;2.School of Science,Southwest Petroleum University,Chengdu 610500,China)
Abstract:The objective of this paper is to present a new approach for solving the multi-
Keywords:Type-2 single valued neutrosophic set;Entropy;Tangent function;Similarity measure;MCGDM
§1.Introduction
Neutrosophic set[32]is an important tool for dealing with problems involving uncertainty,indeterminacy and inconsistency.Wang et al.[33]developed the concept of SVNSs,which is a subclass of the neutrosophic sets(NSs)for solving scientific and engineering problems.SVNSs have been widely used in different fields,like engineering problems,[12,34]medical problems,[1,2,11]image processing problems,[10,17,18]decision-making problems,[25,29,37]social problems[22,26],conflict problems[27].Many scholars have also studied type-2 fuzzy sets,such as Yang et al.[35]introduced the similarity of type-2 fuzzy sets,they also investigated its properties,Hung et al.[13]proposed similarity methods between two type-2 fuzzy sets,at this moment,the properties of these methods were obtained.Sing[31]introduced two type-2 fuzzy sets based on the distances between Euclidean and Hamming.Zhao et al.[39]have studied type-2 intuitionistic fuzzy set(T2IFS),they gave the concept of T2IFS,and discussed the relation of T2IFS.Cuong et al.[8]introduced some operations between two T2IFSs.
Similarity measure is becoming important in decision making problems.Some strategies[7,14]are proposed to measure the similarity between fuzzy sets,whereas these strategies can not deal with the similarity measures involving uncertainty and inconsistency.In the references,some scholars have discussed the similarity measures of NSs.[3,4]Mondal et al.[23,36]proposed sine hyperbolic similarity measure and tangent similarity measure methods to deal with MADM problems.Lu et al.[24]proposed logarithmic similarity measure and applied it in fault diagnosis strategy under interval valued fuzzy set environment[19].In addition to similarity measurement,there are other aspects of research,such as:correlation coefficient[30],TOPSIS method[5],aggregating operators[9,15,21].
Based on the above analysis,few scholars have studied the MCGDM method using tangent similarity measure,so the main contents of this paper are:
(1)To define a new similarity measure under T2SVNS environment and prove its basic properties.
(2)To define a new entropy function of T2SVNSs to determine the weight of unknown attributes.
(3)To develop a MCGDM model based on proposed entropy and similarity measures.
(4)To present an illustrative example and comparative analysis to illustrate effectiveness and feasibility of the proposed method.
The rest of this paper is structured as follows.In section 2,the concepts of SVNSs and T2SVNSs are given.In section 3,we define tangent similarity measure between two T2SVNSs and prove its properties.In section 4,a new entropy funtion to compute unknown attribute weights for T2SVNSs is proposed.In section 5,we propose a MCGDM method based on entropy and tangent similarity measures of T2SVNSs.In section 6,an example and comparative analysis are given to illustrate effectiveness and feasibility of the proposed method.In section 7,we come to the conclusion.
§2.Preliminaries
2.1.Single valued neutrosophic sets(SVNS)
Definition 2.1.[38]Let X be a universal space of points(objects),with a generic element in X denoted by x,single valued neutrosophic set(SVNS)Q⊂X is characterized by truth-membership function tq(x),indeterminacy-membership function iq(x)and falsity-membership function fq(x).
A SVNS can be expressed as

where tq(x),iq(x),fq(x)are real standard or nonstandard subsets of[0,1],so that it means tq(x):X→[0,1],iq(x):X→[0,1],fq(x):X→[0,1],with the condition of0≤suptq(x)+supiq(x)+supfq(x)≤3,for all x∈X.
When X is continuous,a SVNS Q can be written as

When X is discrete,a SVNS Q can be written as

Definition 2.2.[33]Let P and Q be two SVNSs,
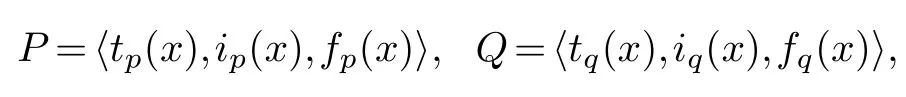
then,for all x∈X,operations can be defined as follows:
(x)≥tp(x),iq(x)≤ip(x),fq(x)≤fp(x).
(2)P=Q,iff,P⊆Q and Q⊆P.
(3)The complement of a SVNS P is denoted as P c,which is defined astpc(x)=fp(x),ipc(x)=1-ip(x),fpc(x)=tp(x).
(4)QP=〈max(tp(x),tq(x)),min(ip(x),iq(x)),min(fp(x),fq(x))〉.
(5)QP=〈min(tp(x),tq(x)),max(ip(x),iq(x)),max(fp(x),fq(x))〉.
Definition 2.3.[20]Let Q and P be two SVNSs,t

hen,∀k∈R,there is
(1)Q⊕P=〈tq(x)+tp(x)-tq(x)·tp(x),iq(x)·ip(x),fq(x)·fp(x)〉.
(2)Q⊗P=〈tq(x)·tp(x),iq(x)+ip(x)-iq(x)·ip(x),fq(x)+fp(x)-fq(x)·fp(x)〉.
(3)λQ=(1-(1-tq(x))k,iq(x)k,fq(x)k).
(4)Qk=(tq(x)k,1-(1-iq(x))k,1-(1-fq(x))k).
2.2.Type-2 single valued neutrosophic set(T2SVNS)
Definition 2.4.[16]A T2SVNS~N is a set of pairs{μN(a),ηN(a),νN(a)},a∈A,μN(a),ηN(a)andνN(a)are respectively called true membership,uncertain membership and false membership,which are defined as follows:

where uN,nN and vN are named Primary truth-membership function(Ptmf),Primary indeterminacy membership function(Pimf)and Primary falsity-membership function(Pfmf).ta(uN),ia(nN)and fa(vN)are called Secondary truth membership function(Stmf),Secondaryindeterminacy membership function(Simf)and Secondary falsity-membership function(Sfmf).,andare called as primary truth membership,primary indeterminant membership andprimary falsity membership,respectively.

For convenience,can be abbreviated as=〈(uN,ta(uN),nN,ia(nN),vN,fa(vN))〉,which is called type-2 single valued neutrosophic number(T2SVNN).From now on,the set of all T2SVNS over the universe A will be denoted bySV2(A).
Definition 2.5.1=〈(uN1,ta(uN1),nN1,ia(nN1),vN1,fa(vN1))〉and2=〈(uN2,ta(uN2),nN2,ia(nN2),vN2,fa(vN2))〉be two T2SVNSs,∀a∈A.Then,
(1)if and only if uN1≤uN2,ta(uN1)≤ta(uN2),nN1≥nN2,ia(nN1)≥ia(nN2),vN1≥vN2,fa(vN1)≥fa(vN2).
12if and only ifand.
(3)=〈vN1,fa(vN1),1-nN1,1-ia(nN1),uN1,ta(uN1)〉.
(4)=〈max(uN1,uN2),max(ta(uN1),ta(uN2)),min(nN1,nN2),min(ia(nN1),ia(nN2)),min(vN1,vN2),min(fa(vN1),fa(vN2))〉.
(5)=〈min(uN1,uN2),min(ta(uN1),ta(uN2)),max(nN1,nN2),max(ia(nN1),ia(nN2)),max(vN1,vN2),max(fa(vN1),fa(vN2))〉.
§3.Tangent similarity measures for T2SVNSs
Definition 3.1.Assume that12∈SV2(A),similarity measure based on tangent functionbetween two T2SVNSs is defined as follows:
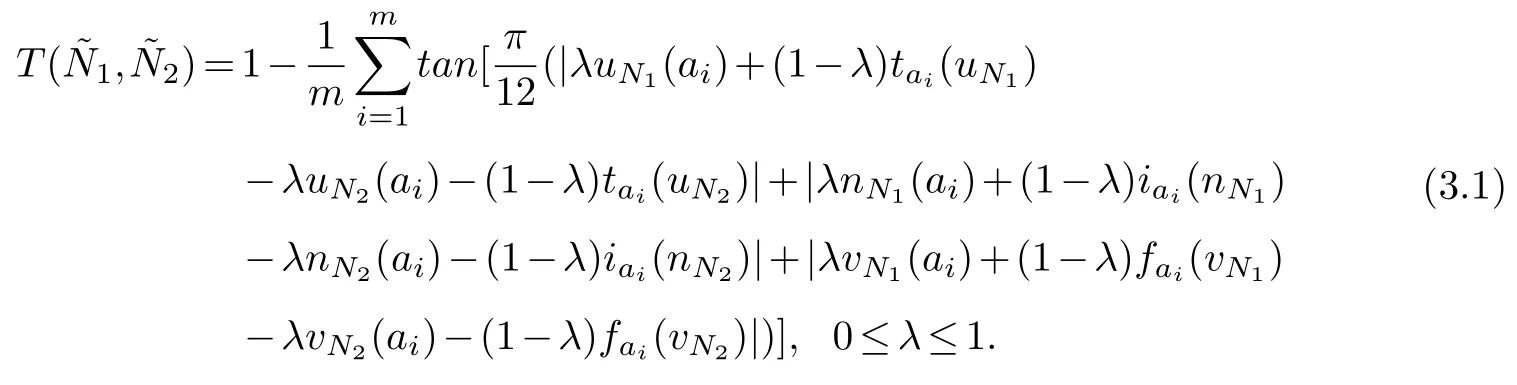
Theorem 3.1.The defined tangent similarity measure T(12)of two T2SVNSs,the basicoperations are satisfied as follows:
(1)1≥T(12)≥0.
(2)T(12)=1 if and only if1=2.
(4)if3∈SV2(A)123,then T(13)≤T(12)and T(13)≤T(23).
Proof.(1)Tangent function increases monotonically on the interval[0,].It also depends on the interval[0,1].Therefore,0≤T(12)≤1.
(2)Assume that two T2SVNS,0≤λ≤1,



soT(13)≤T(12).In the same way,

soT(13)≤T(23).
Definition 3.2.Assume that12∈SV2(A),weighted similarity measure based on tangentfunction between two T2SVNSs is defined as follows:
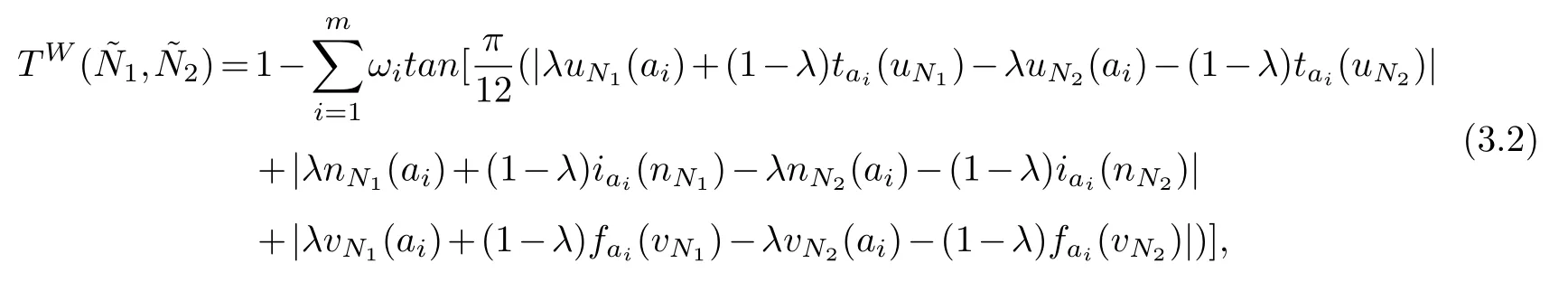
here,0≤λ≤=1.
Theorem 3.2.The defined tangent similarity measure T(1,2)of two T2SVNS,the basic operations are satisfied as follows::
He remembered such days from his own childhood in the mountains, rare moments of escape when he went into the woods, his breathing amplified74 and his voice somehow muffled75 by the heavy snow that bent branches low, drifted over paths
(1)1≥TW(1,2)≥0,
(2)TW(1,2)=1 if and only if1=2,
(3)TW(1,2)=TW(2,1),
(4)if3∈SV2(A)and1⊆2⊆3,then TW(1,3)≤TW(1,2)and TW(1,3)≤TW(2,3).
Proof.(1)Tangent function increases monotonically on the interval[0,].It also depends on the interval[0,1]and=1.So,0≤TW(1,2)≤1.

Therefore,TW(1,2)=1 for 0≤λ≤1 and=1.Conversely,

(3)Lets prove the third question



§4.A new entropy measure for T2SVNSs
Definition 4.1.The entropy function of a T2SVNS

is defined as follows:

Theorem 4.1.The entropy function Ej(N)satisfies the following properties:
(1)Ej(N)=0.if uNj(ai)+tai(uNj)=1,vNj(ai)+fai(vNj)=0,
(2)Ej(N)=1.if N=(0.5,0.5,0.5,0.5,0.5,0.5),
(3)Ej(N)≥Ej(N′).if

(4)Ej(N)=Ej(Nc).
Proof.(1)uNj(ai)+tai(uNj)=1,vNj(ai)+fai(vNj)=0⇒Ej(N)==0.
(2)N=(0.5,0.5,0.5,0.5,0.5,0.5)⇒Ej(N)==1-0=1.
(3)Lets prove the third question

(4)Since〈uN,ta(uN),nN,ia(nN),vN,fa(vN)〉c=〈vN,fa(vN),1-nN,1-ia(nN),uN,ta(uN)〉,we haveEj(N)=Ej(Nc).
§5.MCGDM method based on the entropy and tangent similarity measures of T2SVNSs
In this section,a MCGDM approach is presented by tangent similarity measures for T2SVNSs.Assume thatP={p1,p2,...,pd}be a committee of decision makers,A={A1,A2,...,Ak}be the alternatives,C={C1,C2,...,Cs}be the attributes of each alternative.Then,the following steps are described for finding the best alternative(s).
Step 1:Determination of the T2SVN decision matrix of the decision makers(DMs).
When an expert evaluate the given alternativesAiunder different attributesCjmade by decision makersPm(m=1,2,...,d)and represent their values in terms of T2SVNNs.Hence,decision matrixPm=can be written as follows:

where.
Step 2:Determination of the aggregating decision matrix.
The aggregating matrixB=(bij)k×sis expressed as follows:

Step 3:Determination of the ideal solution.
T2SVN local positive ideal solution(T2SVNPIS)and the T2SVN negative ideal solution(T2SVNNIS)are defined as follows:

Step 4:Determination the weights of attribute.
By Equation(4.2),we can calculate the attribute weights.
Step 5:Determination of separation measures from ideal solutions to each alternatives.
Separation measuresandof each alternative from ideal solutions can be found by using weighted similarity distance measure formula given in Section 3.Then,

Step 6:Calculating the closeness coefficients of alternatives.

Step 7:Ranking the alternatives.
The highest value of closeness coefficientsCCi,the best alternativeAiis.
§6.Illustrative of the proposed method and comparative analysis
In this part,we first give a numerical example of the low carbon logistics service provider selection problem provided by Chen et al.[6].There are three DMs(D1,D2,D3)to evaluate with four alternativesAi(i=1,2,3)and three attributes:C1:low-carbon technology,C2:risk factor,C3:capacity.
6.1.Illustration of the proposed approach
The complete MCGDM model tangent similarity measure is summarized by the following steps:
Step 1:Evaluation of alternatives for each criteria by the linguistic terms shown in Table 1.Tables 2-4 show their evaluations matrix.
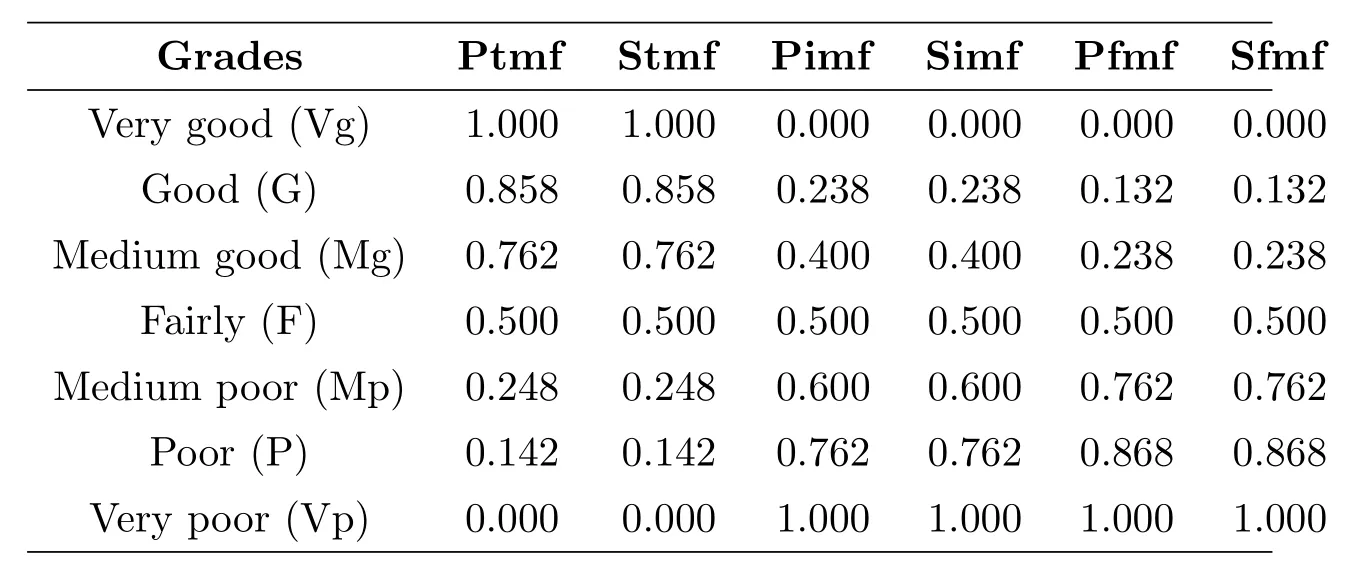
Table 1 Evaluations of the alternatives by the linguistic variables.

Table 2 Linguistic decision matrix by Decision maker D1.

Table 3 Linguistic decision matrix by Decision maker D2.


Table 4 Linguistic decision matrix by Decision maker D3.

Step 2:Determination of the aggregating decision matrixB=(bij)k×s.
Assume that the weights of the experts areδ1=0.36,δ2=0.29 andδ3=0.35,respectively.Bmatrix can be constructed.For example

Using the same way,we can calculate other values in B matrix as follows:

Step 3:Determination of the ideal solution.By using the aggregating matrix,the T2SVN local positive ideal solution(T2SVNPIS)and the T2SVN negative ideal solution(T2SVNNIS)are obtained as follows:

Step 4:Determination of the attribute weightsωby entropy.
By using Equation(4.2),the weights of the attribute can be calculated:ω=[ω1,ω2,ω3]=[0.7909,0.1213,0.0878]
Step 5:Determination of separation measures from ideal solutions to each alternatives and relative closeness coefficient.
By Equation(5.5),the separation measuresd*ianddiare indicated.Relative closeness coefficientCCiis calculated by using Equation(5.6).lets say thatλ=0.55.These results are listed in Table 5.

Table 5 Distance measure and relative closeness coefficient of each alternative.
Step 6:Ranking of the three alternatives.
According to Table 5,we can get the final ranking of three alternatives,which isA1﹥A2﹥A3.Thus,A1is the best alternative.
6.2.Comparative analysis and discussion
From Table 5,we know thatA1is the best alternative for different values ofλ.However,the ranking results are different.For confirming the reasonableness and feasibility of the proposed method,we will compare with current methods to solve the same decision-making problem.The ranking results from other methods are shown in Table 6.Ranking results from proposed method withλ=0.10,0.25,0.40 are the same as the ranking result of Mondal,s method[23].Ranking results from proposed method withλ=0.55,0.70,0.90 are the same as the ranking result of Karaaslan,s method[16]and Sahin,s method[28],which are able to show that the proposed approach is practical and effective.

Table 6 Comparison of other methods.
§7.Conclusion
In this paper,we proposed the concepts of SVNS and T2SVNS.Then,we de fined tangent similarity measure,which are also proved in T2SVN environment.We also defined a new entropy function for determining unknown attribute weights.A new approach for solving the(MCGDM)problems under T2SVNSenvironment was developed.Finally,we provided an illustrative example to illustrate the application of the proposed method.The comparative analysis with the current methods were given to confirm the rationality and feasibility of the proposed method.It enriches and develops the theory and method of MCGDM,and provides a new way to solve MCGDM problem.In future research,we will further develop the proposed similarity measures of the T2SVNS and their application.
Acknowledgements
The authors wish to thank the editors and referees for their valuable guidance and support in improving the quality of this paper.
 Chinese Quarterly Journal of Mathematics2021年2期
Chinese Quarterly Journal of Mathematics2021年2期
- Chinese Quarterly Journal of Mathematics的其它文章
- The Conjugate Gradient Method in Random Variables
- Neighborhood-Based Set-Valued Double-Quantitative Rough Sets
- AOR Iterative Method for Coupled Lyapunov Matrix Equations
- Nonexistence of Global Solutions for a Semilinear Double-Wave Equation with Nonlinearity of Derivative Type
- A Hovey Triple Arising from a Frobenius Pair
- A New Non-Parameter Filled Function for Global Optimization Problems
