Nonexistence of Global Solutions for a Semilinear Double-Wave Equation with Nonlinearity of Derivative Type

(1.College of Data Science,Guangzhou Huashang College,Guangzhou 511300,China;2.Department of Applied Mathematics,Guangdong University of Finance,Guangzhou 510521,China)

Abstract:In this paper,we study the blow-up of solutions to a semilinear double-wave equation with nonlinearity of derivative type.By using the iteration method and the differential inequality techniques,we can get the estimates of the lifespan and the blow-up of solutions in the subcritical case under some assumptions.

Keywords:Semilinear double-wave equation;Blow-up;Nonlinearity of derivative type;Lifespan estimate

§1.Introduction

In the past few years,the Cauchy problem for the semilinear wave equatio ns with nonlinearity of derivative type has been caught much attention(see[1,11–13,24–26,28,29]).There are some papers studying the following Cauchy problems

wherep＞1,n≥1 andu=u(t,x)∈Ris a scalar function denoting the displacement.Here,ε＞0 is a parameter describing the size of initial data.For(1.1),the critical exponent means Glassey exponent.Besides,the lifespan estimates of local solutions to(1.1)were obtained,namely,

Furthermore,here we point out that(1.1)is the special case of the following Moore-Gibson-Thompson(MGT)equations

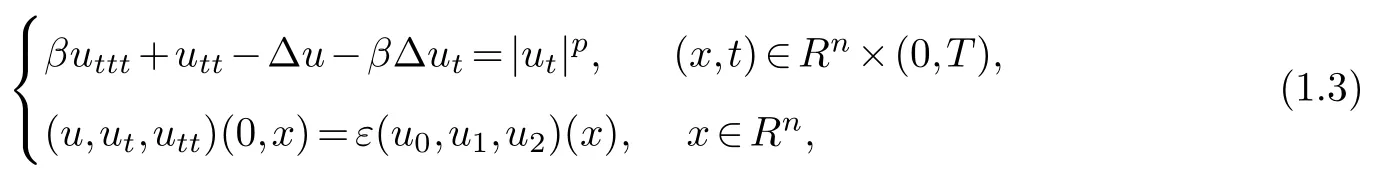
which was investigated by Chen and Palmieri[6].And they considered the subcritical case 1＜p＜pGla(n)and the critical casep=pGla(n)and obtained the blow-up result as follows by using an iteration argument

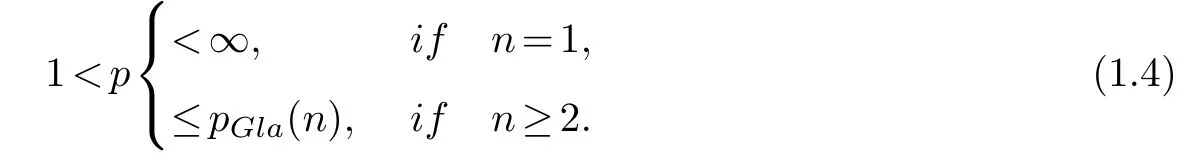
More papers about the investigation on semilinear hyperbolic equations can been seen[2,3,5,7–9,14,15,22,23]and the references cited therein.As for the study on the blow-up problem for the other PDEs,papers[4,10,16–20,27]and references cited therein can been seen.Up to the author’s knowledge,there have been no papers studying the blow-up for the Cauchy problem of double-wave equations with nonlinearity of derivative type mainly because of its high orders.For the lower order equation,we can get the result for the blow-up by Kato’s lemma and differential inequalities methods,which are not suitable for high order equations.

In this paper,we consider the following semilinear double-wave equation

wherep＞1 and the operator can be expanded by.

In order to deduce the blow-up condition and lifespan estimates for the solutions to the Cauchy problem(1.5)in the subcritical case,we have to seek new methods.Obviously,it is different from the previous studies on(1.1).And the difference demonstrates not only its big calculation but also the choosing of the energy function.Because the investigation on the blow-up for the Cauchy problem of double-wave equations with nonlinearity of derivative type is a completely open problem,so it is challenging and meaningful.Finally,we solve the problem by using iteration procedures and obtain a new blow-up result which will be deduced later.

First we define the energy solution to the Cauchy problem(1.5).

Definition 1.1.Let(u0,u1,u2,u3)∈H3(Rn)×H2(Rn)×H1(Rn)×L2(Rn).We say that u is an energy solution of(1.5)on[0,T)if

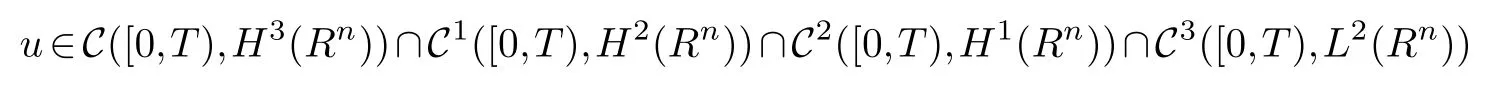
such that u∈([0,T)×Rn)satisfies(u0,u1,u2,u3)in H3(Rn)×H2(Rn)×H1(Rn)×L2(Rn)and the integral relations

for anyφ(t,x)∈([0,T)×Rn)and any t∈(0,T).

Upon integrating by parts in(1.6),we have

Lettingt→T,we can find thatusatisfies the definition of weak solution to(1.5).

In this paper,we will prove the following result:

Theorem 1.1.Let us consider p＞1such that

where the exponent p0(n)is given by

Let(u0,u1,u2,u3)∈H3(Rn)×H2(Rn)×H1(Rn)×L2(Rn)be nonnegative and compactly supported functions with supports contained inBRfor someR＞0 such thatu0oru1oru2oru3is not identically zero.Particularly,we assumeu3(x)+u2(x)＞u1(x)+u0(x).Ifuis the energy solution to(1.5)with lifespanT(ε)satisfying suppu(t,·)⊂Bt+Rfor anyt∈(0,T),there exists a positive constantε0=ε0(u0,u1,u2,u3,n,p,R),such that the solutionublows up in finite time whenε∈(0,ε0].Furthermore,we can get the upper bound estimate for the lifespan,that is

§2.Upper bound estimate for the blow-up time

In order to get the result in this paper,firstly we consider a function as follows:

whichΦis a positive smooth function satisfying the following properties

Next,we define a function with separate variablesΨ=Ψ(t,x)=e-tΦ(x).ThenΨis the solution to(-Δ)2Ψ(t,x)=0.Making use of the asymptotic behavior ofΨ,we can get that there exists a constantC1=C1(n,R)＞0 satisfying

And,applyingΨas a test function to(1.6),we get for anyt∈(0,T)

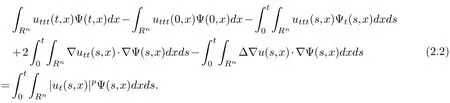
Integrating(2.2)by parts and taking attention to the properties ofΨ,we have

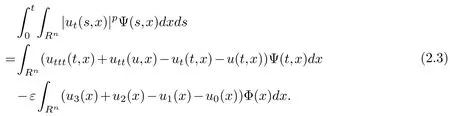
Let

Then,(2.3)can be rewritten as

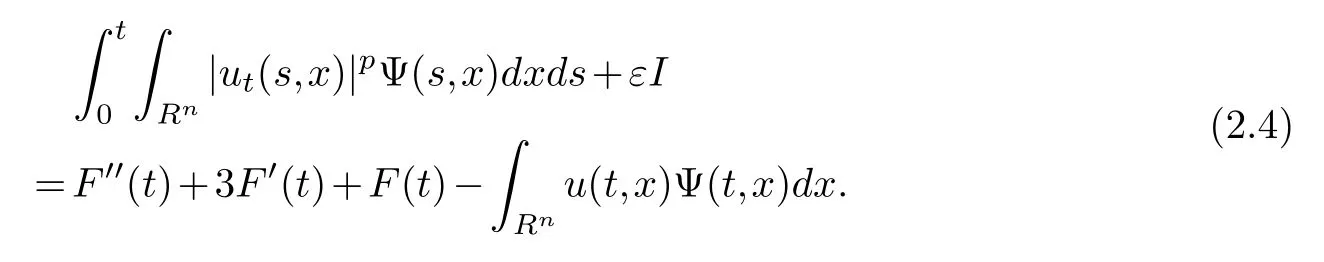
Differentiating(2.4),we obtain

Adding up(2.4)with(2.5),we get

Furthermore,let us set

Then,applying differentiation to(2.7),we have

Combining(2.7)and(2.8)and noticing(2.6),we arrive at

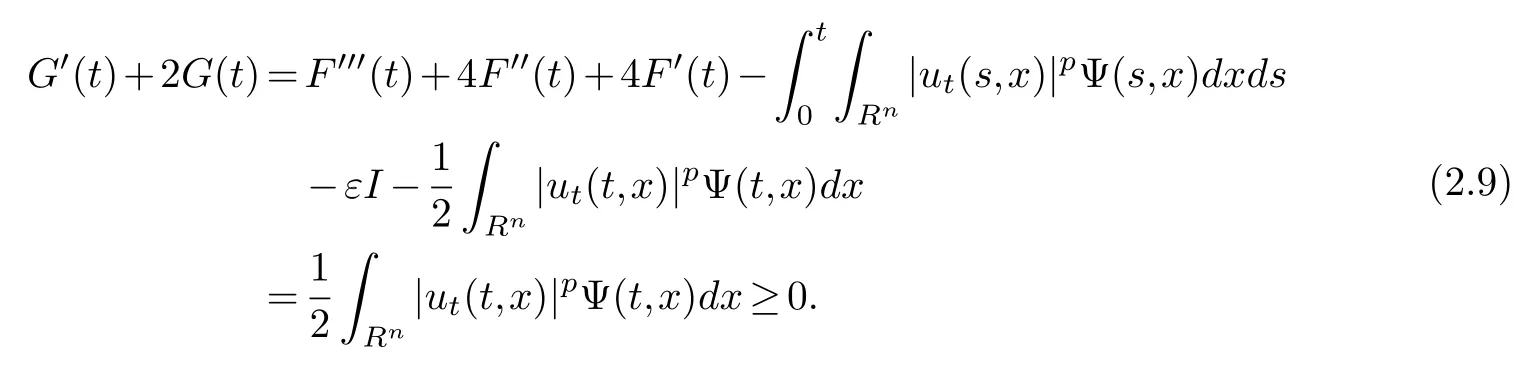
From(2.9),we can deduce

whereG(0)=[u3(x)+u0(x)-u1(x)-u2(x)]Φ(x)dx≥0.

Besides,(2.7)leads to

whereH(t)=

Obviously,it is easy to get from(2.10)

which leads to

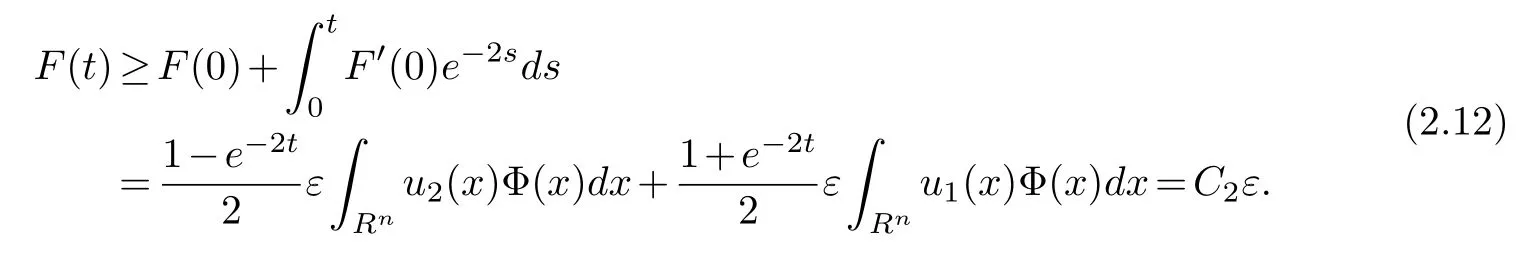
Here,we can choose suitable nonnegative functionu2(x)oru1(x)such thatC2＞0.

In addition,it follows from(2.10)

So,we can obtain from above discussions

Because of the definition ofH(t)and the H¨older’s inequality,we have

Integrating(2.14),it is easy to get

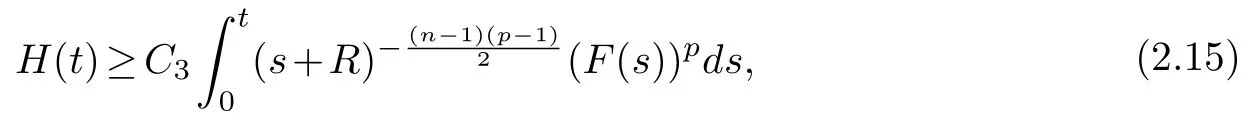
where.

Combining(2.13)and(2.15),we have

Besides,using(2.12)and(2.16),we obtain

wheret≥1.

We rewrite(2.17)as

where,β0=2,t≥1.

Next,we are going to deduce a first lower bound ofF(t)from(2.16)by the iteration argument methods.That is,we need to prove

wheret≥Lj,{Kj}j∈N,{αj}j∈Nand{βj}j∈Nare sequences of nonnegative real numbers determined later and{Nj}j∈Nis the sequence of the partial products of the infinite product

in other words,

It is easy to find(2.19)implies(2.18)forj=0.And we will prove(2.19)holds for allj≥0 by mathematical inductive methods.First,from(2.19)we can get it holds forj=0.So,the next step which is the most important one,is to prove that it holds forj+1.

Combining(2.16)and(2.19),we can deduce

Paying attention to the definition ofLj+1andlj+1and(2.20),we have

Because ofs≥Lj+1≥lj+1＞1,we can easily estimate

So,using(2.21)and(2.22),we obtain

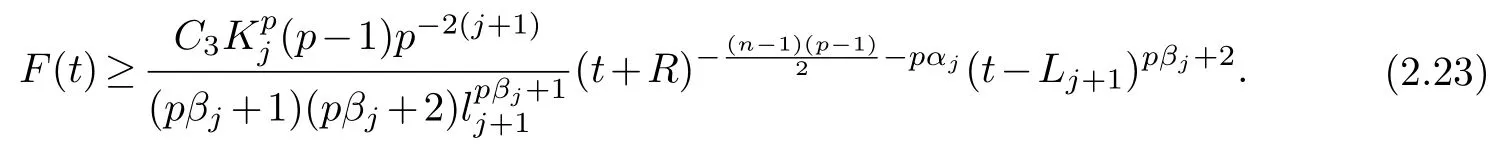
From(2.23),it shows that(2.19)holds forj+1.

Let us set

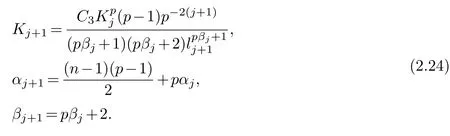
By the recursive methods,we can deduce

Meanwhile,since(pβj-1)(pβj-1+2)≤(pβj-1+2)2=and,we have

According to the definition oflj,we get

Thus,we can find a suitable positive constantM＞0 satisfying≥M,forj∈N.From above discussions,we get

whereD=C3(p-1)M(β0+)-2.

By using logarithmic functions to(2.26),we have

Letj0∈Nbe the smallest nonnegative integer,such that

Then,for anyj≥j0,we deduce from(2.27)

Let∈R,due tolj＞1,it holdsLj↑Lasj→∞.Specially,(2.19)holds forj∈Nandt≥L.Combining(2.19)and(2.28),we obtain

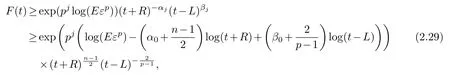
for anyj≥j0andt≥L.So,whent≥max{R,2L},we can deduceR+t≤2tandt-L≥.Then,we have

whereEandj≥j0.

In(2.30),the exponent oftis

Let us fixε0=ε0(u0,u1,u2,u3,n,p,R)＞0,such that

Then,forε∈(0,ε0],t＞andE2=,we have

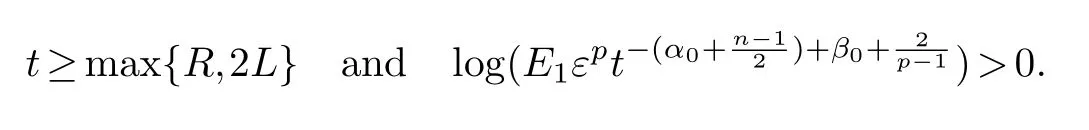
We find that for 1＜p＜p0(n)(specially,1＜pwhenn=1),exponent oftis positive.Lettingj→∞in(2.30),we can find the lower bound forF(t)blows up whenε∈(0,ε0]andt＞.Therefore,F(t)may not be finite.It shows that there exist not global solution for(1.5)in time.Furthermore,the lifespan of the local in time ofucan be estimated as follows

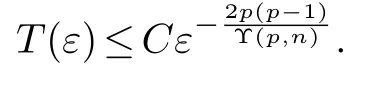
The proof is completed.

Acknowledgements

The authors express their heartfelt thanks to the editors and referees who have provided some important suggestions.