A Hovey Triple Arising from a Frobenius Pair
(College of Information Processing and Control Engineering,Lanzhou Petrochemical Polytechnic,Lanzhou 730060,China)
Abstract:We revisit Auslander-Buchweitz approximation theory and find some relations with cotorsion pairs and model category structures.From the notion of weak-cogenerators,we introduce the concept of Frobenius pair(X,ω)in a triangulated category T.We show how to construct from a Frobenius pair(X,ω)a triangulated model structure on X∧.
Keywords:Triangulated category;Weak-cogenerator;Approximation theory;Frobenius pair;Model category structures
§1.Introduction
The approximation theory has its origin with the concept of injective envelopes described by Eckmann and Schopf in 1953,and it has had a wide development in the context of module categories since the fifties(see,for example[3,4,6]).Inspired by the ideas of injective envelopes and projective covers,Auslander and Buchweitz[2]studied in the maximal Cohen-Macaulay approximations for certain modules.Since the appearance of their work,it has influenced numerous subsequent works of researchers.For example,Hern´andez and his co-authors[9]developed in an analogous theory of approximations in the sense of Auslander and Buchweitz for triangulated categories.In recent years,a powerful machinery for producing approximations via complete cotorsion pairs has been developed by Eklof,Trlifaj,Enochs,Jenda and G¨obel in[6–8].
Recall that a model category structure is a way of formally introducing homotopy theory into a category on an abelian category.Model structures are usually not constructed for their own sake but to understand the localization of a given category.The fundamental theorem in this respect is[10,Theorem 1.2.10],which shows that the localization of the category is equivalent to a sub-quotient of it.Although the category is assumed to be bicomplete,the full strength of the assumption is not used.Many authors have done research on model category structures,(see[12,13,15,18]).Hovey[11]made a general study of Quillen model structures and gave a method of constructing model structures on abelian categories.Gillespie[14]defined model structures on exact categories and got Hovey’s one-to-one correspondence between exact model structures and complete cotorsion pairs,and later generalized by Yang in[17]for triangulated categories.
The main purpose of this paper is to use Auslander-Buchweitz approximation theory in order to develop the theory of Frobenius pairs in triangulated categoriesT,which are concepts we will construct from the notions of generators and cogenerators.We will use Frobenius pairs to construct relative cotorsion pairs,seeking to bring the Hovey correspondence between complete cotorsion pairs and model structures.Specifically,from a certain type of Frobenius pair(X,ω)inT,we will obtain model category structures on the thick subcategoryX∧⊆Tof objects inTwith finite resolution dimension relative toX.
This paper is organized as follows.
In Section 2,We recalling some results from Auslander-Buchweitz approximation theory in[9].We also present in Definition 2.1 the notion of Frobenius pair,which constitutes the main subject studied in this work.
In Section 3,we recall the concept of cotorsion pairs in triangulated categories.In the particular case whereS⊆Tis a thick subcategory,a complete cotorsion pair inSis what we will call in Definition 3.1 anS-cotorsion pair.Motivated by the interplay between cotorsion pairs and model categories,we show how to obtain from a strong Frobenius pair(X,ω)two compatible and complete cotorsion pairs in the subcategoryS=X∧,which are examples of relative cotorsion pairs.
In Section 4,We apply the Hovey correspondence to obtain in Theorem 4.2 the main result in this paper:the model structure associated to(X,ω),that is,a triangulated model structure on the triangulated subcategoryX∧⊆T,whose classes of cofibrant,fibrant and trivial objects are given byX,X∧andω∧,respectively.
§2.Preliminaries
We start this section by collecting all the background material that will be necessary in the sequel.First,we recall the notions of relative projective dimension and resolution dimension of a given class of objects in a triangulated categoryT.Later,we also recall definitions and basic properties we need from Auslander-Buchweitz approximation theory.In all that follows,we are taking as the main reference for consulting approximation theory the paper[9]by Hern´andez and his coauthors.
2.1.Basic definitions
Throughout this paper,Twill be a triangulated category and[1]:T→Tits suspension functor.The term subcategory,in this paper,means a subcategory which is full,additive,and closed under isomorphisms.
LetXandYbe classes of objects inT.We put⊥X:={Z∈T|HomT(Z,-)|X=0}andX⊥:={Z∈T|HomT(-,Z)|X=0}.We denote byX*Ythe class of objectsZ∈Tfor which exists a distinguished triangleX→Z→Y→X[1]inTwithX∈XandY∈Y.Furthermore,it is said thatXisclosed under extensionsifX*X⊆X.
Recall that a classXof objects inTis said to besuspended(respectively,cosuspended)ifX[1]⊆X(respectively,X[-1]⊆X)andXis closed under extensions.
Given a classXof objects inT,it is said thatXisclosed under conesif for any distinguished triangleA→B→C→A[1]inTwithA,B∈Xwe have thatC∈X.Similarly,Xisclosed under coconesif for any distinguished triangleA→B→C→A[1]inTwithB,C∈Xwe have thatA∈X.We denote byUX(respectively,X U)the smallest suspended(respectively,cosuspended)subcategory ofTcontaining the classX.Note that ifXis suspended(respectively,cosuspended)subcategoryofT,thenX=UX(respectively,X=X U).We also recall that a subcategoryAofT,which is suspended and cosuspended,is calledtriangulated subcategoryofT.Athick subcategoryofTis a triangulated subcategory ofTwhich is closed under direct summands inT.We also denote by△T(X)(respectively,(X))to the smallest triangulated (respectively,smallest thick)subcategory ofTcontaining the classX.
Resolution and coresolution dimensionsLetXbe a class of objects inT.For any natural numbern,we introduce inductively the class(X)as follows:(X):=Xand assuming defined(X),the class(X)is given by all the objectsZ∈Tfor which there exists a distinguished triangleZ[-1]→W→X→ZinTwithWandX∈X.
LetXbe a class of objects inTandMan object inT.
(1)X∧:=(X)andX∨:=(X).
(2)TheX-resolution dimensionofMisresdimX(M):=min{n∈N|M∈(X)}.Dually,theX-coresolution dimensionofMiscoresdimX(M):=min{n∈N|M∈(X)}.
(3)For any subclassYofT,we set resdimX(Y):=sup{resdimX(M)|M∈Y}.Similarly,we also have coresdimX(Y).
Remark 2.1.(1)Observe that a suspended class U of T is closed under cones.Similarly,if U is cosuspended then it is closed under cocones.
(2)Let(Y,ω)be a pair of classes of objects in T withω⊆Y.If Y is closed under cones(respectively,cocones),thenω∧⊆Y(respectively,ω∨⊆Y).
Relative homological dimensions and weak-cogeneratorsLetXbe a class of objects inTandMan object inT.
(1)TheX-projective dimensionofMis
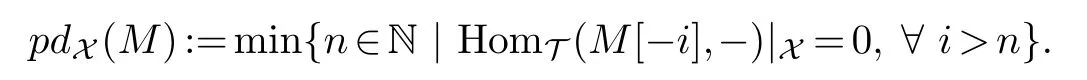
(2)TheX-injective dimensionofMis

(3)For any classYof objects inT,we set

Let(X,ω)be a pair of classes of objects inT.We say thatωis aweak-cogeneratorinX,ifω⊆X⊆X[-1]*ω;ωis aweak-generatorinX,ifω⊆X⊆ω*X[1];ωisX-injectiveifidX(ω)=0;and dually,ωisX-projectiveifpdX(ω)=0.
Proper class of triangles andξ-projectiveA classξ⊆△is called aproper class of trianglesif the following conditions hold:
(1)ξis closed under isomorphisms,finite coproducts and△0⊆ξ⊆△.
(2)ξis closed under suspensions and is saturated.
(3)ξis closed under base and cobase change.
It is known that△0and the class of all triangles△inTare proper classes of triangles.There are more interesting example of proper classes of triangles enumerated in[5,Example 2.3].Throughout the paper,we fix a proper class of trianglesξin the triangulated categoryT.
Recall that an objectP∈T(resp.,I∈T))is calledξ-projective(resp.,ξ-injective)if for any triangleA→B→C→ΣAinξ,the induced sequence of abelian groups 0→HomT(P,A)→HomT(P,B)→HomT(P,C)→0(resp.,0→HomT(C,I)→HomT(B,I)→HomT(A,I)→0)is exact.
The symbolP(ξ)(resp.I(ξ))will denote the full subcategory ofξ-projective(ξ-injective)objects ofT.As an immediate consequence of the above definition we have that the categoriesP(ξ)andI(ξ)are full,additive,closed under isomorphisms,direct summands,andΣ-stable.Tis said to haveenoughξ-projectives(resp.,ξ-injectives)if for any objectsX∈Tthere exists a triangleK→P→X→K[1]inξ(resp.,X→I→L→X[1]inξ)withP∈P(ξ)(resp.,I∈I(ξ)).
2.2.Fundamental results from Auslander-Buchweitz approximation theory
Keeping in mind the terminology and notation we have presented so far,we are ready to recall the necessary background from Auslander-Buchweitz approximation theory.
Definition 2.1.Let X andωbe two subcategories of T.We say that(X,ω)is a Frobenius pair in T if the following three conditions are satisfied:
(1)X is thick,that is,X=(X).
(2)ωis closed under direct summands in T.
(3)ωis an X-injective weak-cogenerator in X.
If in addition,ωis also anX-projective weak-generator inX,then we say that(X,ω)is astrong Frobenius pairinT.
The proof of the following results can be found in Hern´andez and his co-authors[9,section 3 and section 5].
Theorem 2.1.[9,Theorem 3.5]Let X⊆T be a cosuspended subcategory andω⊆T be an X-injective weak-cogenerator in X.Then,the following conditions hold true:
(1)X∧=△T(X).
(2)If X are closed under direct summands,then X∧=(X).
In particular,If(X,ω)is a Frobenius pair,then X∧=(X).
Proposition 2.1.[9,Proposition 5.2,5.3]Let X andωbe two subcategories of T such thatω is X-injective.Then,the following conditions hold true:
(1)ω∧is X-injective.
(2)If in additionωis a weak-cogenerator in X which is closed under direct summands in T,then the following equalities hold:
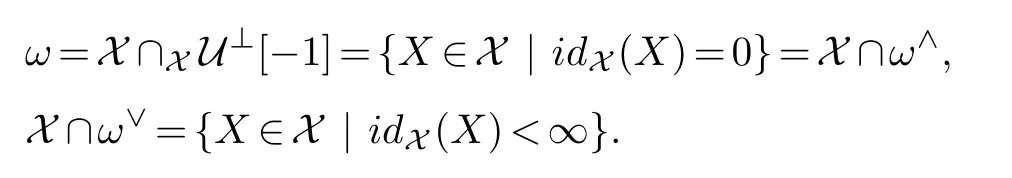
Furthermore,we have that idX(M)=coresdimω(M),for every M∈X∩ω∨.
Asadollahi and Salarian definedξ-Gorenstein projective andξ-Gorenstein injective objects in[1].We denoteξ-Gorenstein projective(ξ-Gorenstein injective)objects byGP(ξ)(GI(ξ)).
Example 2.1.Let T has enoughξ-projectives.Then the pair(GP(ξ),P(ξ))satisfies thehypothesis in Proposition2.1.So part(1)implies that idGP(ξ)(P(ξ)∧)=0.Note also thatP(ξ)∧=,the class of objects with finiteξ-projective dimension.By[1,Proposition 3.19],we get the first result in the above proposition.On the other hand,[1,Theorem 3.17]impliesthe second result.
Theorem 2.2.[9,Theorem 5.4]Let(X,ω)be a pair of classes of objects in a triangulated category T such that X is closed under extensions andωis a weak-cogenerator in X.Then,the following statements hold.
(1)For all C∈(X),there exist two distinguished triangles in T:

(2)Ifωis X-injective,thenφC is a right X-approximation,andφC is a leftω∧-approximation.
Corollary 2.1.Let X andωbe two subcategories of T such that X is closed under extensions and direct summands in T,andωis a weak-cogenerator in X.If resdimX(C)≤1and C∈⊥ω[1],then C∈X.
Proof.For everyC∈⊥ω[1]withresdimX(C)≤1,by Theorem 2.2,we have a triangleC[-1]→W→X→CwithW∈ωandX∈X,which is split sinceC∈⊥ω[1].Hence,C∈XsinceXis closed under direct summands.
Theorem 2.3.[9,Theorem 5.6]Let(X,ω)be a pair of classes of objects in T which are closed under direct summands in T.If X is closed under extensions andωis an X-injective weak-cogenerator in X,then

Example 2.2.Let T has enoughξ-projectives.By Theorem2.3,we have that for every object M with finiteξ-G projective dimention

In other words,we have that the following conditions are equivalent:
(1)ξ-Gpd(M)≤n.
This was proven by Asadollahi and Salarian in[1,Proposition 3.19].
Proposition 2.2.[9,Propositin 5.9]Let(X,ω)be a pair of classes of objects in T such thatω is closed under direct summands in T and X is cosuspended category in T.Ifωis an X-injective weak-cogenerator in X,Thenω∧=X∧∩X⊥[-1].
Proposition 2.3.Let(X,ω)be a Frobenius pair in T.Then X∧∩⊥(ω[n+1])=X=X∧∩⊥(ω∧[n+1])for any n≥0.
Proof.By Proposition 2.1,we know thatX⊆⊥(ω[n+1])andX⊆⊥(ω∧[n+1]),then we haveX⊆X∧∩⊥(ω[n+1])andX⊆X∧∩⊥(ω∧[n+1]).We assert thatX∧∩⊥(ω∧[n+1])⊆X.Indeed,letC∈X∧∩⊥(ω∧[n+1]).Then,by Theorem 2.2,there exists a distingusished triangle
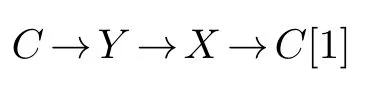
whereX∈X⊆⊥(ω∧[n+1])andY∈ω∧.SinceC∈⊥(ω∧[n+1]),it follows thatY∈⊥(ω∧[n+1]).Now using Theorem 2.3,we get thatresdimX(Y)=pdω∧(Y)=0,and thusY∈X.Hence,C∈XsinceXis cosuspended.The inclusionX∧∩⊥(ω[n+1])⊆Xfollows similarly.
Theorem 2.4.[9,Theorem 5.16]Let(X,ω)be a pair of classes of objects in T,X be cosuspended andωbe closed under direct summands in T.Ifωis an X-injective weak-cogenerator in X,the following statements hold.
(1)(ω∧)∨={C∈X∧|idX(C)<∞}.
(2)If X is closed under direct summands in T,then(ω∧)∨=(ω).
Theorem 2.5.Let X⊆T be a thick subcategory of T,and Y⊆T be a thick subcategory of T contained in X∧,such thatω:=X∩Y is an X-injective weak-cogenerator in X.Then,the following equalities hold:

Moreover,if{C∈X∧∩ω⊥[-1]|idX(C)≤1},then the above include relationship can be changed to an equation.
Proof.We split the proof into several parts.
·By Proposition 2.2,we have the equalityω∧=X∧∩X⊥[-1].
·We now show thatω∧=Y.Indeed,sinceω⊆Y,By Remark 2.1,we have thatω∧⊆Y.Now letY∈Y.Knowing thatY⊆X∧,we get a distinguished triangle in Theorem 2.2,sayY[-1]→K→X→YwithX∈XandK∈ω∧⊆Y.SinceYis closed under extensions,we have thatX∈X∩Y=ω.It follows thatY∈ω∧,that is,Y⊆ω∧.So far,we have proven the equalitiesY=ω∧=X∧∩X⊥[-1].
·By[9,Proposition 5.9],we have the equalityX∧∩X⊥[-1]=X∧∩X U⊥[-1].
·It is only left to prove the equalityY⊆{C∈X∧∩ω⊥[-1]|idX(C)<∞}.Note that we already haveY⊆X⊥[-1]⊆ω⊥[-1],and by the equality in Theorem 2.4 we know thatY=ω∧⊆(ω∧)∨={C∈X∧|idX(C)<∞}.So it follows that the containmentY⊆{C∈X∧∩ω⊥[-1]|idX(C)<∞}holds.
Now consider an objectM∈X∧∩ω⊥[-1]withidX(M)≤1.GivenX∈X,there is a distinguished triangleX→W→X′→X[1]withW∈ωandX′∈X.Then,we have an induced sequence HomT(W[-1],M)→HomT(X[-1],M)→HomT(X′[-2],M)of abelian groups where HomT(W[-1],M)=0 sinceM∈ω⊥[-1],and HomT(X′[-2],M)=0 sinceidX(M)≤1.It follows thatM∈X∧∩X U⊥[-1]=Y.
§3.Relative cotorsion pair
This section is devoted to present the notion of cotorsion pairs relative to a thick subcategorySof a triangulated categoryTwith respect toξ.We begin this section recalling the concept of cotorsion pairs in triangulated categories,and then we introduce the relativeS-cotorsion pairs as complete cotorsion pairs inS⊆T.Later,we provide a characterization for this concept which,along with the results presented in Section 2,allows us to construct relative cotorsion pairs from Frobenius pairs.
3.1.Cotorsion pairs in triangulated categories
Bare’s theory[5,Definition 2.4]LetT:be a triangle inξ.We callh:CΣAthe characteristic class of△,and usually we denote it bychT=h.LetA,Cbe two objects ofT,and consider the classξ*(C,A)of all trianglesAinξ.we define a relation inξ*(C,A)as follows:IfTi:,i=1,2,are elements ofξ*(C,A),then we defineT1~T2if there exists morphism of triangles:Obviously,αis an isomorphism
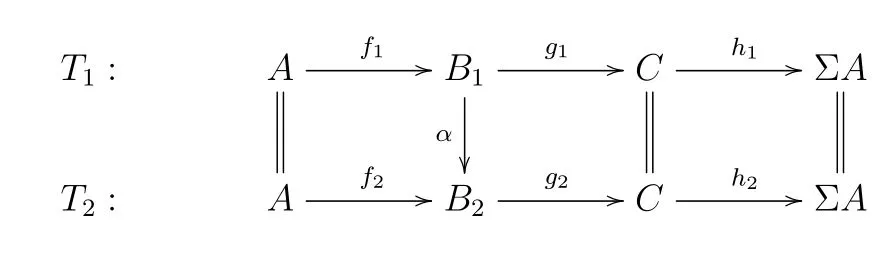
and~is an equivalence relation on the classξ*(C,A).Using base and cobase change,it is easy to see that we can define(as in the case of the classical Bare’s theory in an abelian category)a sum in the classξ(C,A):=ξ*(C,A)/~in such a way thatξ(C,A)becomes an abelian group andξ(-,-):T op×T→Abbecomes an additive bifunctor.Trivially,we havech,which is an isomorphism of bifunctors:ξ(-,-)→Phξ(-,Σ-).
Definition 3.1.[17,Definition 2.6]A pair of classes(A,B)in a triangulated category T is a cotorsion pair with respect toξif the following conditions hold:
(1)ξ(A,B)=0for all A∈A and B∈B.
(2)ξ(A,C)=0for all A∈A,then C∈B.
(3)ξ(C,B)=0for all B∈B,then C∈A.
For convenience,B that satisfies(1)and(2)is denoted as A⊥,ξ,A that satisfies(1)and(3)is denoted as⊥,ξB.
A cotorsion pair(A,B)with respect toξis said to have enoughξ-projectives if for anyT∈Tthere is a triangleB→A→T→ΣBinξwhereA∈AandB∈B.We say it has enoughξ-injectives if for anyT∈Tthere is a triangleT→B→A→ΣTinξ,whereA∈AandB∈B.If both of these hold,we say that(A,B)is acompletecotorsion pair with respect toξ.
3.2.Cotorsion pairs relative to thick subcategories
From now on,we focus on a special type of complete cotorsion pairs in a thick subcategorySof a triangulated categoryT.
Definition 3.2.Let S be a thick subcategory of a triangulated category T,and F and G be two subcategories of S(thought as a triangulated category).We say that(F,G)is a left S-cotorsion pair in T if F=⊥,ξG and if for every object S∈S there exists a distinguished triangle G→F→S→G[1]inξwith F∈F and G∈G.Similarly,we have the definitions of right S-cotorsion pair in T.Finally,by an S-cotorsion pair(F,G)in T we mean that(F,G)is both a left and right S-cotorsion pair in T.
Proposition 3.1.Let S,F and G be subcategories of T,where S is thick.Then,(F,G)is a left S-cotorsion pair in T if,and only if,the following conditions hold true:
(1)F and G are subcategories of S,and F is closed under direct summands in T.
(2)ξ(F,G)=0.
(3)For every S∈S,there exist a distinguished triangle G→F→S→G[1]inξwith F∈F and G∈G.
Proof.The”only if”part is clear.For the”if”part,suppose thatF,G⊆Tsatisfy conditions(1),(2)and(3).It is clear thatF⊆⊥,ξG.Now letS∈⊥,ξGand a distinguished triangle

as in condition(3).Then,ξ(F,G)=0,which implies that the above distinguished triangle splits.It follows thatSis a direct summand ofF∈F,and so we haveS∈Fby condition(1).Hence the inclusion⊥,ξG⊆Ffollows.
3.3.Relative cotorsion pairs from Frobenius pairs
The characterization of(left and right)S-cotorsion pairs given in Proposition 3.1 allows us to construct easily cotorsion pairs from Frobenius pairs(Recall Definition 2.1).Later on,we will study correspondences between these two notions.
Theorem 3.1.If(X,ω)is a Frobenius pair in T,then(X,ω∧)is an X∧-cotorsion pair in T.Moreover,the equalitiesω=X∩ω∧andω∧=X∧∩X⊥[-1]from Propositions2.1and2.2hold true.In particular,ω∧is a thick subcategory of T.
Proof.We check conditions(1),(2)and(3)in Proposition 3.1,along with their dual statements,to show that(X,ω∧)is anX∧-cotorsion pair inT.By Theorem 2.1,X∧⊆Tis a thick subcategory.On the other hand,we haveidX(ω∧)=idX(ω)=0 by Proposition 2.1,and so condition(2)follows.Furthermore,Proposition 2.2 gives us thatω∧=X∧∩X⊥[-1],and henceω∧is closed under direct summands.Then,the dual of condition(1)follows,while(1)holds sinceXis closed under direct summands.Note that condition(3)and its dual hold by Theorem 2.2,and hence we conclude that(X,ω∧)is anX∧-cotorsion pair inT.
Theorem 3.2.If(X,ω)is a strong Frobenius pair in T,Then,the following assertions hold true:
(a)(ω,X∧)is an X∧-cotorsion pair in T.
(b)ω∧=(ω).
Proof.For part(a),we check again conditions(1),(2)and(3)in Proposition 3.1,along with their duals statements.Conditions(1)and its dual are straight forward.To show condition(2),it suffices to use dual of[9,Lemma 4.6],[9,Lemma 4.2(b)]and the propertypdX(ω)=0,so that we have the equalitiesidω(X∧)=idω(X)=pdX(ω)=0.To show the dual of condition(3),for anyY∈X∧,since(X,ω∧)is a cotorsion pair,we have a ditinguishen triangleY→W′→X′→Y[1]withW′∈ω∧andX′∈X.ωis a weak-generator inXimplies that there exists a ditinguishen triangleX→W→X′→X[1]withW∈ωandX∈X.Then we have the following commutative diagram by base change:
The second column implies thatM∈X∧sinceW′∈ω∧⊆X∧,X∈X⊆X∧andX∧is thick.Then the distinguished triangleY→M→W→Y[1]is our needed.Finally,for(3),letY∈X∧.By Theorem 3.1,there exists a distinguished triangleW1→X1→Y→W1[1]withW1∈ω∧andX1∈X,and a distinguished triangleX2→W2→X1→X2[1]withW2∈ωandX2∈Xsinceωis a weak-generator inX.Then we have the following commutative diagram by base change:
The second row implies thatM∈X∧sinceW1∈ω∧⊆X∧,X2∈X⊆X∧andX∧is thick.Then The distinguished triangleM→W2→Y→M[1]is our needed.


We now focus on showing the equality.Indeed,by the equalities in Theorem 2.4,we have that(ω)=X∩(ω∧)∨={C∈X|idX(C)<∞}.On the one hand,by Proposition 2.1,we have the equality(ω)={C∈X|idX(C)<∞}=X∩ω∨.On the other hand,sinceωis anX-projective weak-generator inX,we can use the dual version of the equality in Proposition 2.1,that is,X∩ω∨=ω.Hence,=ωholds.SettingY:=(ω)in Theorem 2.5,it follows thatω∧=(ω).
3.4.Hereditary relative cotorsion pairs
So far we know that the concept ofS-cotorsion pair is a description of the completeness of cotorsion pairs inS.As many complete cotorsion pairs in the literature are hereditary,we will introduce in this section the corresponding property of”being strongly hereditary”forS-cotorsion pairs.We begin with the definition of hereditary cotorsion pairs.
Definition 3.3.Let(F,G)be an S-cotorsion pair in T.We say that(F,G)left strongly hereditary if F is closed under cocones in T.
SupposeThas enoughξ-projectives,ifK→P→A→K[1]is distinguished triangle withP∈P(ξ),then we call the objectKa firstξ-syzygy ofA.Annthξ-syzygy ofAis defined as usual by induction,we denote byΩi(A)theithξ-syzygy ofA.
Theorem 3.3.Let(F,G)be a left strongly hereditary S-cotorsion pair in T,and setω:=F∩G.If T has enoughξ-projectives,then the following statements hold true:
(a)F=⊥G[n+1]for any n≥0.
(b)(F,ω)is a Frobenius pair in T.
(c)(ω,G)is a Frobenius pair in T.
(d)If G⊆F∧,then(F,G)is an F∧-cotorsion pair in T.Moreover,the following equalities hold:G=ω∧=F∧∩F⊥[-1],F=F∧∩⊥(ω[1])=F∧∩⊥(ω∧[1]).
Proof.(a)For everyF∈F,G∈Gandn≥1,we have a natural isomorphismHom(F[-n-1],G)=Hom(Ωn(F)[-1],G)=0 whereΩn(F)∈FsinceFis closed under cocones inT.
(b)The subcategoryF=⊥G[1]∩Sis thick subcategory inT.On the other hand,note also thatωis closed under direct summands.So it remains to check thatωis anF-injective weak-cogenerator inT.(a)implies thatωisF-injective,sinceidF(ω)≤idF(G)=0.Now letF∈F.By the dual of condition(3)in Proposition 3.1,there exists a distinguished triangleF→W→K→F[1]inTwithW∈GandK∈F.SinceFis closed under extensions,we obtain thatW∈F∩G=:ω,proving thatωis a weak-cogenerator inF.
(c)The equalityG=F⊥[-1]∩Simplies thatGis thick subcategory inT.Thus,we have thatGis closed under cones and direct summands inT.ω:=F∩Gimplies thatωis thick subcategory inT.The rest of the proof follows as(b).
(d)We check conditions(1),(2)and(3)in Proposition 3.1,along with their dual statements,to show that(F,G)is anF∧-cotorsion pair inT.SinceF⊆SandSis closed under cones inT,By Remark 2.1,we have thatF∧⊆S.Note thatFandGare subcategories ofF∧andξS(F,G)=0,so the condition(1)and(2)follows.So everyS∈F∧has two distinguished triangles as in Theorem 2.2.Hence,(F,G)is anF∧-cotorsion pair inT.
To show the equalities,we start noting by(b)and by Theorem 3.1,the equalitiesω∧=F∧∩F⊥[-1]andF∧∩⊥(ω[1])=F=F∧∩⊥(ω∧[1]),thus having the second equality.We assert thatG=ω∧.Indeed,by Remark 2.1,we get thatω∧⊆G.And in order to prove thatG⊆ω∧,it suffices to see thatG⊆F∧∩F⊥[-1],which follows by(a),sinceG⊆F∧.Hence,the first equality also follows.
§4.Model category structures from a Frobenius pair
The concept of model category structure was introduced by[16]in 1967,which is a way of formally introducing homotopy theory into a category on an abelian category.Hovey[11]made a general study of Quillen model structures and gave a method of constructing model structures on abelian categories.Yang[17]defined model structures on triangulated categories and got Hovey’s one-to-one correspondence between triangulated model structures and complete cotorsion pairs.
In this section,given a strong Frobenius pair(X,ω)inT,we will obtain a triangle model structure onX∧.
Theorem 4.1.[17,Theorem 3.3,Theorem 4.12]Suppose T has a triangulated model structure with respect toξ.Let C denote the full subcategory of cofibrant objects,F denote the full subcategory of fibrant objects and W denote the full subcategory of trivial objects.Then:
(1)W is a thick subcategory of T.
(2)(C,F∩W)and(C∩W,F)are complete cotorsion pairs with respect toξ.
Conversely,given classes C,F and W satisfying the two conditions above,there is a unique triangulated model structure on T with respect toξsuch that W is the class of trivial objects,C is the class of cofibrant objects and F is the class of fibrant objects.
Theorem 4.2.Let(X,ω)be a strong left Frobenius pair in T.Then,there exists a unique triangulated model structure on X∧,referred as the Auslander-Buchweitz model structure associated to(X,ω),such that X is the subcategory of cofibrant objects,X∧is the subcategory of fibrant objects,andω∧is the subcategory of trivial objects.We will denote this model structure by(X,ω,X∧).
Proof.Now given a strong Frobenius pair(X,ω)in a triangulated categoryT,the triangulated subcategoryX∧⊆Tis thick.By Theorems 3.1 and 3.2,we have twoX∧-cotorsion pairs(X,ω∧)and(ω,X∧)withω=X∩ω∧.These are complete cotorsion pairs in the thick subcategoryX∧⊆T,thus forming a Hovey triple(X,ω,X∧).
§5.Conclusion
From the notion of weak-cogenerators,we introduce the concept of Frobenius pair(X,ω)in a triangulated categoryT,and then,we get anX∧-cotorsion pair(X,ω∧)from it.Finally,We show how to construct from a Frobenius pair(X,ω)a triangulated model structure onX∧.
Acknowledgements
The author is very grateful to referee for the comments,corrections and suggestions.
 Chinese Quarterly Journal of Mathematics2021年2期
Chinese Quarterly Journal of Mathematics2021年2期
- Chinese Quarterly Journal of Mathematics的其它文章
- 《数学季刊》征稿简则
- Exponential Growth of Solutions for Nonlinear Coupled Viscoelastic Wave Equations with Degenerate Nonlocal Damping and Source Terms
- Auslander Categories and Free Normalizing Extensions
- Painlev´e Analysis of Higher Order Nonlinear Evolution Equations with Variable Coefficients
- A New Non-Parameter Filled Function for Global Optimization Problems
- Entropy and Similarity Measure for T2SVNSs and Its Application
