对流层映射函数模型对CMONOC网解算精度对比分析

石 鼎，刘 磊，李永怀，刘芳芳

（1.山东中基地理信息科技有限公司，山东 济南 250000；2.内蒙古一一五地质矿产勘查开发院，内蒙古 乌兰浩特 137400；3.新疆瑞伦矿业有限责任公司，新疆 哈密市 839000）

GNSS卫星信号穿过大气层时会产生信号延迟，而80%的信号延迟发生在对流层中，对流层大气成分变化会对信号延迟影响，尤其是水汽对卫星信号的影响最为敏感。大气成分中的水汽造成的湿延迟却占对流层总延迟的10%以上[1-2]，带来严重的对流层延迟误差，电离层引起的信号延迟误差由不同频率间进行相位组合可以基本消除，而对流层中成分较为复杂，其对GNSS定位造成的误差无法完全消除，目前国内外学者大多数采用建立大气模型的方法来进行对流层延迟改正[3]，但是想要得到不同路径上的大气延迟，还需要对流层映射函数模型，映射函数可以把天顶方向的对流层产生的延迟投影到任意方向上，从而求得斜路径上的大气延迟，因此，映射函数模型的选择对于计算GNSS大气延迟是非常重要的[4]。基于此，针对不同区域选择最优的映射函数模型可以改善目标区域对流层延迟，从而提高GNSS定位的精度。

中国大陆构造环境监测网络（CMONOC）是一种服务于大地测量学、地震学、地球物理学等多学科，能够提供气象预报、地震监测的职能，应用于科学理论和应用研究、社会防灾减灾和国民经济的建设中。近年来，国内外学者开展关于映射函数在GNSS数据处理中影响方面的研究。Boehm等[5]分别对VMF1、GMF、NMF3种映射函数模型进行对流层延迟改正对比分析实验，实验结果证明使用VMF1映射函数模型比NMF和GMF映射函数模型的精度在水平方向和高程方向上分别高出3%和7%。徐杰等[6]对混合观测网GPS数据进行不同映射函数对比分析，实验结果表明在亚洲地区GMF映射函数模型比与VMF1、NMF映射函数模型表现结果更佳。李斐等[7]对南极周边IGS站的数据进行对流层映射函数对比分析，结果表明NMF映射函数模型在N、E、U 3个方向的误差均明显大于GMF和VMF1映射函数模型，VMF1效果略好于GMF映射函数模型。蒋光伟等[8-10]利用香港CORS 观测数据进行实验分析，实验结果认为基于VMF1 映射函数模型对香港CORS网解算精度表现最佳。以上实验表明，不同的映射函数在不同地区表现效果不一致，因此借助CMONOC网中GNSS观测数据，验证对流层映射函数对CMONOC网解算精度的影响。

1 对流层映射函数模型

1.1 NMF函数模型

Niell提出了基于时间周期性变化大气层分布的NMF映射函数模型，其静力学延迟映射函数反映了大气密度随高度降低而增加的变化特性，NMF映射函数模型解决了地表参数对流层延迟改正模型精度影响的问题。NMF映射函数模型是高精度GNSS数据处理软件常用的对流层映射函数模型之一，式（1）为天顶静力学延迟映射函数：

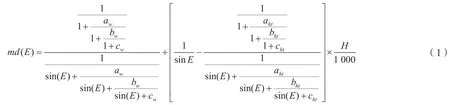
式（1）中，E是截止高度角；aht=2.53×10-3，bht=5.49×10-3，cht=1.14×10-3；H为正高。当纬度在15°～75°时，各系数可由式（2）内插求得：

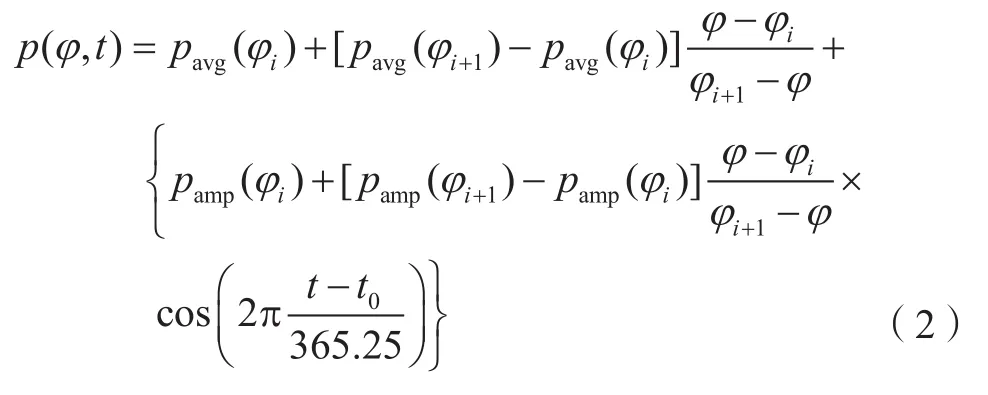
式（2）中，p表示要内插的系数；ad、bd、cd，t为年积日，t0=28为参考时刻的年积日；纬度φi和φi+1时的系数的平均值pavg和波动的幅度pamp值见表1所示。

表1 干分量投影函数系数

当测站纬度小于15°时，系数ad、bd、cd可由式（3）求得：

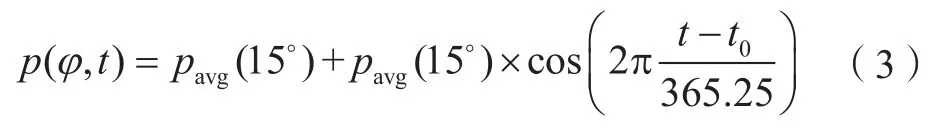
当测站纬度大于75°时，系数ad、bd、cd可由式（4）求得：

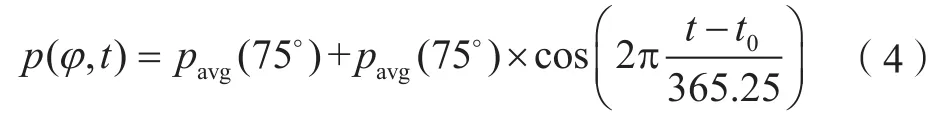
NMF模型中湿延迟映射函数为：

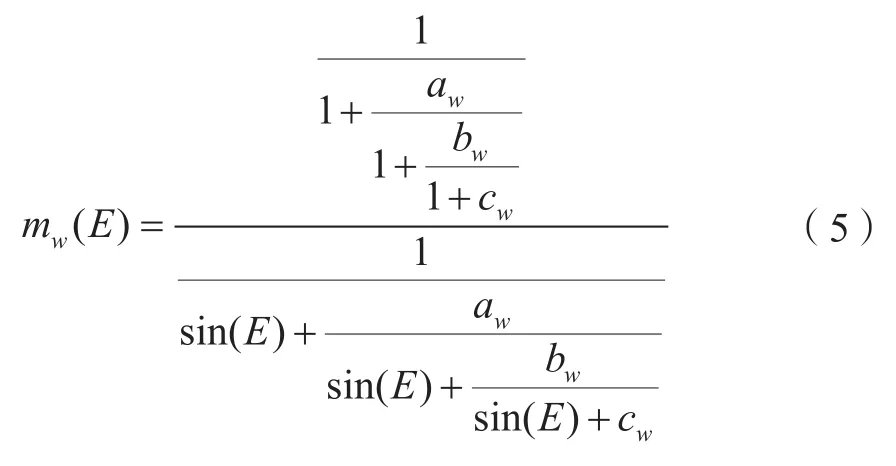
当纬度在 15°～75°时，系数ad、bd、cd可由式（6）内插求得：

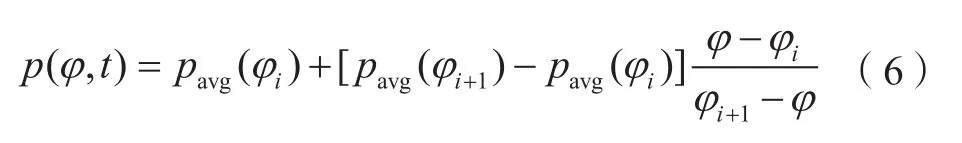
各系数见表2所示。

表2 湿分量投影函数系数

当测站纬度小于15°时，各系数取纬度等于15°时的值；当测站纬度大于75°时，各系数取纬度等于75°时的值。

1.2 VMF1函数模型

Boehm等利用数值天气计算对流层映射函数模型，创建了VMF模型。VMF模型和NMF具有相同的数学结构，VMF1模型是VMF模型经过改良后的映射函数模型。它是利用射线跟踪法得到空间分辨率为2°～2.5°时间分辨率为6 h的全球任意格网区域。在VMF1网站中提供了包括算法和格网数据在内的所有资料（http://ggosatm.hg.tuwien.ac.at/DELAY/）。VMF1映射函数模型是根据实时气象数据得到的，因此其有约34 h的时间延迟，实时性较差，但是精度较高。为了解决VMF1时延问题，Boehm提供了预报的VMF1模型VMF1-FC，以供实时用户使用。

1.3 GMF函数模型

Boehm为解决VMF1使用起来不够方便的缺点，还提供了 一种“折衷”的解决办法，参考NMF映射函数模型的方法，将地理位置信息（经纬度和高程）和年积日作为输入参数，通过内插得到对流层投影函数的系数，该模型称为GMF投影函数。它具有NMF模型的优点而且精度更好，解决了VMF1 的时延问题并与其达成很好的契合。

2 数据来源及实验流程

实验选取CMONOC网中100个观测站中观测数据质量较好的数据产品，站点分布图如图1所示，GPS原始观测数据采样间隔为30 s，精密星历及钟差产品使用IGS中心发布的事后产品（ftp://garner.ucsd.edu）。

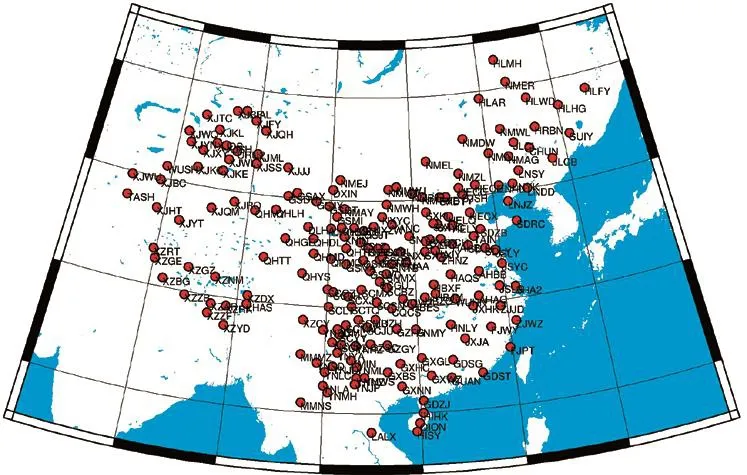
图1 站点分布图

为了比较对流层映射函数模型对CMONOC网解算精度的影响，在解算时引入IGS（BJFS站、SHAO站）作为固定站，将100个CMONOC站设置为非固定站。对GPS观测数据预处理部分采用GNSS数据预处理软件TEQC进行数据预处理，对原始观测数据进行数据格式标准化处理及质量检核分析，剔除观测质量较差的O文件。基线解算使用GAMIT软件，解算类型为松弛解，电离层选择为无电离层线性组合模式，对流层折射使用Saastamoinen模型，实验流程图如图2所示。

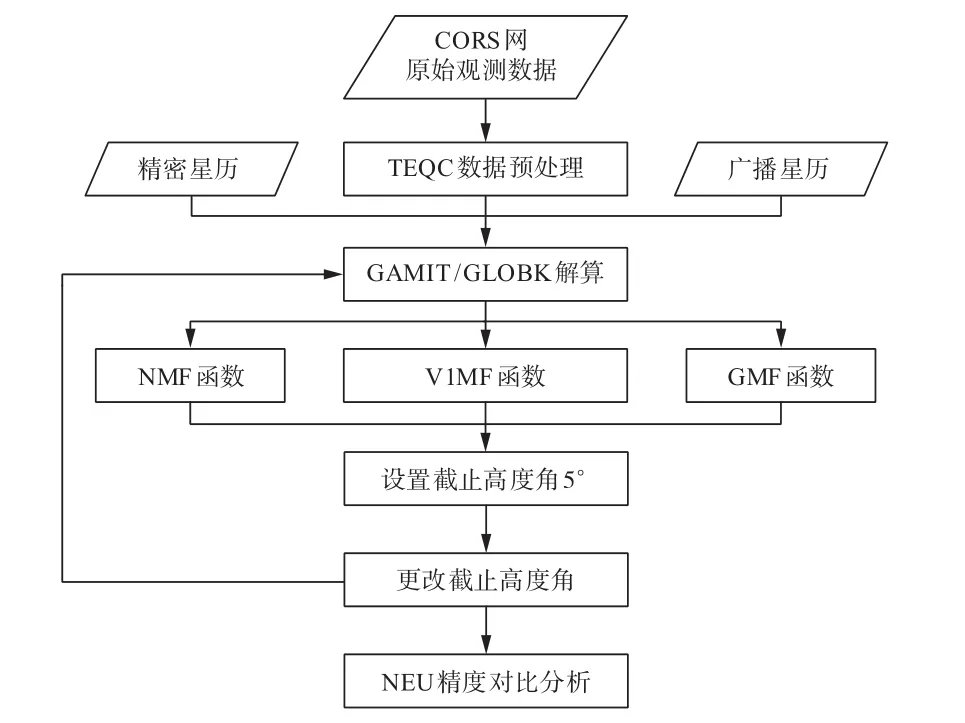
图2 实验流程图

3 结果分析

标准化均方根误差（NRMS）是GAMIT/GLOBK软件中用来表示基线解算结果中基线值偏离加权平均值的程度，一般情况下认定NRMS值越小，基线解算结果越好、精度越高，反之越差。一般情况下NRMS小于0.3，若大于0.3则认为基线解算失败，其原因可能是周跳未修复或起算坐标有误等原因，需重新解算，基线解算结果NRMS值如图3所示。

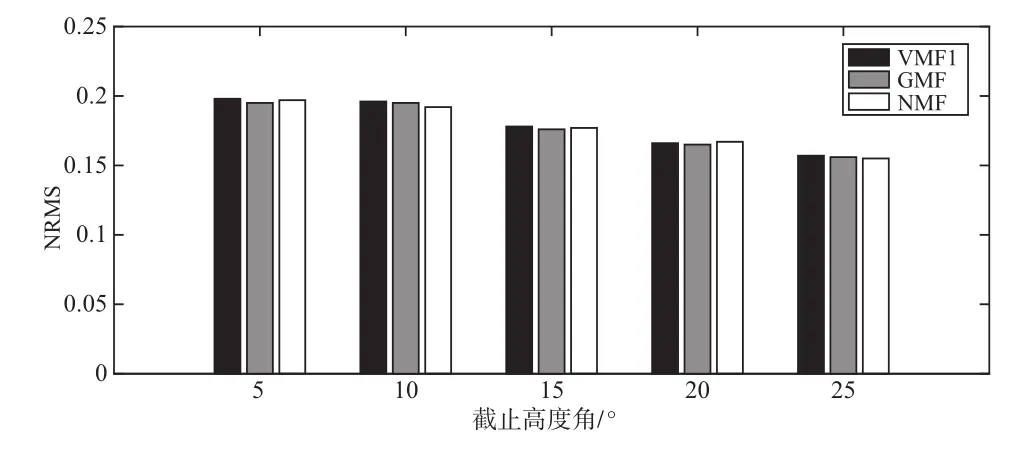
图3 GAMIT基线解算结果

由图3可知，不同截止高度角下NMF、VMF1、GMF 3种映射函数模型基线解算NRMS值均小于0.3，表示基线解算结果都合格。对比3种模型发现，同一截止高度角下，NRMS值相差不大，随着截止高度角的增加，基线解算的NRMS值减小，说明引入了较好的观测数据。不同映射函数模型N、E、U方向基线误差结果和总体基线误差如图4所示。

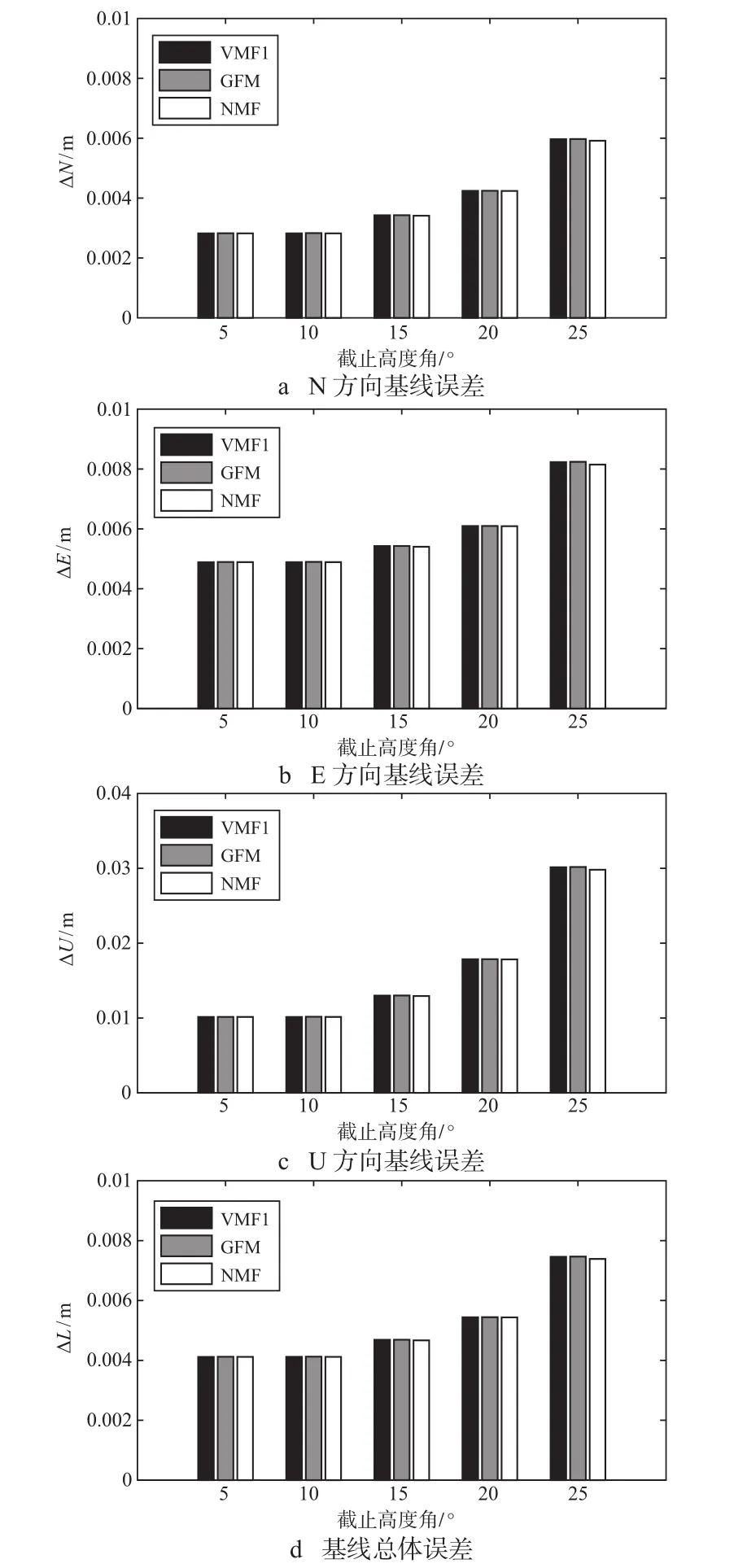
图4 不同映射函数模型N、E、U方向和总体基线误差

由图4可知，NMF、VMF1、GMF 3种映射函数模型在截止高度角5°和10°时N、E、U方向基线误差几乎没有区别， N、E方向基线误差优于5 mm，U方向基线误差优于10 mm，解算中随着截止高度角的增大，N、E、U方向基线误差逐渐增大。考虑到GNSS卫星的空间几何分布和对流层水汽的影响，在CMONOC网中的基线解算中截止高度角设置为10°时最佳。

4 结 语

本文借助CMONOC网中100个测站和2个IGS测站一个月的数据，通过对流层映射函数CMONOC网解算精度对比分析，实验结果表明：

NMF、VMF1、GMF映射函数模型在N方向上的基线误差均优于N、U方向上的基线误差，U方向上基线误差最大。在截止高度角为10°时，N、E方向基线误差优于5 mm，U方向基线误差优于10 mm。

在截止高度角为5°和10°时，3种映射函数模型对CMONOC网解算精度相当，解算中随着截止高度角的增加，3种映射函数模型在N、E、U方向上误差逐渐增大。考虑到GNSS卫星的空间几何分布和对流层水汽的影响，在CMONOC网中的基线解算中截止高度角设置为10°时最佳。

不同截止高度角情况下，3种映射函数模型对CMONOC网解算精度相当，不过考虑到VFM1映射函数模型在解算过程中需要引入模型文件，会增加解算的复杂程度，GMF映射函数模型具有全球优越性的特点，因此解算CMONOC网推荐使用GMF映射函数模型效果更佳。