基于UR3机械臂穿刺导航的末端姿态分析与运动规划

张文露 王宏 雷超 王琳琳 沙洪

中国医学科学院北京协和医学院生物医学工程研究所，天津300192

0 引 言

机器人技术不仅广泛应用于工业，而且逐步在医疗领域中崭露头角。目前，医疗机器人包括外科手术机器人、康复治疗机器人、假体和残障人士辅助机器人等[1]。其中，穿刺机器人是医疗外科机器人的分支之一，是用于微创外科手术的医疗机器人。机器人辅助穿刺手术系统主要由机械臂控制系统、成像系统、空间定位系统、工作站等组成[2]。机械臂在穿刺手术中的应用可以减少对医生经验的依赖，提高手术的精准度[3]。因为机械臂控制系统是穿刺机器人系统的重要组成部分，对其关键技术开展研究具有重要的理论与应用意义。

奇异位置是机械臂重要的运动学特性点，当处于奇异位置时，机械臂末端的运动会受到限制，导致机械臂运动失控或不能实现预定动作。为了使机械臂可以更加高效、快速地完成指定操作任务，本研究中利用D-H（Denavit-Hartenberg）法对机械臂建模，进行正、逆运动学分析和奇异位置分析，为后续的机械臂轨迹规划和控制系统设计提供理论依据。此外，设计了简易的穿刺末端执行器，编写了安装执行器后穿刺针到达目标靶点时机械臂末端位姿的计算程序及机械臂规避奇异点的程序，以实现对机械臂的自动控制，为设计机械臂辅助穿刺手术系统奠定基础。

1 仪器与方法

1.1 主要仪器

1.1.1 UR3机械臂

UR3是一种6自由度串联式机械臂，包括腰部、肩部、肘部及3个自由度的腕关节，质量为11 kg，最大负载为3 kg，工作半径为500 mm。该型机械臂的灵活性高，其各个关节都能整周回转，而且整机体积小，适合在穿刺手术场景中应用。由于UR3机械臂的机构特点满足Pieper准则[4]，其运动学逆解具有封闭解的优势，使运动控制更为容易。故本研究中，选择UR3机械臂作为研究对象进行建模。

1.1.2 末端穿刺装置

利用Solid Works软件设计了一个简易的机械臂末端穿刺套筒装置，如图1所示。该装置可直接安装到机械臂末端的法兰盘上。安装时，套筒方向与机械臂末端接口方向一致，通过控制机械臂到达穿刺位置，并且使套筒中心圆孔的方向与规划路径方向重叠，医生只需将穿刺针沿着套筒穿入体内即可。由于该套筒方向与机械臂末端的工具坐标系（tool coordinate system,TC S）的方向一致，计算时不需要重新建立坐标系，以工具坐标系中心点（tool coordinate point，TCP）为坐标原点，即可进行各关节坐标系的变换。

图1 机械臂末端穿刺套筒

1.2 机械臂运动学分析

1.2.1 机械臂建模

D-H法是一种对机械臂连杆建模及关节建模的简单方法[5-6]。D-H法不需要考虑机器人的结构顺序和复杂程度，适用于任何机器人结构。建立D-H连杆坐标系时，首先要确定各个关节的z轴，一般将每个旋转关节的轴线方向设为z轴，然后通过z轴确定x轴。x轴的确定分为三种情况，一是相邻关节的轴线既不相交也不平行，此时存在一条距离最短的公垂线，将这条公垂线定义为x轴；二是相邻关节的轴线平行，则选取与前一关节x轴平行的线作为此关节的x轴；三是相邻关节轴线相交，则定义x轴使其垂直于相邻关节轴线所在的平面。最后，在z轴和x轴都确定的条件下，通过右手定则确定y轴。通过D-H法建立UR3机械臂各关节之间的坐标系，如图2所示。坐标系{0}固连于机械臂的基座，是一个固定不动的坐标系，在研究机械臂运动学问题时可以把该坐标系作为参考坐标系。为了减小机构偏心对位姿矩阵精度的影响，将坐标系{2}移动至与坐标系{1}重合[7]。

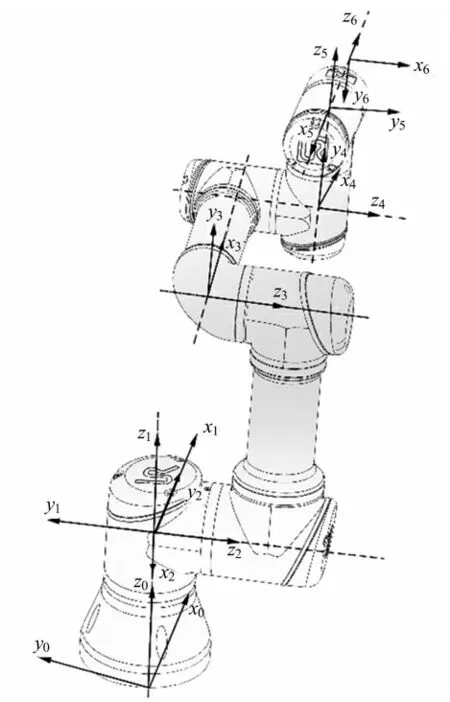
图2 UR3机械臂连杆坐标系

根据图2所示的坐标系，得到对应的D-H连杆参数，见表1。其中，关节角θi为绕zi轴，从xi-1旋转到xi的角度；连杆偏距di为沿zi轴，从xi-1移动到xi的距离；连杆长度ai为沿xi轴，从zi移动到zi+1的距离；连杆转角αi为绕xi轴，从zi旋转到zi+1的角度。根据实际需求，UR3初始位置为θ1=-pi/2，θ2=-pi/2，θ3=-pi/2，θ4=0，θ5=pi/2，θ6=0。

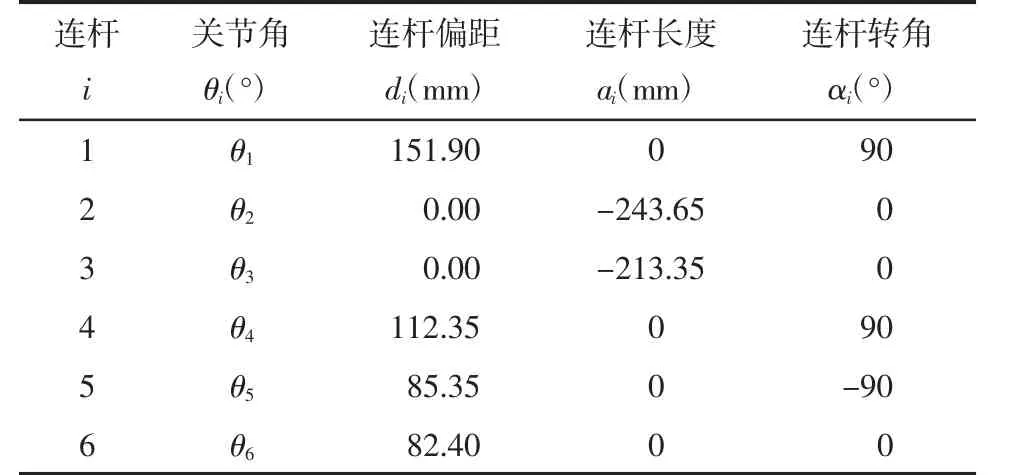
表1 UR3机械臂D-H连杆参数

1.2.2 正运动学分析

机械臂正运动学分析是已知机械臂各个关节角度值，求解出对应的机械臂末端位置和姿态[8]。由于机械臂由任意的连杆和关节以任意顺序连接而成，首先为每个关节指定一个坐标系，并求出相邻两关节的变化关系。对于UR3机械臂，先求出基座和第一个关节的变换关系，再求出第一个关节和第二个关节的变换关系，依次下去，直到求出最后一个关节的变化，把所有变换结合起来得到总变换关系，即机器人基座和末端执行器的变换关系。通过矩阵运算求导出坐标系{i-1}到坐标系{i}的变换矩阵：

化简整理得：

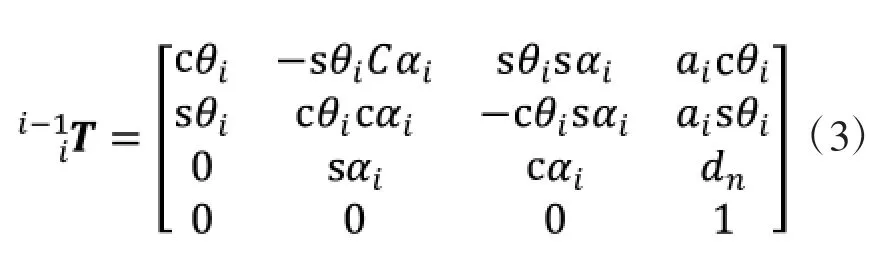
将D-H参数代入式（3）中，每个连杆的变换矩阵为：

式中：nx=s1s5c6+c1c5c6c234-c1s6s234；Ox=-s1s5s6-c1c5s6c234-c1c6s234；ax=s1c5-c1s5c234；px=d4s1+d5c1s234+d6s1c5-d6c1s5c234+a2c1c2+a3c1c23；ny=s1c5c6c234-c1s5c6-s1s6s234；Oy=-s1c6s234-s1c5s6c234+c1s5s6；ay=-c1c5-s1s5c234；py=-d4c1+d5s1s234-d6c1c5-d6s1s5c234+a2s1c2+a3s1c23；nz=s6c234+c5c6s234；Oz=c6c234-c5s6s234；az=-s5s234；pz=d1-d5c234+a2s2+a2s23-d6s5s234。

式（1）～式（5）中，px、py、pz为机械臂末端在三维笛卡尔空间坐标下的位置，即为x、y、z。sθi表示sinθi，cθi表示cosθi（i=1，2，…，6）；sθ23表示sin（θ2+θ3），cθ23表示cos（θ2+θ3），sθ234表示sin（θ2+θ3+θ4），cθ234表示co s（θ2+θ3+θ4）。

1.2.3 逆运动学分析

逆运动学的求解过程是根据机械臂末端相对于基座的坐标系（参考坐标系）的位姿，求出关节角度θ1、θ2、θ3、θ4、θ5、θ6的过程[9-10]，是机械臂运动规划和轨迹控制的基础，也是运动学中最重要的部分[11]。目前，关于机械臂逆运动学求解的方法主要有解析法[12]、几何法[13]、迭代法[14]等。本研究选择解析法进行求解[15]。

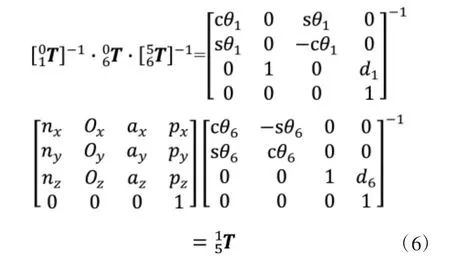
利用式（6）中左右两侧第三行第四列元素相等、第三行第三列元素相等、第三行第一列元素相等，联立方程求出θ1、θ5、θ6。

同理，

利用式（7）第一行第四列元素相等、第二行第四列元素相等，联立方程求出θ3和θ2；利用式（6）中第二行第二列元素、第一行第二列元素求解出θ2+θ3+θ4，从而求得θ4。由此，θ1～θ6均已求出。推导公式不一一列出。

UR3机械臂逆向运动学的结果一般会有多解，需要通过计算关节差的均方根（root mean square，RM S）来筛选最合适的解[16]。设当前关节角度为qs=[θs1，θs2，θs3，θs4，θs5，θs6]，目标关节角度为qe=[θe1，θe2，θe3,θe4，θe5，θe6]，则关节角度差的RMS为：

从所有的关节角度解中选取RMS值最小的，即为目标关节角度最优解q=[θ1，θ2，θ3，θ4，θ5，θ6]。

1.2.4 奇异位置分析

奇异位置是机械臂机构学中重要的特征位置，当机械臂运动到奇异位置附近时，雅克比矩阵趋于无穷大，从而需要无穷大的关节角速度和加速度，而这在现实世界中是不可能实现的。造成机械臂处于奇异位置的主要原因有两个，一是由于机械臂超出自身工作范围，机械臂末端无法到达；二是奇异位置与机械臂姿态有关，并不是一个固定的点，因此无法列出所有奇异点，但是可以将奇异点分为三类。

第一类奇异点为腕关节奇异位置，当第四轴和第六轴共线，造成系统将第四轴和第六轴瞬间旋转180°；第二类为肩关节奇异位置，当第一轴与腕关节中心点（第五轴与第六轴交点）共线时，造成系统尝试将第一轴与第四轴瞬间旋转180°；第三类为肘关节奇异位置，当腕关节中心点与第二轴、第三轴共面时，会造成肘关节卡住，无法移动。

1.3 机械臂控制程序设计

为减少医生规划次数，提高效率。本研究中，设计了一种通过沿固定轴小角度旋转提供多组位姿的方法，以规避奇异点。首先，根据规划后的穿刺点在机械臂基座标系下的末端位姿，计算出安装套筒后机械臂的末端位姿。其次，根据该位姿套筒中心的方向矢量进行小角度旋转，得到多组位姿。然后，通过UR3机械臂脚本编程，进行运动规划，排除可能由奇异点导致运动规划失败的位姿。最后，提取运动规划成功的位姿对应的运动规划关节值，并进行最优RMS值判定，选择出有最佳响应的最佳位姿。机械臂控制程序的界面如图3所示；套筒旋转示意图如图4所示；程序流程图如5所示。

图3 机械臂控制程序界面

图4 套筒旋转示意图

图5 程序流程图

2 结 果

2.1 运动学仿真验证

在MATLAB软件环境下，使用Robotics Toolbox 10.2软件对UR3机械臂进行仿真模型的创建，生成的机械臂模型如图6所示，其与实际机械臂初始位置一致。

使用基于正运动学推导过程编写的程序，随机选出6组关节角进行验证。首先，将关节角代入程序中得到x、y、z坐标的计算值；然后，将6组关节角输入到UR3机械臂的控制程序中得到x、y、z坐标的实际值；最后，将计算值与实际值进行比较。表2中的x、y、z坐标值为TCP相对于机械臂基座标系的实际位置。

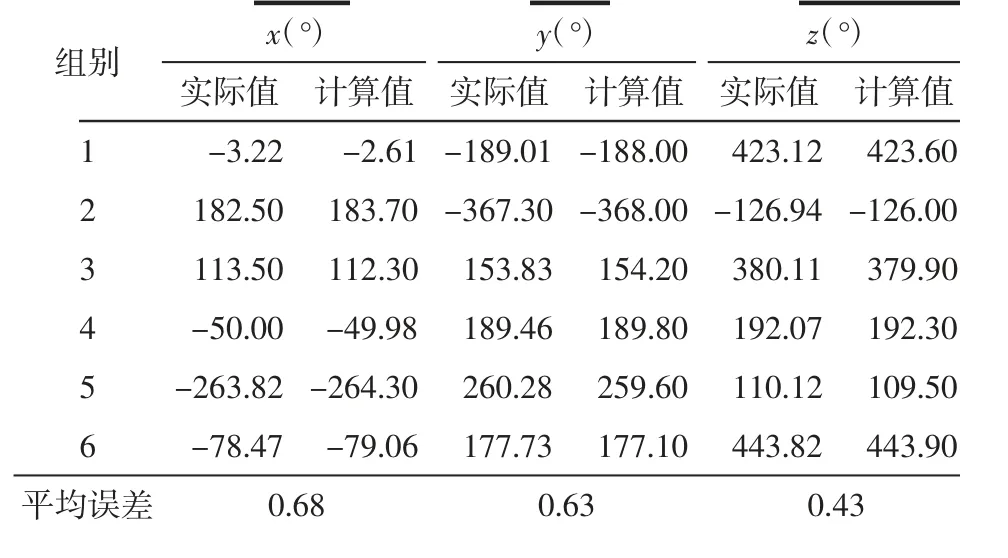
表2 计算值与实际值对比表

6组关节角度分别为：

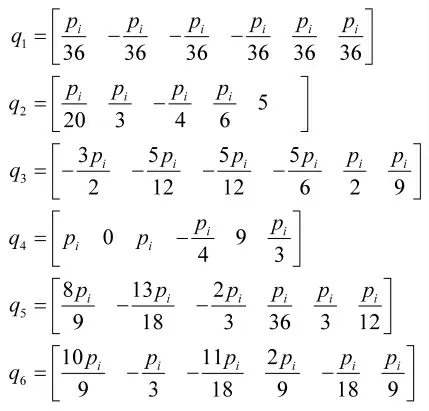
如表2所示，通过代入6组关节角度得到的x坐标的计算值与实际值的平均误差为0.68°，y坐标的平均误差为0.63°，z坐标的平均误差为0.43°。误差可能来源于连杆的长度、机械臂自身的机械误差等，故可以证明所建立的运动学模型的正确性。

2.2 运动控制程序验证

采用3D打印的模拟穿刺套筒进行实验验证。安装时，套筒方向与机械臂末端接口的方向调为一致。验证时，选择的穿刺针为9号腰椎穿刺针。考虑到实际应用中，初始位姿的规划是根据医学影像处理软件（如3D Slice等）中建立的穿刺方向，并考虑利于医师操作的基础上进行的，其结果是模拟姿态的组合。本验证实验仅验证初始规划位姿出现运动失败等情况下，规避程序的效果。在验证实验中，随机模拟3组初始规划穿刺靶点坐标及姿态（不考虑初始位姿是否为奇异点），此时得到的3组靶点位姿是基于机械臂基座标下TCP的位姿。将其输入程序中，可算出机械臂安装了套筒和穿刺针后，穿刺针针尖到达靶点时TCP的位姿。由于套筒坐标系方向和TCP方向一致，因此计算前后TCP位姿的Rx，Ry，Rz相同（Rx，Ry，Rz为机械臂末端姿态参数）。模型沿计算后的方向顺时针、逆时针各移动9次，每次移动5°，得到18组解，并通过机械臂脚本编程进行运动规划排除奇异点，剩余的解显示在界面位姿集合对话框中，并根据RMS值选出最佳位姿。

相关参数和结果见表3。其中，位置1为初始规划的TCP位姿对应的位置（x1，y1，z1），位置2为计算后，穿刺针到达靶点时TCP的位姿对应的位置（x2，y2，z2）（位置1与位置2需在机械臂工作范围内）。奇异点个数为每组位姿在进行18次旋转时对应位姿为奇异点的个数，最优RMS值为最佳位姿对应的RMS值。

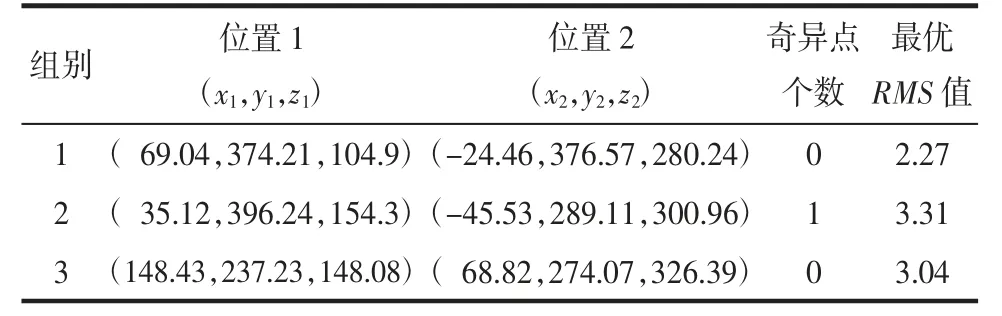
表3 相关参数和结果

将得到的最佳位姿传输到机械臂的控制系统中，以控制机械臂移动，机械臂移动完成后将穿刺针沿套筒方向穿入，针尖可到达预定目标点，如图7所示。

图7 实验结果

3 讨论与结论

本研究中，利用D-H法对机械臂进行运动学分析，并在MATLAB软件中根据推导的运动学公式编写程序进行仿真验证，为后续的机械臂轨迹规划和控制系统设计提供了理论依据。设计了简易的穿刺末端执行器，编写了穿刺针到达目标靶点时，机械臂末端位姿的计算程序。根据计算后的位姿方向，以机械臂沿其顺时针、逆时针方向各移动9次，每次移动5°的方式规避奇异点，实现了对机械臂的自动控制，为机械臂辅助穿刺手术系统的设计奠定了基础。

在实际操作过程中，也发现了一些问题。首先，计算得到的任何位姿都应该在机械臂的工作范围内，超出该范围的位姿无论机械臂怎么旋转，奇异点都无法规避。因此，对于机械臂的工作空间分析尤为必要。其次，由于对同一目标点，程序可能会得到多个位姿解，根据临床医生的反馈，并不是每种位姿都适合进行穿刺手术。虽然，本研究中基于RMS值选取了最优位姿，但不能保证其完全满足医生需求，因此在初始位姿的规划上应增加约束条件。可见，对于适用于穿刺手术的最优位姿的选取还有待进一步研究。

利益冲突所有作者均声明不存在利益冲突