基于GA-BP神经网络的电网暂稳极限切除时间预测

李昂,纪瑾,邓雅心

(1.陕西理工大学 电气工程学院,陕西 汉中 723000;2.国网青海省电力公司经济技术研究院,青海 西宁 810000)

1 引言

与社会经济迅猛发展相伴而来的是电力需求的与日俱增，电力系统安全稳定运行要求也越发严格。现阶段，进行电网安全稳定分析计算中常用的软件有PSASP、BPA等，故障极限切除时间计算是电网安全稳定计算中及其重要的一部分。文献[1-5]均利用PSASP软件进行了电网安全稳定分析，其中文献[1-3]进行了极限切除时间的计算，PSASP软件采用的计算原理为数值积分技术，里面涉及到多个高阶矩阵，但这些矩阵的组成元素并无极限切除时间这个变量，因此PSASP不能进行故障极限切除时间的自动求解，文献[1-3]均采用穷举法进行故障极限切除时间的求解。

电力系统是一个复杂且庞大的系统，穷举法的使用是费时费力的。GA-BP神经网络能够通过仿真数据对故障极限切除时间进行预测，提高电网安全稳定计算的效率。文献[6]搭建了GA-BP预测模型，通过500组变压器试验数据对变压器绕组热点温度进行预测；文献[7]通过实验得到50组柴油在不同条件下的喷雾贯穿距数据，并搭建了GA-BP神经网络预测模型对柴油喷雾贯穿距进行预测；文献[8]建立了GA-BP神经网络的果园需水量预测模型，并比较了GA-BP模型与BP模型的精度与适应度。基于以上分析，本文搭建了基于GA-BP神经网络的极限切除时间预测模型，分析了该模型对故障极限切除时间的预测能力。

2 GA-BP神经网络预测模型

2.1 BP神经网络概述

BP网络是一类多层的前馈神经网络[9]。BP算法是Rumelhart等人在1986年提出的。BP算法,其修正网络权值的方式为误差的逆向传播。BP神经网络因其结构易懂、可调参数种类多和训练算法类型多等特点,使用广泛。然而其有一些固有缺陷,如训练开销大、容易收敛至部分最优处和网络层次不易确定等。网络的计算开销与初始权值和阈值的选取关联度较大，然而无法切确获取，对于该问题常采取GA算法优化。

2.2 遗传算法优化BP神经网络

遗传算法(genetic algorithm,GA)是一种进化算法，其基本原理是效仿生物界中的“物竞天择、适者生存”的演化法则。GA将要求解的参数翻译为染色体,然后利用迭代进行染色体行为运算更改种群中染色体信息,最终留下符合优化条件的染色体。GA改进BP神经网络流程为：确定BP网络各层结构、GA寻优权值和阈值、训练BP网络进行预测。具体优化步骤如下:

Step 1：初始种群的生成。生成N个个体,单个个体为一个串结构数据,个体编码为实数编码，BP网络所有的权值和阈值均包含在单个个体中。

Step 2：确定适应度函数。单个个体的生存能力由适应度表征，下式为适应度函数F的计算方式：

(1)

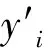
Step 3：选择。经过比较单个个体的适应度函数值Fi,用轮盘赌法选出种群中较优的个体,使其有繁殖下一代的机会。

Step 4：交叉。交叉是染色体行为中频次最高的操作。2个配对个体，nk、nm以交叉概率Px交换其部分基因，产生2个新个体，在第j位基因进行交叉产生新基因nkj、nmj。nkj、nmj的操作表达式如下：

(2)

式中：r为[0，1]间的随机数。

Step 5：变异。变异个体的选择是随机的,将选中的个体以变异概率Pm随机地使串结构数据中某个串值改变。选中个体ni在第j个基因进行变异，得到新基因nij，nij的操作表达式如下：

(3)

式中：nmax、nmin分别为基因nij的上、下界；r1为1个随机数；s为当前进化次数；smax为最大进化次数；r2为[0，1]间的随机数。

Step 6：计算新种群中个体的适应度函数值Fi，若Fi达到要求或进化次数达到最大值则进化完毕，否则返回Step 3。

Step 7：将利用GA寻优之后的权值和阈值赋予BP网络，得到极限切除时间预测模型。

3 GA-BP神经网络模型应用

3.1 极限切除时间数据采集

本文使用如图1所示的三机九节点系统作为算例。

图1 三机九节点系统单线图

系统在运行时会产生大量的数据信息，这些数据在某种程度上会反映出系统的暂态特性，为保证该预测模型的表征能力，选取输入特征量时需遵循一定的原则。首先，选取的输入特征量要具备有效性，当系统发生暂态变化时受到影响较大的物理量；其次，输入特征量要具备系统特征，不随系统的网络拓扑结构变化而失去表征能力。通过总结文献[10-12]和多次仿真验证，最终选取的输入特征量如表1所示作为网络输入，网络输出为极限切除时间。

表1 输入、输出特征量

通过PSASP软件搭建如图1所示系统图，模拟线路AC_2上不同位置处发生三相短路故障，并采集故障数据。具体数据获取操作如下：

Step 1：选取故障点。本文共选取6个故障点，此6个故障点以15%的间隔均匀的位于线路AC_2上。

Step 2：计算极限切除时间。对Step 1中所选取的故障点利用软件自身计算特点结合穷举法计算极限切除时间。

Step 3：获取故障数据。对Step 1中所选取的故障点仿真时进行输入特征量数据的采集，自故障发生时，每隔0.01s采集一次特征量数据，共采集120组数据。

3.2 极限切除时间预测结果

采用3.1所述方式共获得120组样本数据，部分测试样本数据如表2所示。

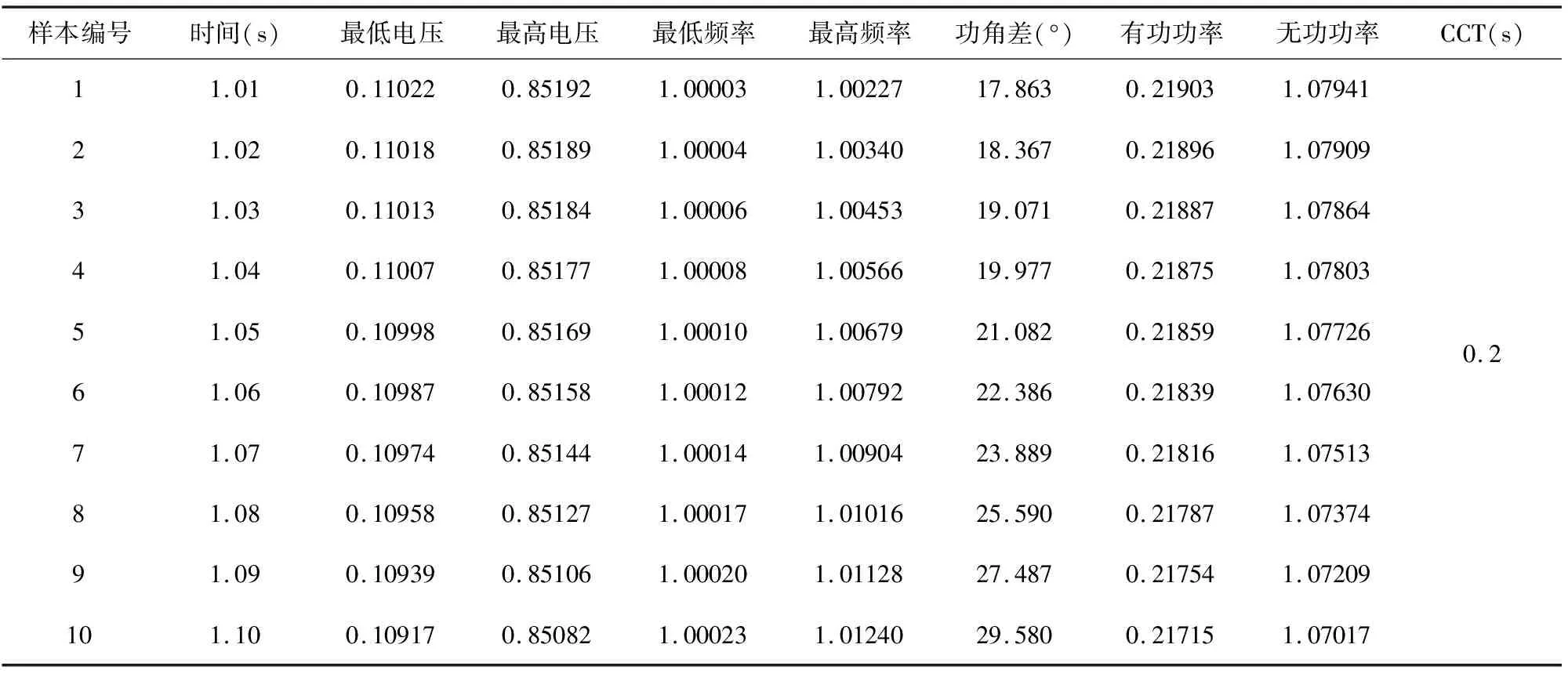
表2 部分样本数据(单位p.u.)

GA-BP模型的参数设置如下：GA的种群大小为40，交叉概率为0.6，变异概率为0.01；BP的输入层、隐含层和输出层神经元的个数分别为8，17和1，如图2所示为GA-BP模型的训练流程图。AC_2中前五组数据共100组样本作为训练集用于训练模型，AC_2中第六组数据共20组样本作为测试集用于检验模型的精度。BP输入量的量纲不唯一，故对实验所得数据进行处理，将输入量大小映射在[0,1]之间。将训练好的GA-BP模型用于预测测试集数据，测试集的预测结果如图3所示。

图2 GA-BP模型的训练流程

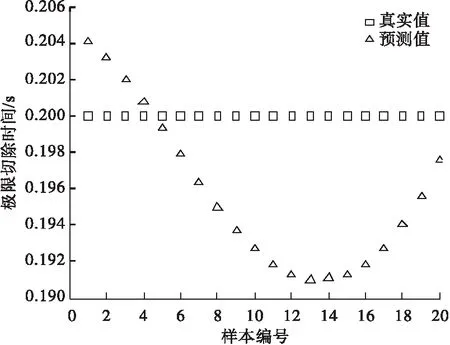
图3 测试集数据预测结果

图3中预测的数值为交流线路AC_2的90%位置处发生故障的极限切除时间，通过穷举法测得的实际值为0.200s，图2中神经网络的预测值在0.191～0.204s之间，测试集预测值的绝对误差均在±5%以内，可见GA-BP神经网络预测极限切除时间的效果较好。

为检验GA-BP预测模型的精度，采用平均相对误差(MRE)和均方根误差(RMSE)两个特征指标对基于该模型的极限切除时间预测效果进行评价，若预测效果越好则各指标值越小，计算公式如下：

(4)

(5)

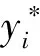
采用同样的样本数据建立BP预测模型，并利用测试集进行检验，由表3中各指标值的大小可知，GA-BP模型对极限切除时间预测效果较好。

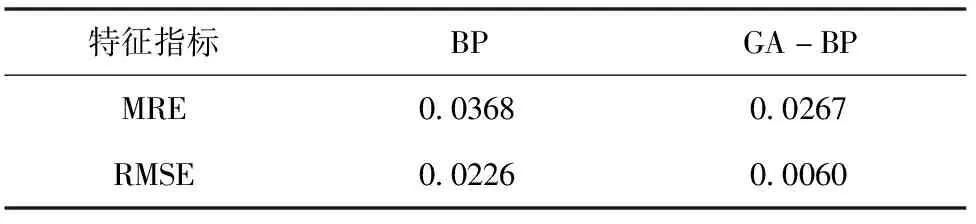
表3 预测模型的特征指标

4 结语

本文采用GA算法对BP神经网络的初始权值及阈值进行优化，并将其应用于电网暂稳极限切除时间预测领域，建立了GA-BP神经网络的极限切除时间预测模型。通过PSASP软件搭建三机九节点系统模型模拟三相短路故障并计算极限切除时间获取样本数据，利用样本数据进行模型训练及测试。结果表明，测试集数据预测值与实际值基本一致，且该模型的预测精度高于BP模型。形成了仿真软件输出数据，GA-BP模型调用仿真数据，准确计算极限切除时间的良性循环，提高了电网安全稳定计算的效率。