大口径快速反射镜的模糊自适应PID控制

蔡玉生，朱 军，石 磊，张景忠

〈系统与设计〉

大口径快速反射镜的模糊自适应PID控制

蔡玉生1,2，朱 军3，石 磊1，张景忠4

（1. 中国科学院长春光学精密机械与物理研究所，吉林 长春 130033；2. 中国科学院大学，北京 100049；3. 山东核电有限公司，山东 烟台 265116；4. 黑龙江省森林保护研究所，黑龙江 哈尔滨 150000）

快速反射镜能否精确稳定跟踪目标取决于良好的伺服控制性能。快速反射镜的通光口径越大，柔性支撑铰链和驱动器设计难度就越大，同时也会对伺服控制提出更高的要求。针对此问题，本文提出模糊自适应整定PID（proportional integral derivative）控制算法，该算法既能运用模糊推理进行自适应整定控制参数，又能继承传统PID控制器便于工程实现。本文对音圈电机（voice coil motor）驱动的500mm大口径快速反射镜进行控制器设计且进行仿真实验，并将其结果与基于传统PID控制下的相比较。结果表明，基于模糊自适应整定PID控制的500mm大口径快速反射镜的超调量为5.40%，调节时间51.0ms，且抗干扰能力强于传统PID控制。此外，与传统PID控制相比，本文提出的控制方法提高了500mm大口径快速反射镜的响应速度，减小了跟踪误差，提升了500mm大口径快速反射镜系统的跟踪性能和鲁棒性。

快速反射镜；大口径；音圈电机；模糊控制；自适应整定PID

0 引言

快速反射镜由精密伺服控制相应的转角从而精确控制光束的偏转角度，它相对于普通的反射镜具有响应速度快、工作带宽高、指向精度高等优点[1-2]。伴随着航空光学成像、遥感技术等领域对成像分辨率的要求不断提高，大口径、长焦距光学系统在光电稳定平台获得广泛的应用。为满足大口径航空光学系统成像的高质量的要求，基于大口径快速反射镜温度-高度环境下的高精度跟瞄测试方法，大口径快速反射镜模拟框架粗稳伺服残差，测试光学系统精稳跟踪性能，能较真实地评估光学系统成像质量。如图1所示。

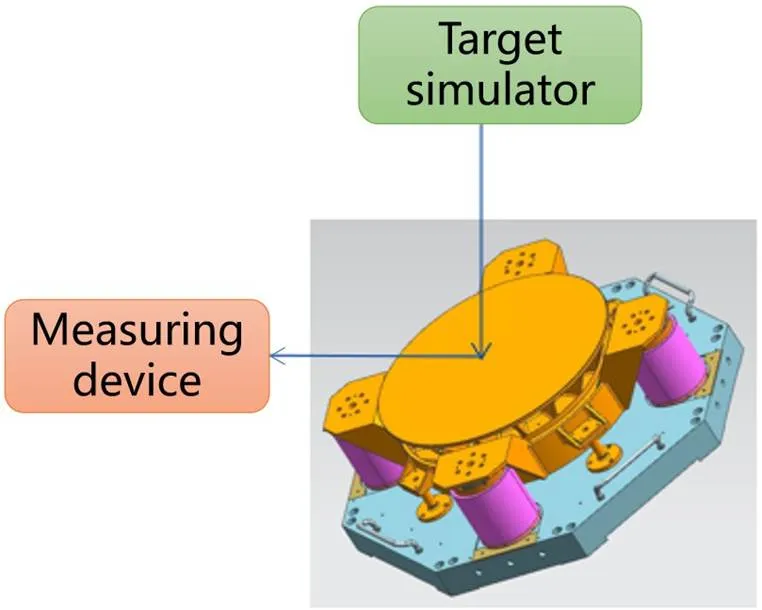
图1 模拟应用简图

其中对于大口径快速反射镜的控制方法决定了其稳定性能，间接地影响对光学系统成像质量的评价。其中文献[3]采用改进根轨迹方法去设计PID（proportional integral derivative）参量，保证良好的系统动态性能且改善系统机械谐振问题。但该方法需精准系统模型数学表达式。文献[4]采用改进自抗扰的方法，验证了低频信号下，该方法在原有自抗扰算法的基础上减小系统响应时间，提升系统跟踪精度。但缺乏工程化的理论保障。文献[5]采用基于内积的逆模型补偿方法可获得较好的控制效果，但当外界环境变化或受到干扰，则需要重新设计。

因此本文提出模糊自适应整定PID控制算法，在传统PID控制算法基础上，引入模糊理论和参数自整定方法，既具有模糊理论不完全依赖于精确模型，又能发挥出传统PID控制设计上简单、易于工程实现、鲁棒性好等特点。

1 f500mm大口径快速反射镜系统的结构与模型

1.1 大口径快速反射镜系统简介

本文以500mm大口径快速反射镜系统为研究对象，由反射镜、音圈电机、控制器、线性功率放大器、电涡流位移传感器、反射镜基座等部分组成。该系统机械结构如图2所示。

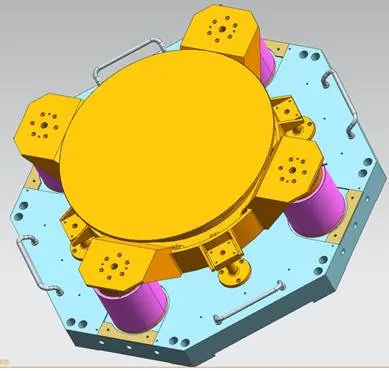
图2 f500mm大口径快速反射镜结构

该反射镜系统有、两轴，每一个轴上装有两个音圈电机，反射镜安装在镜托上，镜托又通过“金字塔”状柔性铰链[6]（如图3所示）与反射镜基座相连，同一轴上两个音圈电机直线运动推挽镜托，围绕旋转中心形成推挽力矩，推动“金字塔”状柔性铰链产生弹性位移，进而使得反射镜偏转。反馈测量元件为电涡流传感器，安装位置是与两轴成45°夹角。

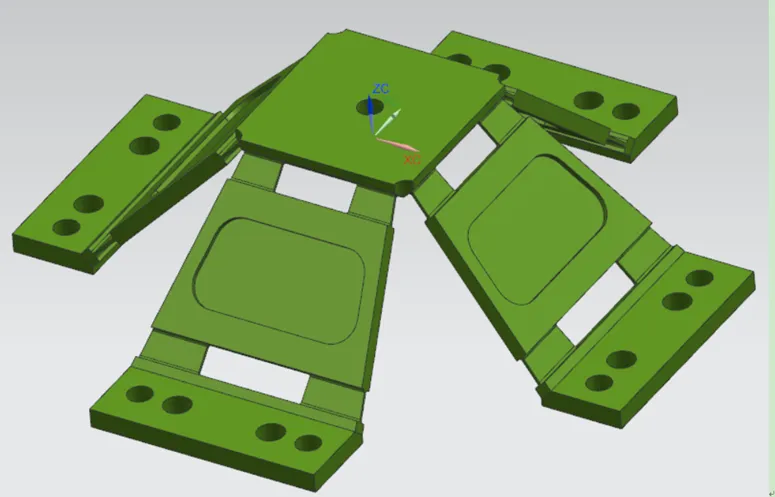
图3 “金字塔”状柔性铰链

其工作原理为当给定输入信号时，控制器根据相应控制算法将控制量输出到音圈电机驱动器上，同轴上的两个音圈电机获得大小相等且方向相反的驱动力，进而产生推挽驱动力矩，推动“金字塔”状柔性铰链在这个轴线方向上产生位移变化，通过电涡流传感器检测位移的变化（转换为转角），反馈给控制器，形成一个闭环控制系统。500mm大口径快速反射镜的控制框图如图4所示。

图4 f500mm FSM系统控制原理框图

1.2 大口径快速反射镜系统的数学模型

500mm大口径快速反射镜系统中包含有功率放大器、电涡流传感器、“金字塔”状柔性铰链和音圈电机等部分。其中功率放大器，传感器、柔性铰链等数学模型都可等效为一个比例模块，主要是音圈电机的数学模型的建立，将其等效为一个质量-阻尼-弹簧模型。如图5所示。其中力学平衡方程方程为：

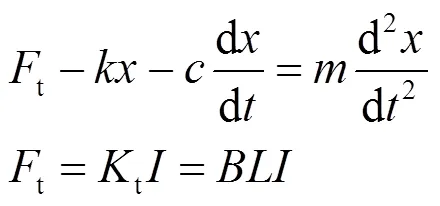
电压平衡方程为：

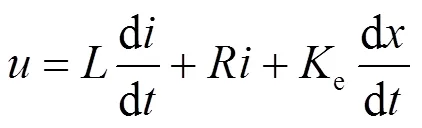
式中：为作用在质量块上的力；为阻尼系数；为电流；为弹簧弹性系数；为位移；为电机电感；为电机内阻；t为推力常数；e为反电动势系数。

图5 质量-阻尼-弹簧模型

根据各部分元器件的物理特性，建立大口径快速反射镜系统的数学模型如图6所示。

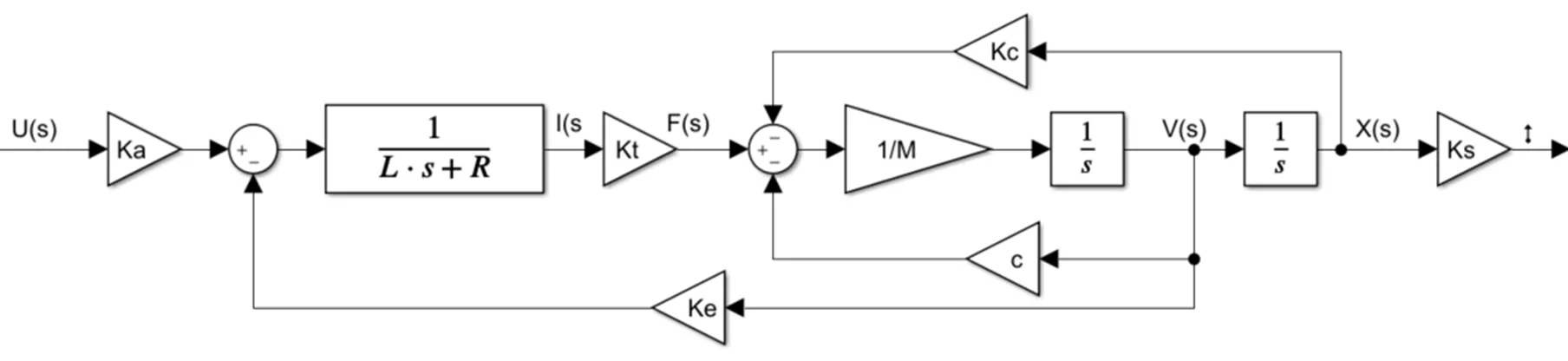
图6 系统数学模型

各参数的定义如表1所示。

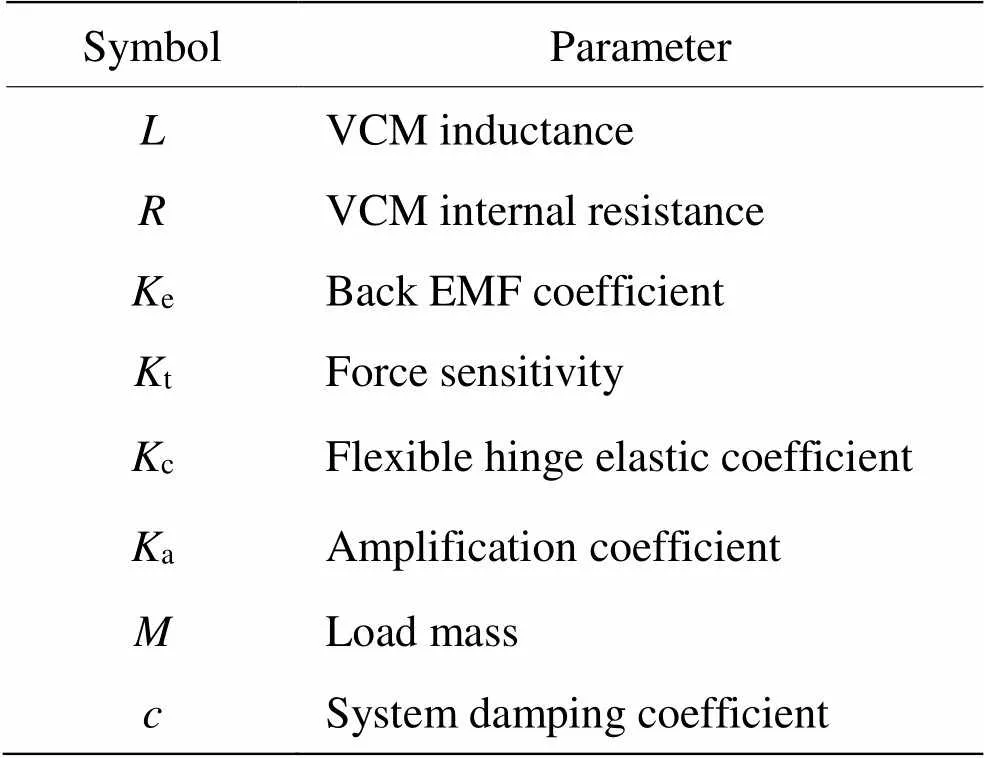
表1 数学模型的参数定义

根据图6可以求得被控对象的传递函数为：

式中：为复频率。

但由于实际系统中，音圈电机的电感数值非常小，可以忽略不计。

本文采用白噪声为输入信号，偏转位移角度作为输出信号，采用Matlab中的系统辨识工具箱对大口径快速反射镜系统进行模型辨识，得到500mm大口径快速反射镜系统的开环传递函数为：

式(4)就作为下面实验部分的被控对象的数学模型，对它展开实验仿真。

2 模糊自适应整定PID控制

2.1 模糊理论

模糊理论可解决专家经验不易精确描述和不易定量表示等问题。其运用模糊数学理论和方法，用模糊数集表示规则的条件、操作，并把控制规则以及其他有关信息（如初始PID参数、评价指标等）作为知识库存入到计算机中，然后根据实际系统的响应情况，运用模糊理论推理，得到最佳输出参数，即可实现对最佳PID参数的自动调整[7]。

模糊控制器是把误差和误差变化率c作为输入，以满足任意时刻的和c对PID调节器中p、i、d3个参数自整定的要求[8]，其控制器结构如图7所示。

2.2 模糊控制

模糊控制的核心就是模糊控制器，具备下列3个功能：

①将系统偏差从准确数字量转化为模糊量，即为模糊化过程。

②由给定的对应模糊规则对模糊量进行模糊推理。

③将推理后的模糊输出量转化为精确量，即为反模糊化。

2.2.1 模糊化

模糊化是对精准数字量到模糊量的转换。模糊化过程中的模糊化函数一般用隶属度函数来表示。图8有常用的3种模糊化函数。

设输入变量为、c，输出变量为p、i、d，且定义模糊变量对应的变化区间[－6,6]，对应论域为：

、c、p、i、d＝{－6,－4,－2,0,2,4,6}

并设其模糊子集为：

、c、p、i、d＝{NB,NM,NS,Z,PS,PM,PB}

其中N、Z、P表示负、零、正。B、M、S表示大、中、小。输入、输出变量的隶属度曲线如图9、图10所示。

2.2.2 建立模糊控制规则表

知识库包含规则库和数据库。通常以规则表的形式表示模糊规则。

根据3个控制参数p、i、d在控制过程中的作用及其变化对控制系统产生不同的影响，得到模糊控制器中3个控制参数的自整定原则。

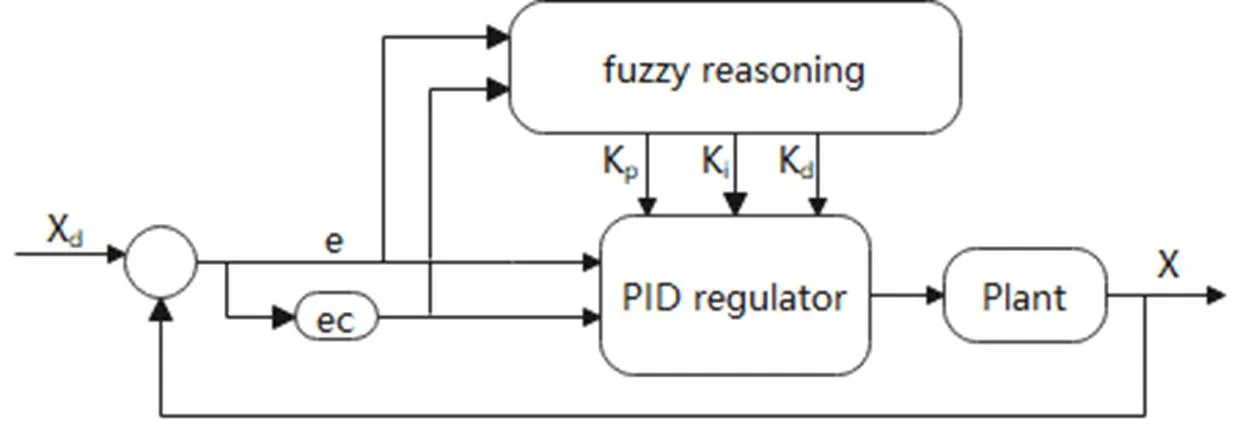
图7 模糊控制器结构图

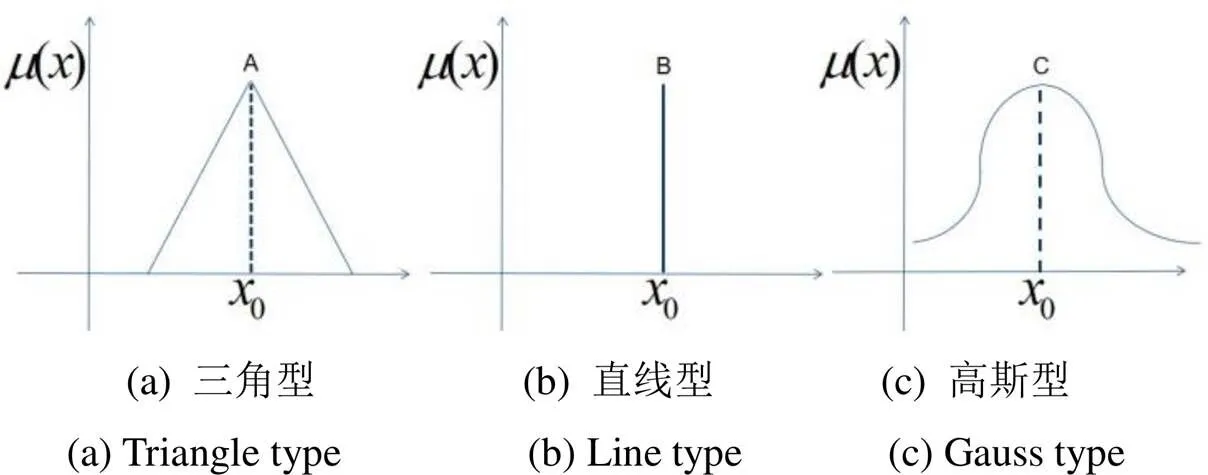
图8 三种模糊化函数

图9 e、ec的隶属度曲线

图10 Kp、Ki、Kd的隶属度曲线

参考文献[9]中自整定原则并综合专家的控制经验，建立如下模糊逻辑语句。

1) If (is NB) and (cis NB) then (pis PB)(iis NB)(dis PS)

2) If (is NB) and (cis NM) then (pis PB)(iis NB)(dis NS)

3) If (is NB) and (cis NS) then (pis PM)(iis NM)(dis NB)

......

49) If (is PB) and (cis PB) then (pis NB)(iis PB)(dis PB)

由以上逻辑模糊语句可以得到以下p、i、d的模糊规则表（如表2～表4所示）。

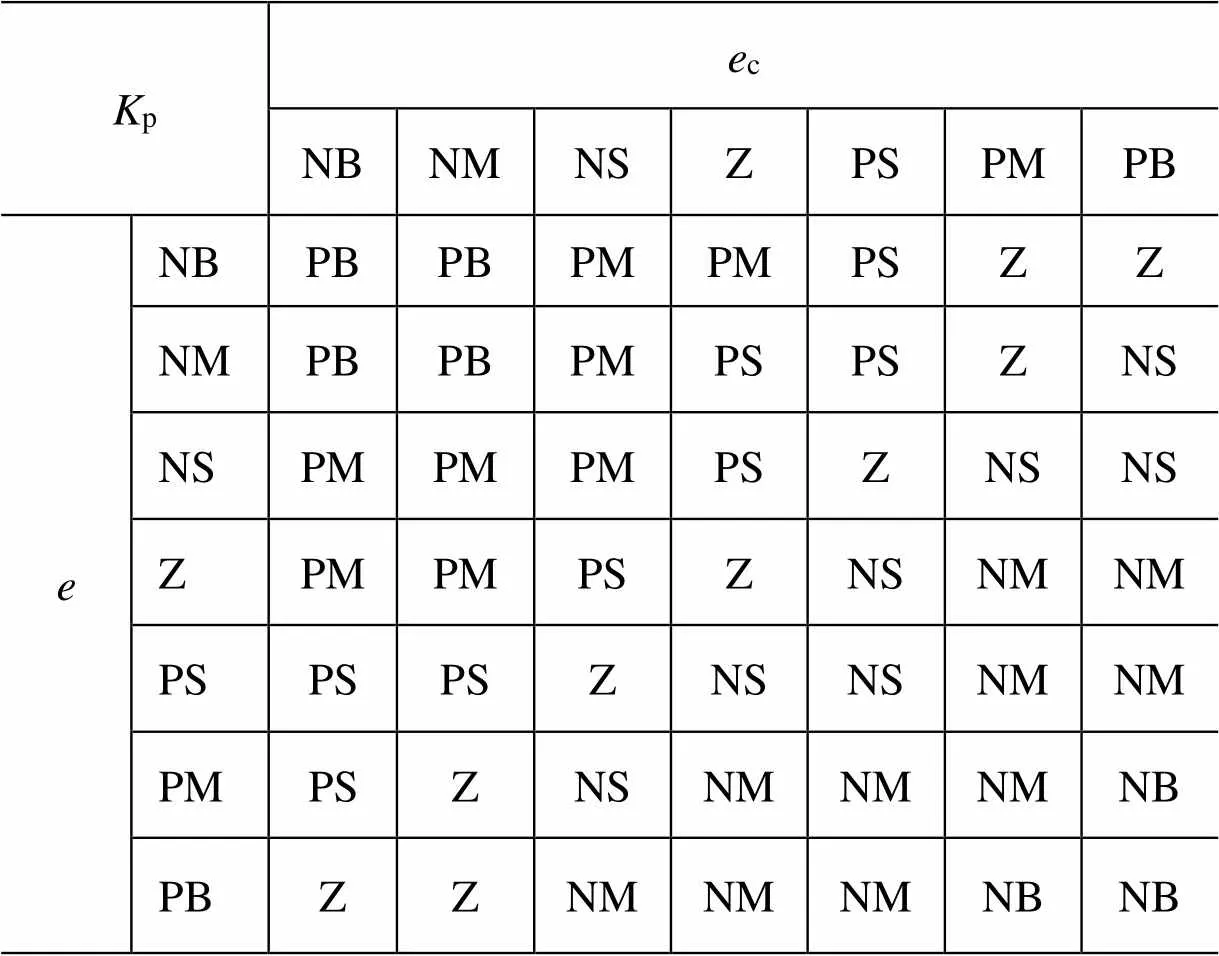
表2 Kp的模糊规则表

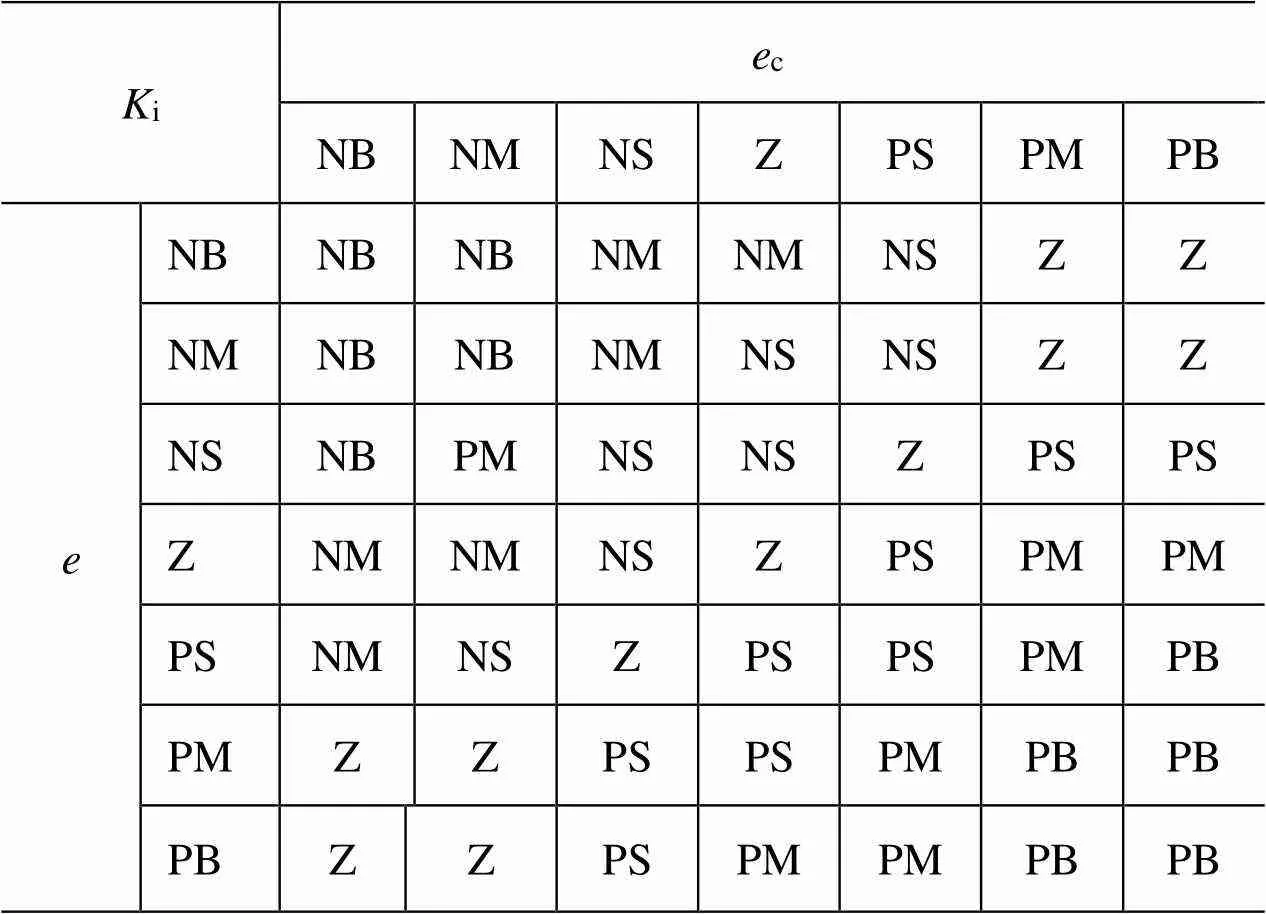
表3 Ki 的模糊规则表

2.2.3 反模糊化处理

反模糊化过程就是精确化。在模糊集合中取出代表模糊推理结果最大可能性的精确值。

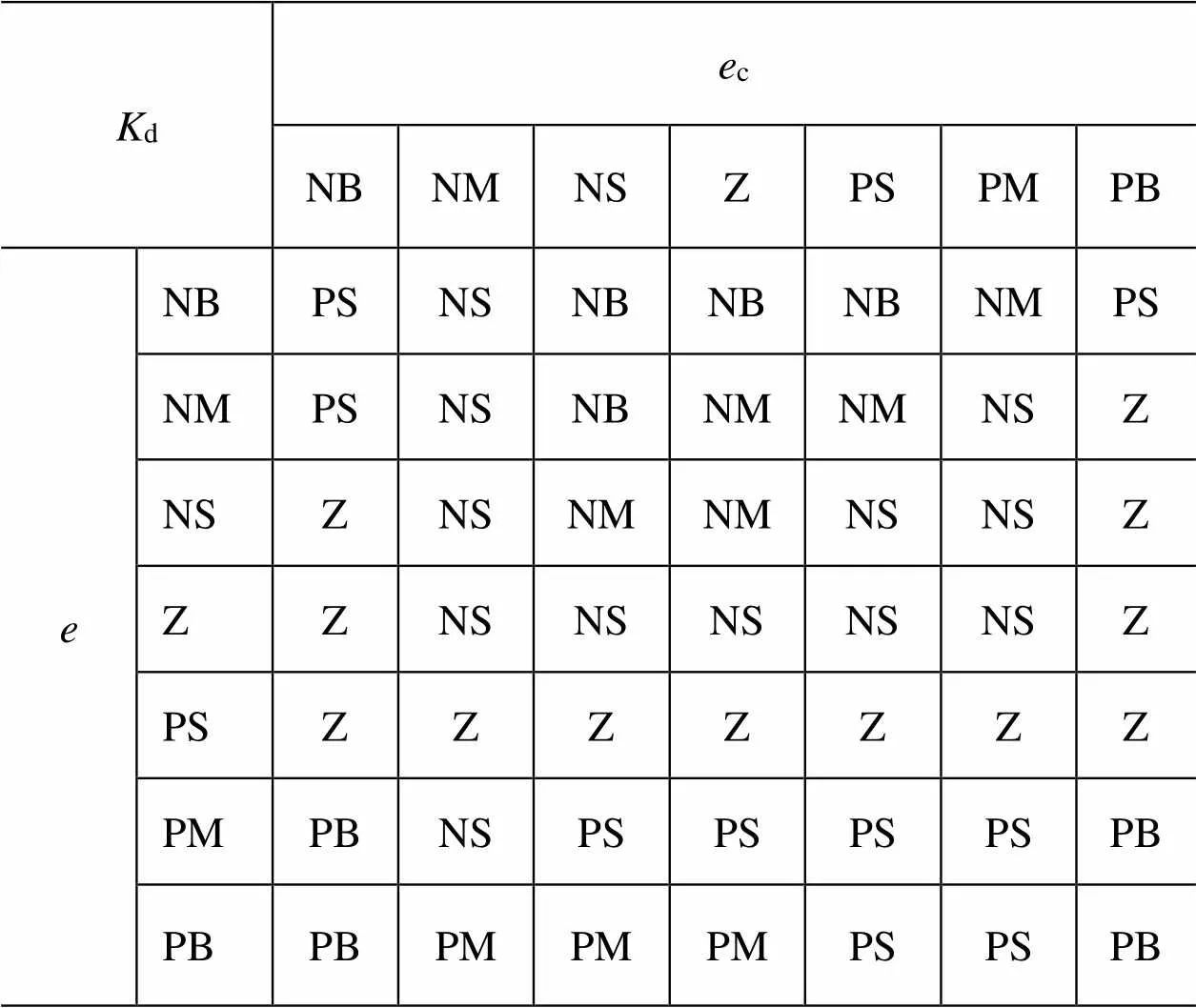
表4 Kd的模糊规则表

综合考虑，最大隶属度函数法常用于对控制要求不高且计算相对简单的系统，而重心法的推理控制输出会更加平滑，因此本文采用重心法来进行反模糊化处理。得到p¢、i¢、d¢的模糊控制调整参数，定义参数p、i、d调整算式如下：

3 系统仿真分析

在Matlab/Simulink中搭建整个系统模型如图11所示，基于模糊控制与基于传统PID控制的500mm大口径快速反射镜仿真模型。

传统的PID控制参数通过临界比例度法[11]整定控制参数，得到的3个参数p、i、d，同时显示阶跃输入信号（在某一时刻加干扰）、正弦信号，传统PID输出和模糊自适应PID输出如图12、图13所示，500mm大口径快速反射镜系统的阶跃响应如图14所示，正弦信号跟踪如图15所示。

根据上图12、图13、图14、图15输出波形可分析得到，模糊自适应PID与传统PID控制相比，动态性能上调节时间更短，超调量也稍小，能够比较迅速地进入稳态，并且抗干扰的能力更强，能较快恢复到系统的稳定状态。具体数值如表5所示。

图11 f500mm FSM系统模型

图12 控制系统阶跃响应输出

Fig.12 Control system step response output

图13 控制系统正弦跟踪输出

Fig.13 Control system sine tracking output

图14 f500mm快速反射镜系统阶跃响应

Fig.14 f500mm FSM system step response

图15 f500mm快速反射镜系统正弦跟踪

Fig.15 f500mm FSM system sine tracking

表5 控制性能对比

针对模糊控制部分，进一步观察模糊控制器的3个输出p、i、的变化如图16、图17所示。

由图16、17分析可见，模糊控制器的3个输出参数随着系统调节发生变化，待系统趋于稳定后，参数不再发生变化且趋于稳定。对于正弦响应，系统稳态一直在变化，3个参数输出也一直处于类似正弦规律性变化。

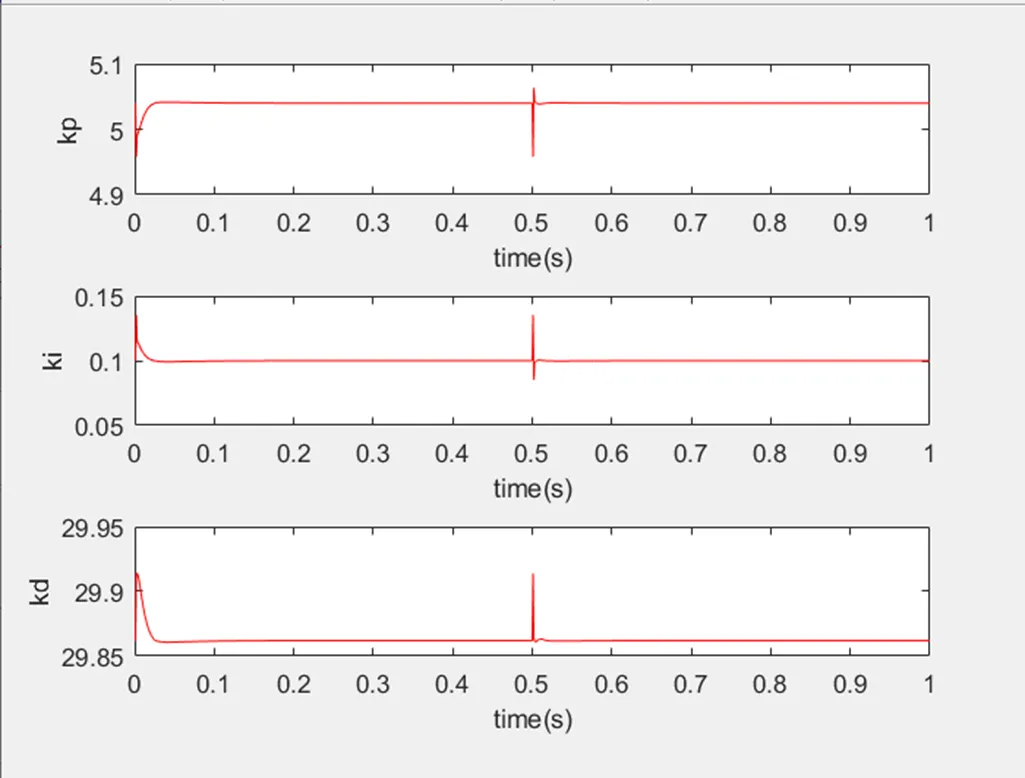
图16 阶跃信号下Kp、Ki、Kd的变化曲线

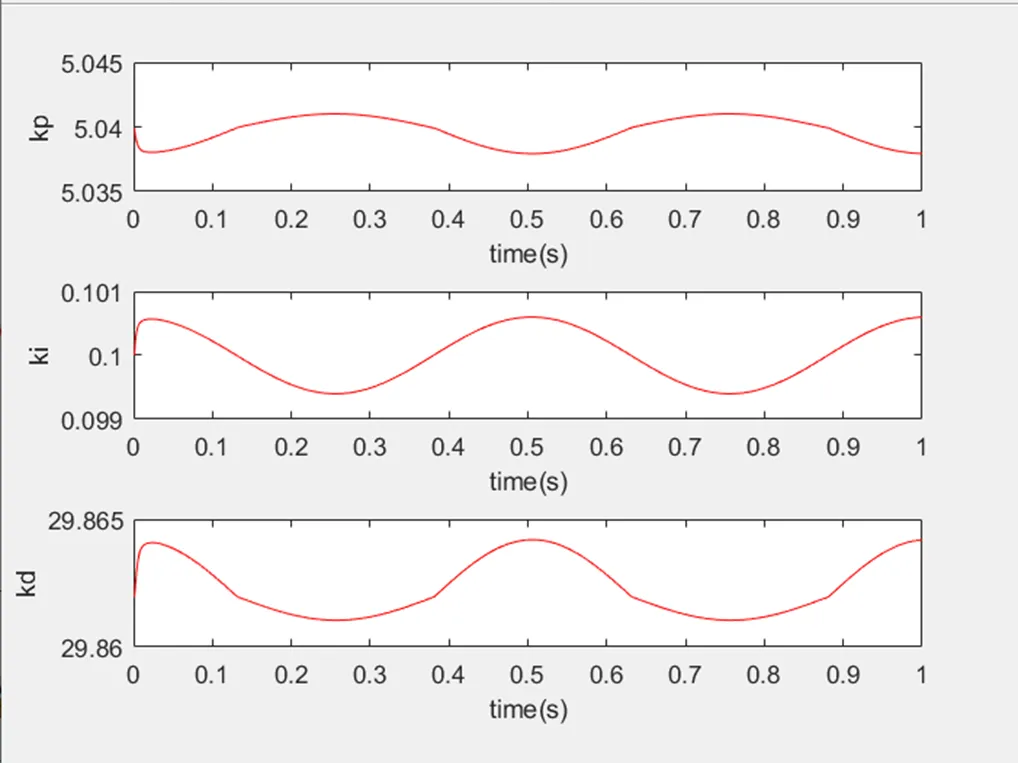
图17 正弦信号下Kp、Ki、Kd的变化曲线

4 结论

与传统PID控制相比，本文提出的控制算法，系统上升时间缩短至12.8ms左右，超调量减小了31%左右，达5.4%，调节时间提前2.2倍左右，达51ms左右，而且抗干扰能力相对较强。均优于传统PID控制，明显改善大口径快速反射镜系统的动态、稳态性能，提高了响应速度，减小了跟踪误差。所以选用大口径快速反射镜去模拟框架的粗稳伺服残差进而检测光学成像系统的精稳跟踪性能。航空光学成像检测系统的精度能直接评价成像质量好坏。系统检测精度越高，就能对光学成像质量给出越高的评价，具有重大意义。

模糊控制算法的控制效果很大程度上依赖于专家控制经验，因此整个系统的动态、稳态性能受到专家控制经验的局限，但人工智能和机器学习的不断发展[12]，上述存在问题慢慢就会有新的解决途径。

[1] KLUK D J, BOULET M T, TRUMPER D L. A high-bandwidth, high-precision, two-axis steering mirror with moving iron actuator[J]., 2012, 22(3): 257-270.

[2] 刘力双, 夏润秋, 吕勇, 等. 音圈电机快速控制反射镜研究现状[J]. 激光杂志, 2020, 9(1): 1-7.

LIU Lishuang, XIA Runqiu, LV Yong, et al. Research situation of fast steering mirror driven by voice coil motor[J].,2020, 9(1): 1-7.

[3] 艾志伟, 谭毅, 吴琼雁, 等. 改进根轨迹的快速反射镜控制参量设计[J]. 激光技术, 2017, 41(4): 558-561.

AI Zhiwei, TAN Yi, WU Yanqiong, et al. Design of control parameters for fast steering mirrors by improving root locus[J]., 2017, 41(4): 558-561.

[4] 魏文军, 赵雪童. 基于改进自抗扰的快速反射镜控制研究[J]. 红外技术, 2018, 40(11): 1071-1076.

WEI Wenjun, ZHAO Xuetong. Fast steering mirror control based on improved active disturbance rejection[J]., 2018, 40(11): 1071-1076.

[5] 党选举. 压电陶瓷执行器的神经网络实时自适应逆控制[J]. 光学精密工程, 2008, 20(7): 1266-1272.

DANG Xuanju. Real-time adaptive inverse control based on neural networks for piezo ceramic actuator[J]., 2008, 20(7): 1266-1272.

[6] 石磊, 许永森, 沈宏海, 等. 一种大口径偏摆镜[P]. 中国: CN 107526159B [2019-09-10].

SHI Lei, XU Yongsen, SHEN Honghai, et al. A large-aperture deflection mirror[P]. CHINA : CN107526159B[2019-09-10].

[7] 欧长劲, 吴海列, 李军, 等. 基于模糊神经网络的SBR污水处理控制系统研究[J]. 计算机测量与控制, 2006, 14(12): 1643-1645.

OU Changjin, WU Hailie, LI Jun, et al. Study of SBR control system based on fuzzy neural network[J]., 2006, 14(12): 1643-1645.

[8] 陈泰潮. 基于模糊自适应PI控制的电梯调速系统仿真研究[J]. 机电技术, 2018,3(1): 135-137.

CHEN Taichao. Simulation research on elevator speed regulation system based on fuzzy adaptive PI control[J]., 2018: 3(1): 135-137.

[9] 赵继庭, 金刚石, 高旭辉. 基于快速反射镜的模糊自适应PID控制算法研究[J]. 激光与红外, 2018, 48(6): 756-761.

ZHAO Jiting, JIN Gangshi, GAO Xuhui. Fuzzy adaptive PID control algorithm based on fast steering mirror[J]., 2018, 48(6): 756-761.

[10] Bullard A, Shawki I. Responder fast steering mirror[J].- The International Society for Optical Engineering, 2013, 6(2): 88-91.

[11] 于明星, 王瑛, 邵帅, 等. 基于Matlab的临界比例度法在工程PID参数自整定数值模拟中的应用[J]. 辽宁师专学报: 自然科学版, 2018, 2(1): 6-8.

YU Mingxing, WANG Ying, SHAO Shuai, et al. Application of critical proportioning method based on Matlab in PID parameters auto-tuning numerical simulation in engineering[J]., 2018, 2(1): 6-8.

[12] 孟子流, 李腾龙. 机器学习技术发展的综述与展望[J]. 集成电路应用, 2020, 37(10): 56-57.

MENG Ziliu, LI Tenglong. Review and prospect of machine learning technology[J]., 2020, 37(10): 56-57.

Fuzzy Adaptive PID Control of Large Aperture Fast Steering Mirror

CAI Yusheng1,2，ZHU Jun3，SHI Lei1，ZHANG Jingzhong4

(1.,,,130033,;2.,100049,; 3.,265116,; 4.,150040,)

The ability of a fast-steering mirror (FSM) to track a target accurately and steadily depends on its servo control performance. The larger the aperture of the FSM is, the more difficult it is to design the flexible supporting hinge and the driver; in addition, it will also demand greater requirements on the servo control. To solve this problem, this paper proposes a fuzzy adaptive tune(FAT) proportional integral derivative (PID) control algorithm, which not only uses fuzzy theory for adaptively tuning the control parameters, but also inherits the classic PID controller for engineering realization. In this study, we designed a controller for the500mm FSM driven by a voice coil motor, conducted simulation experiments, and compared the results with the simulation results based on classic PID control. According to the results, the overshoot was 5.4%, the settling time was 51.0ms based on FAT PID control, and the capacity of resisting disturbance was stronger than that of the classical PID control. In addition, compared with traditional PID control, the proposed control method improved the500mm FSM response speed, decreased the tracking error, and improved500mm FSM system tracking performance and robustness.

fast steering mirror, large aperture, voice coil motor, fuzzy control, adaptive tuning PID

TP273

A

1001-8891(2021)06-0523-09

2020-12-24；

2020-12-30.

蔡玉生（1994-），男，湖北黄冈人，硕士研究生，主要从事精密机械控制研究。E-mail：caiys1994@163.com。

黑龙江省省属科研项目（CZKYF2020B0009）。