层次分析法在粮食烘干设备评价体系中的应用*
王佩琦 夏朝勇 高 兰
(郑州中粮科研设计院有限公司 450000)
在对粮食烘干设备进行综合评价时,很难找到一种适合的方法对其进行综合定量评价,本文将层次分析法巧妙地运用到粮食烘干设备的综合评价体系当中,通过此种方法能够将多个定性的指标量化[1],将计算出各个指标的层次单排序及总排序结果作为参考依据,从而定量地评定出设备的优劣好坏[2],为粮食烘干、粮食输送清理等相关设备的综合评价提供一种解决方法。
1 层次分析法简介
层次分析法(The Analytic Hierarchy Process,简称AHP)是美国运筹学家匹茨堡大学教授Saaty T L于20世纪70年代初提出的一种层次权重决策分析方法[3]。层次分析法是指将一个复杂的多指标决策问题作为一个系统,将目标分解为多个指标或准则,进而分解为多指标(或准则、约束)的若干层次,通过定性指标模糊量化方法算出层次单排序(权数)和总排序,以作为目标(多指标)、多方案优化决策的系统方法[8]。
层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构,然后用求解判断矩阵特征向量(即权重)的办法,求得每一层次的各元素对上一层次某元素的优先权重,最后再加权和的方法递阶归并各备择方案对总目标的最终权重,此最终权重最大者即为最优方案。采用层次分析法的分析流程图如图1所示[9-10]。
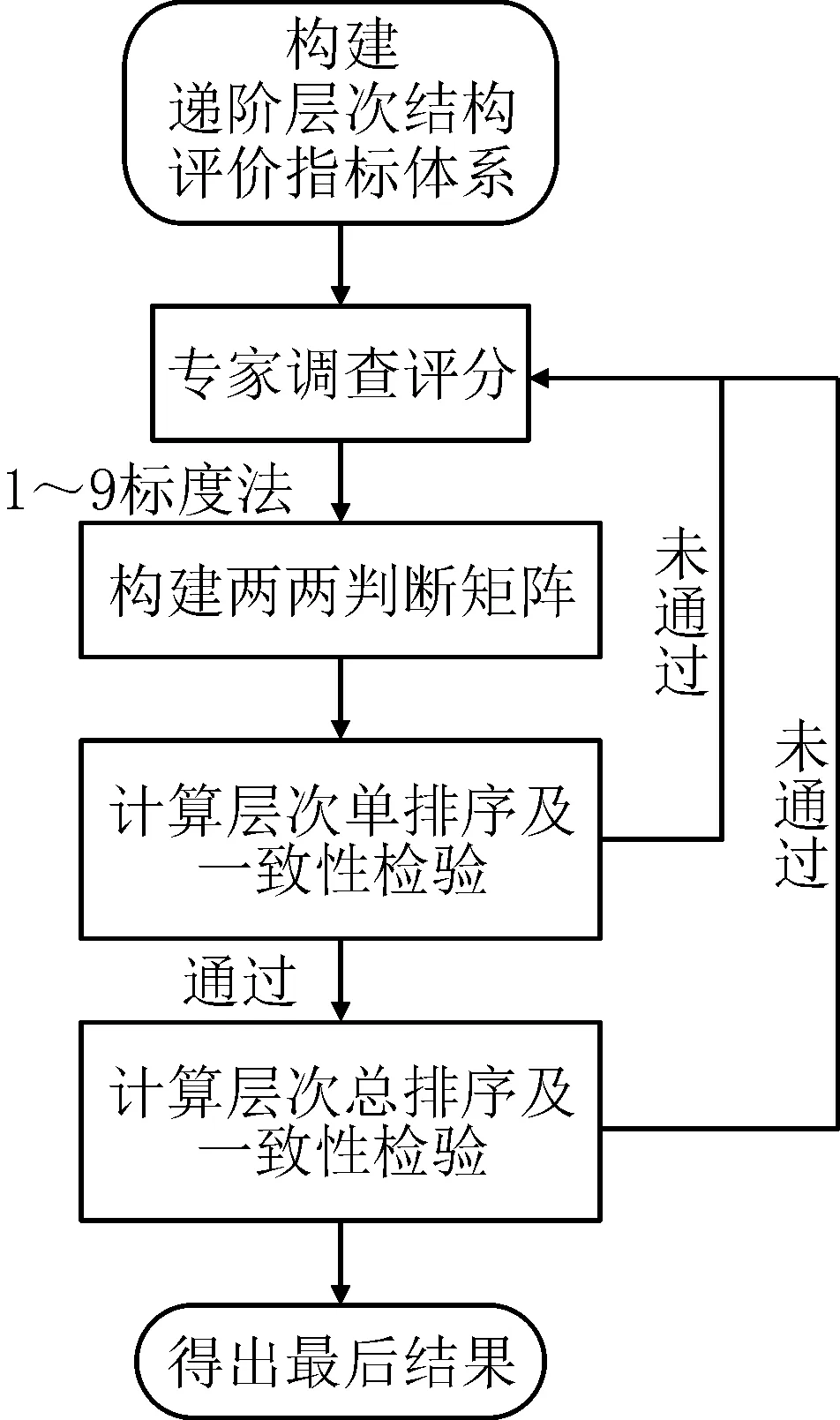
图1 层次分析法的分析流程图
2 利用层次分析法对粮食烘干设备进行综合评价
本文以连续式粮食烘干设备为例,其他类型的粮食烘干设备综合评价可参照此例,以此类推。
2.1 建立递阶层次结构评价指标体系
要解决的问题是对连续式粮食烘干设备进行综合性能评价,因此设目标层A为连续式粮食烘干设备综合评价,为实现这一综合评价目标,考虑从以下5项主要指标进行评价,即:设备性能指标、质量指标、设备质量指标、环保指标、其他指标。
通过深入调研,对此5项主要指标进行细化,细化出更为具体全面的19项评价指标,分别为:降水幅度、干燥处理量、干燥成本、单位热耗、热效率、粮食水分不均匀度、破碎率增值、裂纹率增值、出机粮温、烘干后粮食外观质量、漆膜厚度、漆膜附着力、焊接质量、粉尘浓度、噪声、(热源废气排放也是一项重要评价指标)、电气设备功能、可清理性、排量机构流量调节范围、模拟显示屏功能。从相互关系上分析,这些因素不属于主要指标,因此放在下一层次考虑,并且分属于不同准则层。因此,设5项主要指标为准则层B,19项细化指标为准则层C,措施层为连续式干燥机1(D1),连续式干燥机2(D2),连续式干燥机……
这样构成的递阶层次结构综合评价指标体系图如图2所示。
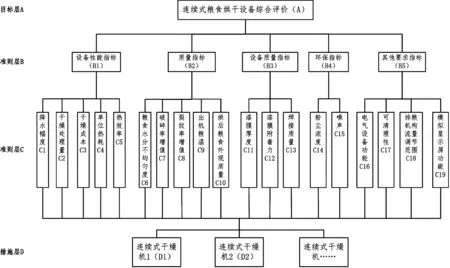
图2 连续式粮食烘干设备综合评价递阶层次结构指标体系图
2.2 构造判断矩阵并赋值
根据递阶层次结构图就能很容易地构造判断矩阵。
构造判断矩阵的方法是:每一个具有向下隶属关系的元素(被称作准则)作为判断矩阵的第一个元素(位于左上角),隶属于它的各个元素依次排列在其后的第一行和第一列[12-13]。
本研究填写判断矩阵采取的方法为:邀请专门从事粮食烘干领域研究的专家,对连续式粮食烘干设备的评价指标体系中每一层次各指标的相对重要性进行两两比较,并按其重要性程度评定等级,其中两个元素两两比较哪个重要,重要多少,对重要性程度按1~9赋值,得到判断矩阵[7]。其中,重要性标度值如表1所示[5]。

表1 重要性标度值
征求专家意见,填写后的判断矩阵如表2~表4所示。
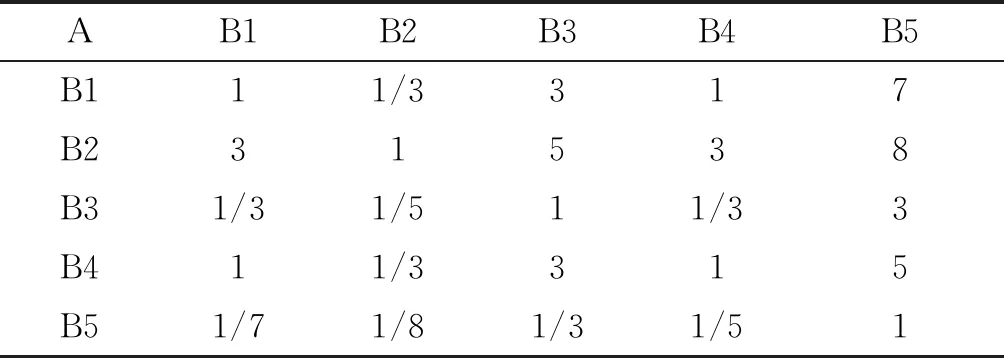
表2 准则层B的判断矩阵
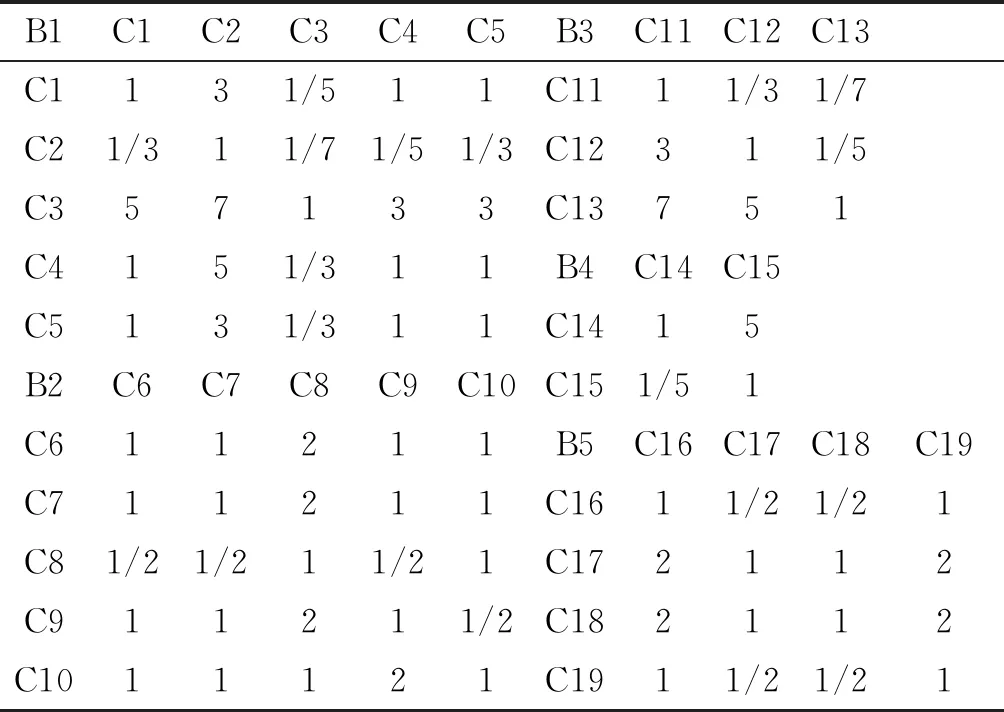
表3 准则层C的判断矩阵
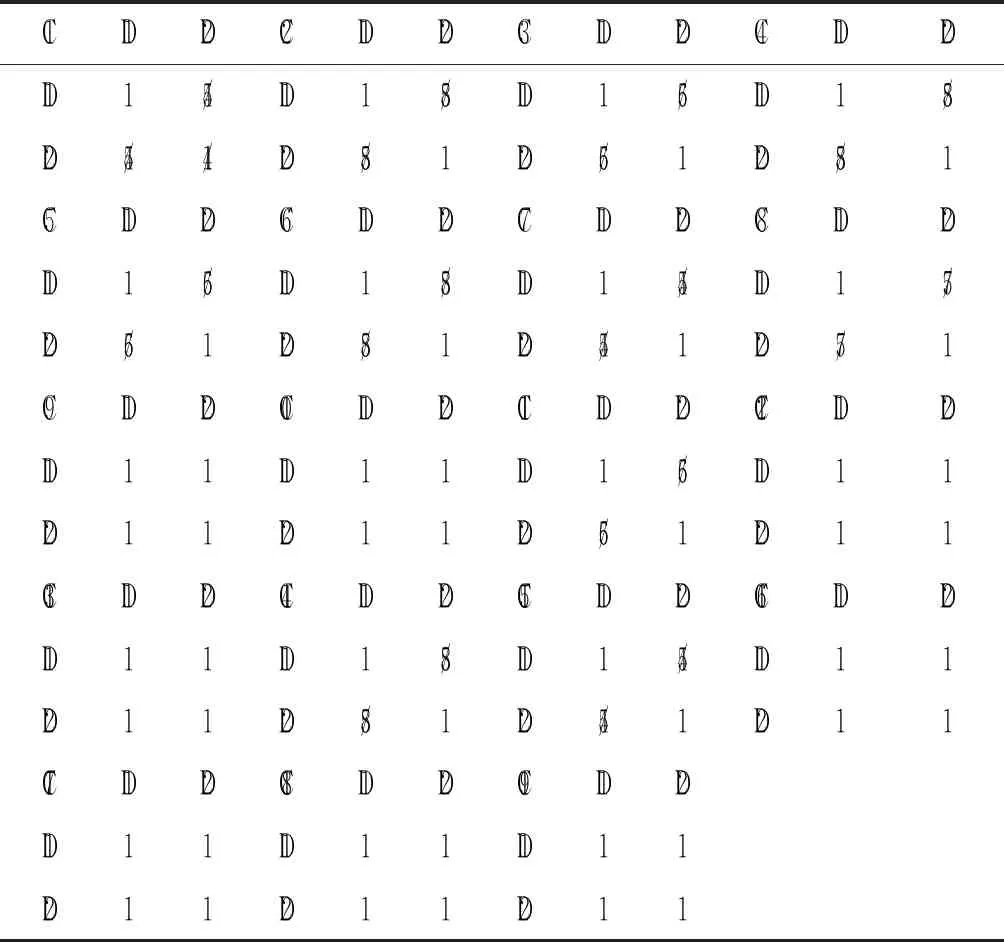
表4 措施层D的判断矩阵
本例中,措施层D2代表某个待进行综合性能评价的连续式干燥机,D1代表综合性能处于平均水平的连续式干燥机。
2.3 层次单排序(计算权向量)及一致性检验
对于专家填写后的判断矩阵,利用一定数学方法进行层次排序。
层次单排序是指每一个判断矩阵各因素针对其准则的相对权重,所以本质上是计算权向量。计算权向量有特征根法、和法、根法、幂法等,可根据判断矩阵的具体情况采用适合的算法进行计算,本文采用根法进行计算。
计算步骤:①计算判断矩阵A的每一行元素乘积
②计算Mi的n次方根
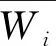
④计算最大特征值
式中,(AW)i表示向量AW的第i个分量。
在层层排序中,要对判断矩阵进行一致性检验。一个正确的判断矩阵重要性排序是有一定逻辑规律的,例如若A比B重要,B又比C重要,则从逻辑上讲,A应该比C明显重要,若两两比较时出现A比C重要的结果,则该判断矩阵违反了一致性准则,在逻辑上是不合理的。
因此在实际中要求判断矩阵满足大体上的一致性,需进行一致性检验。只有通过检验,才能说明判断矩阵在逻辑上是合理的,才能继续对结果进行分析。一致性检验的步骤如下。
表5 平均随机一致性指标RI标准值
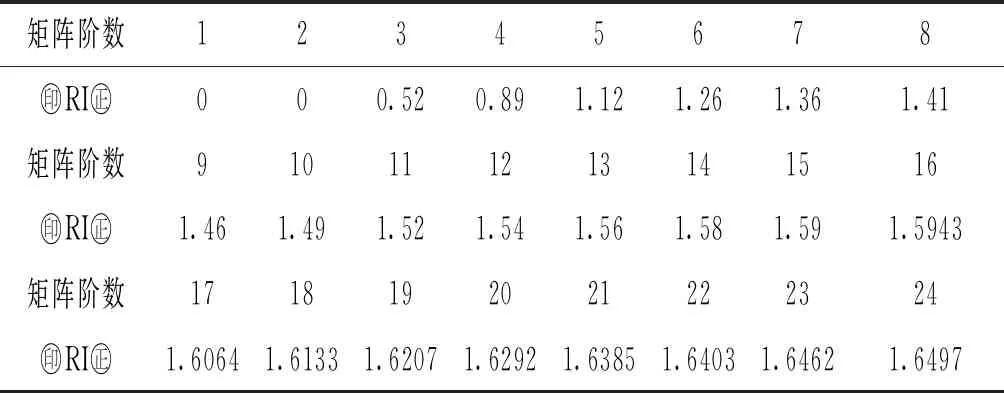
表5 平均随机一致性指标RI标准值
矩阵阶数12345678㊞RI㊣000.520.891.121.261.361.41矩阵阶数910111213141516㊞RI㊣1.461.491.521.541.561.581.591.5943矩阵阶数1718192021222324㊞RI㊣1.60641.61331.62071.62921.63851.64031.64621.6497
注:标准不同,RI值也会有微小的差异。
考虑到一致性的偏离可能是由于随机原因造成的,因此在检验判断矩阵是否具有满意的一致性时,还需将CI和随机一致性指标RI进行比较,得出检验系数CR,公式如下:
①准则层B对目标层A的比较矩阵A

根据根法计算步骤,计算判断矩阵A的权重:
权重WA≈(0.213,0.467,0.084,0.199,0.037),
判断矩阵A的最大特征根λmax(A)=5.122,一致性检验指标
CIA=0.0305,因为n=5,所以查表得RIA=1.12,随机一致性比率通过一致性检验,接受比较矩阵的判断及求得的权重系数。

综上所述,计算所得的权向量及一致性检验结果见下表6所示[4]。
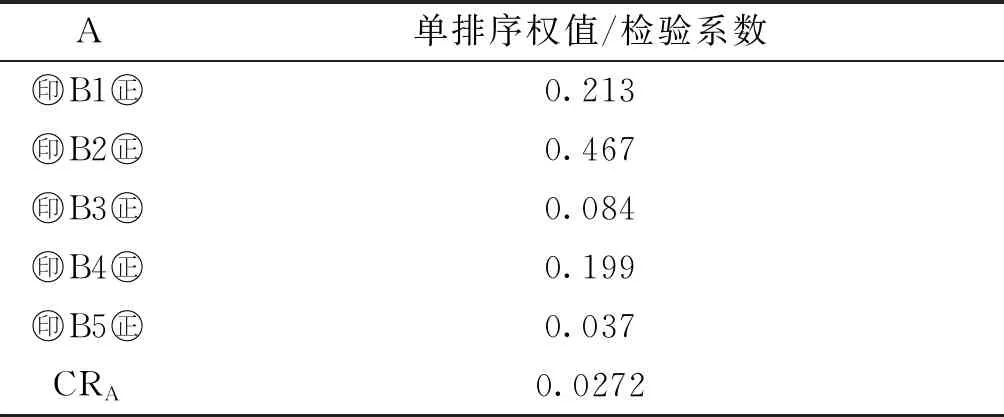
表6 连续式粮食烘干设备的权向量及一致性检验计算结果表
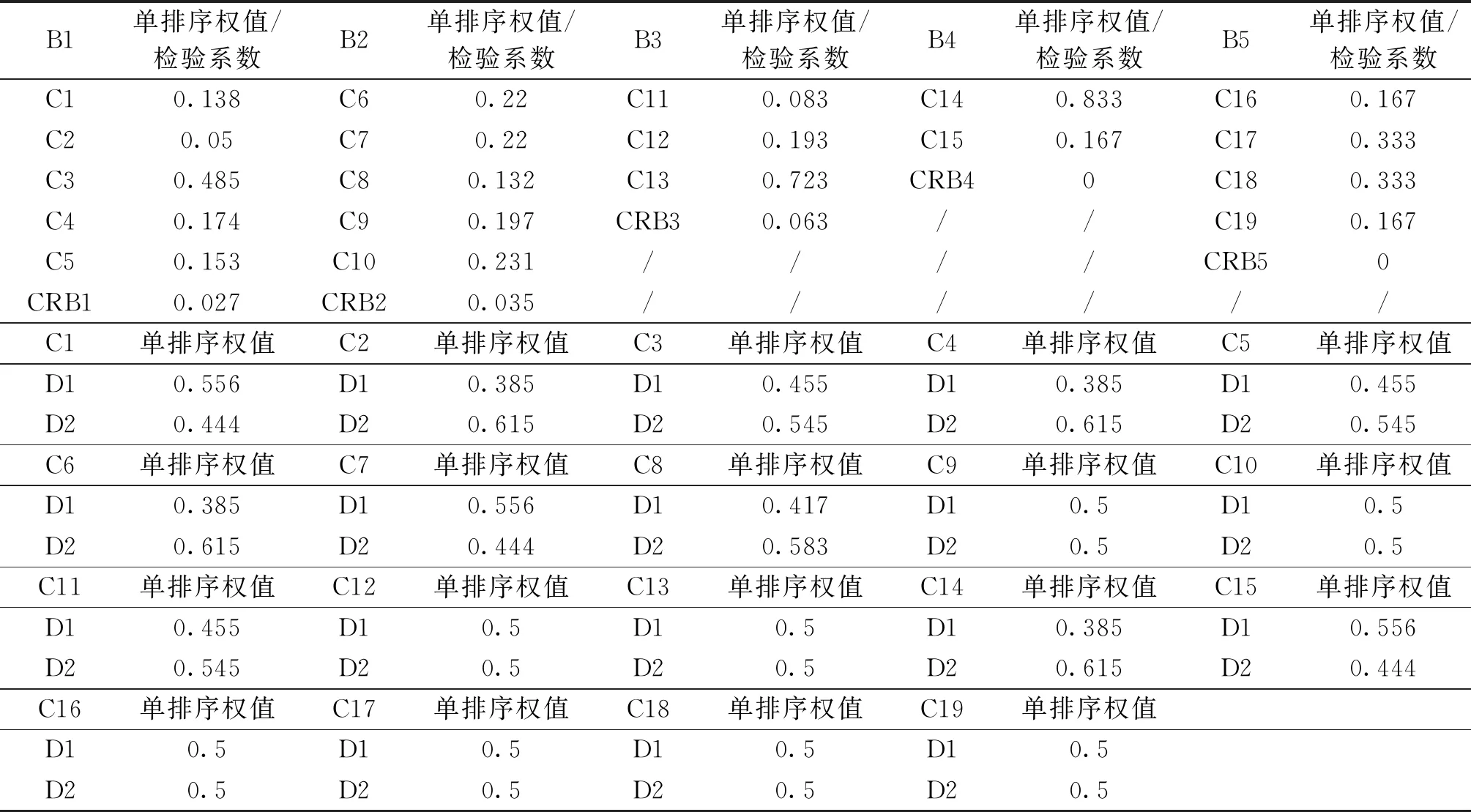
(续表6)
通过定量计算,准则层B层的5项主要指标在连续式粮食烘干设备综合评价中的层次单排序权值(权重)如图3所示[6]。
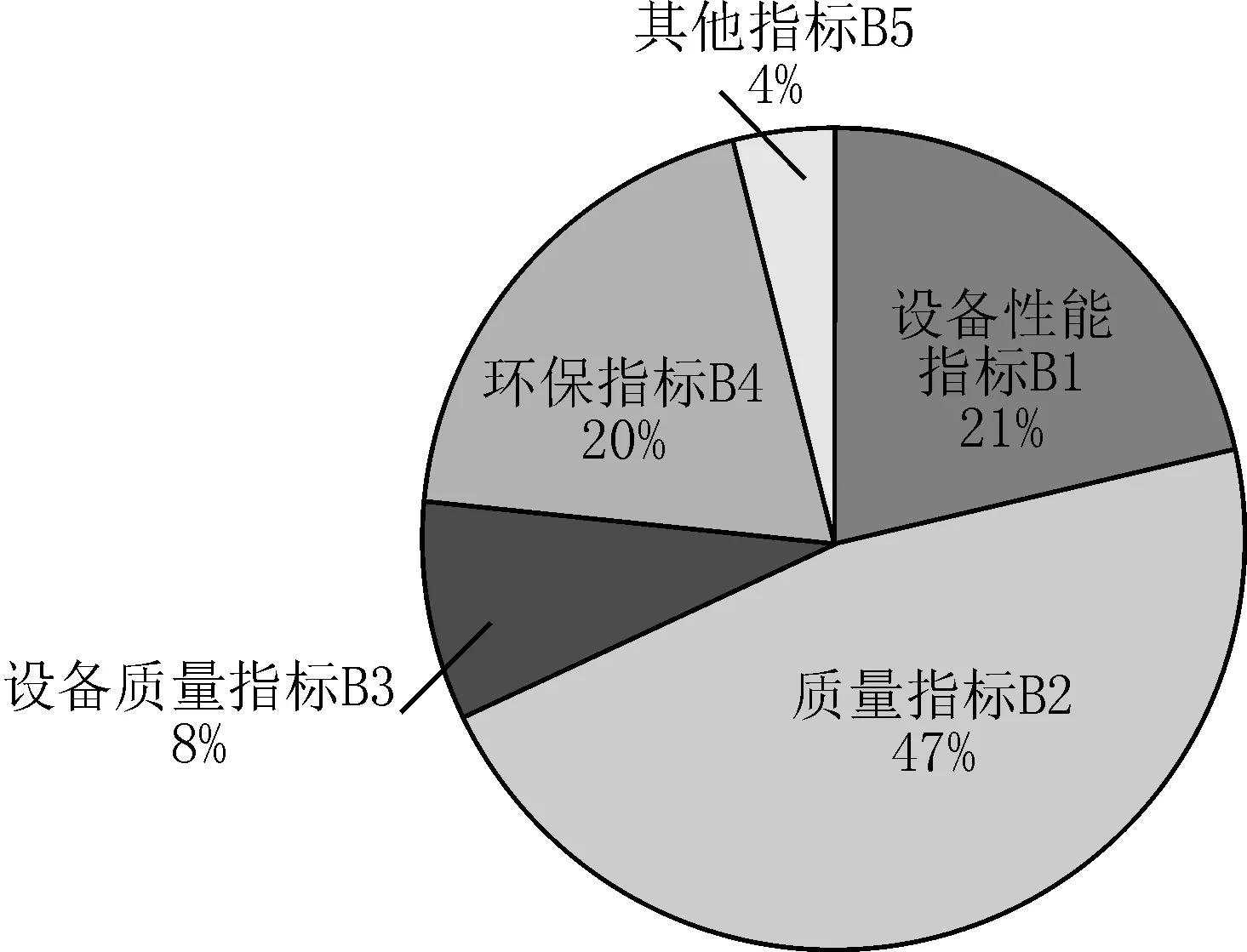
图3 准则层B层的五项主要指标层次单排序权值
2.4 层次总排序计算及一致性检验
总排序是指每一个判断矩阵各因素针对目标层(最上层)的相对权重。这一权重的计算采用从上而下的方法,逐层合成。
很明显,第二层的单排序结果就是总排序结果。假定已经算出第k-1层m个元素相对于总目标的权重w(k-1)=(w1(k-1),w2(k-1),…,wm(k-1))T,第k-1层n个元素对于上一层(第k层)第j个元素的单排序权重是pj(k)=(p1j(k),p2j(k),…,pnj(k))T,其中不受j支配的元素的权重为零。令P(k)=(p1(k),p2(k),…,,pn(k)),表示第k层元素对第k-1层个元素的排序,则第k层元素对于总目标的总排序为:
w(k)=(w1(k),w2(k),…,wn(k))T=p(k)w(k-1)
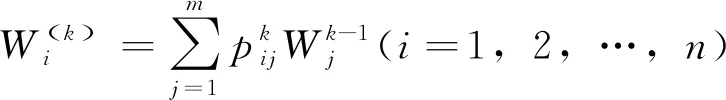
同样,也需要对总排序结果进行一致性检验。
假定已经算出针对第k-1层第j个元素为准则的C.I.j(k)、R.I.j(k)和C.R.j(k),j=1,2,…,m,则第k层的综合检验指标
C.I.j(k)=(C.I.1(k),C.I.2(k),…,C.I.m(k))w(k-1)
R.I.j(k)=(R.I.1(k),R.I.2(k),…,R.I.m(k))w(k-1)
当C.R.(k)<0.1时,认为判断矩阵的整体一致性是可以接受的。
根据上述公式计算准则层C层指标C1的总排序值WC1:
WC1=PC1WB1=0.138×0.213=0.0293
其中,PC1为指标C1的单排序值,WB1为指标B1的总排序值,由于指标B1位于第二层,第二层的单排序结果就是总排序结果,指标C1的单排序值及指标B1的总排序值计算结果见表6可查。
同理,可计算准则层指标C层指标C2的总排序值WC2:
WC2=PC2WB1=0.05×0.213=0.0107
其中,PC2为指标C2的单排序值。
计算准则层C层指标C6的总排序值WC6:
WC6=PC6WB2=0.22×0.467=0.103
其中,PC6为指标C6的单排序值,WB2为指标B2的总排序值。
计算措施层D层D1的总排序值WD1:
WD1=PD1C1WC1+PD1C2WC2+…+PD1C19WC19=0.556×0.029+0.385×0.011+…+0.5×0.007≈0.46
其中,PD1C1为D1相对于C1的单排序值,PD1C2为D1相对于C2的单排序值,……PD1C19为D1相对于C19的单排序值,WC1指标C1的总排序值,WC2指标C2的总排序值,……WC19指标C19的总排序值。
同理,可计算其他指标的总排序值,计算过程此处不再赘述,经计算,层次总排序计算结果如表7所示[11]。
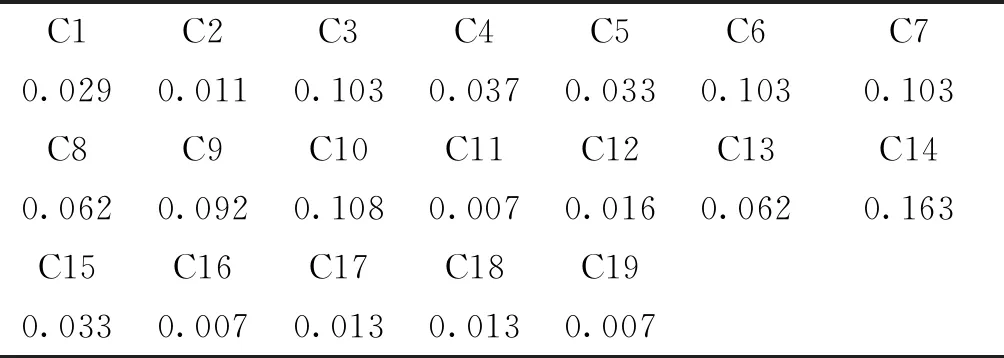
表7 连续式粮食烘干设备层次总排序结果汇总表

D1D20.460.54
对总排序结果进行一致性检验:
经计算CIC1=CIC2=…CIC19=0,其中CIC1为准则层C层C1的一致性指标,……CIC19为准则层C层C19的一致性指标,CID=CIC1WC1+CIC2WC2+…+CIC19W19=0×0.029+0×0.011+…+0×0.007=0,CRD=0<0.1,通过一致性检验。
通过定量计算,准则层C层的19项细分指标在连续式粮食烘干设备综合评价中的层次总排序权值(权重)分布见图4所示。
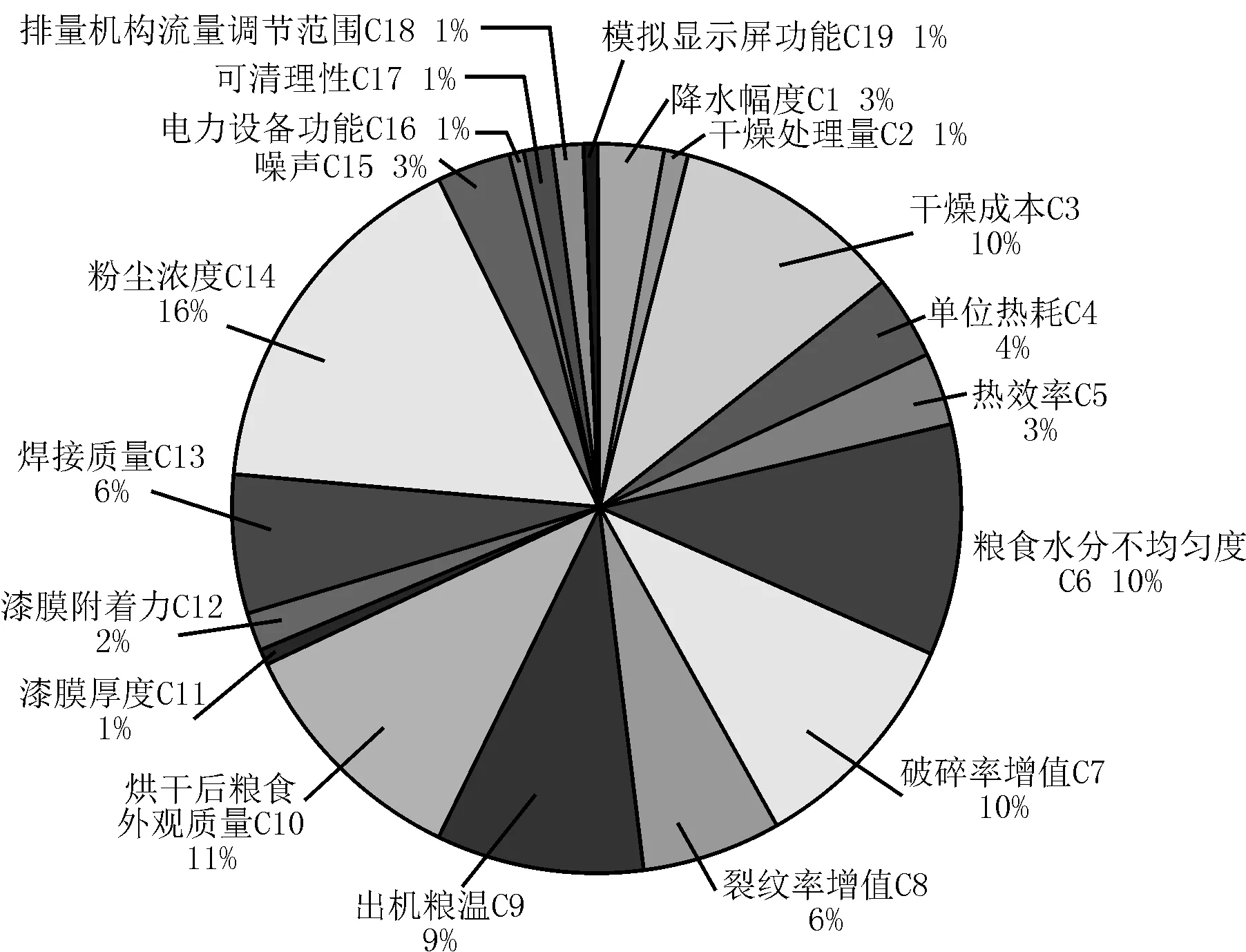
图4 准则层C层的19项细分指标的层次总排序权值
2.5 结果分析
通过对排序计算结果的分析,得出最终评价结果。
从措施层D层总排序结果看,进行综合性能评价的连续式干燥机D2的权重为0.54,大于综合性能处于平均水平的连续式干燥机D1的权重0.46,因此,可量化地证明新研发的连续式干燥机D2的综合性能比处于平均水平的烘干设备先进,从而量化地评价新研发的设备。
3 结语
本文运用层次分析法进行粮食烘干设备的综合评价,确定综合评价中各指标的权重参数,将定性的复杂问题进行定量分析,达到理想的一致性判断结果,为后续的相关研究提供一种方法及思路,推动层次分析法在粮食科研领域的广泛应用,使层次分析法成为粮食科研领域的有利科学研究手段。

