硬币“跳舞”的动力学分析

胡 立

(北京师范大学 物理学系，北京 100875)

跳舞的硬币是2018年国际青年物理学家锦标赛(IYPT2018)的一道赛题，题目翻译为：拿一个非常冷的瓶子，把一枚硬币放在瓶口.过一会儿你会听到声音，并看到硬币运动.本文要解释这个现象，并探究相关参数是如何影响硬币“舞蹈”的.

到目前为止，已有不少论文从热力学的角度对该题进行了分析[1,2].认为硬币“跳舞”是因为瓶内冷空气被外界环境加热，气体温度升高过程中压强也升高，到一定程度可以使硬币一端翘起，同时还研究了硬币“跳舞”的周期性.然而，鲜有研究者从动力学角度入手，针对单次跳动过程中硬币的运动状态进行讨论.

基于力学常识，我们可以先对硬币跳动的过程做一定性分析.硬币有一条旋转对称的轴线，圆环状的瓶口也有一条旋转对称的轴线，倘若我们将硬币放置在瓶口时两者的中心轴线是重合的，在瓶内气压升高推动硬币向上运动的过程中硬币应该是被整个抬起.然而，实验中观察到的硬币跳动过程却都是一端翘起，绕着过硬币另一端的水平轴作定轴转动.这是因为我们在放置硬币的过程中并不能保证硬币和瓶口两者轴线完全重合，总会有一个放置误差Δx，导致在瓶内气压升高时硬币更倾向于绕着远离瓶口中心的一端作定轴转动.

本文尝试从硬币的放置误差入手，对硬币单次“跳舞”过程进行分析，并就放置误差对硬币翘起高度的影响做进一步探讨.

1 理论模型与硬币的运动方程

如图1所示，我们可以构建这样一个模型：设瓶口内径为2r，一元硬币的半径为R，过程中硬币翘起的角度为θ，硬币的质量为m，水的表面张力系数为σ.

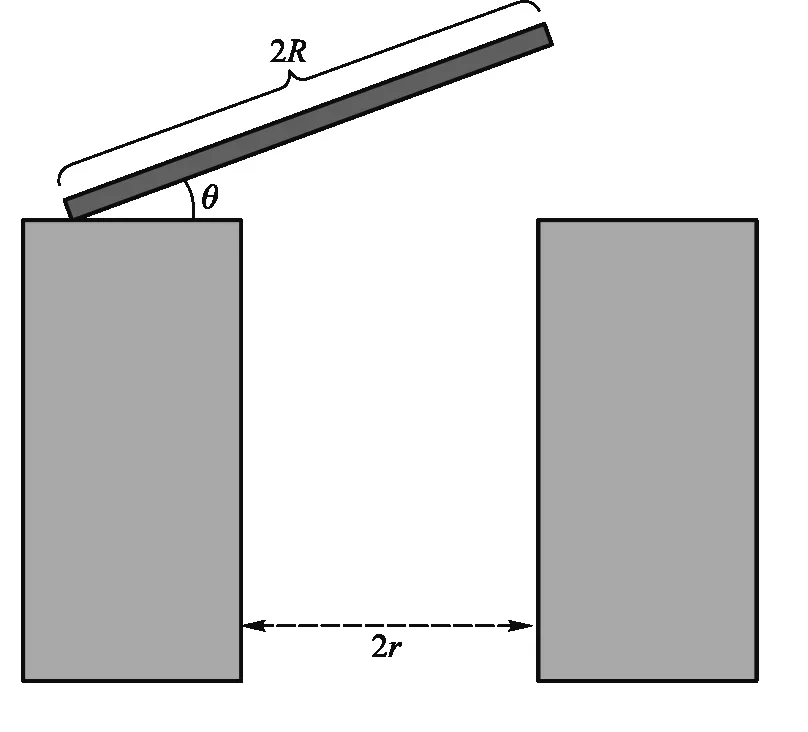
图1 硬币“跳舞”的示意图

初始时刻，硬币水平地静止在瓶口，其边缘与瓶口接触区域有一层薄薄的液膜，随后在内部气压的作用下，硬币更靠近瓶口中心的一端迅速向上翘起，翘起至特定高度时，硬币与瓶口间的液膜破裂，瓶内外气体快速交换(此过程可视为绝热膨胀)[2]，瓶内压强降低，导致硬币受到的向上的支持力减小，硬币转动的角加速度方向变为液膜破裂前的相反方向.

硬币在液膜破裂前的转动过程中受到3个力提供力矩：竖直向下的重力、垂直于硬币表面向上的支持力以及垂直于硬币表面向下的表面张力[3].由于放置误差的存在，硬币受到的向上的支持力对应的力臂是(R+Δx)，硬币的运动方程为

(1)

式中I表示硬币绕轴转动的转动惯量，p1表示液膜破裂前硬币翘起的短时间内瓶内外气体压差.由于硬币可近似为薄圆盘，故其绕轴转动惯量为[3]

(2)

在液膜破裂后的转动过程中，硬币的运动方程为

(3)

式中p2表示液膜破裂，内外气体交换后的短时间内瓶内外气体压差(后续实验表明p2≠0).硬币翘起高度可表示为H=2Rsinθ.

2 实验装置与方法

图2是主要的实验装置示意图.其中有采用亚克力材料自行制作的瓶子，并在其内部插入采样率为2 Hz、分辨率为0.1 Pa的压强传感器(插入压强传感器是为了探测硬币“跳舞”过程中瓶内压强的变化，尤其是瓶内外气体交换前后的压强，为数值计算提供必要参数).

实验时，将冷却后的瓶子连同压力传感器置于温度均匀的室内桌面上，按一定的放置误差Δx放置好硬币，并采用高速摄像机对硬币运动过程进行录制.

图2 实验装置示意图

实验装置的参数为：R=12.5 mm,r=10.00 mm,m=6.05 g,水的表面张力系数σ≈72×10-3N/m.

实验主要分为两部分，一是记录硬币翘起高度随时间的变化，二是测量瓶内的压强变化，特别是硬币运动过程中的压强变化.因为液膜破裂后瓶内外气体交换十分迅速，我们可以将液膜破裂前硬币上升过程中瓶内外压差p1视为常量，液膜破裂后短暂时间内瓶内外压差p2视为常量.

由图3可以发现，内外气体交换后瓶内外压差并不为零，这与一般文章所认为的“绝热膨胀后内外等压”并不相符.另外，由于压强传感器采样率为2 Hz的限制，我们并不能测量出硬币舞动过程中微小时间段内瓶内外压差变化的确切数值，但可以选取多次测量的极值分别作为p1和p2.显然，测量次数越多，所得极值越逼近真实值.经过多次测量，最终测得p1=196 Pa，p2=61 Pa.

图3 硬币连续跳动时瓶内外压差p与时间t的关系曲线

同时，多次实验可以发现，在不同的放置误差下，硬币翘起过程中液膜总是在同一高度H0=0.82 mm破裂，这也将成为数值计算时液膜破裂时间的重要判断依据.

3 结果与分析

如图4所示，在给定放置误差Δx=0.7 mm的情况下，随着时间t的增大，硬币翘起高度H先升高后降低，且理论与实验符合得较好.

图4 硬币翘起高度H与时间t的关系曲线

同时，实验所测得的全过程时间比较短，这是因为实验过程中液膜破裂并不完全，瓶口与硬币的接触部分仍有一部分残留的液膜.倘若在理论模型中的液膜破裂后运动过程也加入部分表面张力，则理论模型的全过程时间会更接近实验测定值.

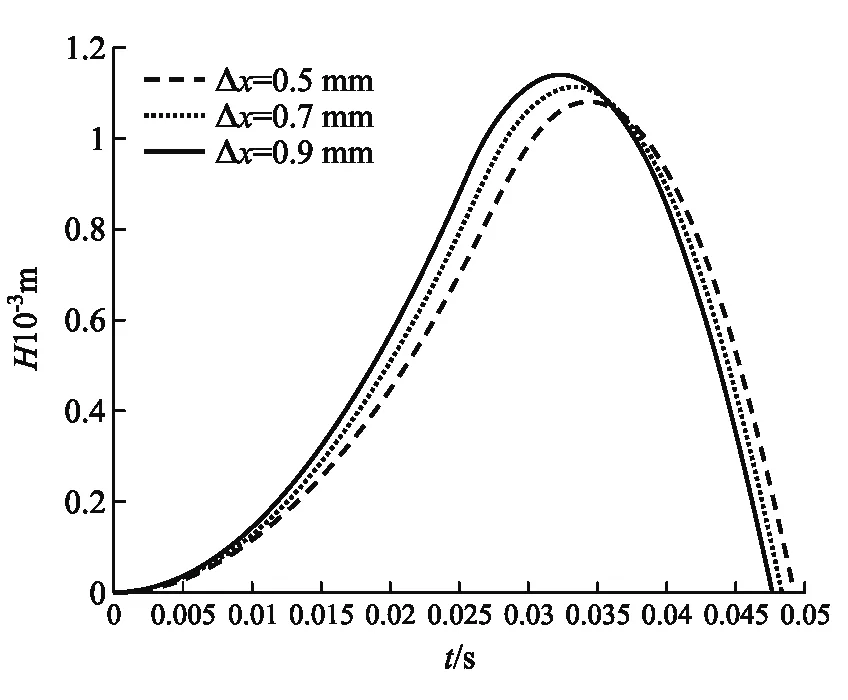
图5 等差地改变放置误差Δx时H与t的理论关系曲线

在图5中，等差地改变放置误差Δx，发现硬币所能达到的最大高度Hmax随着Δx的增大而增大.这与我们的物理直觉是相符的，放置误差越大，瓶内压强提供的向上支持力力臂(R+Δx)越大，硬币翘起的角加速度就越大，硬币更容易翘起且翘起更快，进而在液膜破裂时积累了更大的角速度，能够达到的最大高度Hmax也随之增大.

3 结论

本文通过提出“放置误差”这一重要概念，从动力学的角度，对硬币“跳舞”的过程进行了分析，推导出硬币运动的二阶常微分方程，通过数值计算发现硬币翘起的最大高度与转动全程时间都与放置误差存在密不可分的联系.放置误差越大，硬币翘起的最大高度就越大，转动全程所花的时间越少，并且通过实验验证了理论模型的正确性.