两种不同形状煤堆自燃升温特征的数值模拟

刘星魁

(河南工程学院 资源与安全工程学院，河南 郑州 451191)

煤炭自燃时常威胁煤矿正常生产。事故监测数据表明，煤炭自燃是煤矿井下重大安全事故的重要诱因之一[1]。近五年，伴随各类宏观调控政策的出台[2]，以及市场需求量的降低，煤炭销量时常波动，导致煤场会长期储存大量周转煤。出于成本限制，储煤场地多为简易半封闭式，甚至完全露天，如港口码头、郊外空地等[3]。然而，作为一种典型的多孔吸氧物质，煤在露天堆放时极易氧化，引发自燃，威胁现场作业人员的安全，造成经济损失，且燃烧时会持续释放各类碳化物造成空气污染[4]。因此，煤炭自燃预防、预警工作的重点不仅包括井下煤巷、煤柱、采空区等易自燃区域，也包括地面煤堆。

针对煤堆自燃问题，文献[5]提出的技术手段除现场即时温度数据监测外，还包括数值计算平台，通过计算机完成模型的构建、求解、分析，并结合实验对模拟结果进行验证。文献[6]指出了煤堆温度动态分布特征及其影响因素。文献[7]与文献[8]对煤堆内部漏风分布进行了分析，并模拟了多物理场耦合下煤堆的自燃过程及火点位置。文献[9]利用有限差分法对二维煤堆自燃模型进行了数值求解，分析了不同堆放方式对煤堆传热与燃烧的影响。在大量相关数值模拟应用研究中，在二维平面上，煤堆形状通常被近似为梯形或三角形[10-11]，然后分析区域内流场及温度分布信息，进而得出结论，但少有文献对比这两类形状煤堆自燃特征的不同之处。本研究通过数值模拟结合实验分析了梯形煤堆和三角形煤堆(简称三角煤堆，下同)的升温特性，对比结果不但能够指导防火工程实践，还可对数值模型进行反馈以提高模拟方法的准确性。

1 基本假设及数学模型

基本假设如下：(1)煤堆内部风压与速度的耦合符合Darcy定律；(2)将煤堆简化为二维模型，仅对某一断面内物理场分布进行分析；(3)空气中只包括氧气和氮气，暂不考虑碳化物对流场的影响；(4)煤堆内流体与固体之间可以达到热平衡；(5)煤堆结构与孔隙度保持稳定。经过上述假设，煤堆自燃可以等效为一个二维平面上具有热源的层流多孔区非稳态传热问题。

基于上述5点假设，以Darcy定律为基础，考虑空气密度随温度的变化，煤堆内部的渗流模型可以表示为

(1)

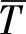
(2)

式中：ε为孔隙率；d为煤体颗粒粒径。参考大部分煤堆的典型特征，这里ε和d分别取0.3 mm和10 mm。

煤堆内部的气体扩散模型和升温模型为

(3)

(4)

式中：D为多孔介质内氧气扩散系数，m2/s；t为煤堆氧化时间，s；w为氧气质量分数；ρwhole为煤堆密度，kg/m3；r为煤堆消耗氧气能力，kg/(m3·s)，q为放热强度，W/m3，r和q是煤自身的物质参数[12]，必须根据实验确定；cair和ccoal分别对应空气与煤堆的热容，J/(kg·K)；λair和λcoal分别为空气与煤颗粒的导热系数，W/(m·K)；cwhole和λwhole分别为煤堆的热容与导热系数：

cwhole=εcair+(1-ε)ccoal，

(5a)

λwhole=ελair+(1-ε)λcoal。

(5b)

2 物理模型及计算结果

2.1 物理模型概括

煤场中小型煤堆占地面积通常在10 m2左右，高度为2～5 m。为了便于比较，本研究将两种形状煤堆的宽度都取8 m，高度都取3 m，左侧为迎风面，右侧为背风面，如图1所示。这里认为煤堆模型下边界为地面，煤堆与地面的导热条件为

图1 两类煤堆的物理模型概括图Fig.1 Sketch maps of two kinds of coal pile physics models

λcoalΔT=qcon，

(6)

式中：qcon为煤堆向大地传递的热通量，W/m2。煤堆上边界与大气接触，此处煤堆与大气存在对流和导热，换热关系为

λcoalΔT+ρCairVT=h(T-T边界空气)，

(7)

式中：T边界空气为煤堆边界附近空气温度，K。整个环境的初始温度为300 K，风流从左至右掠过煤堆，风速恒定为3 m/s，空气缓慢渗入煤堆后会与煤逐渐发生氧化反应，释放热量，引起煤堆升温。式(1)至式(7)形成封闭的数值模型，利用流体力学计算软件Fluent求解该煤堆模型内各类“场”信息，对比两种形状煤堆升温过程中的特征和区别。

2.2 模拟结果及讨论

取第20 d为观察时间节点，图2为第20 d两类煤堆的漏风趋势分布。从图2得出：三角煤堆漏风主要集中在迎风角附近，然后向煤堆深部发展，逐渐减弱，另有少量漏风迂回后从迎风面返回，形成回流；梯形煤堆漏风较均匀，风流更均匀地从迎风面渗入后分为两股，下半部渗入的漏风向背风面发展，上半部渗入的漏风向上从顶部流出。两类煤堆的区别在于：(1)三角煤堆漏风在迎风角处更加集中；(2)梯形煤堆漏风在中部和背风面附近有明显的上浮趋势。漏风趋势的不同会使自燃升温呈现不同走势。

图2 第20 d两类煤堆内漏风趋势分布Fig.2 Air leak distribution of two kinds of coal pile in 20 d

对比第20 d两类煤堆内的氧气分布情况，如图3所示。由于梯形煤堆较三角煤堆的漏风趋势更加活跃，漏风会向纵深和上部发展，所以氧气分布更加广泛，煤堆5 m处依然存在质量分数为8%的氧气，而三角煤堆氧气主要存在于迎风角2 m处，分布范围小于梯形煤堆。氧气是煤堆自燃的物质基础，可以预见梯形煤堆氧气环境更有利于自燃，升温速率和高温面积均大于三角煤堆。

图3 第20 d两类煤堆内氧气质量分数分布Fig.3 Oxygen distribution of two kinds of coal pile in 20 d

为了验证以上推论，利用非稳态模拟计算两类煤堆的升温过程，其中第20 d的温度模拟结果如图4所示。梯形煤堆第20 d的最高温度达到341 K，而且325 K以上的高温面积几乎占煤堆面积的一半，而三角煤堆最高温度仅为332 K，且325 K以上的面积只集中在迎风角附近的较小区域。两类煤堆温度分布的相同之处在于高温区的分布，迎风面附近散热速度快，温度较低，背风面附近氧气质量分数低，无法支持自燃，深入迎风面2 m左右的中部，散热减弱，氧气质量分数高，在自燃初期会形成高温区；不同之处在于梯形煤堆升温速度快于三角煤堆，高温范围更大。

图4 第20 d两类煤堆内温度分布Fig.4 Temperature distribution of two kinds of coal pile in 20 d

进一步将两类煤堆的升温过程进行对比，如图5所示。两类煤堆的最高温度在初期非常接近，但大约6 d后开始出现明显差距。随着升温速度的加快，这种差距逐渐加大，20 d内梯形煤堆升温幅度比三角煤堆高10 K。造成这种差距的原因首先在于两类煤堆漏风趋势不同，梯形煤堆漏风活跃，漏风范围广泛；其次相同尺寸下三角煤堆蓄煤量更小，单位时间内氧化反应释放的总热量低于梯形煤堆，对散热要求更低。显然，结合图4和 图5，相同尺寸下三角煤堆更有利于预防自燃，但三角煤堆占地成本更高，故管理人员需要根据安全和成本选择堆放方式。提高三角煤堆高度可降低占地成本，但煤堆倾角增加、蓄煤量加大，不利于自燃的预防。如果将三角煤堆高度增至5 m(见图6)，与图4对比，相同时间内最高温度可达338 K，接近梯形煤堆。

图5 两类煤堆20 d内升温幅度比较 Fig.5 Heating up comparison of two kinds of coal pile in 20 d

图6 5 m高三角煤堆第20 d的温度分布Fig.6 Temperature distribution of 5 m high triangle coal piles

2.3 实验验证

为了验证上述结果，在露天空场堆放梯形和三角两座煤堆，规模与上述计算模型类似。利用探杆深入煤堆迎风面2 m处，进行一个月的连续温度追踪实验，对比结果见图7。从图7看出，两类煤堆的初期温度极为接近，但12 d后开始出现差距，梯形煤堆升温幅度明显高于三角煤堆。因此，利用数值模拟或实验验证煤堆自燃现象时，应慎重考虑煤堆形状。

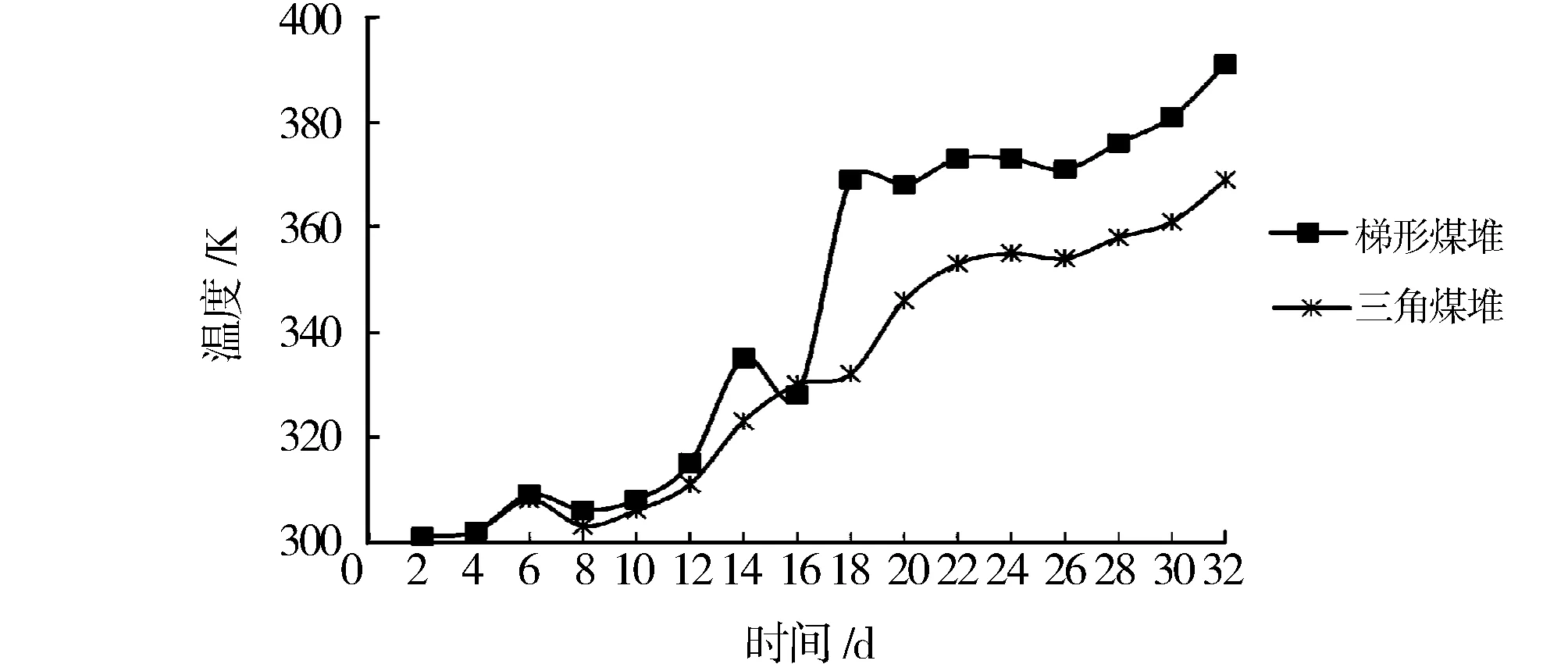
图7 两类煤堆温度实验结果对比Fig.7 Heating up comparison of two kinds of coal pile in experiment

3 结论

(1)梯形煤堆漏风趋势较三角煤堆更为活跃，漏风渗透范围广泛，易在煤堆内部形成大面积氧气富集区，加之蓄煤量大，使得梯形煤堆自燃升温幅度高于三角煤堆。

(2)温度模拟结果显示，梯形煤堆高温面积较大，而三角煤堆高温面积仅集中在迎风角附近。较小的高温面积意味着较低的自燃概率，有利于防火工作的开展。

(3)两类煤堆占地成本和自燃风险存在差异，管理人员应在成本和安全两方面进行平衡。无论是数值模拟还是实验验证均显示两类煤堆升温过程存在差异，针对煤堆自燃现象展开研究时应慎重选择煤堆模型。