数字指示称检定结果中存在的不确定度分析

宋陵英

（晋城市综合检验检测中心，山西晋城 048000）

贸易活动的开展离不开计量器具，即度量衡，它是商品交易的重要依据之一。我国度量衡发展由来已久，秦朝制定了统一的度量衡标准，宋朝形成了40 mg 精准度的戥秤，显示了当时衡器技术的发展已经较为成熟。现代社会中度量衡技术的发展逐渐进步，对贸易结算的要求逐渐提升，已经形成了较为系统的度量衡发展体系，出现了数字指示称，广泛应用于多个领域。但是在使用过程中，需将数字指示称误差控制在一定范围内。

1 数字指示称不确定度分析概述

1.1 测量依据

数字指示称不确定度测量的判断标准主要为JJG 539-2016《数字指示秤检定规程》等相关规定[1]。

1.2 被测对象

测量工作开展过程中，要求对测量对象进行相关处理，设置适宜的测量温度，对测量作业进行相应处理，由此提升测量结果的精准性。在环境温度为28.4℃，湿度为47%的条件下，用标准器为M1等级标准砝码（0～2）kg，对检定分度值为e=1 g，最大秤量2 kg，最小秤量20 g 的（Ⅲ）数字指示秤进行检定，对其最大秤量2 kg 点测量十次[2]，得到数据如表1 所示。

表1 数字指示称多次测量结果分析（单位：g）

被校对象为Ⅲ级及以下数字指示秤，如表2 所示。

表2 被校测数字指示秤的分类

1.3 测量方法及主要设备

在数字指示称运行过程中，要求对此选定相应的测量设备，并对设备运行采用相应的操作方法，在精准的测量方式之下进行作业，以此全面判定各项检测结果的准确性与否。在数字指示秤校准时，采用标准砝码加载在数字指示秤上，读取显示器数值，其与标准砝码标称值之差为其示值误差。用于校准的标准砝码为E2等级及以下标准砝码组合，规格1 mg～300 kg[3]。

表3 测量设备

2 构建数学模型

校准测量模型表示为：

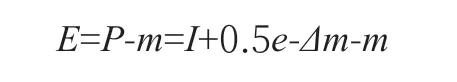
式中：E为整前示值误差；I为数字指示秤示值；e为检定分度值；P为化整前的示值；m为标准砝码质量值；Δm为附加砝码质量。输入量I、Δm、m属于相关的量，标准不确定度计算公式为[4]：

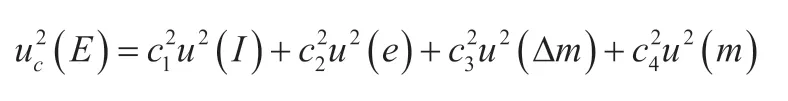
3 标准不确定度评定

3.1 重复测量u1(I)

分析标准砝码的不确定度u(m)，5 kg 载荷点开展3 次独立重复性观测，数字指示秤的重复性误差为0.7 g，3 次对应的dn值为1.69[7]，则：

据贝塞尔公式得出单次测量标准差为：

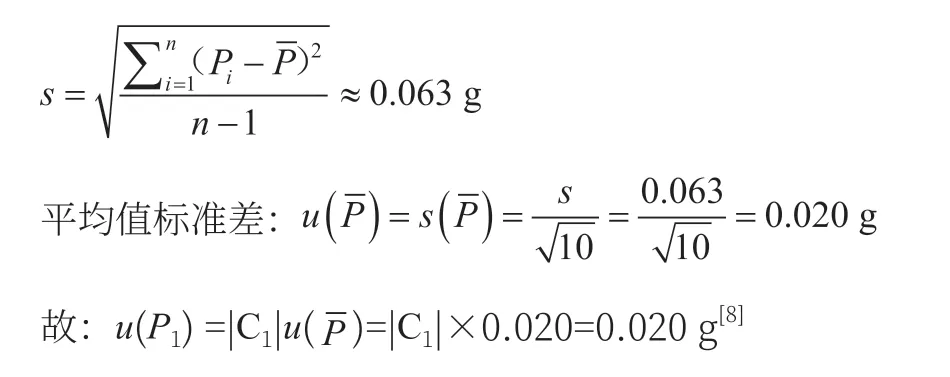
3.2 由于电源电压稳定度出现的不确定度u(P2)

电子指示称自身运行不稳定影响测量结果的精准性，可能导致最终测量结果出现变化。具体表示为：±0.2e（e=1 g），即±0.2 g。区间半宽a=0.2，其服从均匀分布，包含因子，有。

3.3 偏载不确定度u2(I)

偏载误差D为1 g 的数字指示秤，得出的数值为d1/d2，在该式中，称盘中心与砝码中心之间距离以d1表示，称盘中心与一个角之间距离以d2表示，计算中可以把d1/d2表示为1/10，由此可以得出区间半宽度表示为，这一分析结果符合服从均匀分布，由此由于偏载而出现的不确定度表示为[10]：

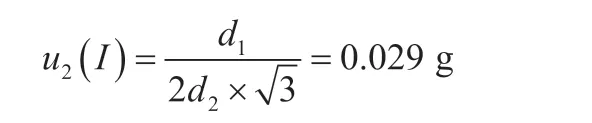
此数值整体较小，在测量计算过程中可以忽略不计，因此针对2 kg 数字指示偏载测量计算过程中，标准砝码数值为1/3max，±1.0e=1 g 即为不同承重点中最大数值与最小数值之间的差值，此项计算过程中，区间半宽服从均匀分布特征，具体包括因子。

3.4 分辨力不确定度u(e)

检定分度值e的数字式衡量仪器，区间半宽度0.5e，服从均匀分布，不确定度表示为[11]：

3.5 附加小砝码不确定度u(Δm)

附加小砝码为F1等级100 mg 砝码，共7 个，100 mg 的F1等级标准砝码允差0.05 mg[12]，得出：

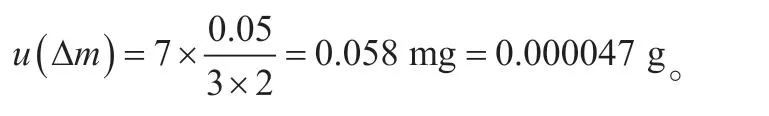
该分量很小，忽略不计。

3.6 标准砝码的不确定度u(m)

若测量作业中标准砝码选用不当，则可能影响测量结果，对此进行相应分析。结合JJG 99-2006《砝码》中的相关规定，针对2 kg 砝码可以出现±150 mg 误差，在区间范围表示层面，半宽a=150 mg，即0.15 g。这符合服从均匀分布特征，其中具有因子，进行数值计算，能够得出：

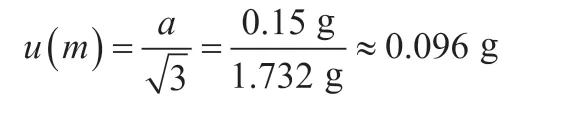
由于采用砝码的标称值，可得出：

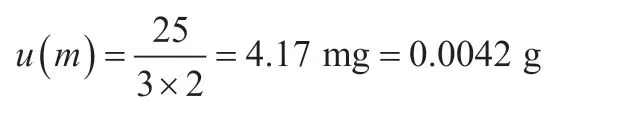
4 结束语

本文研究数字指示称不确定度检定中的正确检定方法，针对检定结果构建数学模型，要求分析不确定度出现的原因，对此进行逐一分析，并消除不确定的相关影响因素，提升测量结果的精准性，促进数字指示秤在贸易中作用的发挥，维护贸易秩序。