基于粒子群算法的永磁同步电机自抗扰控制

刘晓悦，陈瑞，白尚维

(华北理工大学 电气工程学院，河北 唐山 063210)

永磁同步电机(Permanent magnet synchronous-motor, PMSM)由于具有性能优越、效率高且结构简单等优点，被广泛地应用在工业、交通、军事等领域[1]。但实际的工作中，永磁同步电机也存在着强耦合、参数易变、非线性和负载对象复杂多变等诸多问题[2]。这些因素影响着PMSM的控制性能。如今的永磁同步电机多采用的是经典的PID三环控制，此种控制方法较为简单，易于实现，但由于其线性的结构，导致PID控制适用性较差，且系统的抗干扰能力不足。

为了提高永磁同步电机控制系统的性能，研究者提出众多的控制方法。自抗扰技术不受被控对象内部机理和外来扰动的影响[3]。它由跟踪微分器、扩张观测器和非线性状态误差反馈三部分构成[4]。作为ADRC的关键组成，扩张观测器能将系统内部的扰动视为总扰动，然后对扰动进行实时的估计并补偿，由此提高了系统的抗扰动能力。同时，跟踪微分器和非线性状态误差反馈控制器的存在，保证了系统能快速无超调地跟踪输入信号。但是ADRC有着较多的控制参数需要调节，而且调节过程复杂繁琐，这是自抗扰控制技术一直存在的问题[5]。

该项目提出了一种改进的永磁同步电机自抗扰控制系统。首先，在矢量控制和PID控制的基础上，系统摒弃了传统的三环控制结构，取而代之的是结构简单的双环控制结构。同时设计了二阶自抗扰控制器，代替了矢量控制中的位置和速度环，建立了永磁同步电机位置伺服系统。然后，为了解决参数整定的问题，引入了粒子群算法，对扩张观测器的3个重要控制参数进行正定优化[6]。实验结果表明，此方法较好地提高了PMSM的控制性能。

1 PMSM数学模型

在d-q旋转坐标系下，假设永磁同步电机磁场在空间中呈正弦分布，忽略磁路饱和、磁滞和涡流损耗带来的影响[7]，当采用矢量控制时，PMSM的数学模型为

电压方程：

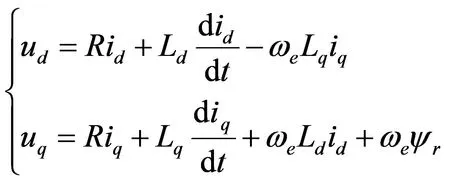
(1)

运动方程：

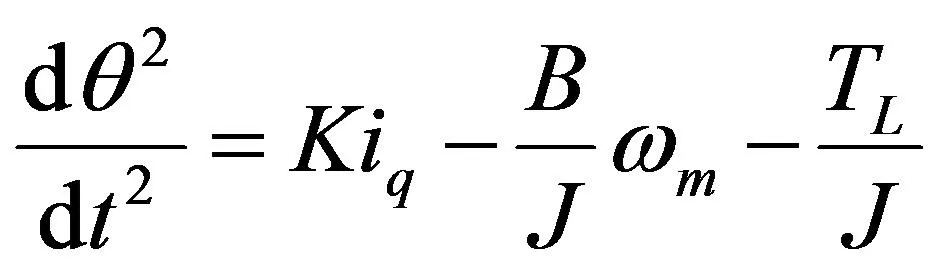
(2)

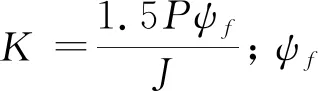
2 PMSM的ADRC位置控制器设计

自抗扰控制器由三部分组成，分别为跟踪微分器(TD)、扩张状态观测器(ESO)和非线性状态误差反馈(NLSEF)[8]，二阶自抗扰控制器结构图如图1所示。

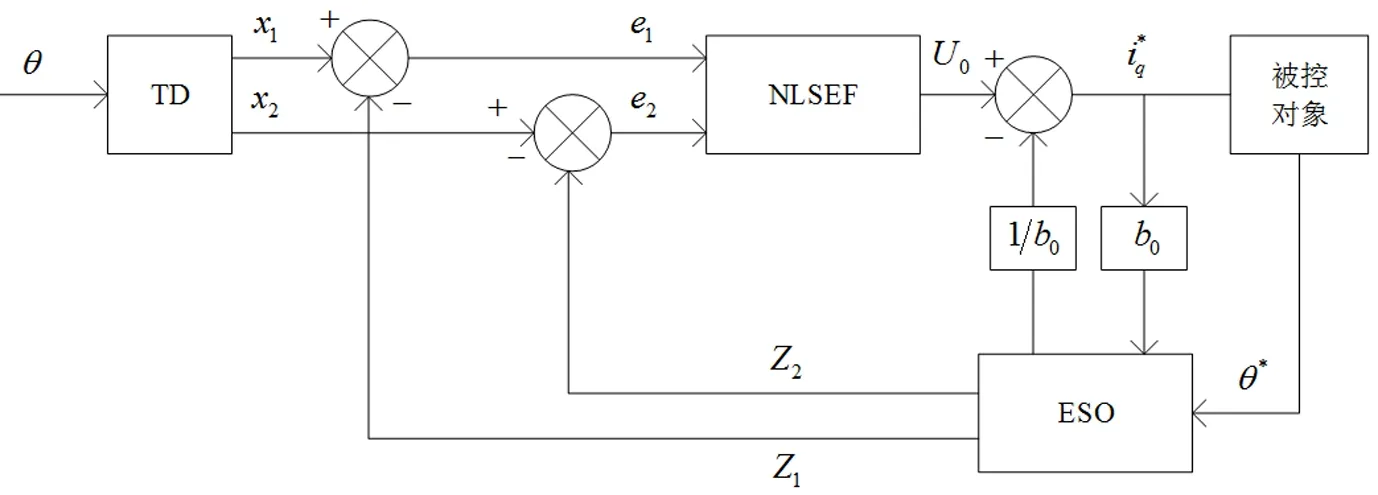
图1 二阶自抗扰控制器结构框图

跟踪微分器(TD)作为ADRC的重要组成部分，主要作用是提取连续信号和微分信号，并对信号进行跟踪，从而保证系统无超调现象[9]。而且跟踪微分器能抑制信号突变带来的扰动。

跟踪微分器的形式：

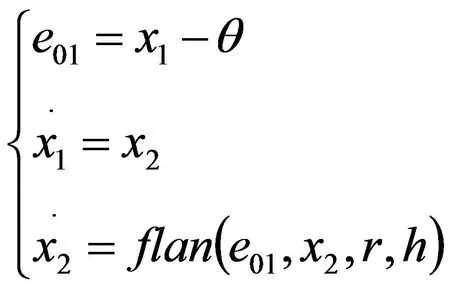
(3)

式中，θ是给定转子位置；x1是θ的跟踪信号；x2是θ的微分信号；γ为速度因子，确定跟踪速度；h为滤波因子，确定滤波数量；函数fhan如下：

(4)

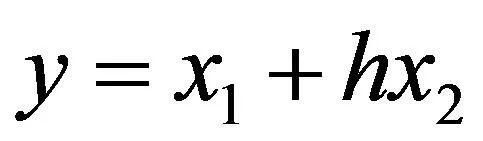
扩张状态观测器方程为：

(5)

非线性误差反馈控制器:

(6)

其中α1，α2，α3，α4，α5为最优控制函数的非线性因子；δ1，δ2为滤波因子；β1，β2为可调参数。

基于矢量控制的PMSM二阶自抗扰位置控制器系统结构框图如图2所示。控制系统的整体控制结构采用的是ADRC位置控制外环与PID控制的电流内环相结合控制方法。此控制结构简单，能够保证电流环的快速响应[11]。

图2 ADRC位置控制系统器结构框图

3基于粒子群算法的ADRC参数优化

粒子群算法(Particle Swarm Optimization,POS)的理论依据就是参考了鸟群在不确定空间内搜寻食物的过程[12-14]。它是一种智能的优化算法，很多参数寻优事例都用到了此种算法。该项研究将对扩张状态观测器(ESO)的控制参数β01、β02、β03进行优化。将ESO的3个控制参数定义为PSO的一个粒子。每个粒子和粒子群如下：

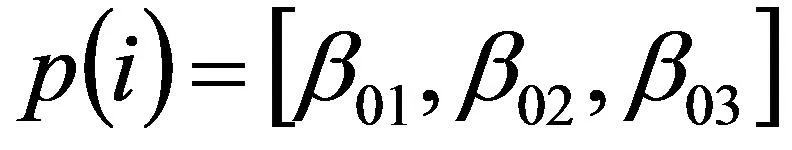
(7)

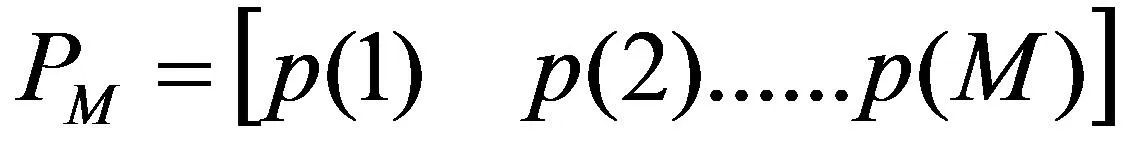
(8)

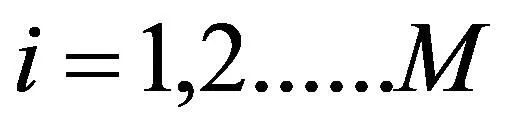
式中，M为粒子群总数。粒子在运行中，会依照最佳位置Pbest和全局极值gbest不断地变化调整，然后得出最优解。速度与位置更新公式如下：

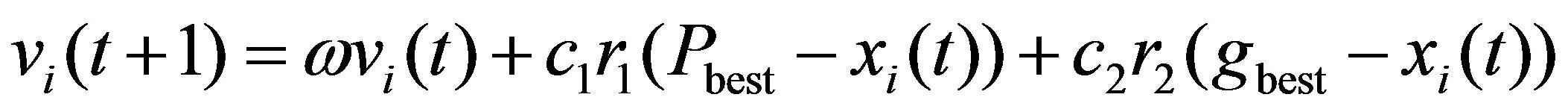
(9)

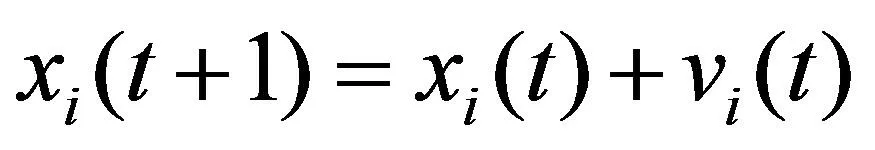
(10)

式中，vi(t)为粒子当前的速度；vi(t+1)为更新的粒子速度；xi(t)为当前粒子位置；xi(t+1)为最新粒子位置；ω为惯性权重，用来权衡局部最优和全局最优；γ1，γ2为0到1的随机数字；c1为局部学习因子；c2为全局学习因子。

粒子群中每个粒子的适应度值是由适应度函数确定的[15]。所以为了避免超调，寻找控制器与粒子最优位置之间的联系，把适应度函数定义为：

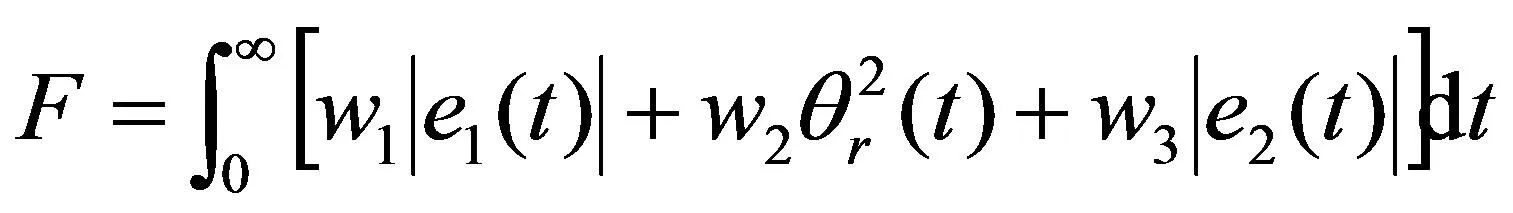
(11)

式中，e1、e2为瞬时误差；ω1、ω2、ω3为权重，ω3≫ω1通常情况下，ω1=0.999，ω2=0.001，ω3=100。

自抗扰控制器有着众多的参数，而其中ESO的3个控制参数β01、β02、β03是决定控制器性能的重要参数，而且这3个参数差值较大，调节起来较为复杂，所以采用粒子群算法对ESO的3个参数进行寻优整定，基本过程如下：

(1)进行初始化，设定ESO的3个待优化参数β01、β02、β03，产生粒子群的初始位置和速度。

(2)进行个体评价，由式(11)的适应度函数求出种群中所有粒子的适应度值。

(3)得出粒子的新位置和速度。根据粒子的适应度与粒子群个体最优解Pbest和全局最优解gbest进行比较，得到粒子的最新速度与位置。

(4)求得最优解，当满足条件时，输出全局的最优解β01、β02、β03，并带入到ESO中，若不满足条件则转至(2)。优化后的自抗扰控制器结构如图3所示。

图3 优化的自抗扰控制器

4仿真结果

永磁同步电机的参数和负载受外界环境的因素影响很大，会随着环境的变化而改变。因此,仿真主要研究永磁同步电机控制系统在不同的负载和参数下，系统的控制精度。首先在Matlab/Simulink中搭建仿真模型，然后在不同的输入信号和干扰信号的情况下得出仿真图形，通过仿真图形对比，进一步分析不同的情况下，传统的PID控制性能与优化后的ADRC控制性能。选择合适的PMSM电机，仿真中所应用的PMSM参数如下表1所示。

表1 电机参数

ADRC的部分参数采用粒子群算法进行寻优整定，为了验证优化后的ADRC的控制性能，仿真中比较了在相同条件下，改进的ADRC与传统PID控制的性能指标。

为了检验优化后ADRC系统在加负载后的抗干扰能力，在其他条件完全相同的情况下，给定位置信号为40°的机械角度，并在t=0.3 s时加载3.0 N·m，t=0.5 s时卸载。仿真对比了阶跃信号下，ADRC与传统的PID控制的性能指标。图4所示为优化ADRC与PID抗干扰能力对比。

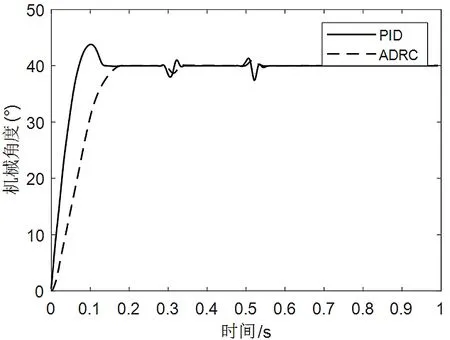
图4 优化ADRC与PID抗干扰能力对比

由图4可看出，与改进ADRC相比，PID达到稳定的时间较快，而且调节迅速。但是在启动、加载和卸载的时刻，PID控制都存在着较大的超调。反观ADRC，不仅跟踪速度快，而且启动过程不存在超调，在加载和卸载的时刻，相对传统的PID，也能较快的进行动态补偿，并且抑制扰动。验证了优化的ADRC具有更好的动态性能和稳定性。

上述仿真输入的信号为常值，下面对系统加入变化的随机负载扰动，进一步验证系统的稳定性和跟随性。

图5为加入变化的随即负载启动稳定性能对比，如图5(a)所示，加入变化的随即负载后，由于负载的变化较大，这2种控制性能都受到了一些影响。从图5(b)可以看出，ADRC的启动过程受到的影响并不大，仍然没有超调的出现，而且进入稳态的时间基本没有变化。反观PID制，不仅出现了较大的超调，且进入稳态的时间，也稍慢于ADRC控制。由此更能验证改进的ADRC具有良好的鲁棒性。

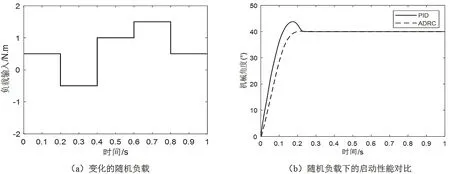
图5 随机负载下的启动稳定性能对比

上述仿真为阶跃响应对比，下面进行正弦跟踪仿真实验。设置20°的正弦波幅值，2 s为一个周期进行测试，其他控制参数不变。图6所示为正弦跟踪测试。

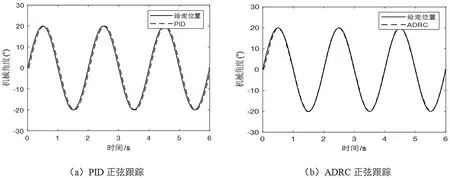
图6 正弦跟踪测试

由图6(a)可以看出，PID的跟踪曲线，较给定位置信号，出现了0.06 s的滞后，且滞后一直存在。反观图6(b)ADRC的正弦跟踪测试，前0.5 s，ADRC的正弦曲线较跟定信号，也出现了一些滞后，但是到了0.5 s，ADRC的正弦曲线完全跟上了给定信号，并一直保持了下去，可见ADRC的正弦跟踪性能更加优越。由此可得，优化的ADRC与传统的PID控制相比，具有良好的动态性能和控制精度，且更适用于高精度的控制系统。

5结论

(1)提出了一种改进的永磁同步电机位置自抗扰控制系统。在PMSM控制系统中，采用矢量控制与自抗扰控制相结合的控制策略。同时采用自抗扰位置控制器，代替了速度环和位置环，构成双环控制模式。并用粒子群算法优化自抗扰控制器的部分控制参数，使控制器进一步优化。

(2)通过仿真，对比了优化后的ADRC与传统的PID的控制性能，结果表明改进的ADRC具有良好的动态性能，响应速度快，抗干扰能力更强，更适合高精度控制系统。