基于深度神经网络的条纹结构光相位展开方法

肖昆，宋万忠

（四川大学计算机学院，成都610065）

0 引言

三维测量技术在恢复物体三维重构方面发展迅速，在机器视觉、文物保护、工业元件检测等方面得到了广泛应用。其中相位测量技术通过对被测物体表面投射编码光栅，计算条纹在物体表面上的相位高度变化，进一步映射出物体的高度信息，从而完成物体的三维重构。实际中，由于使用反正切函数得到的相位值在[－π，π）之间，需要将相位主值准确地展开为连续分布的真实值。在截断相位图噪声较小、连续、无阴影、对比度较好等理想情况时，只需要沿相位图的行与列逐点依次展开，在相位截断处加减2π的整数倍，即可获得连续相位值。然而在实际情况中，由于物体局部形状变换剧烈、图像低对比度、成像阴影或投影阴影、运动模糊、离焦等因素的存在，对于依赖路径展开的单频截断相位展开方法，容易引起相位错误沿着路径传递，导致展开结果不理想或失败。

为了解决以上问题，人们研究了不少相位展开方法，主要有时间相位展开方法和空间相位展开方法。时间相位展开方法需要多套条纹，对设备的要求也比较高，因此测量速度比较慢[1]。而空间相位展开方法只需要一套条纹图，即可进行相位展开，速度比较快，然而，由于噪声、阴影、相位不连续等不可靠区域的存在，使得沿相位路径展开的空间相位展开方法很容易造成误差传递。传统的空间相位展开方法可分为可靠度引导算法[2]、最小范数算法[3]等方法。可靠度引导算法主要思想是首先确定相位点的可靠度，并对相位点的可靠度值进行排序，然后相位展开沿着可靠度最高的方向进行展开，能够避开不可靠区域的点，使得相位展开把误差降低至最小[4]。然而如果存在不连续的情况时，质量图就不能完美的进行相位展开[5]。最小范数算法是指求出展开截断相位F 的相邻像素相位差和截断相位j 的相邻像素相位差最小LP 范数意义上的解，其中比较经典的是基于快速傅里叶变换（FFT）的最小二乘法（FFT-LS）[6]，主要思路是对截断相位进行周期延拓，通过计算得到真实的相位值。然而在展开截断相位时，需要进行周期延拓，比较占用时间，同时要进行FFT 变换，需要满足一定条件，具有局限性[7]。传统方法在某种程度上确实降低了误差，然而在低对比度、条纹断裂、图像离焦和运动模糊等干扰因素比较复杂的情况下，传统的可靠度引导算法、最小范数算法等在进行截断相位展开时，仍然面临很大的挑战。

近年来，随着深度学习与卷积神经网络的融合发展，尤其是2012 年多伦多大学的Alex Krizhevsky 等人[8]提出的AlexNet 模型，使得深度卷积神经网络得到了快速发展，一些科技上棘手的问题得到了很好地解决，例如在语义分割、语音识别、人脸识别等方面。深度卷积神经网络（DCNN）是一种模拟人脑的行为特征，包含许多隐藏层的神经网络。深度学习是一种基于数据进行学习的方法，使得计算机或机器通过训练得到多层的深度卷积神经网络，建立图像特征与语义之间的对应关系[9]。

基于以上问题，本文提出了一种采用深度卷积神经网络的空间相位展开新方法，截断相位图的展开被分为不可靠区域检测和可靠区域展开两个子问题，深度卷积神经网络被用于检测截断相位图中的低对比度、条纹断裂、图像离焦和运动模糊等不可靠区域，可靠区域的相位展开用传统算法完成。为训练能处理高分辨率截断相位图的神经网络，本文提出了位移采样方法。本文通过采用真实牙模三维扫描数据对神经网络进行训练，并与使用传统空间相位展开算法对相位进行展开的对比实验，得到了有效真实的结果，验证了本算法的有效性。

1 本文方法

1.1 DCNN网络模型

深度卷积神经网络是一种比较复杂的网络结构模型，主要是通过增加网络的深度，以达到拥有更加强大的特征学习能力和特征表达能力。然而随着深度的增加，神经网络会变得很复杂，系统参数也会越来越多，进而使得数据训练变得相当困难，最终导致梯度弥散问题[10]。本文的网络结构使用深度残差网络（ResNet）来解决这一问题，通过在卷积层加入越层的快捷链接方法有效的解决梯度弥散问题[11]。

残差块结构图如图1 所示，其中残差块的输入为x，原始映射函数（即期望输出函数）为H（x），定义残差函数为F（x）=H（x）-x，由图1 可以得出，残差块通过快捷链接的方式，直接将输入x作为输出结果与F（x）相加得到H（x），即H（x）=F（x）+x，如果F（x）=0，则H（x）=x，即为图中的恒等映射。所以对于残差网络，当下层网络中存在误差时，只要网络训练能够使得残差函数F（x）逼近为0，也就是通过快捷链接转变为恒等映射，使得输入x近似于输出H（x），就能够降低由于网络层数太多带来的梯度弥散问题。

图1 残差块结构

本文采用深度卷积神经网络进行截断相位图的不可靠区域检测，网络结构如图2 所示。网络模型来自于Fastai[12]的U-Net[13]实现，U-Net 是一个对称的网络结构，先经过左边为Encoder 的网络结构，使得模型能够对不可靠区域进行学习、识别等，但是却丢失了位置信息，本文Encoder 部分采用的是ResNet18 网络结构，参数如表1 所示，然后再经过Decoder 部分，使得模型结合Encoder 加深对图像不可靠区域的理解，并且重新得到了位置信息，实现了对图像的语义分割，最终将截断相位图中不可靠区域检测出来。

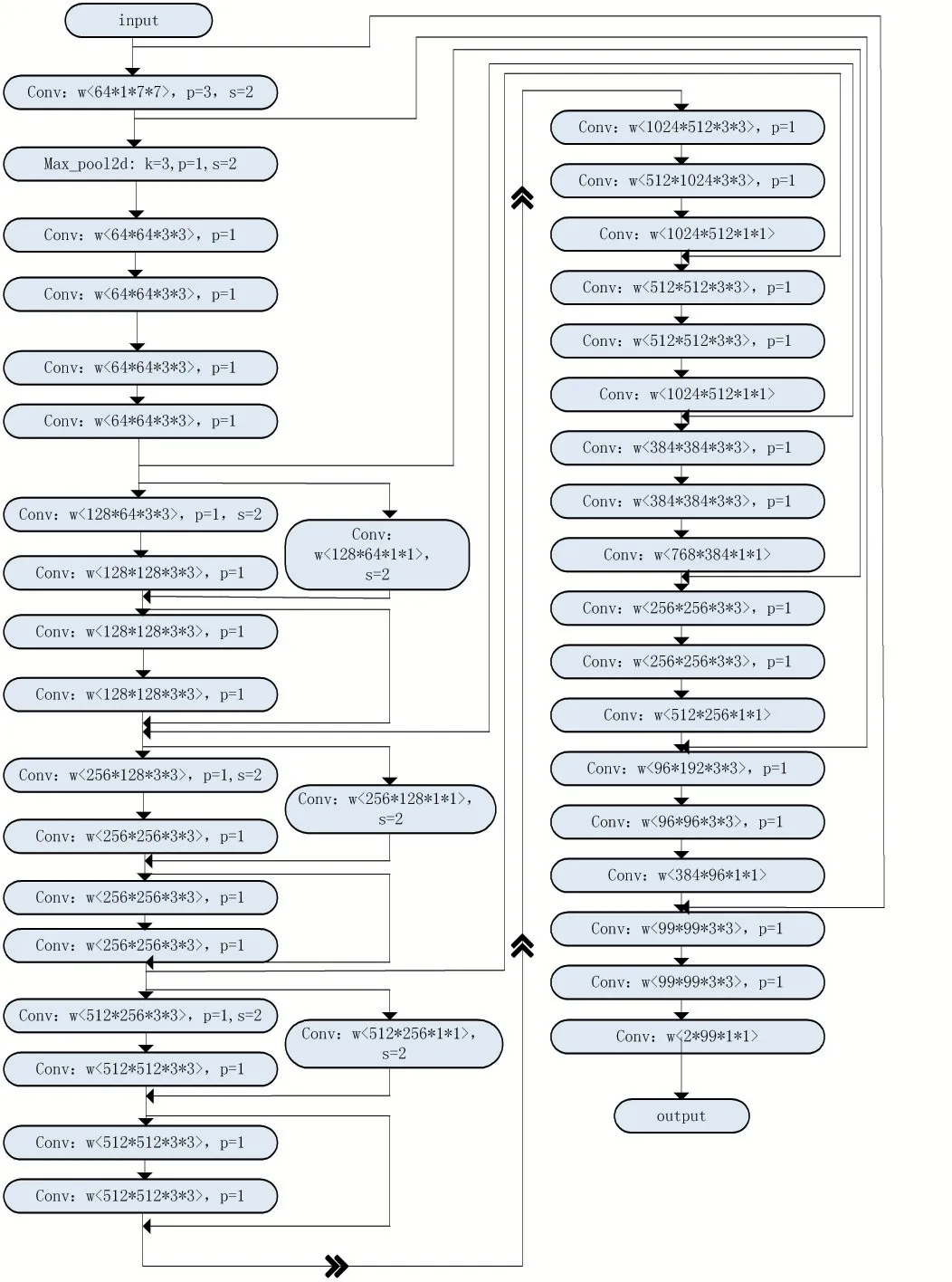
图2 网络结构示意

表1 不同深度ResNet 的网络结构

本文深度卷积神经网络中使用的损失函数为交叉熵函数，公式（1）中H（p，q）表示交叉熵，其中p（x）为真实概率分布，q（x）为预测概率分布。H（p，q）值越小表示网络预测的结果越好，所以使用交叉熵损失函数来进行损失计算。

数据输入统一固定大小为256×256，第一层为卷积层，使用64 个大小为7×7 的卷积核，填充padding=3，步长stride=2，对输入图像进行卷积运算。下一步是对卷积运算后的结果进行批规范化，作用是为提高学习速率，防止速率衰减。再经过Max 池化层，卷积核为3×3，填充padding=1，步长stride=2，进行下采样降维，最终经过网络后输出相位图中不可靠区域检测图像。

1.2 训练数据集准备

本文采用定制开发的手持式条纹结构光三维成像设备对13 个石膏半口牙齿模型进行扫描，得到了7402组数据。每组数据包括平均灰度图、截断相位图、深度图，数据点数均为1024×1024。该设备投影多组条纹，用时间相位展开方法得到连续相位分布；再结合事先标定的相机参数计算出每帧深度图和点云，通过实时地对每帧点云进行拼接和融合后，实现对物体表面的连续扫描。针对实际应用中，条纹结构光图像普遍存在的低对比度、图像离焦、运动模糊、条纹不连续和背景物体等因素在深度图中产生的无效数据点，该设备用一系列算法检测并剔除这些无效点，实现了连续扫描深度图的拼接。如图3 所示为其中一组数据图，（a）为平均灰度图，（b）为（a）对应的截断相位图，（c）为对应的深度图，其中黑色部分为无效点，深度范围为[133.57mm，145.0mm]之间。该设备输出的深度图中，已经剔除了不可靠点，并且能满足连续的深度图拼接和点云融合需要的深度图。该深度图的无效数据点可以直接作为训练输入图像的目标图像，避免了耗时的手工图像标注。

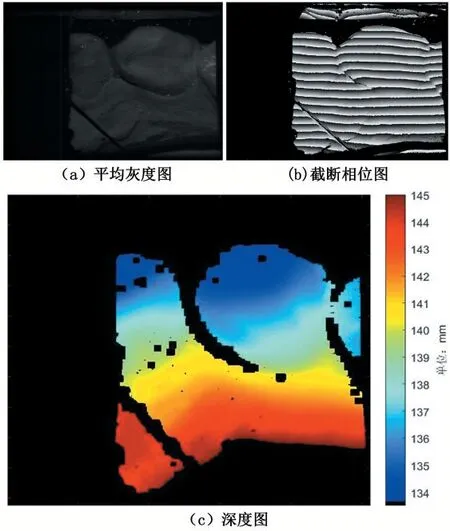
图3 牙模三维扫描数据组

由于高分辨率图像具有更多的细节信息，有助于进行截断相位图不可靠区域的检测，因此，本文将采用高分辨率真牙摸图像作为训练数据对深度卷积神经网络进行训练。

1.3 高分辨率数据集的训练方法

本文使用的数据集真实牙模图像分辨率为1024×1024 像素，然而由于现有技术（包括硬件和软件）的限制，高分辨率图像在训练网络时，无法有效地进行训练。为解决这一问题，本文提出了位移采样方法，流程如图4 所示。

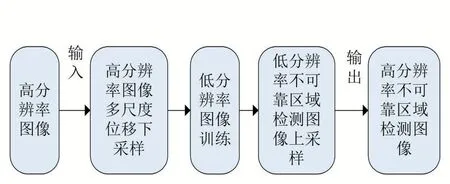
图4 位移采样流程图

方法如下：

（1）高分辨率图像多尺度位移下采样。首先预设图像分辨率，本文预设大小为256×256，采样间距计算方法为高分辨率图像与预设图像的分辨率大小相除，即1024/256=4，此处采样间距为4。根据采样间距可以得到行采样起始点和列采样起始点，然后根据行和列的采样起始点计算采样起始点为16 个，然后对高分辨图像进行16 次位移下采样，得到16 个待处理的低分辨率图像。

（2）低分辨率图像训练。预先设置每个低分辨率图像的标识信息，标识与起始点息息相关，同时得到每个像素点的坐标信息。将低分辨率图像输入到深度卷积神经网络中进行训练，得到低分辨率图像的不可靠区域检测图像。

（3）低分辨率不可靠区域检测图像位移上采样。通过对16 个低分辨率不可靠区域检测图像的采样起始点进行排序叠加的办法，得到高分辨率区域分割图，对高分辨率图像和高分辨率区域分割图进行计算可得到高分辨的不可靠区域检测图像。

通过位移采样方法能够使得深度卷积神经网络有效地处理高分辨率图像。

2 实验与分析

本文使用Fastai 在配置为Intel Core i7-9700 CPU、32G 内存、NVIDIA TITAN RTX 的计算机上对DCNN 进行训练和测试。batch size 为64，训练时间约为4 小时；测试时，一幅1024×1024 的截断相位图的处理时间约为80ms。

本实验13 个牙模扫描数据中，分别随机选出1 个牙模扫描数据作为测试数据集，2 个牙模扫描数据作为验证数据集，10 个牙模扫描数据作为训练数据集。

为验证本文方法的有效性与可行性，设计了一种对真实牙模三维扫描截断相位图进行不可靠区域检测，并与使用传统方法对原始截断相位图、去除不可靠区域的原始截断相位图进行相位展开的实验，并将两者的实验展开结果进行对比分析。

首先在进行实验之前，本文对比了每一幅牙模的平均灰度图与其截断相位图，图5 表示了含有阴影、低对比度、运动模糊、离焦等四种不可靠区域去除后的情况，其中（a）表示平均灰度图、（b）表示与（a）一一对应的原始截断相位图，（c）为用DCNN 训练后输出的二值图模板，其中不可靠区域的无效点统一设置为0，可靠区域的点设置为1。在实际情况中，这些干扰因素往往是无法避免，本文的重点将是检测并去掉截断相位图中这些不可靠区域，然后对截断相位图中剩下的可靠区域进行相位展开。

图5 去除截断相位图中不可靠区域的结果

检测结果如图5（d）所示，是参照二值图模板（c）将（b）中一一对应的原始截断相位图中的阴影、低对比度、运动模糊、离焦等不可靠区域检测去除后的结果。

本文使Herrae 算法[14]对截断相位图进行相位展开，输入数据分别为754 幅原始截断相位图像与754幅原始截断相位图去除不可靠区域后的图像，图像大小都为1024×1024。通过实验运算，图6（a）显示原始截断相位图在分别存在阴影、低对比度、运动模糊、离焦等四种情况下的相位展开结果，图6（b）为（a）中去掉不可靠区域后的截断相位图展开结果。

图6 截断相位图展开结果对比

本文采用空间相位展开方法展开得到相位图是相对相位，为更清晰地展示去除不可靠区域前后的差异，实验中将图6（a）和图6（b）中的相位图以同一像素坐标点为基准进行对齐后再进行相位展开，选出其中一列数据显示结果如图7 所示。对某列数据，除物体表面的高度跳变外，曲线应为连续平滑曲线，否则表明展开错误；这种错误在图6 中表现为图像灰度值出现跳变。图6 和图7 表明，原始截断相位图在遇到存在阴影、低对比度、运动模糊、离焦等不可靠区域时，无法有效地避开，导致展开错误沿着路径传播的情况，会出现展开效率不理想甚至失败的结果，而本文所用的方法可以有效地检测出不可靠区域，然后去除掉，对截断相位图中的可靠区域进行相位展开，效果往往比较理想。

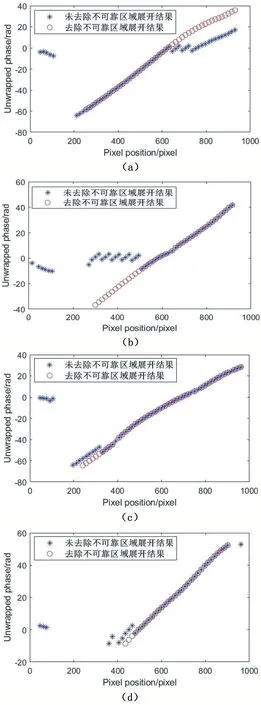
图7 去除不可靠区域前后展开结果对比图

3 结语

本文提出的基于深度神经网络的条纹结构光相位展开方法通过检测截断相位图中不可靠区域再进行相位展开，能够有效地避免错误沿路径传播的情况。然而，还有一些问题需要解决，例如本文训练需要大量数据，网络结构比较复杂，参数也比较多，下一步是减少网络参数，采用弱监督与先验知识结合的方法来减少训练数据量。