改进滑模观测器的PMSM无速度传感器控制

何世君

(黑龙江科技大学 电气与控制工程学院,黑龙江哈尔滨，150000)

0 引言

在动车、高铁和地铁等牵引控制中，学者王远东[1]发现在PMSM中速度传感器在很多条件下提供的数据精确性不高，电机操控系统开支变大，增加机身重量且很难维护等问题。因此王正等[2]提出使用无速度传感器滑模观测器的方法观测PMSM定子电压，获得电机的转速和转子位置。本文采用带饱和幂次函数的趋近律设计，在趋近律中引入饱和函数和幂次项。这样就可以有效地减小了系统输入信号的幅值，从而系统的抖振得到了有效的削弱，同时可以追踪实际转动速，使系统的可靠性大为提高。

1 PMSM的数学模型

PMSM在静止α-β坐标系当中的定子电压方程式如下：

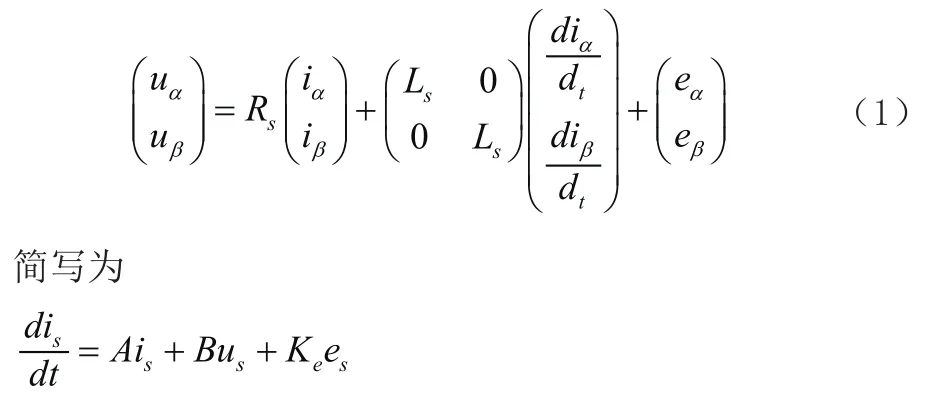
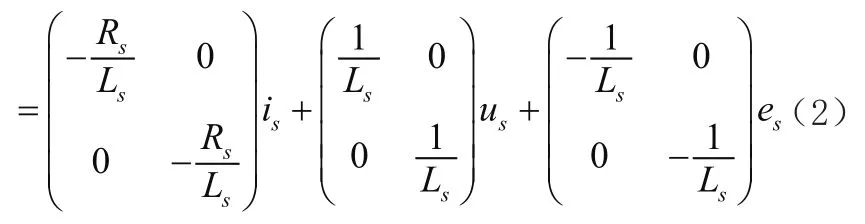
式中：uα——永磁同步电机中α坐标分量电压

uβ——永磁同步电机中β坐标分量电压

Rs——永磁同步电机中外电阻

es——永磁同步电机内部电压

2 改进滑模观测器的PMSM无速度传感器控制系统的设计

2.1 改进趋近律滑模观测器的设计

滑模变构造是指变结构操控当中的一种操控方法，是一种处理非线性体系问题的方式。

考虑到常见的情况，设计一个切换平面

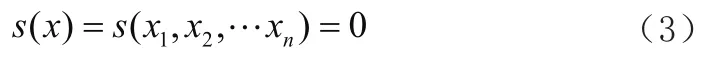
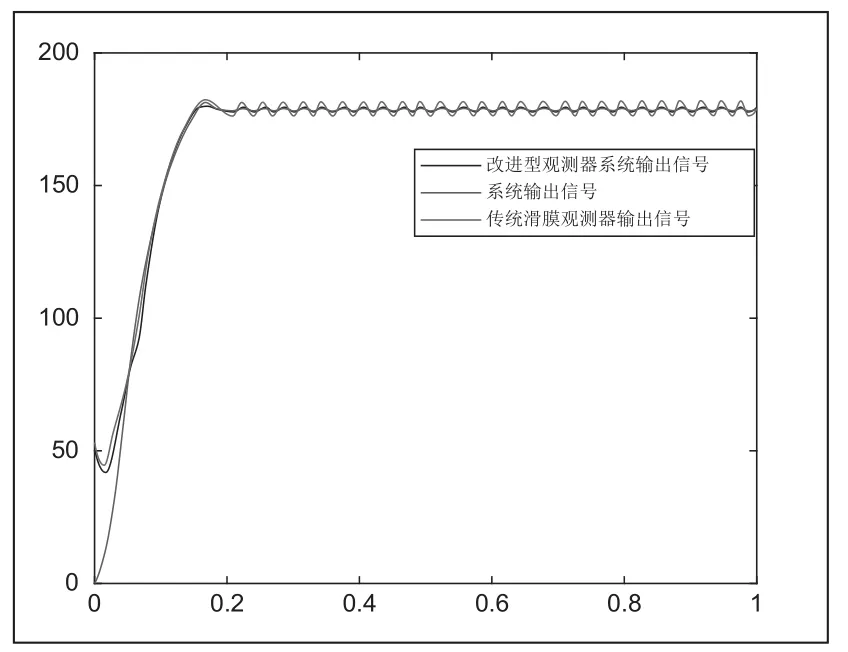
图1 两种滑模观测器作用下系统位置输出结果与观测结果

在滑模变结构当中，终止点拥有特别作用，而起始点和通常点作用不大。当运动点在切换平面上的某一个区域当中都成为终止点的时候，且一旦靠近这个区域就会在它里面移动。这时候这个区域被称为“滑动模态”区域，即“滑模”区域，系统在这个区域的移动称为“滑模运动”[3]

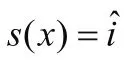
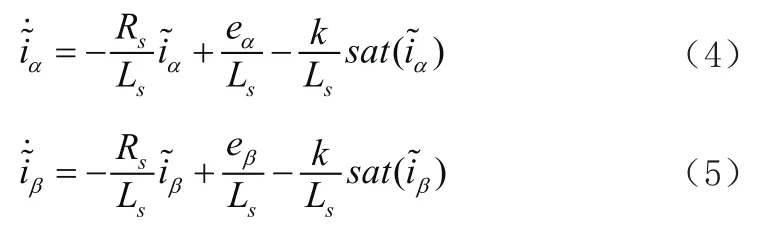
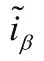
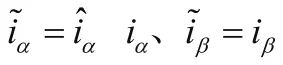
由于上面公式当中包含大量非连续的开关信号，因此使用低通滤波器把非连续的开关信号转化成相同效果的连续信号:

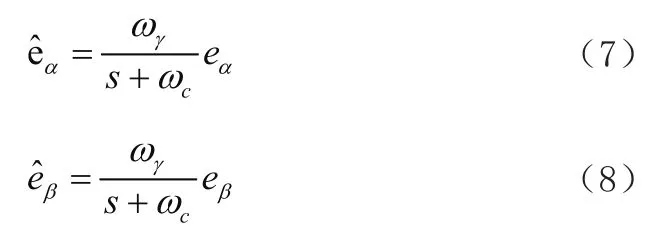
ωγ——低通滤波器角速度

传统的滑模观测器具有不连续开关特性。本文设计一种新型趋近律，在趋近律中引入饱和函数和幂次项。引入幂次项，可以通过改变幂次项的参数，改善系统的动态品质。

2.2 改进趋近律滑模观测器的仿真分析

对于传统的指数趋近律，其表达式为：

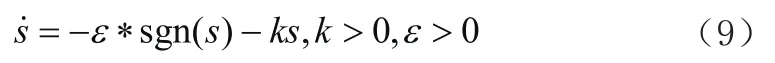
利用的是幂指数趋近律来降低抖振；所以整个系统的控制函数是：

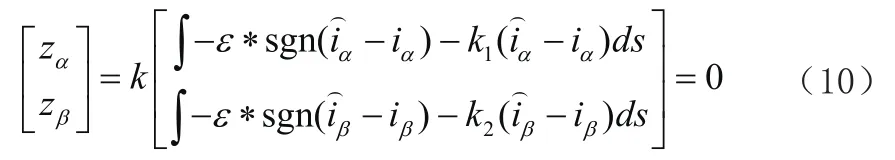
系统进入到滑模面之后，这个时候的控制量为等效控制量，因此得到如下的控制率：

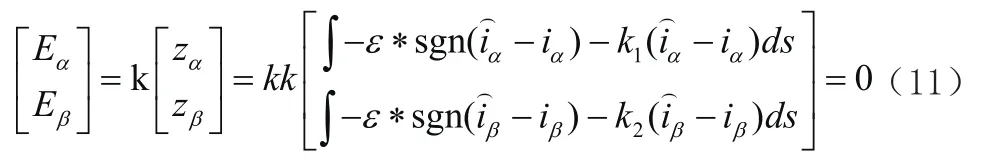
图1中，引入饱和函数和幂次项的新型滑模观测器和传统滑模观测器相比在远离滑模面的系统状态在趋近滑模面时收敛速度较小。传统滑模观测器在平衡零点附近产生抖振；改进的趋近律在一定程度上增大了收敛速度，这是由于新型趋近律具备两个可调节的幂次项系数，使系统状态在接近滑模面和远离滑模面时均具有较快的收敛速度，削弱了系统的抖振。

为了证明上面说的滑模观测器当中的PMSM无速度传感器操控系统的准确可行，使用MATLAB/Simulink仿真工具箱对体系模型进行仿真测试，转矩突然变化情况下:

下面用20r/min转动速度运行点为例子，电机从I/F开启，到操控策略转换机空载情况下，利用I/F操控方式开启，I/F设定为20r/min转动速度，交轴电流设定为1A，操作电机从停止上升到20r/min。半秒钟之后，逐渐降低交轴电流数值到0.35A。0.8秒的时候，进行操控策略更换，从I/F开启变为滑模无速度矢量操控，下面是操控当中相应的仿真波形状。

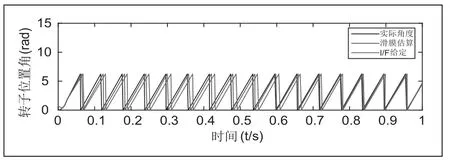
图2 转子所在地方角跟踪波形

3 结论

本文通过研究饱和函数和幂次项的新型滑模观测器的操控体系,连续获得电流估计数值与实际数值的差距不断调整模型，减少偏差，从而估计出来速度和角度数值,并对相位滞后弥补进行补偿，都可以及时精确追踪电动机的转速和角度改变，拥有操控精度高，动态特性好，鲁棒特性好等优点。